Soru Sor sayfası kullanılarak Trigonometri-1 konusu altında tanx.cotx=1, tanx=1/cotx eşitliklerini kullanma, tanjant ile kotanjantın çarpımı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
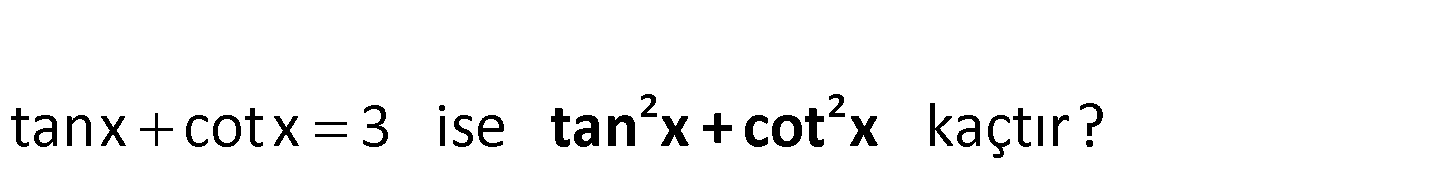

2.SORU
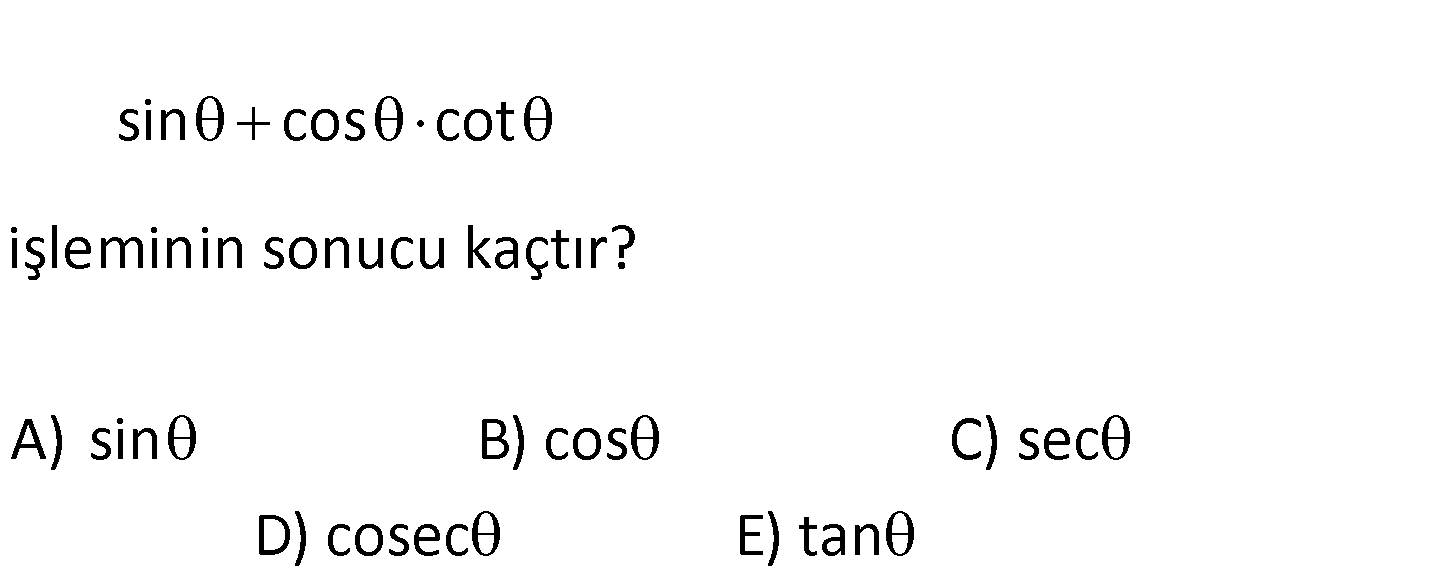
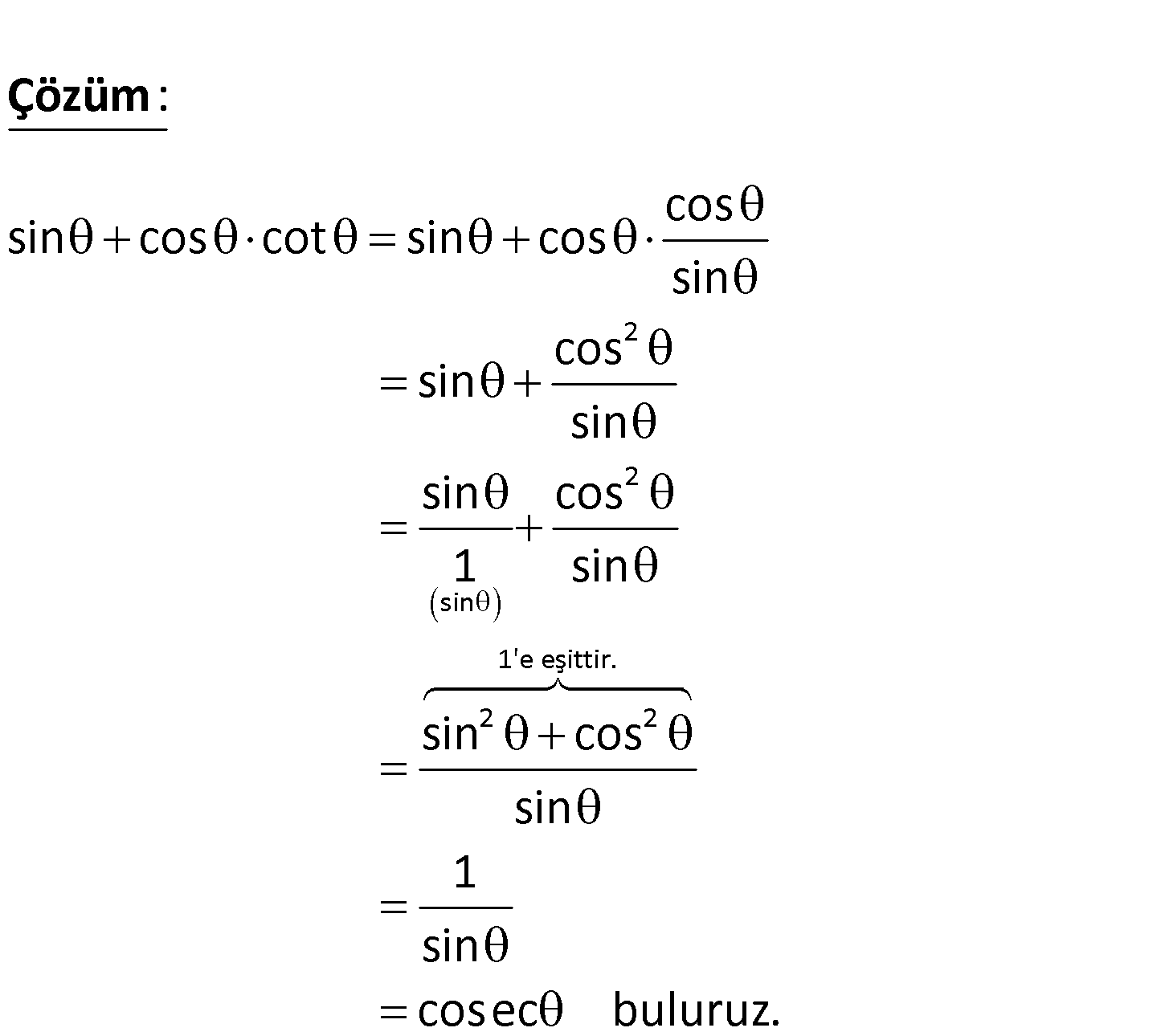
3.SORU
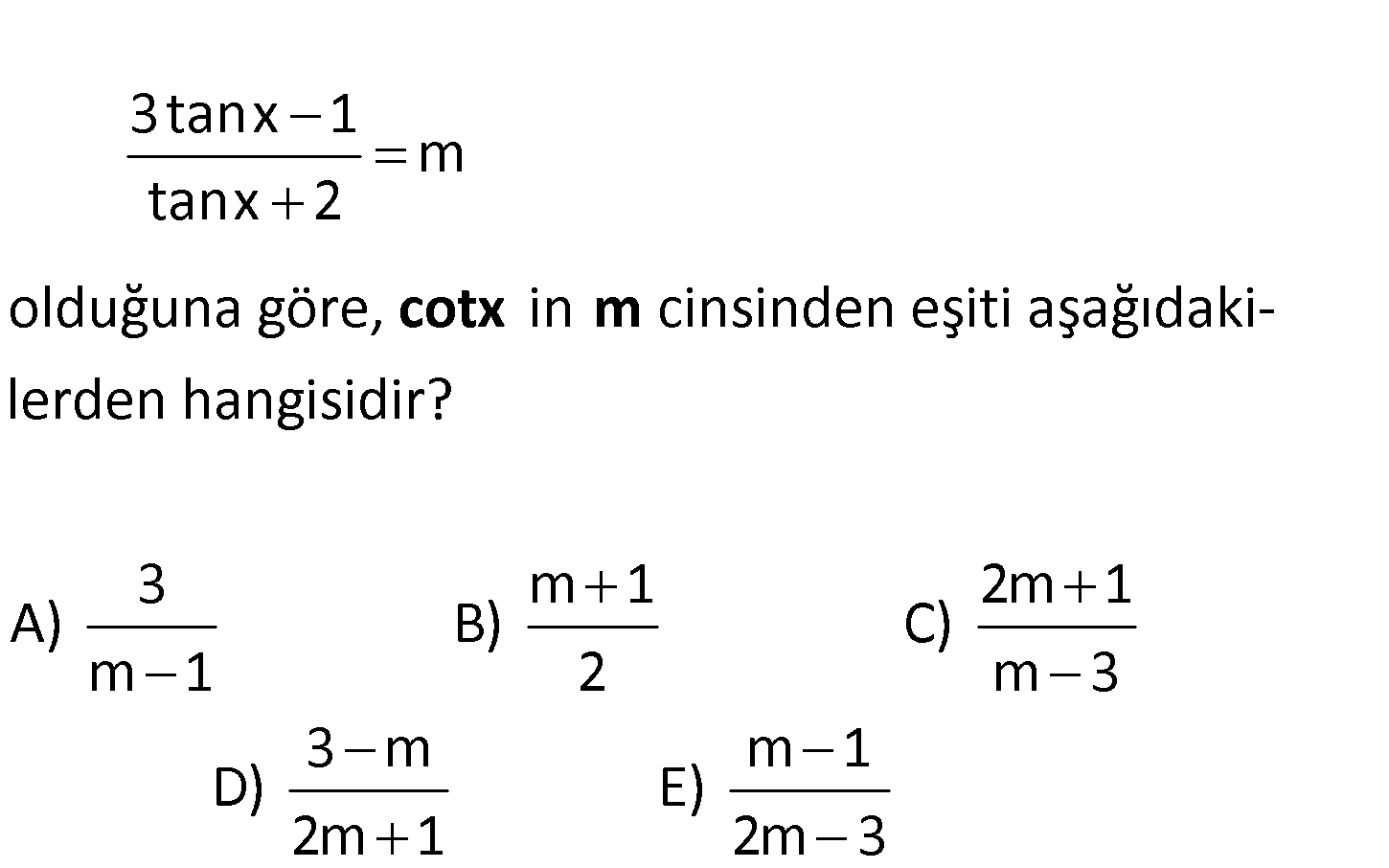
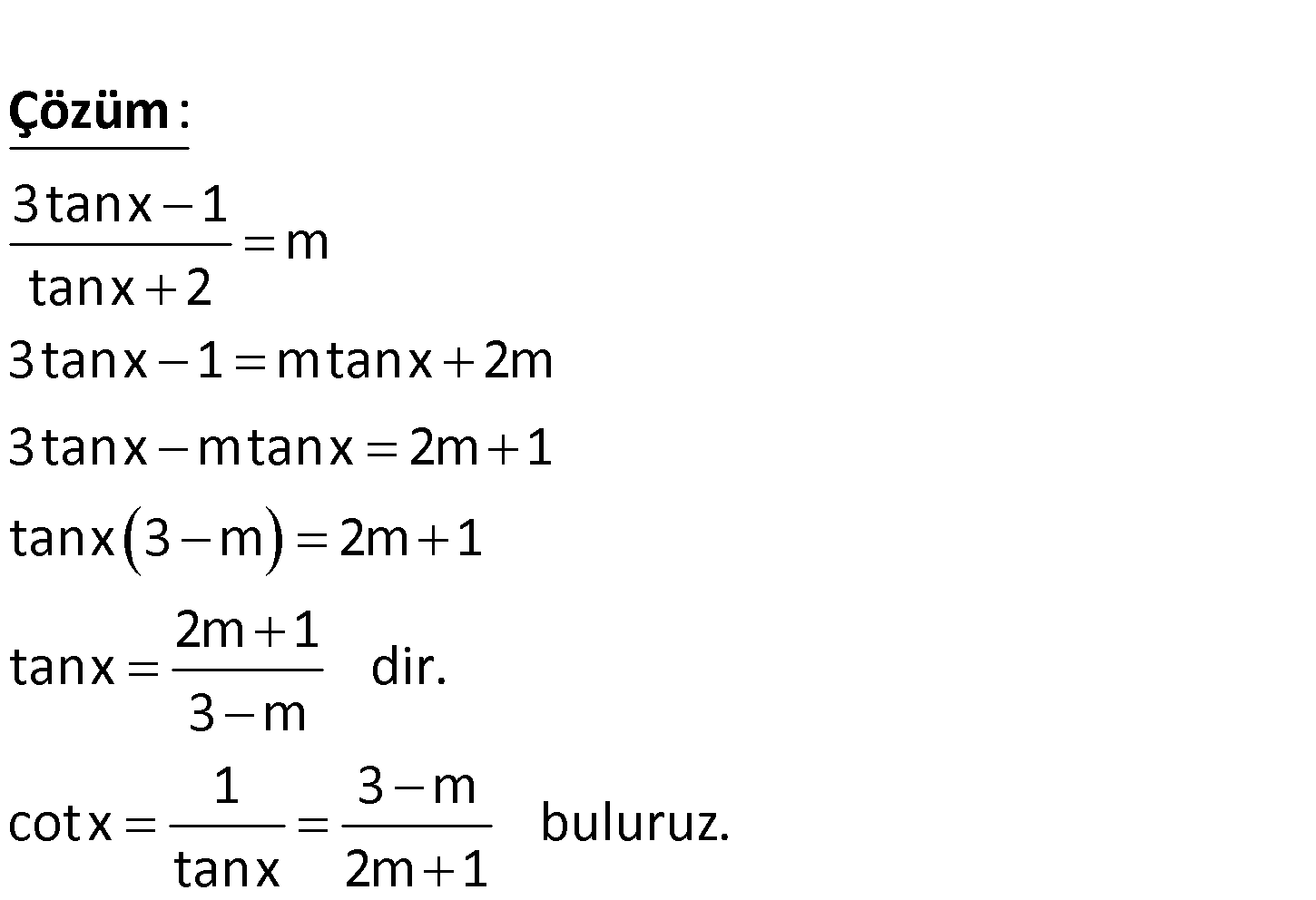
4.SORU
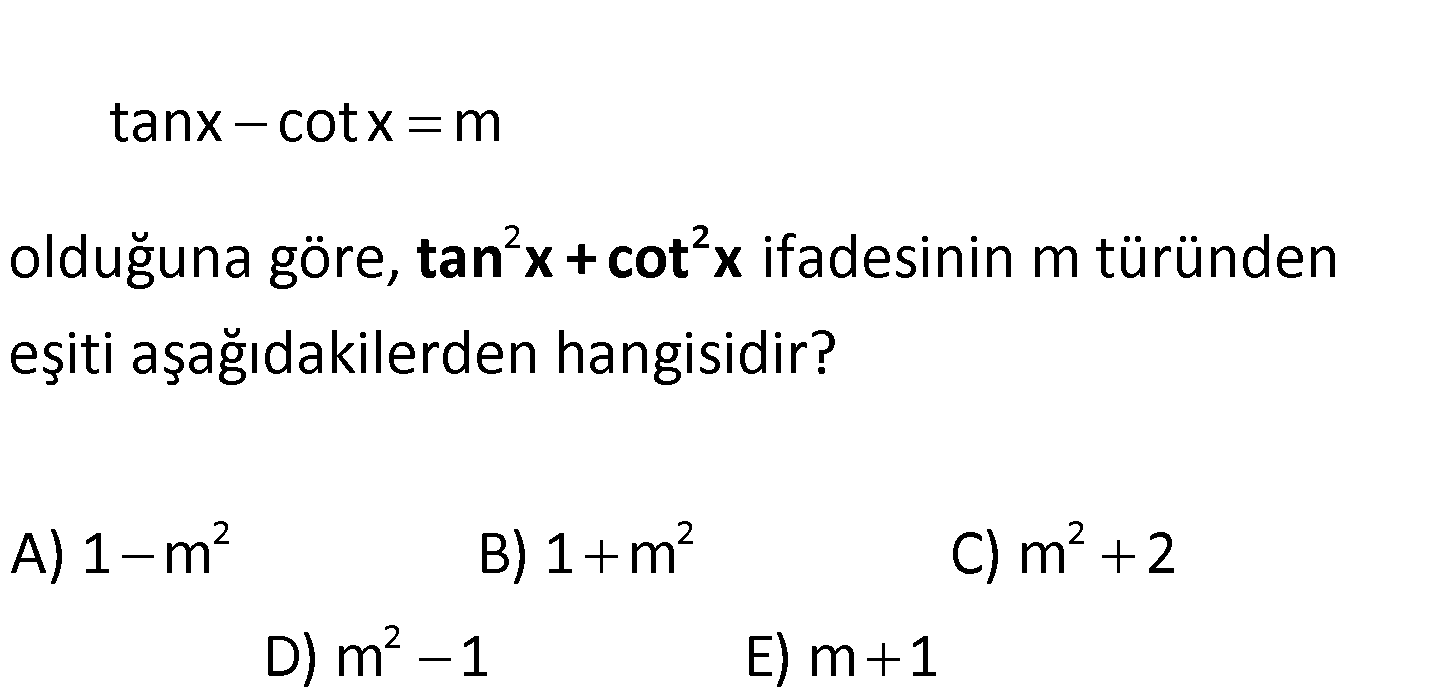

5.SORU
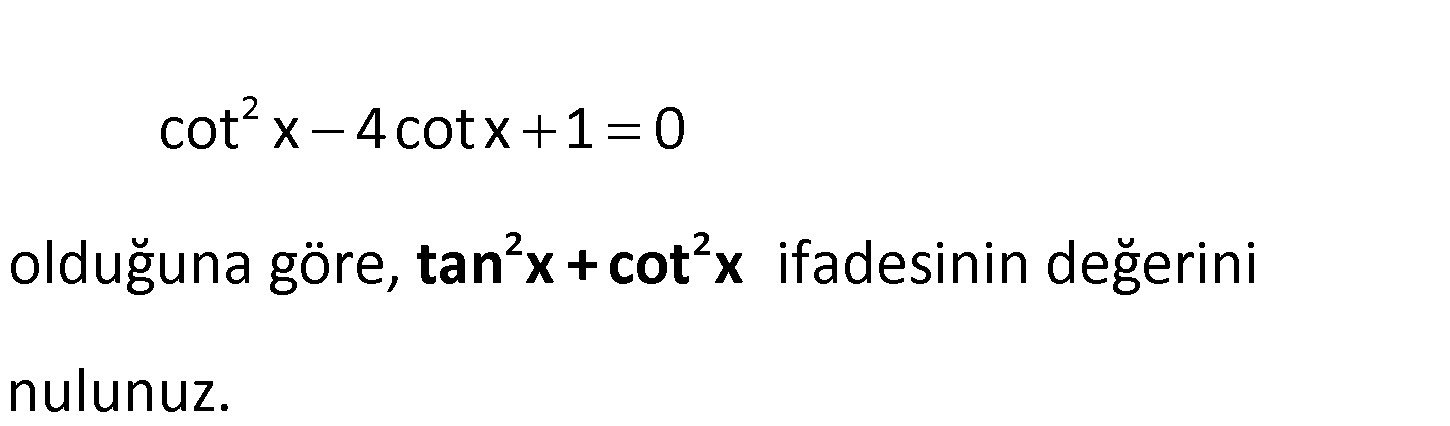

6.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
tanx cotx 3 ise kaçtır? 2 2 tan x + cot x Eşitliğin iki tarafının karesini tanx cotx 3 : ala Çözüm 2 2 1 2 2 lım. tan x 2. tanx.cotx cot x 9 tan x cot x 9 2 7 bulunur. 44
sin cos cot işleminin sonucu kaçtır? A) sin B) cos C) sec D) cosec E) tan www.matematikkolay.net 2 cos sin cos cot sin cos sin cos sin : sin Çözüm 2 sin 1’e eşittir. 2 2 sin cos 1 sin sin cos sin 1 sin cosec buluruz. 48
3tanx 1 m tanx 2 olduğuna göre, in cinsinden eşiti aşağıdakilerden hangisidir? 3 A) cotx m m 1 2m 1 B) C) m 1 2 m 3 3 m m 1 D) E) 2m 1 2m 3 3tanx 1 m tanx 2 3tanx 1 mtanx 2m 3tanx mtanx 2m 1 tanx 3 m 2m 1 2m 1 tanx dir. 3 m 1 3 m cotx ta x : n Çözüm buluruz. 2m1 71
2 tanx cotx m olduğuna göre, ifadesinin m türünden eşiti aşağıdakilerden hangisidir 2 tan x + cot x 2 2 2 2 ? A) 1 m B) 1 m C) m 2 D) m 1 E) m 1 2 2 2 1 tanx cotx m her iki tarafın karesini alalım. (tanx cotx) m tan x 2tanx.cotx t : co Çözüm 2 2 2 2 2 2 2 2 x m (Not: tanx ile cotx’in çarpımı 1 dir.) tan x 2 cot x m tan x cot x m 2 buluruz. Doğru Cevap: E şıkkı www.matematikkolay.net 97
2 cot x 4cotx 1 0 olduğuna göre, ifadesinin değerini nulunuz. 2 2 tan x + cot x 2 2 tanx cot x 4cotx 1 0 (her tarafı cot x ‘e bölelim.) cot x 4cotx 1 0 cotx cotx cotx 1 cotx 4 cotx t : co Çözüm 2 2 2 2 1 2 2 x tanx 4 (her tarafın karesini alalım) (cotx tanx) 4 cot x 2.cotx. tanx tan x 16 cot x tan x 16 2 14 buluruz. 123
4 4 tanx cotx 3 olduğuna göre, tan x cot x ifadesinin değeri kaçtır? A) 3 B) 23 C) 35 D) 47 E) 81 2 2 1 2 2 tanx cotx 3 iki tarafın karesini alalım. tan x 2. tanx.cotx cot x 9 tan x cot x 9 2 7 k : İ i Çözüm 4 2 2 4 1 4 4 4 4 tarafın karesini alalım. tan x 2. tan x.cot x cot x 49 tan x cot x 49 2 tan x cot x 47 bulunur. 137

