Her (![]() ) ve Bazı (
) ve Bazı (![]() ) Niceleyicileri
) Niceleyicileri
Açık Önerme
İçinde en az bir değişken bulunan ve bu değişkenlere verilen değerlerle doğru ya da yanlış olduğu belirlenen önermelere açık önerme denir.
Bir açık önermeyi doğrulayan elemanların kümesine o açık önermenin doğruluk kümesi denir.
Bir a sayısı p(x) açık önermesinin doğruluk kümesinin elemanı ise p(a)![]() 1 dir.
1 dir.
Bir b sayısı p(x) açık önermesinin doğruluk kümesinin elemanı değil ise
p(b) ![]() 0 dır.
0 dır.
Örnek 28
p(x) : “x bir tam sayı, x²=9” açık önermesi için
Doğruluk kümesini bulunuz.
Çözüm
x² =9 denklemini sağlayan 3 ve -3 tam sayıları bu açık önermenin doğruluk kümesini oluşturur. Doğruluk kümesi D olmak üzere D={-3 , 3} ile gösterilir.
p(3) , p(-2) , p(0) ifadelerinin doğruluk değerlerini bulunuz.
Çözüm
x =3 için 3² =9 ve 9=9 olduğundan p(3) ![]() 1 olur.
1 olur.
x =-2 için (-2)² =4 ve 4 ≠ 9 olduğundan p(-2) ![]() 0 olur.
0 olur.
x =0 için 0² =0 ve 0 ≠ 9 olduğundan p(0) ![]() 0 olur.
0 olur.
Not:
Her denklem ve her eşitsizlik aynı zamanda bir açık önerme belirtir.
Denklemler ve eşitsizliklerin çözüm kümeleri ise bu açık önermelerin doğruluk kümesidir.
Örnek 29
Aşağıda verilen açık önermelerin doğruluk kümelerini bulunuz.
p(x) : “x bir tam sayı, 5 ≤ x < 12”
Çözüm
p önermesinin doğruluk kümesi, D={5, 6, 7, 8, 9, 10, 11} olur.
q(x) : “x bir doğal sayı, 2 < x² < 20”
Çözüm
q önermesinin doğruluk kümesi, D={2, 3, 4} olur.
r(x) : “x bir pozitif tam sayı, 3x – 2 ≤ 7”
Çözüm
![]()
![]()
![]()
olup r önermesinin doğruluk kümesi, D={1, 2, 3} olur.
s(x) : “x bir gerçek sayı, 2x + 3 . (x – 1) =7”
Çözüm
2x + 3x – 3 =7
5x – 3 + 3 =7 + 3
5x =10
x =2
olup s önermesinin doğruluk kümesi, D ={2} olur.
Niceleyiciler
“Her” sözcüğü, bütün ve tamamı sözcükleri ile aynı anlamdadır.
“Her” niceleyicisi, önüne geldiği elemanların tamamını anlattığı için bu niceleyiciye evrensel niceleyici denir ve “![]() ” sembolü ile gösterilir.
” sembolü ile gösterilir.
“Bazı” sözcüğü, en az bir ifadesi ile aynı anlamdadır.
“Bazı” niceleyicisi, en az bir tane anlamında kullanıldığı için bu niceleyiciye varlıksal niceleyici denir ve “ ![]() ” sembolü ile gösterilir.
” sembolü ile gösterilir.
Not:
Doğal sayılar kümesi ![]() ,
,
tam sayılar kümesi ![]() ,
,
rasyonel sayılar kümesi ![]() ,
,
gerçek sayılar kümesi ![]() sembolleri ile gösterilir.
sembolleri ile gösterilir.
Örnek 30
“![]() ” sözel olarak ifade edelim.
” sözel olarak ifade edelim.
Çözüm
“Her pozitif tam sayının karesi sıfırdan büyüktür.” şeklinde ifade edilir.
Örnek 31
![]() ” sözel olarak ifade edelim.
” sözel olarak ifade edelim.
Çözüm
‘‘Bazı tam sayıların 2 eksiği 8 e eşit veya 8 den küçüktür.” veya ‘‘ En az bir tam sayının 2 eksiği 8 e eşit veya 8 den küçüktür.” şeklinde ifade edilir.
Örnek 32
Aşağıda verilen önermeleri sembolik mantık kullanarak yazıp önermelerin doğruluk değerlerini bulunuz.
p : ‘‘Her tam sayı kendisinin karesinden küçüktür.’’
Çözüm
![]() şeklinde ifade edilir. Bu kurala uymayan herhangi bir tam sayının bulunması bu önermenin doğruluk değerini 0 yapar. 0 ve 1 tam sayıları için bu açık önerme yanlıştır ve p
şeklinde ifade edilir. Bu kurala uymayan herhangi bir tam sayının bulunması bu önermenin doğruluk değerini 0 yapar. 0 ve 1 tam sayıları için bu açık önerme yanlıştır ve p ![]() 0 olur.
0 olur.
q : ‘‘Bazı gerçek sayıların 3 fazlası 7 den büyüktür.’’
Çözüm
![]() şeklinde ifade edilir. Bu kurala uyan herhangi bir gerçek sayının bulunması bu önermenin doğruluk değerini 1 yapar. Örneğin 5 sayısı için bu açık önerme doğrudur ve q
şeklinde ifade edilir. Bu kurala uyan herhangi bir gerçek sayının bulunması bu önermenin doğruluk değerini 1 yapar. Örneğin 5 sayısı için bu açık önerme doğrudur ve q ![]() 1 olur.
1 olur.
Açık Önermenin Değili (Olumsuzu)
![]() x, p(x) açık önermesinin değili
x, p(x) açık önermesinin değili ![]() x,p'(x) tir. Bu özellik sembol ile
x,p'(x) tir. Bu özellik sembol ile
![]() şeklinde ifade edilir.
şeklinde ifade edilir.
![]() x,p(x) açık önermesinin değili
x,p(x) açık önermesinin değili ![]() x, p'(x) tir. Bu özellik sembol ile
x, p'(x) tir. Bu özellik sembol ile
![]() şeklinde ifade edilir.
şeklinde ifade edilir.

Örnek 33
p : ‘‘Her asal sayı bir doğal sayıdır.’’ önermesinin değilini bulunuz.
Çözüm
p’ : ‘‘Bazı asal sayılar bir doğal sayı değildir.’’
Örnek 34
Aşağıda verilen önermelerin değilini bulunuz.
![]()
Çözüm
![]()
![]()
Çözüm
![]()
![]()
Çözüm
![]()
![]()
Çözüm
![]()
Örnek 35
Aşağıda verilen önermelerin değilini bulunuz.
![]()
Çözüm
![]()
![]()
Çözüm
![]()
Alıştırma-1
Aşağıda verilen açık önermelerin doğruluk kümelerini bulunuz.
![]()
Çözüm
Bir tam sayının karesi negatif olamaz. Bu sebeple ![]() her zaman sağlanır. Burayı incelemeye gerek yok.
her zaman sağlanır. Burayı incelemeye gerek yok. ![]() eşitsizliğini inceleyelim.
eşitsizliğini inceleyelim.
Burayı ise sadece -2, -1, 0, 1, 2 tam sayıları sağlar. Bu sebeple doğruluk kümesi D={-2, -1, 0, 1, 2} dir.
![]()
Çözüm
Sırayla en küçük pozitif tam sayıdan başlayalım.
![]() dir, sağlar.
dir, sağlar.
![]() dir, sağlar.
dir, sağlar.
![]() dir, sağlar.
dir, sağlar.
![]() dir, sağlamaz. Buna göre,
dir, sağlamaz. Buna göre,
D={1, 2, 3} tür.
![]()
Çözüm
![]()
![]()
![]()
![]() tir. Buna göre,
tir. Buna göre,
D={-3} tür.
Alıştırma-2
Aşağıda önermelerin değilini bulunuz.
![]()
Çözüm
![]()
![]()
Çözüm
![]()
Alıştırma-3
Aşağıda önermenin karşıt tersini bulunuz.
![]()
Çözüm
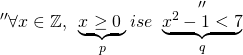
![]() karşıt tersi
karşıt tersi ![]() dür. Buna göre,
dür. Buna göre,
![]()
Alıştırma-4
Aşağıda önermenin değilini bulunuz.
![]()
Çözüm
![]()
![]()
![]()
![]()


çoq iyi
eyw abi çok iyi anladım sağol çok iyi anlatmışsın hocadan daha iyisin yeminle 😀 kolay gelsin 10. sınıftada böle bekliyom
Özge bu notları çok beğendi. Ellerinize sağlık.
Hocam merhabalar yeni başlamış bir öğretmen olarak bilgilerinizden faydalanırken her seferinde Allah razı olsun diyorum işimi çok kolaylaştırıyor Teşekkür ederim böyle net anlatım ve bilgiler için .