Üslü Denklem ve Eşitsizlikler Soru ve Çözümleri (Latex Formatı)

Bu bölümde Üslü Denklem ve Eşitsizlikler konusu ile ilgili 18 adet soru ve çözümleri bulunmaktadır. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…

Konu Anlatımı için Tıkla
Üslü Denklem ve Eşitsizlikler Çözümlü Soruları pdf indir
Kitap Formatında Görmek için Tıkla

ÜSLÜ DENKLEM VE EŞİTSİZLİKLER SORU VE ÇÖZÜMLERİ

SORU: 1)

$\displaystyle \begin{array}{l}\text{ }{{2}^{{a+3}}}=128\\\text{ }{{5}^{{2b-5}}}=125\end{array}$

olduğuna göre a+b kaçtır?

A) 4 B) 5 C) 6 D) 7 E) 8

ÇÖZÜM:

128 ve 125 sayılarını üslü sayı olarak ifade edelim;

$\displaystyle \begin{array}{l}128=\underbrace{{2.2.....2}}_{{7\text{ }\tan e}}={{2}^{7}}\\125=5.5.5={{5}^{3}}\text{ }t\ddot{u}r.\\{{2}^{{a+3}}}={{2}^{7}}\text{ }\Rightarrow tabanlar\text{ }ayn\imath \text{ }oldu\breve{g}undan\text{ }\ddot{u}sler\text{ }de\text{ }ayn\imath \\olmal\imath .\\a+3=7\text{ }\Rightarrow \text{ }a=4\text{ }bulunur.\\\\{{5}^{{2b-5}}}={{5}^{3}}\text{ }\Rightarrow \text{ }2b-5=3\text{ }\Rightarrow \text{ }2b=8\text{ }\Rightarrow \text{ }b=4\text{ }t\ddot{u}r.\\O\text{ }halde;\\a+b=4+4=8\text{ }buluruz.\\\end{array}$

Doğru Cevap : E şıkkı

SORU:2)

$\displaystyle {{\text{(}0,2)}^{{x+8}}}={{(0,04)}^{{x+3}}}$

olduğuna göre, x kaçtır?

A) 2 B) 3 C) 4 D) 5 E) 6

ÇÖZÜM:

Ondalık kesirleri rasyonel sayıya çevirerek çözüme başlayalım.

$\displaystyle \begin{array}{l}{{(0,2)}^{{x+8}}}={{(0,04)}^{{x+3}}}\\{{\left( {\frac{2}{{10}}} \right)}^{{x+8}}}={{\left( {\frac{4}{{100}}} \right)}^{{x+3}}}\text{ }sadelestire\lim ,\text{ }\\\,\ {{\left( {\frac{1}{5}} \right)}^{{x+8}}}={{\left( {\frac{1}{{25}}} \right)}^{{x+3}}}\text{ }\left( {\text{ }\frac{1}{{25}}={{{\left( {\frac{1}{5}} \right)}}^{2}}} \right)\\\ \ {{\left( {\frac{1}{5}} \right)}^{{x+8}}}={{\left( {{{{\left( {\frac{1}{5}} \right)}}^{2}}} \right)}^{{x+3}}}\text{ }\\\ \ {{\left( {\frac{1}{5}} \right)}^{{x+8}}}={{\left( {\frac{1}{5}} \right)}^{{2.(x+3)}}}\text{ }Tabanlar\text{ }ayn\imath ,\text{ }\ddot{u}sler\text{ }esit\text{ }olmal\imath \\\ \ \ \ \ x+8=2.(x+3)\\\ \ \ \ \ x+8=2x+6\\\ \ \ \ \ 8-6=2x-x\\\ \ \ \ \ \ \ \ \ \ 2=x\text{ }\Rightarrow \text{ }x=2\text{ }bulunur.\end{array}$

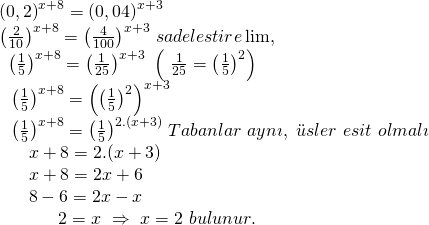
Doğru Cevap : A şıkkı

SORU:3)

$\displaystyle \text{ }{{3.2}^{{x+1}}}+{{6.2}^{{x-1}}}+{{2}^{x}}=160$

eşitliğini sağlayan x değeri aşağıdakilerden

hangisidir?

A) 1 B) 2 C) 3 D) 4 E) 5

ÇÖZÜM:

Üssü en küçük olan terimin ortak parantezine alarak soruyu çözelim. Bunun için diğer terimleri

$\displaystyle {{2}^{{x-1}}}$ terimine kadar açmak gerekir,

$\displaystyle \begin{array}{l}{{3.2}^{{x+1}}}+{{6.2}^{{x-1}}}+{{2}^{x}}=160\\{{3.2}^{2}}{{.2}^{{x-1}}}+{{6.2}^{{x-1}}}+{{2}^{1}}{{.2}^{{x-1}}}=160\\\text{ }{{12.2}^{{x-1}}}+{{6.2}^{{x-1}}}+{{2.2}^{{x-1}}}=160\\\text{ }{{2}^{{x-1}}}.(12+6+2)=160\\\text{ }{{2}^{{x-1}}}.20=160\\\text{ }{{2}^{{x-1}}}=8\\\text{ }{{2}^{{x-1}}}={{2}^{3}}\\\text{ }x-1=3\\\text{ }x=4\text{ }buluruz.\end{array}$

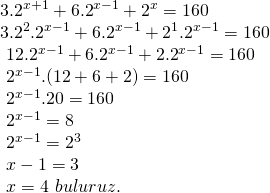
Doğru Cevap : D şıkkı

SORU:4)

$\displaystyle {{\text{3}}^{{2a-3}}}+\frac{2}{{{{3}^{{3-2a}}}}}=81$

eşitliğini sağlayan a değeri aşağıdakilerden

hangisidir?

A) 1 B) 2 C) 3 D) 4 E) 5

ÇÖZÜM:

Payda eşitleyerek soruyu çözmeye çalışalım,

$\displaystyle \begin{array}{*{20}{r}} {{{\text{3}}^{{2a-3}}}+\frac{2}{{{{3}^{{3-2a}}}}}} & = & {81} \\ {\underset{{({{3}^{{3-2a}}})}}{\mathop{{\frac{{{{\text{3}}^{{2a-3}}}}}{1}}}}\,+\underset{{(1)}}{\mathop{{\frac{2}{{{{3}^{{3-2a}}}}}}}}\,} & = & {81} \\ {\frac{{{{3}^{{2a-3}}}{{{.3}}^{{3-2a}}}+2}}{{{{3}^{{3-2a}}}}}} & = & {81} \\ {\frac{{{{3}^{{2a-3}}}^{{+3-2a}}+2}}{{{{3}^{{3-2a}}}}}} & = & {81} \\ {\frac{{{{3}^{0}}+2}}{{{{3}^{{3-2a}}}}}} & = & {81} \\ {\frac{{1+2}}{{{{3}^{{3-2a}}}}}} & = & {81} \\ {\frac{{{{3}^{1}}}}{{{{3}^{{3-2a}}}}}} & = & {81} \\ {{{3}^{{1-(3-2a)}}}} & = & {81} \\ {{{3}^{{1-3+2a}}}} & = & {{{3}^{4}}} \\ {-2+2a} & = & 4 \\ {2a} & = & 6 \\ a & = & 3 \end{array}$

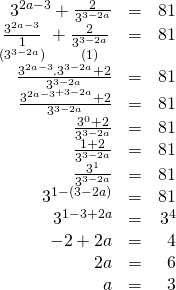
a yı 3 olarak buluruz.

Doğru Cevap : C şıkkı

SORU:5)

$\displaystyle {{(2x+3)}^{4}}={{5}^{4}}$

eşitliğini sağlayan x değerlerinin toplamı aşağıdakilerden hangisidir?

$\displaystyle \begin{array}{*{20}{l}} {A)\text{ }-1\text{ }} & {B)\text{ }-2} & {C)\text{ }-3} & {D)\text{ }-4} & {E)\text{ }-5} \end{array}$

ÇÖZÜM:

İki denklemde de üsler çiftse tabandaki ifadeler hem pozitif hem de negatif işaretli olarak birbirlerine eşittir. Yani;

$\displaystyle {{x}^{{2n}}}={{y}^{{2n}}}\text{ }ise\text{ }x=y\text{ }veya\text{ }x=-y\text{ }dir.\text{ }O\text{ }halde;$

$\displaystyle \begin{array}{*{20}{c}} {2x+3=5} & {ve} & {2x+3=-5} \\ {2x=2} & {} & {2x=-8} \\ {x=1} & {} & {x=-4} \end{array}$

$\displaystyle De\breve{g}erlerin\text{ }toplam\imath =1+(-4)=-3\text{ }olarak\text{ }bulunur$

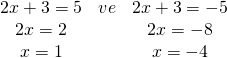
Doğru Cevap : C şıkkı

SORU:6)

$\displaystyle {{(x+2)}^{{16}}}={{(4x+8)}^{8}}$

eşitliğini sağlayan farklı x değerlerinin çarpımı kaçtır?

$\displaystyle \begin{array}{*{20}{l}} {A)\text{ }-12} & {B)\text{ }-2} & {C)\text{ }12} & {D)\text{ }24} & {E)\text{ }48} \end{array}$

ÇÖZÜM:6)

$\displaystyle {{(x+2)}^{{16}}}={{(4x+8)}^{8}}$ ifadesindeki üslerin çift olduğuna

dikkat edelim.Üsleri aynı olacak şekilde eşitliğin sol tarafında bir düzenleme yapalım;

$\displaystyle \begin{array}{l}{{(x+2)}^{{16}}}={{(4x+8)}^{8}}\text{ }\Rightarrow \text{ }{{\left[ {{{{(x+2)}}^{2}}} \right]}^{8}}={{(4x+8)}^{8}}\\\underline{{1.durum}}:{{(x+2)}^{2}}=4x+8\\{{x}^{2}}+4x+4=4x+8\\{{x}^{2}}-4=0\text{ }(iki\text{ }kare\text{ }fark\imath )\\(x-2).(x+2)=0\text{ }\Rightarrow \text{ }Buna\text{ }g\ddot{o}re\text{ }x=2\text{ }veya\text{ }-2\text{ }dir.\\\\\underline{{2.durum}}:\text{ }{{(x+2)}^{2}}=-(4x+8)\\{{x}^{2}}+4x+4=-4x-8\\{{x}^{2}}+8x+12=0\\x\text{ }6\\x\text{ }2\\(x+2).(x+6)=0\text{ }\Rightarrow \text{ }Buna\text{ }g\ddot{o}re\text{ }x=-2\text{ }veya\text{ }-6\text{ }d\imath r.\\\\x'in\text{ }alabilece\breve{g}i\text{ }farkl\imath \text{ }de\breve{g}erler\text{ }2,-2\text{ }ve\text{ }-6\text{ }d\imath r.\\Carp\imath mlar\imath =2.(-2).(-6)=24\text{ }bulunur.\end{array}$

Doğru Cevap : D şıkkı

SORU:7)

$\displaystyle {{(2x-4)}^{{15}}}={{(x+2)}^{{15}}}$

eşitliğini sağlayan x değeri kaçtır?

A) 2 B) 3 C) 4 D) 5 E) 6

ÇÖZÜM:

Üsler aynı ve tek olunca tabandaki terimlerin eşit olması gerekir.

$\displaystyle \begin{array}{l}{{(2x-4)}^{{15}}}={{(x+2)}^{{15}}}\text{ ise }\\\text{ 2x}-4=x+2\\\text{ }2x-x=2+4\\\text{ }x=6\text{ buluruz}\text{.}\end{array}$

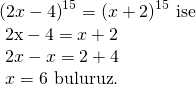
Doğru Cevap : E şıkkı

SORU:8)

$\displaystyle \begin{array}{l}x,y\in Z\text{ }olmak\text{ }\ddot{u}zere\\{{7}^{{3x+y-14}}}={{8}^{{x+2y-8}}}\text{ }ise,\text{ }x.y\text{ c}arp\imath m\imath \text{ }kact\imath r?\end{array}$

A) 6 B) 8 C) 14 D) 16 E) 24

ÇÖZÜM:

8) $\displaystyle {{7}^{{3x+y-14}}}={{8}^{{x+2y-8}}}$ eşitliği sadece üslerin 0 olduğu durumda birbirine eşittir. O halde;

$\displaystyle \begin{array}{l}3x+y-14=0\\x+2y-8=0\text{ }d\imath r.\text{ }Bu\text{ }denklemleri\text{ c}\ddot{o}ze\lim .\\\\\text{ }1\text{ }/\text{ }3x+y-14=0\\\text{ }\underline{{\text{ }+\text{ }-3/\text{ }x+2y-8=0\text{ }}}\\\text{ }3x+y-14=0\\\text{ }\underline{{\text{ }+\text{ }-3x-6y+24=0\text{ }}}\\\text{ }\ \ \ \ \ \ \ \ \ \ \ \text{ }-5y+10=0\\\text{ }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ }-5y=-10\\y=2\text{ }bulunur.\text{ }x+2y-8=0\text{ }ise\text{ }x+4-8=0\text{ }\\x-4=0\text{ }\Rightarrow \text{ }x=4\text{ }bulunur.\text{ }Buna\text{ }g\ddot{o}re;\\x.y=4.2=8\text{ }buluruz.\end{array}$

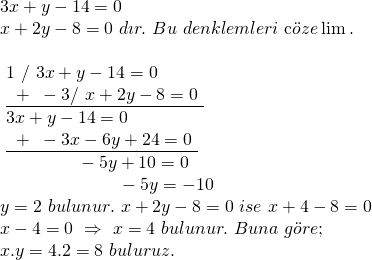
Doğru Cevap : B şıkkı

SORU: 9)

$\displaystyle {{(a-5)}^{{{{a}^{2}}-5a}}}=1$

denkleminin çözüm kümesi aşağıdakilerden hangisidir?

$\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }\{-4,\text{ }0\}\text{ }} & {B)\text{ }\{0,\text{ }5,\text{ }6\}} & {C)\text{ }\{0,\text{ }6\}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }\{-4,\text{ }0,\text{ 5}\text{, }6\}} & {E)\text{ }\{0,\text{ }4,\text{ }6\}} \end{array}\end{array}$

ÇÖZÜM:

$\displaystyle {{x}^{n}}=1$ eşitliklerinde 3 farklı durum söz konusudur.

$\displaystyle \begin{array}{l}1.durum:\text{ }x\ne 0\text{ }ise\text{ }n=0\text{ }d\imath r.\\2.durum:\text{ }x=1\text{ }ise,\text{ }n\in R\text{ }dir.\\3.durum:\text{ }x=-1\text{ }ise,\text{ }n\text{ c}ift\text{ }say\imath d\imath r.\end{array}$

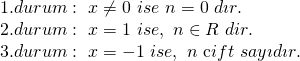
Buna göre;

$\displaystyle {{(a-5)}^{{{{a}^{2}}-5a}}}=1$

eşitliğindeki üç durumu inceleyelim;

$\displaystyle \underline{{1.durum:}}\text{ }{{a}^{2}}-5a=0\text{ }\Rightarrow \text{ }a.(a-5)=0$

buradan a= 0 ve a= 5 kökleri bulunur. Ancak a 5 olduğunda üslü sayının tabanı 0 olacağından 5’i kullanamayız.

$\displaystyle \underline{{2.durum:}}\text{ }a-5=1\text{ }\Rightarrow \text{ }a=6\text{ }buluruz.\text{ }a=6\text{ }durumu$

üssün reel sayı olmasını engellemediği için 6’yı kök olarak alabiliriz.

$\displaystyle \underline{{3.durum:}}\text{ }a-5=-1\text{ }\Rightarrow \text{ }a=4\text{ }buluruz.\text{ }a=4\text{ }oldu\breve{g}un$

da üs : $\displaystyle {{a}^{2}}-5a={{4}^{2}}-5.4=16-20=-4$ olur. Çift sayı olduğundan a 4 kökünü alabiliriz.

O halde çözüm kümesi $\displaystyle =\{0,\text{ }4,\text{ }6\}$ dır

Doğru Cevap : E şıkkı

SORU:10)

$\displaystyle \left. \begin{array}{l}{{3}^{x}}=125\\{{5}^{y}}=81\end{array} \right\}\text{ }$

olduğuna göre x.y çarpımı kaçtır?

A) 10 B) 12 C) 15 D) 18 E) 27

ÇÖZÜM:

Bu soruda 1.denklemde 5 sayısının x cinsinden ifadesini bulup, 2.denklemde yerine yazalım.

$\displaystyle \begin{array}{l}{{3}^{x}}=125\text{ }\Rightarrow \text{ }{{3}^{x}}={{5}^{3}}\text{ }\Rightarrow \text{ }{{3}^{{\frac{x}{3}}}}=5\text{ }bunu\text{ }2.denk-\\lemde\text{ }5'in\text{ }yerine\text{ }yazal\imath m.\\{{5}^{y}}=81\text{ }idi,\\{{\left( {{{3}^{{\frac{x}{3}}}}} \right)}^{y}}=81\text{ }\Rightarrow {{3}^{{\frac{{x.y}}{3}}}}={{3}^{4}}\Rightarrow \frac{{x.y}}{3}=4\Rightarrow x.y=12\text{ }dir.\end{array}$

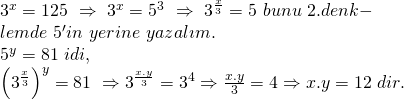
Doğru Cevap : B şıkkı

SORU:11)

$\displaystyle \left. \begin{array}{l}{{7}^{{x-y}}}=4\\{{7}^{{x+1}}}=56\end{array} \right\}$

olduğuna göre $\displaystyle {{\text{7}}^{y}}$ kaçtır?

A) 2 B) 4 C) 6 D) 7 E) 16

ÇÖZÜM:

$\displaystyle \begin{array}{l}{{7}^{{x-y}}}=4\\{{7}^{{x+1}}}=56\end{array}$

İkinci denklemden $\displaystyle {{7}^{x}}$ in neye eşit olduğunu bulursak, 1.denklemden $\displaystyle {{7}^{y}}$ yi bulabiliriz. Buna göre;

$\displaystyle \begin{array}{l}{{7}^{{x+1}}}=56\ \ \ \ \Rightarrow \ \ \ \ {{7}^{x}}.7=56\ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ {{7}^{x}}=8\text{ }buluruz.\\{{7}^{{x-y}}}=4\ \ \ \ \ \ \Rightarrow {{7}^{x}}{{.7}^{{-y}}}=4\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow \frac{{{{7}^{x}}}}{{{{7}^{y}}}}=4\text{ }\Rightarrow \frac{8}{{{{7}^{y}}}}=4\Rightarrow {{7}^{y}}=2\text{ }bulunur.\end{array}$

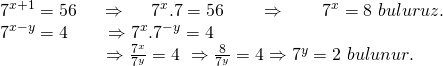
Doğru Cevap :A şıkkı

SORU:12)

$\displaystyle \left. \begin{array}{l}{{2}^{a}}{{.3}^{b}}=72\\{{3}^{a}}{{.2}^{b}}=108\end{array} \right\}$

olduğuna göre, a+b toplamının sonucu kaçtır?

A) 3 B) 4 C) 5 D) 6 E) 7

ÇÖZÜM:

$\displaystyle \begin{array}{l}{{2}^{a}}{{.3}^{b}}=72\\{{3}^{a}}{{.2}^{b}}=108\end{array}$

iki denklemi taraf tarafa çarparsak buradan üsler toplamını elde edebiliriz.

$\displaystyle \begin{array}{l}\ \ \ \ \ \ {{2}^{a}}{{.3}^{b}}=72\\\underline{{\ x\ \ \ {{3}^{a}}{{{.2}}^{b}}=108\ \ \ }}\\{{2}^{a}}{{.3}^{b}}{{.3}^{a}}{{.2}^{b}}=72.108\\{{2}^{a}}{{.2}^{b}}{{.3}^{a}}{{.3}^{b}}=72.108\\\ \ \ {{2}^{{a+b}}}{{.3}^{{a+b}}}=72.108\\\ \ \ \ \ \ \ \ \ {{6}^{{a+b}}}=\underbrace{{72}}_{{36.2}}.\underbrace{{108}}_{{36.3}}\\\ \ \ \ \ \ \ \ {{6}^{{a+b}}}=36.2.36.3\\\ \ \ \ \ \ \ \ {{6}^{{a+b}}}={{6}^{2}}{{.2.6}^{2}}.3\\\ \ \ \ \ \ \ \ {{6}^{{a+b}}}={{6}^{2}}{{.6}^{2}}.6\\\ \ \ \ \ \ \ \ {{6}^{{a+b}}}={{6}^{5}}\text{ }\Rightarrow \text{ }a+b=5\text{ }buluruz.\end{array}$

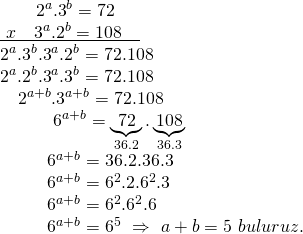
Doğru Cevap : C şıkkı

SORU:13)

$\displaystyle \left. \begin{array}{l}{{11}^{a}}+{{5}^{b}}=85\\{{2.11}^{a}}+{{5}^{b}}=45\end{array} \right\}$

olduğuna göre, b kaçtır?

A) 3 B) 4 C) 5 D) 6 E) 7

ÇÖZÜM:

$\displaystyle \begin{array}{l}{{11}^{a}}+{{5}^{b}}=85\\{{2.11}^{a}}+{{5}^{b}}=45\end{array}$

denklemlerinde 11 lı ifadeyi yok ederek çözmeye çalışalım.

$\displaystyle \begin{array}{l}-2\text{ }/{{11}^{a}}+{{5}^{b}}=85\\\underline{{\text{ }+\text{ }{{{2.11}}^{a}}+{{5}^{b}}=45\text{ }}}\\\ \ \ \ -{{2.11}^{a}}-{{2.5}^{b}}=-170\\\text{ }\underline{{+\text{ }{{{2.11}}^{a}}+{{5}^{b}}=45\ \ \ \ \ \ \ }}\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -{{5}^{b}}=-125\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{5}^{b}}={{5}^{3}}\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b=3\text{ }bulunur\end{array}$

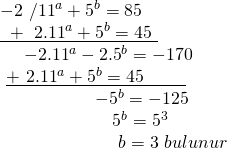
Doğru Cevap : A şıkkı

SORU:14)

$\displaystyle \text{ }{{2}^{{3x+5}}}>{{2}^{{x+15}}}$

eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?

$\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }(-5,\text{ }\infty )\text{ }} & {B)\text{ }(-5,\text{ 5})} & {C)\text{ }(-\infty ,\text{ 5})} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }(5,\text{ }\infty )} & {E)\text{ }\!\![\!\!\text{ }5,\text{ }\infty )} \end{array}\end{array}$

ÇÖZÜM:

Üslü sayılarda taban 1 den büyükse, büyük olan sayınının üssü de büyüktür. Buna göre;

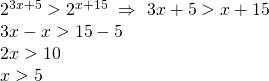$\displaystyle \begin{array}{l}{{2}^{{3x+5}}}>{{2}^{{x+15}}}\text{ }\Rightarrow \text{ }3x+5>x+15\\3x-x>15-5\\2x>10\\x>5\end{array}$ bulunur. O halde Ç.K. $\displaystyle =(5,\text{ }\infty )$ dur.

Doğru Cevap : D şıkkı

SORU:15)

$\displaystyle {{\left( {\frac{1}{3}} \right)}^{{a+2}}}<{{\left( {\frac{1}{3}} \right)}^{{2a-4}}}$

olduğuna göre, a’nın alabileceği en büyük tam sayı değeri kaçtır?

A) 1 B) 2 C) 3 D) 4 E) 5

ÇÖZÜM:

$\displaystyle {{\left( {\frac{1}{3}} \right)}^{{a+2}}}<{{\left( {\frac{1}{3}} \right)}^{{2a-4}}}$

Taban 0 ile 1 arasında bir değer ise büyük olan üslü sayının üssü küçük olmalıdır.Buna göre;

$\displaystyle \begin{array}{l}\ \ a+2>2a-4\\a-2a>-4-2\\\ \ \ \ -a>-6\\\ \ \ \ \ \ \ a<6\text{ }\end{array}$

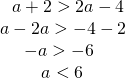
Buna göre; a’nın en büyük tam sayı değeri 5’tir.

Doğru Cevap: E şıkkı

SORU:16)

$\displaystyle \text{ }\begin{array}{*{20}{l}} {a={{8}^{7}}} \\ {b={{4}^{{13}}}} \\ {c={{{64}}^{2}}} \end{array}$

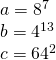
olduğuna göre, aşağıdaki sıralamalardan hangisi doğrudur?

$\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }a<b<c\text{ }} & {B)\text{ }a<c<b} & {C)\text{ }b<a<c} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }c<a<b} & {E)\text{ }c<b<a} \end{array}\end{array}$

ÇÖZÜM:

Sayıların tabanlarını aynı yapmaya çalışalım. Burdaki üslü sayıları 2 tabanında ifade edebiliriz.

$\displaystyle \begin{array}{*{20}{l}} {a={{8}^{7}}={{{({{2}^{3}})}}^{7}}={{2}^{{21}}}} \\ {b={{4}^{{13}}}={{{({{2}^{2}})}}^{{13}}}={{2}^{{26}}}} \\ {c={{{64}}^{2}}={{{({{2}^{6}})}}^{2}}={{2}^{{12}}}} \end{array}$

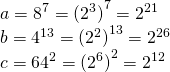
Taban 1’den büyük olduğunda üssü büyük olan sayı daha büyüktür. Buna göre;

$\displaystyle {{2}^{{12}}}<{{2}^{{21}}}<{{2}^{{26}}}\text{ }\Rightarrow \text{ }c<a<b\text{ }$

Doğru Cevap : D şıkkı

SORU:17)

$\displaystyle \begin{array}{*{20}{l}} {a={{{\left( {\frac{2}{5}} \right)}}^{{35}}}} \\ {b={{{\left( {\frac{{125}}{8}} \right)}}^{{13}}}} \\ {c={{{\left( {\frac{4}{{25}}} \right)}}^{{17}}}} \end{array}$

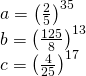
olduğuna göre, aşağıdaki sıralamalardan hangisi doğrudur?

ÇÖZÜM:

Sayıların tabanlarını aynı yapmaya çalışalım. Burdaki üslü sayıları $\displaystyle \frac{2}{5}$ tabanında ifade edebiliriz.

$\displaystyle \begin{array}{*{20}{l}} {a={{{\left( {\frac{2}{5}} \right)}}^{{35}}}} \\ {b={{{\left( {\frac{{125}}{8}} \right)}}^{{13}}}={{{\left( {\frac{8}{{125}}} \right)}}^{{-13}}}={{{\left[ {{{{\left( {\frac{2}{5}} \right)}}^{3}}} \right]}}^{{-13}}}={{{\left( {\frac{2}{5}} \right)}}^{{-39}}}} \\ {c={{{\left( {\frac{4}{{25}}} \right)}}^{{17}}}={{{\left[ {{{{\left( {\frac{2}{5}} \right)}}^{2}}} \right]}}^{{17}}}={{{\left( {\frac{2}{5}} \right)}}^{{34}}}} \end{array}$

Taban 0 ile 1 arasında olduğunda üssü büyük olan sayı daha küçüktür. Buna göre;

$\displaystyle {{\left( {\frac{2}{5}} \right)}^{{35}}}<{{\left( {\frac{2}{5}} \right)}^{{34}}}<{{\left( {\frac{2}{5}} \right)}^{{-39}}}\text{ }\Rightarrow \text{ a}<c<b$

Doğru Cevap : B şıkkı

SORU:18)

$\displaystyle \begin{array}{*{20}{l}} {a={{2}^{{200}}}} \\ {b={{3}^{{150}}}} \\ {c={{5}^{{100}}}} \end{array}$

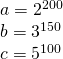
olduğuna göre, aşağıdaki sıralamalardan hangisi doğrudur?

ÇÖZÜM:

Sayıların tabanlarını aynı yapamayacağımız için üslerini aynı yapmaya çalışalım. Burdan yorumda bulunabiliriz. Üsleri 50 olacak şekilde sayıları dönüştürebiliriz.

$\displaystyle \begin{array}{*{20}{l}} {a={{2}^{{200}}}={{{({{2}^{4}})}}^{{50}}}={{{16}}^{{50}}}} \\ {b={{3}^{{150}}}={{{({{3}^{3}})}}^{{50}}}={{{27}}^{{50}}}} \\ {c={{5}^{{100}}}={{{({{5}^{2}})}}^{{50}}}={{{25}}^{{50}}}} \end{array}$

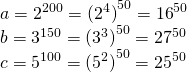
Üsler aynı olduğunda tabanı büyük olan sayı daha büyüktür. Buna göre;

$\displaystyle {{16}^{{50}}}<{{25}^{{50}}}<{{27}^{{50}}}\text{ }\Rightarrow \text{ a}<c<b$

Doğru Cevap : B şıkkı

Kitap Formatında Görmek için Tıkla

Soru ve Çözümleri (Latex Formatı)

“Soru ve Çözümleri (Latex Formatı)” üzerine bir yorum

Yorum yapın Cancel reply