Faiz Problemleri (Latex Formatı)

Çözüm için Tıklayınız

SORU 2

6400 lira 5 ayda 800 lira faiz getiriyorsa bankanın yıllık faiz oranı yüzde kaçtır?

A) 10 B) 15 C) 20 D) 25 E) 30

Çözüm için Tıklayınız

SORU 3

Yıllık %20 faiz oranı ile bankaya yatırılan bir miktar para 72 gün sonra faizi ile birlikte 2080 lira olduğuna göre, bankaya yatırılan para kaç liradır?

A) 1700 B) 1800 C) 1900 D) 2000 E) 2100

Çözüm için Tıklayınız

SORU 4

1000 liranın bir kısmı %20 den, geri kalanı da %30 dan basit faize yatırılıyor. İki yıl sonunda her ikisinden toplam 450 lira faiz alındığına göre %20 den faize verilen para kaç liradır?

A) 500 B) 600 C) 750 D) 800 E) 850

Çözüm için Tıklayınız

SORU 5

Ayşe,elindeki parayı yıllık %40 faiz veren bir bankaya 2 yıllığına yatırıyor. Eğer Ayşe, aynı süre için %30 faiz veren bir bankaya para yatırsaydı 300 lira daha az faiz alacaktı. Buna göre Ayşe’nin elindeki para kaç liradır?

A) 1000 B) 1200 C) 1400 D) 1500 E) 2000

Çözüm için Tıklayınız

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU 6

300 lira yıllık %30 dan 2 yıllığına bileşik faiz ile bankaya yatırılırsa kaç lira faiz getirir?

A) 170 B) 207 C) 220 D) 260 E) 300

Çözüm için Tıklayınız

SORU 7

Yıllık enflasyonun %10 olduğu bir dönemde %32 faizle bankaya yatırılan bir miktar para dönem sonunda gerçek değerinden yüzde kaç kazanç sağlamıştır?

A) 15 B) 16 C) 18 D) 20 E) 22

Çıkmış Sorular için Tıkla
Faiz Problemleri Çözümlü Soruları pdf indir

Çözüm için Tıklayınız

Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

Konu Anlatımı için Tıkla

Sadece Soruları pdf indir

Kitap Formatında Görmek için Tıkla

SORU ÇÖZÜMLERİ

ÇÖZÜM 7

Bankaya 100 lira para yatırıldığını varsayalım,
%32 faiz sonucu bu para 132 lira olacaktır.
%10 enflasyon olduğundan, 100 liranın değeri yıl sonunda 110 liraya denk olacaktır.
Buna göre gerçek kazanç =132 – 110 = 22 liradır.
Bu da yüzde olarak :
$\displaystyle \frac{{22}}{{110}}=\frac{x}{{100}}$
$\displaystyle \frac{1}{5}=\frac{x}{{100}}$
$\displaystyle 5x=100$
$\displaystyle x=20$ buluruz.
Doğru Cevap : D şıkkı

Çıkmış Sorular için Tıkla
Faiz Problemleri Çözümlü Soruları pdf indir

Konu Anlatımı için Tıkla

Sadece Soruları pdf indir

Kitap Formatında Görmek için Tıkla

ÇÖZÜM 6

Bileşik faiz demek, her yılın sonunda elde edilen faiz anaparaya eklenerek, yeniden faiz hesabında tüm paranın hesap edilmesi demektir.
Bileşik faiz hesabında şu formülden yararlanılır,
$\displaystyle A+F=A\cdot {{\left( {1+\frac{n}{{100}}} \right)}^{t}}$
(A: Anapara, F:Faiz, n: Faiz Yüzdesi, t : süre)
Buna göre,
$\displaystyle 300+F=300\cdot {{\left( {1+\frac{{30}}{{100}}} \right)}^{2}}$
$\displaystyle 300+F=300\cdot {{\left( {\frac{{130}}{{100}}} \right)}^{2}}$
$\displaystyle 300+F=300\cdot \frac{{130}}{{100}}\cdot \frac{{130}}{{100}}$
$\displaystyle 300+F=3.13.13$
$\displaystyle 300+F=507$
$\displaystyle F=507-300$
$\displaystyle F=207$ lira bulunur.
Doğru Cevap : B şıkkı

ÇÖZÜM 5

Ayşe’nin elindeki paraya x diyelim. Buna göre iki faiz arasındaki farkı denklem halinde yazalım.
$\displaystyle \frac{{x.40.2}}{{100}}-\frac{{x.30.2}}{{100}}=300$
$\displaystyle \frac{{80x-60x}}{{100}}=300$
$\displaystyle \frac{{20x}}{{100}}=300$
$\displaystyle \frac{x}{5}=300$
$\displaystyle x=1500$
Doğru Cevap : D şıkkı

ÇÖZÜM 4

%20 den faize yatırılan paraya x dersek,
kalan kısım 1000-x olur. Buna göre faizler toplamını denklem halinde yazalım.
$\displaystyle \frac{{x.20.2}}{{100}}+\frac{{(1000-x).30.2}}{{100}}=450$
$\displaystyle \frac{{40x+60000-60x}}{{100}}=450$
$\displaystyle 60000-20x=45000$
$\displaystyle 20x=15000$
$\displaystyle x=750$ lira olarak buluruz.
Doğru Cevap : C şıkkı

ÇÖZÜM 3

1 yılda 12 ay ve her ayda 30 gün olduğu kabul edildiği için, günlük faiz hesabında normal faiz formülünün paydasına 12 ve 30 çarpanı gelir.
Günlük faiz formülü;
$\displaystyle F=\frac{{A.n.t}}{{100.12.30}}$ şeklindedir.
(A: Anapara, n: faiz yüzdesi, t : süre(gün) )
Soruda faizi ile birlikte toplam paranın kaç olduğu verilmiş. Buna göre denklemi kuralım,
$\displaystyle A+F=2080$
$\displaystyle A+\frac{{A.n.t}}{{100.12.30}}=2080$
$\displaystyle A+\frac{{A.20.72}}{{100.12.30}}=2080$
$\displaystyle A+\frac{A}{{25}}=2080$
$\displaystyle \underset{{(25)}}{\mathop{{\frac{A}{1}}}}\,+\underset{{(1)}}{\mathop{{\frac{A}{{25}}}}}\,=2080$
$\displaystyle \frac{{26A}}{{25}}=2080$
$\displaystyle \frac{A}{{25}}=80$
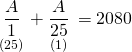
$\displaystyle A=25.80=2000$ lira buluruz.
Doğru Cevap : D şıkkı

ÇÖZÜM 2

1 yılda 12 ay olduğu için, Aylık faiz hesabında normal faiz formülünün paydasına 12 çarpanı gelir. Aylık faiz formülü;
$\displaystyle F=\frac{{A.n.t}}{{100.12}}$
şeklindedir.
(A: Anapara, n: faiz yüzdesi, t : süre(ay) )
Soruda verilenleri, formülde yerine yerleştirelim
$\displaystyle 800=\frac{{6400.n.5}}{{100.12}}$
$\displaystyle 800=\frac{{64.n.5}}{{1.12}}$
$\displaystyle 800=\frac{{16.n.5}}{3}\Rightarrow 800=\frac{{80.n}}{3}$
$\displaystyle 10=\frac{{1.n}}{3}\Rightarrow n=30$ buluruz.
Doğru Cevap : E şıkkı

ÇÖZÜM 1

Yıllık faiz şu formülle hesaplanır,
$\displaystyle F=\frac{{A.n.t}}{{100}}$
(A: Anapara, n: faiz yüzdesi, t : süre)
Soruda verilenleri, formülde yerine yerleştirelim
$\displaystyle F=\frac{{2000.30.3}}{{100}}=\frac{{200.3.3}}{1}=1800$ lira buluruz.
Doğru Cevap : B şıkkı