Basit Eşitsizlikler (Latex Formatı)

Bu bölümde Basit Eşitsizlikler ile ilgili 24 adet soru bulunmaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…


SORULAR

SORU 1


Sayı doğrusu üzerinde taralı bölge aşağıdakilerden hangisi ya da hangileri ile ifade edilebilir?
I. x < 2 ve x ≥ 5
II. x ∈ R \ (-2,5]
III. x ∈ (-∞, 2) U [5,∞)

A) Yalnız I    B) Yalnız II    C) I ve II    

D) II ve III    E) I ve III

Doğru Cevap Çözüm için Tıklayınız

SORU 2

x ∈ [ 5, 1) ∪ [1,4) ifadesini sağlayan x tam sayıların toplamı kaçtır?

A) -9   B) -8   C) -5   D) -3   E) 0

Doğru Cevap Çözüm için Tıklayınız

SORU 3

x bir reel sayı olmak üzere,

\displaystyle \frac{{2x-1}}{3}<3x-5
eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?

A) (1,∞)    B) (2,∞ )     C) (3,∞ )     D) (1,2)     E) (2,3)

Doğru Cevap Çözüm için Tıklayınız

SORU 4

x bir reel sayı olmak üzere,

\displaystyle \frac{{3x-1}}{4}<\frac{{2x-5}}{3}
eşitsizliğini sağlayan x değerlerinin kümesi aşağıdakilerden hangisidir?

A) (-17,∞)    B) [-17,∞)    C) (-∞,-17)    

D) (-∞,17)    E) (-∞ ,-17)

Doğru Cevap Çözüm için Tıklayınız

SORU 5

x bir reel sayı olmak üzere,

\displaystyle -5x-1\ge \frac{13}{3}
eşitsizliğinin çözüm kümesinin sayı doğrusu üzerinde gösterilmiş hali, aşağıdaki seçeneklerden hangisinde doğru gösterilmiştir?

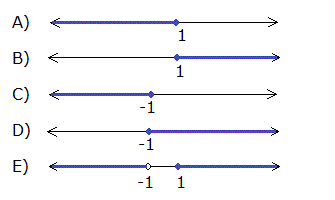
Doğru Cevap Çözüm için Tıklayınız

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU 6

x bir reel sayı olmak üzere,

\displaystyle \frac{{x-1}}{3}-\frac{{x+2}}{4}<3
eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?

A) (-∞,46]    B) [-46,∞)    C) (-∞,46)   

D) (-∞ ,-46]    E) (-∞, -46)

Doğru Cevap Çözüm için Tıklayınız

SORU 7

\displaystyle \frac{x}{3}-2\ge \frac{{2x}}{5}+2
eşitsizliğini sağlayan en büyük x tam sayısı kaçtır?

A) -61   B) -60   C) -59   D) -58   E) -57

Doğru Cevap Çözüm için Tıklayınız

SORU 8

Kerem, A ve B şirketleriyle iş görüşmesine gidiyor. A şirketi \frac{2x}{3} lira maaş ve 500 lira prim teklif ediyor. B şirketi ise \frac{x}{2} lira maaş ve yıllık 3x lira ikramiye teklif ediyor. Kerem, hem maaş hem de yol yakınlığı gerekçesiyle B şirketini seçiyor. Buna
göre, x en az kaçtır?

A) 4000 B) 4500 C) 5000 D) 5500 E) 6000

Doğru Cevap Çözüm için Tıklayınız

SORU 9

Hülya’nın yaşı 3x – 2, küçük kardeşi Berk’in yaşı x + 6 ve abisi Selim’in yaşı 2x + 7 olduğuna göre, x’in değer aralığı kaçtır?

A) (4,9) B) (5,7) C) (5,8) D) (5,9) E) (6,9)

Doğru Cevap Çözüm için Tıklayınız

SORU 10

-7 < 2x – 1 ≤ 5
olduğuna göre \frac{x}{3}+2 ifadesinin alabileceği tam sayı değerlerinin toplamı kaçtır?

A) 3   B) 4    C) 5    D) 6    E) 7

Doğru Cevap Çözüm için Tıklayınız

SORU 11

-7 < 2x – 1 < 17 ve 3x + 2y + 1 = 0
olduğuna göre, y nin alabileceği kaç farklı x tam sayı değeri var dır?

A) 14 B) 15 C) 16 D) 17 E) 18

Doğru Cevap Çözüm için Tıklayınız

SORU 12

3x – 5 ≤ 4x + 2 ≤ x + 14

eşitsizliğini sağlayan x değerlerinin çözüm aralığı aşağıdakilerden hangisidir?

A) [ -7,4]     B) ( -7,4]     C) [ -7,4)    

D) (- 7,4)     E) (-4, 7)

Doğru Cevap Çözüm için Tıklayınız

SORU 13

x – 3 < 2y + 1 < 3x + 15

eşitsizliğini sağlayan en küçük x tam sayı değeri için y nin değer aralığı aşağıdakilerden hangisidir?

A) [ -7,4)    B) [ -7,4]    C) ( -5, 4)    

D) [ -5, -4)    E) ( -5, -4]

Doğru Cevap Çözüm için Tıklayınız

SORU 14

\displaystyle \frac{1}{{12}}<\frac{1}{{x+3}}<\frac{1}{6}

olduğuna göre, x in alabileceği en küçük ve en büyük tam sayı değerlerinin toplamı kaçtır?

A) 10 B) 12 C) 13 D) 14 E) 15

Doğru Cevap Çözüm için Tıklayınız

SORU 15

0 < y < x olmak üzere,

\displaystyle y.z=3x+5y
eşitliğini sağlayan z değerleri için aşağıdakilerden hangisi doğrudur?
A) z < 3       B) 3 < z < 5      C) 3 < z < 8    D) z < 8     E) z > 8

Doğru Cevap Çözüm için Tıklayınız

SORU 16

x < y < 0 < z
olduğuna göre, aşağıdakilerden hangisi yanlıştır?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }x.z<0\text{ }} & {B)\text{ }x-z<0} & {C)\text{ }x.y.z<0} \end{array}
\displaystyle \begin{array}{*{20}{c}} {\text{ }D)\text{ }\frac{{x.y}}{z}>0} & {E)\text{ }z-y>0} \end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 17

a + c < b + c
a.c < b.c
olduğuna göre, aşağıdakilerden hangisi kesinlikle yanlıştır?

A) a > 0    B) b < 0     C) a – b < 0  

D) a ^{b} > 0 E) b – a + c < 0

Doğru Cevap Çözüm için Tıklayınız

SORU 18

a.b.c < 0
a.b² > 0
a.c < 0
olduğuna göre, a,b ve c nin işaretleri sırasıyla aşağıdakilerden hangisi olabilir?
A) +,+,-       B) +,-,+        C) -,+,+        

D) +,+,+      E) -,-,-

Doğru Cevap Çözüm için Tıklayınız

SORU 19

a² < a olmak üzere,
4a + 3
ifadesinin alabileceği tam sayı değerlerinin toplamı kaçtır?

A) 9     B) 13     C) 14     D) 15        E) 16

Doğru Cevap Çözüm için Tıklayınız

SORU 20

a < a² < |a|
b³ < b < b² olmak üzere, aşağıdaki ifadelerden hangisi kesinlikle doğrudur?

A) a – b < -1      B) a + b <  1         C)  a < 1
D) b > 1        E) a + b > -1

Doğru Cevap Çözüm için Tıklayınız

SORU 21

x ve y birer reel sayıdır.
2 < x ≤ 4
-5 ≤ y < 1
olduğuna göre, 4x – y ifadesinin alabileceği kaç farklı tam sayı değeri var dır?

A) 4    B) 8     C) 12     D) 14     E) 18

Doğru Cevap Çözüm için Tıklayınız

SORU 22

2 < x < 4
-5 < y < 1

olduğuna göre, x.y ifadesinin değer aralığı aşağıdakilerden hangisidir?

A) (-10,4)      B) (-20,4)      C) (2,4)
D) (-2,4)      E) (-20,10)

Doğru Cevap Çözüm için Tıklayınız

SORU 23

-3 < x ≤ 4
olduğuna göre x² + 1 ifadesinin alabileceği en büyük tam sayı değeri ile en küçük tam sayı değerinin toplamı kaçtır?

A) 11    B) 15    C) 18    D) 22      E) 27

Doğru Cevap Çözüm için Tıklayınız

SORU 24

x ve y birer gerçel sayıdır.
-3 < x < 3
-2 < y < 2
olduğuna göre, x³ + y³ ifadesinin alabileceği en büyük tam sayı değeri kaçtır?

A) 13     B) 15     C) 27     D) 34       E) 54

Doğru Cevap Çözüm için Tıklayınız
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU ÇÖZÜMLERİ

ÇÖZÜM 24

\displaystyle -3<x<3\text{ }\Rightarrow \text{ }-27<{{x}^{3}}<27

\displaystyle -2<y<2\text{ }\Rightarrow \underline{{\text{ }\underset{+}{\mathop{{}}}\,\text{ }-8<{{y}^{3}}<8\text{ }}}

\displaystyle \text{ }-35<{{x}^{3}}+{{y}^{3}}<35

Buna göre en büyük tam sayı değeri 34 olur.

Doğru Cevap : D şıkkı

Soruyu Gör
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
 

ÇÖZÜM 23

\displaystyle -3<x\le 4

x = 0 değerini alabildiği için x² en az 0 olabilir.
x, mutlak değerce en fazla 4 olabildiği için x² en fazla 16 olabilir.
Buna göre;

\displaystyle 0\le {{x}^{2}}\le 16
\displaystyle 1\le {{x}^{2}}+1\le 17

Buna göre en az 1, en çok 17 değeri olabilir.
Toplamları: 1 + 17 = 18 buluruz.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 22

x.y çarpımının sınır değerlerini bulmak için tüm sınır değerlerini çarparız.

\displaystyle \left. \begin{array}{l}\text{ }2<x<4\\-5<y<1\end{array} \right\}\text{ }\begin{array}{*{20}{c}} {\Rightarrow 2.(-5)=-10} & {2.1=2} \\ {\Rightarrow 4.(-5)=-20} & {4.1=4} \end{array}

Bulduğumuz maximum değer ile minimum değer bize aralığı verir. Buna göre;
\displaystyle -20<x.y<4

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 21

4x – y nin hangi değerler arasında bulmak için 4x’in değer aralığı ile -y nin aralığını toplamalıyız.

\displaystyle 2<x\le 4 (Her tarafı 4 ile çarpalım)
\displaystyle 8<4x\le 16
\displaystyle -5\le y<1 (Her tarafı 1 ile çarpalım)
\displaystyle -1<-y<5

\displaystyle \text{ }8<4x\le 16
\displaystyle \underline{{\text{ }\underset{+}{\mathop{{}}}\,\text{ }-5<-y\le 1\text{ }}}
\displaystyle \text{ }3<4x-y\le 17
4x – y  nin alacağı değerler : 4,5,…,17
\displaystyle \Rightarrow  14 değer alabilir.

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 20

\displaystyle a<{{a}^{2}}<\left| a \right|\text{ }\Rightarrow Bu eşitsizliğin sağlanması için a, -1 ile 0 arasında olmak zorundadır.
\displaystyle {{b}^{3}}<b<{{b}^{2}}\text{ }\Rightarrow Bu eşitsizliğin sağlanması için b, -1 den küçük olmak zorundadır.
Buna göre; \displaystyle -1<a<0
\displaystyle \text{ }b<-1
\displaystyle a<0\text{ }ve\text{ }b<-1 şartlarına göre
\displaystyle a+b<0+(-1)\text{ }\Rightarrow \text{ }a+b<-1 olmak zorundadır.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 19

Sadece 0 ile 1 arasındaki sayıların karesi kendisinden küçüktür.
\displaystyle {{a}^{2}}<a\text{ }\Rightarrow \text{ }0<a<1 dir.
\displaystyle 0<a<1 (Her tarafı 4 ile çarpalım)
\displaystyle 0<4a<4 (Her tarafa 3 ekleyelim)
\displaystyle 3<4a+3<7
Buna göre \displaystyle 4a+3\text{ }:\text{ }4,5,6 değerlerini alabilir.
Toplam: \displaystyle 4+5+6=15 bulunur.

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 18

\displaystyle a.{{b}^{2}}>0\text{ }\Rightarrow \text{ }{{b}^{2}} pozitiftir; buna göre a pozitiftir.
\displaystyle a.c<0\text{ }\Rightarrow a ile c zıt işaretlidir. a pozitif ise; c
negatiftir.
\displaystyle a.b.c<0\text{ }\Rightarrow a pozitif ve c negatifti. Çarpımın
negatif olması için b pozitif olmalıdır.
Buna göre işaretler :\displaystyle +,+,- dir.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 17

\displaystyle a+c<b+c\text{ }\Rightarrow \text{ }a<b dir.
\displaystyle \text{ }a.c<b.c\text{ }\Rightarrow \text{ }a<b eşitsizliğinin her iki tarafı c ile çarpılmış ve eşitsizlik yön değiştirmemiş.
Buna göre; c > 0 dır.
A) \displaystyle a>0\text{ }\Rightarrow kesinlikle yanlış olduğunu bilemeyiz.
B) \displaystyle b<0\text{ }\Rightarrow kesinlikle yanlış olduğunu bilemeyiz.
C) \displaystyle \text{a}-b<0\Rightarrow a, b den küçüktü. Kesinlikle doğru
D) \displaystyle {{\text{a}}^{b}}>0\text{ }\Rightarrow kesinlikle yanlış olduğunu bilemeyiz.
E) \displaystyle \text{b}-a+c<0\text{ }\Rightarrow \text{ (b}-a) pozitiftir, c de pozitif idi. Bu ikisinin toplamı 0 dan büyüktür. Kesinlikle yanlış olan şık budur.

Doğru Cevap: E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 16

\displaystyle x<y<0<z ise x ve y negatif (-) işaretli; z ise pozitif ( +) işaretlidir.
A) \displaystyle x.z<0\text{ }\Rightarrow \text{ }(-).(+)=(-) dir. Doğru
B) \displaystyle x-z<0\text{ }\Rightarrow \text{ }(-)-(+)=(-) dir. Doğru
C) \displaystyle x.y.z<0\text{ }\Rightarrow \text{ }(-).(-).(+)=(+) dır. Yanlış
D) \frac{x.y}{z}>0 \displaystyle \Rightarrow \text{ }(-).(-)/(+)=(+) dır. Doğru
E) \displaystyle z-y>0\text{ }\Rightarrow (+)-(-)=(+)+(+)=+ dır. Doğru

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 15

\displaystyle y.z=3x+5y eşitliğinde her tarafı y’ ye bölersek;
\displaystyle z=\frac{{3x}}{y}+5 olur.
\displaystyle 0<y<x eşitsizliğinde her tarafı y e bölelim.
\displaystyle \frac{0}{y}<\frac{y}{y}<\frac{x}{y}\text{ }\Rightarrow 0<1<\frac{x}{y}\text{ }(\text{ }3\text{ }ile\text{ c}arpal\imath m)
\displaystyle 0<3<\frac{{3x}}{y}\text{ }\Rightarrow \text{ }(Her\text{ }tarafa\text{ }5\text{ }ekleye\lim )
\displaystyle 5<8<\frac{{3x}}{y}+5\text{ }\Rightarrow 8<z\text{ }\Rightarrow z>8\text{ }d\imath r.

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 14

\displaystyle \frac{1}{{12}}<\frac{1}{{x+3}}<\frac{1}{6}
eşitsizlikteki kesirleri ters çevirirsek eşitsizlik yön değiştirir.
\displaystyle \frac{{12}}{1}>\frac{{x+3}}{1}>\frac{6}{1}\text{ }\Rightarrow \text{ }12>x+3>6
\displaystyle 12-3>x>6-3\text{ }\Rightarrow \text{ }9>x>3

Buna göre x’in en büyük tam sayı değeri 8 , en küçük tam sayı değeri 4 tür. Bunların toplamı da 8 + 4 = 12 bulunur.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 13

\displaystyle \underbrace{{x-3}}_{\searrow }<2y+1<\underbrace{{3x+15}}_{\swarrow }
\displaystyle \text{ }x-3<3x+15
\displaystyle x-3x<18
\displaystyle -2x<18
\displaystyle -x<9
\displaystyle x>-9\text{ }\Rightarrow x in en küçük tam sayı değeri 8 dir.

\displaystyle x-3<2y+1<3x+15\text{ }\Rightarrow \text{ }-11<2y+1<-9
\displaystyle -10<2y<-8
\displaystyle -5<y<-4\text{ }\Rightarrow \text{ (}-5,-4)

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 12

\displaystyle x-3<2y+1<3x+15 eşitsizliğindeki x değerlerini bulmak için 2 parça halinde inceleyelim.

1.durum:
\displaystyle \underbrace{{3x-5\le 4x+2}}_{{Buraya\text{ }bakal\imath m}}\le x+14
\displaystyle 3x-5\le 4x+2
\displaystyle -x\le 2+5
\displaystyle -x\le 7
\displaystyle x\ge -7

2.durum:
\displaystyle 3x-5\le \underbrace{{4x+2\le x+14}}_{{Buraya\text{ }bakal\imath m}}
\displaystyle 4x+2\le x+14
\displaystyle 3x\le 12
\displaystyle x\le 4

Bu iki duruma göre Ç.K: [-7,4] tür.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 11

İlk önce x’in değer aralığını bulalım.
\displaystyle -7<2x-1\le 17\text{ }(Her\text{ }tarafa\text{ }1\text{ }ekleye\lim )
\displaystyle -6<2x\le 18\text{ }(Her\text{ }tarafa\text{ }2\text{ }ye\text{ }b\ddot{o}le\lim )
\displaystyle -3<x\le 9

\displaystyle 3x+2y+1=0 eşitliğinde x’i y cinsinden yazalım.
\displaystyle 3x=-2y-1
\displaystyle x=\frac{{-2y-1}}{3}

Bunu x’in değer aralığına yazalım.

\displaystyle -3<x\le 9\text{ }\Rightarrow \text{ }-3<\frac{{-2y-1}}{3}\le 9
\displaystyle -9<-2y-1\le 27
\displaystyle -8<-2y\le 28
\displaystyle -4<-y\le 14
\displaystyle 4>y\ge -14

Buna göre; y, -14 ten 3 e kadar tüm tam sayı değerlerini alabilir.
\displaystyle Terim\text{ }Say\imath s\imath \text{ }=\text{ }\frac{{Son\text{ }Terim-\dot{I}lk\text{ }Terim}}{{Art\imath s\text{ }Miktar\imath }}+1
\displaystyle =\frac{{3-(-14)}}{1}+1=18\text{ buluruz}\text{.}

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 10

İlk önce x’in değer aralığını bulalım.
\displaystyle -7<2x-1\le 5 (Her tarafa 1 ekleyelim)
\displaystyle -6<2x\le 6 (Her tarafı 2 ye bölelim)
\displaystyle -3<x\le 3 buluruz.

Şimdi \frac{x}{3}+2 nin değer aralığını bulalım.
\displaystyle -3<x\le 3   (Her tarafı 3 e bölelim)
\displaystyle -1<\frac{x}{3}\le 1  (Her tarafa 2 ekleyelim)
\displaystyle 1<\frac{x}{3}+2\le 3\text{ }\Rightarrow Bu ifade 2 ve 3 değerlerini alabilir. Toplam: 2 + 3 = 5 buluruz.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 9

\displaystyle \begin{array}{*{20}{l}} \begin{array}{l}x+6<3x-2\text{ }olmal\imath \\\text{ }8<2x\\\text{ }4<x\end{array} & \begin{array}{l}3x-2<2x+7\text{ }olmal\imath \\3x-2x<7+2\\\text{ }x<9\end{array} \end{array}

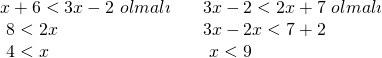
Bu iki duruma göre;
\displaystyle 4<x<9 yani \displaystyle x\in (4,9) dur.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 8

A şirketinin verdiği para, B şirketinin verdiği paradan fazla olamaz.
B şirketinin teklifindeki yıllık ikramiye 3x idi.

Bunu aylık olarak düşünürsek : \frac{3x}{2} olur.
A şirketinin teklifi ≤ B şirketinin teklifi
\displaystyle \underset{{(4)}}{\mathop{{\frac{{2x}}{3}}}}\,+500\le \underset{{(6)}}{\mathop{{\frac{x}{2}}}}\,+\frac{{3x}}{{12}}
\displaystyle \frac{{8x}}{{12}}+500\le \frac{{6x+3x}}{{12}}
\displaystyle \frac{{8x}}{{12}}+500\le \frac{{9x}}{{12}}
\displaystyle 500\le \frac{x}{{12}}
\displaystyle 6000\le x
\displaystyle x\ge 6000

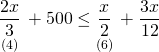
Buna göre, x en az 6000 lira olmak zorundadır.

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 7

\displaystyle \frac{x}{3}-2\ge \frac{{2x}}{5}+2
\displaystyle \underset{{(5)}}{\mathop{{\frac{x}{3}}}}\,-\underset{{(3)}}{\mathop{{\frac{{2x}}{5}}}}\,\ge 2+2
\displaystyle \frac{{5x-6x}}{{15}}\ge 4
\displaystyle \frac{{-x}}{{15}}\ge 4
\displaystyle -x\ge 60
\displaystyle x\le -60

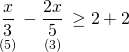
Bu koşulu sağlayan en büyük x tam sayısı -60 tır.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 6

Paydaları eşitleyerek çözüme başlayalım.
\displaystyle \underset{{(4)}}{\mathop{{\frac{{x-1}}{3}}}}\,-\underset{{(3)}}{\mathop{{\frac{{x+2}}{4}}}}\,<3
\displaystyle \frac{{4x-4}}{{12}}-\frac{{3x+6}}{{12}}<3
\displaystyle \frac{{4x-4-3x-6}}{{12}}<3
\displaystyle \frac{{x-10}}{{12}}<3
\displaystyle x-10<36
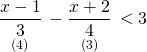
\displaystyle x<46 buluruz.
Buna göre; Çözüm Kümesi: (-∞,46) dır.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 5

İçler dışlar çarpımı yaparak çözüme başlayalım.
\displaystyle -5x-\frac{2}{3}\ge \frac{{13}}{3}
\displaystyle -15x-2\ge 13
\displaystyle -15x\ge 15
\displaystyle -x\ge 1
\displaystyle x\le -1 buluruz.

Bunu da sayı doğru üzerinde -∞ dan -1’e kadar olan alandır. Bu alana da -1 dahildir.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 4

İçler dışlar çarpımı yaparak çözüme başlayalım.

\displaystyle \frac{{3x-1}}{4}<\frac{{2x-5}}{3}
\displaystyle 9x-3<8x-20
\displaystyle x<-17

Çözüm Kümesi: (-17,∞)

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 3

İçler dışlar çarpımı yaparak çözüme başlayalım.
\displaystyle \frac{{2x-1}}{3}<3x-5
\displaystyle 2x-1<9x-15
\displaystyle -7x<-14
\displaystyle -x<-2 (iki taraf da – ile çarpılırsa eşitlik yön değiştirir.)
\displaystyle x>2
Çözüm Kümesi: (2,∞)

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 2

\displaystyle [-5,-1)\text{ }\Rightarrow \text{ }-5,-4,-3,-2 tam sayıları var dır.
\displaystyle [1,4)\text{ }\Rightarrow \text{ }1,2,3 tam sayıları var dır.
Bu tam sayıların toplamı:
\displaystyle \left( {-5} \right)+\left( {-4} \right)+\left( {-3} \right)+\left( {-2} \right)+1+2+3=-8 bulunur

Doğru Cevap: B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 1

Sayı doğrusuna baktığımızda -∞ dan -2 ye kadar olan bölgenin tarandığını ve -2’nin buna dahil edilmediğini görüyoruz.
Burasını x < -2 veya (-∞,-2) şeklinde ifade edebiliriz.
İkinci olarak da 5 dahil, 5’ten sonsuza kadar olan bölgenin tarandığını görüyoruz.
Burasını da x ≥ 5 veya [5,∞) şeklinde ifade edebiliriz.
Buna göre;
I. x < -2 ve x ≥ 5 ⇒ doğru
II. x ∈ R \ (-2,5] ⇒ Tüm reel sayılardan [-2,5) aralığı çıkarılmalıydı ⇒ yanlış
III. x (-∞, 2) U [5,∞) ⇒ doğru

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
 

Yorum yapın