Basit Eşitsizlikler Konu Anlatımı

$a$ sayısı $b$ sayısına eşit değilse $\displaystyle a\ne b$ şeklinde gösterilir.

$a$ büyüktür $b$ den ise $a>b$ şeklinde,

$a$ küçüktür $b$ den ise $a<b$ şeklinde gösterilir.

Örnek:

$3<5$

$7>2$

ARALIK

Kapalı Aralık

$[a,\text{ }b]\text{ }veya\text{ }a\le x\le b$ şeklinde gösterilen aralıklara kapalı aralık denir. Kapalı aralık da sınır değerler de dahildir.

Örnek:

$[-5,\text{ 7}]$ aralığı

Açık Aralık

$\displaystyle (a,\text{ }b)\text{ }veya\text{ }a<x<b$ şeklinde gösterilen aralıklara açıkı aralık denir. Yani uç noktalar dahil değildir.

Örnek:

$\displaystyle (-2,\text{ 5)}$ aralığı

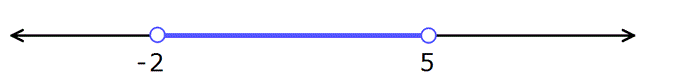
Yarı Açık Aralık

$\displaystyle (a,\text{ }b]\text{ veya }\!\![\!\!\text{ a}\text{, b)}$ şeklinde uç noktalardan biri dahil olup, diğeri dahil değilse bunlara yarı açık veya yarı kapalı aralık denir.

Örnek:

$[1,\text{ 8)}$ aralığı

Sınırsız Aralık

Bir ya da iki ucu sonsuza kadar giden aralıklardır.

Örnek:

$[1,\text{ }\infty \text{)}$ aralığı

Örnek:

$(-\infty ,\text{ 3)}$ aralığı

Örnek:

$(-\infty ,\text{ }\infty \text{)}$ aralığı

Örnek:

$(-2,\text{ 5 }\!\!]\!\!\text{ }$ aralığında kaç tam sayı vardır?

Çözüm:

$-2\text{ dahil de }\!\!\breve{\mathrm{g}}\!\!\text{ ildir}\text{.}$

$\Rightarrow \text{ }-1,\text{ 0}\text{, 1}\text{, 2}\text{, 3}\text{, 4}\text{, 5 }\Rightarrow \text{ 7 tane tam say }\!\!\imath\!\!\text{ vard }\!\!\imath\!\!\text{ r}\text{.}$

Basit Eşitsizlikler

$a\ne 0$ olmak üzere, $ax+b<0\text{ },\text{ }ax+b\le 0$ gibi ifadelere birinci dereceden bir bilinmeyenli eşitsizlikler denir.

ÖZELLİKLER

1. Her iki tarafa aynı sayıyı ekleyebilir, iki taraftan da aynı sayıyı çıkarılabiliriz.

Örnek:

$\displaystyle a<b\text{ }ise\text{ }a+3<b+3\text{ }t\ddot{u}r.$

$\displaystyle a<b\text{ }ise\text{ }a-5<b-5\text{ }tir.$

2.Her iki tarafı aynı pozitif sayı ile çarpabilir, aynı pozitif sayıya bölebiliriz.

Sayı negatif olursa eşitsizlik yön değişitirir.

Örnek:

$a<b\text{ }ise\text{ }a.5<b.5\text{ }tir.$

$a<b\text{ }ise\text{ }\frac{a}{8}<\frac{b}{8}\text{ }dir.$

$a<b\text{ }ise\text{ }-3.a>-3.b\text{ }dir.$

$a<b\text{ }ise\text{ }\frac{a}{{-2}}>\frac{b}{{-2}}\text{ }dir.$

3.Aynı sayıya bağlı eşitsizliklerden diğer sayıları kıyaslayabiliriz.

Örnek:

$a<3\text{ }ve\text{ }3<b\text{ }ise\text{ }a<b\text{ }dir.$

4.Aynı yönlü eşitsizlikler taraf tarafa toplanabilir.

Örnek:

$\displaystyle a<2\text{ }ve\text{ }b<3\text{ }ise\text{ }a+b<5\text{ }tir.$

5.Eşitsizliğin iki tarafı da aynı işaretli ise, takla attırmak eşitsizliğe yön değiştittirir.

Örnek:

$2<3\text{ }ise\text{ }\frac{1}{2}>\frac{1}{3}\text{ }t\ddot{u}r.$

$-5<-2\text{ }ise\text{ }-\frac{1}{5}>-\frac{1}{2}\text{ }dir.$

6. 0 ile 1 arasındaki sayıların pozitif tam sayı kuvvetini aldıkça sayı daha da küçülür.

Örnek:

$\displaystyle {{\left( {\frac{1}{2}} \right)}^{2}}<\frac{1}{2}\text{ dir}\text{.}$

Örnek Soru:

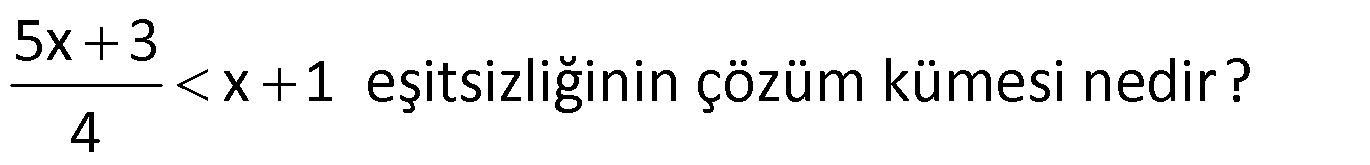
Çözüm:

Örnek Soru:

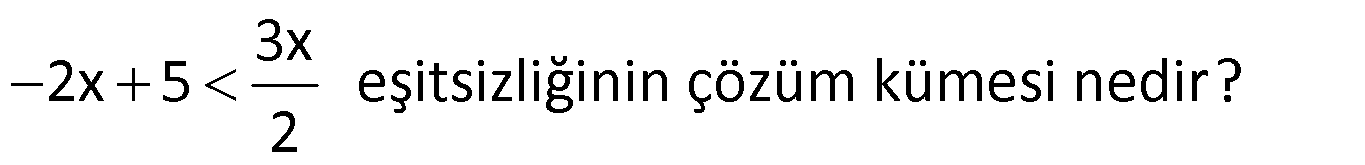
Çözüm:

Örnek Soru:

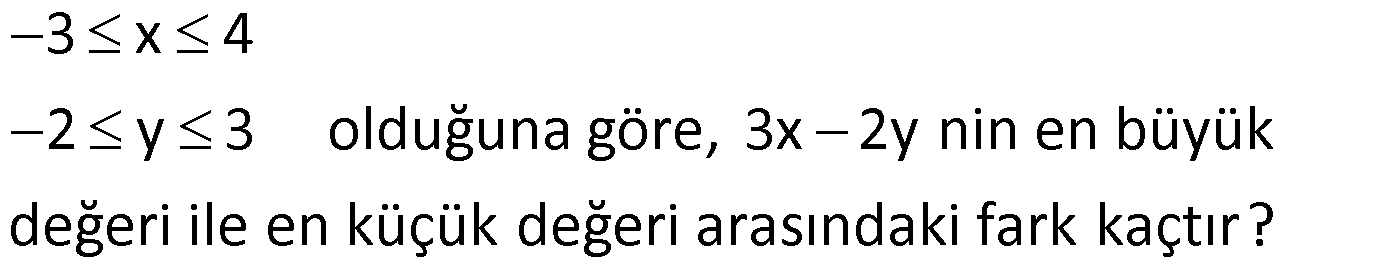
Çözüm:

1.Dereceden İki Bilinmeyenli Eşitsizlikler

$ax+by+c>0$

$ax+by+c\ge 0$

$ax+by+c<0$

$ax+by+c\le 0$

şeklinde yazılan ifadelere birinci dereceden iki bilinmeyenli eşitsizlik denir.

Bu eşitsizliklerden birden fazla bulunursa, bu gruba birinci dereceden iki bilinmeyenli eşitsizlik sistemi denir.

Çözüm kümesi analitik düzlemde taralı olarak gösterilir.

Örnek:

Çözüm:

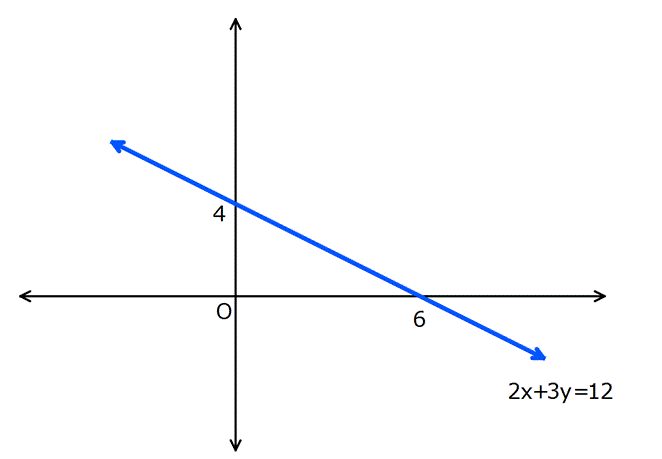
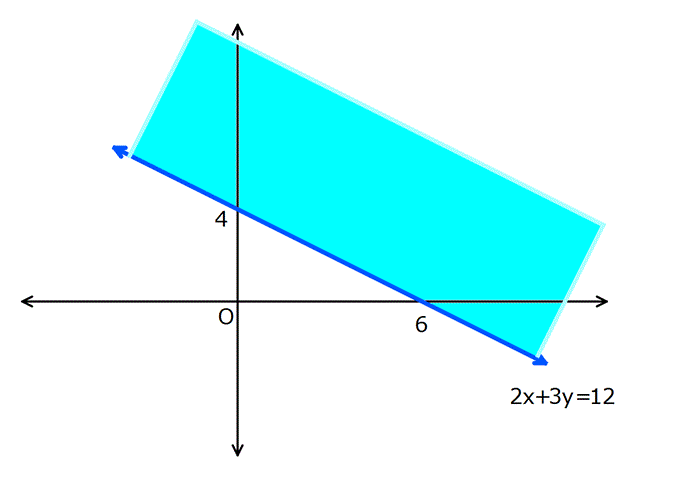
Örnek:

Çözüm:

Konu Anlatımını pdf indir

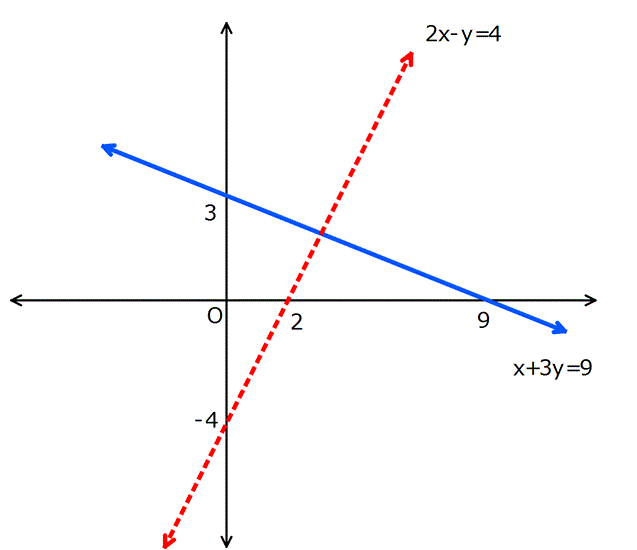
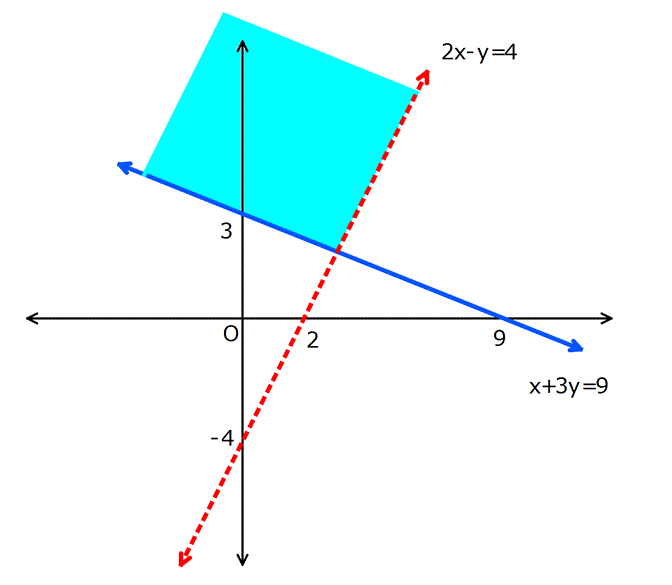
Çözümlü Sorular veya Daha Fazlası için Tıkla

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)