Soru Sor sayfası kullanılarak Limit konusu altında Parçalı fonksiyonlarda limit, limitin varlığı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
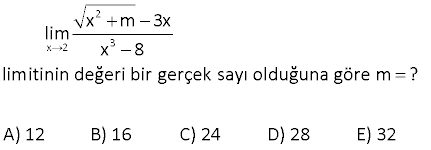

3.SORU

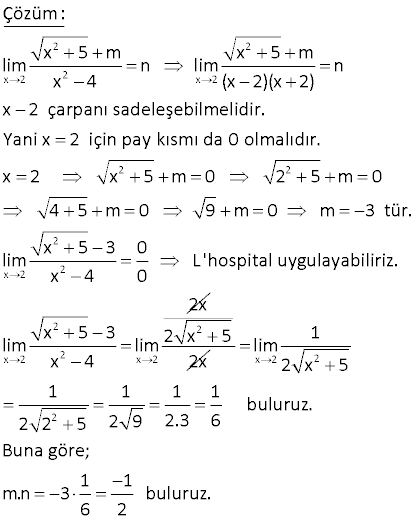
4.SORU


5.SORU
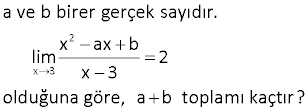

6.SORU

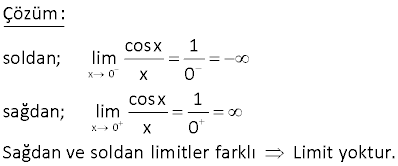
7.SORU


8.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
3 x , x 1 f(x) x 2 , x 1 fonksiyonunun x 1 noktasındaki limitini bulunuz. x 1 2 2 x 1 Çözüm: Sağdan ve soldan limitlerine bakalım. lim x 2 1 2 1 lim x 1 1 Sağdan ve soldan limiti aynı olduğu için x 1 noktasında limiti var dır ve 1’e eşittir. Cevap: 1 3 2 x 2 3 x m 3x lim x 8 limitinin değeri bir gerçek sayı olduğuna göre m ? A) 12 B) 16 C) 24 D) 28 E) 32 www.matematikkolay.net 2 x 2 3 2 x 2 3 2 x 2 2 2 Çözüm: x m 3x lim c R olsun. x 8 x m 3x lim ifadesinde limitin gerçek sayı olması x 8 için paydayı 0′ yapan ifadenin sadeleşmesi lazım. x m 3x lim x 2 x 2x 4 x m 3x ile x 2 sadeleşmeli. Yani ifa 2 de x 2 ye tam bölünmeli x 2 0 x 2 dir 2 m 3.2 0 m 4 6 m 4 36 m 32 bulunur. 33 2 x 2 2 n gerçel sayısı için, x 5 m lim n eşitliği veriliyor. x 4 Buna göre, m.n çarpımı kaçtır? 1 1 1 1 2 A) B) C) D) E) 3 2 3 2 3 2 2 x 2 2 x 2 2 2 2 x 2 Çözüm: x 5 m x 5 m lim n lim n x 4 (x 2)(x 2) x 2 çarpanı sadeleşebilmelidir. Yani x 2 için pay kısmı da 0 olmalıdır. x 2 x 5 m 0 2 5 m 0 4 5 m 0 9 m 0 m 3 tür. x 5 3 lim 2 2 x 2 2 x 2 0 L’hospital uygulayabiliriz. x 4 0 2x x 5 3 lim lim x 4 2 2 x 5 2x x 2 2 2 1 lim 2 x 5 1 1 1 1 buluruz. 2 2 5 2 9 2.3 6 Buna göre; 1 1 m.n 3 buluruz. 6 2 www.matematikkolay.net 46 www.matematikkolay.net 2 x 2 ax 2 , x 2 ise f(x) x 3 x ax b , x 2 ise fonksiyonu veriliyor. lim f(x) 1 olduğuna göre, b kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 x 2 2 Çözüm: limf(x) 1 Sağdan ve soldan 1 değerini vermelidir. ax 2 x 2 için 1 ise; x 3 2a 2 2a 2 3 1 1 2a 2 1 a dir. 2 3 1 2 Aynı şekilde; x 2 için x ax b 1 ise; 4 2a b 1 3 4 2 ( ) b 1 2 4 3 b 1 b 0 buluruz. 51 2 x 3 a ve b birer gerçek sayıdır. x ax b lim 2 x 3 olduğuna göre, a b toplamı kaçtır? www.matematikkolay.net 2 x 3 2 Çözüm: x ax b lim 2 x 3 x 3 değeri paydayı 0 yapıyor. Limitin olabilmesi 0 için belirsizliği olmalıdır. Yani pay kısmı x 3 için 0 0 olmalıdır. x 3 için, x ax b 0 9 3a b 0 2 x 3 2 x 3 x 3 x 3 b 3a 9 dir. x ax 3a 9 lim 2 x 3 x 9 ax 3a lim 2 x 3 (x 3)(x 3) a(x 3) lim 2 x 3 (x 3) lim (x 3 a) x 3 x 3 2 lim(x 3 a) 2 3 3 a 2 6 a 2 a 4 9 3a b 9 3.4 b 9 12 b b 3 tür. a b 4 3 7 buluruz. 54 x 0 cosx lim limitinin değeri kaçtır? x A) Yok B) 1 C) 0 D) 1 E) www.matematikkolay.net x 0 x 0 Çözüm: cosx 1 soldan; lim x 0 cosx 1 sağdan; lim x 0 Sağdan ve soldan limitler farklı Limit yoktur. 77 2 2 x y x y 18 lim k olduğuna göre, k reel sayısının x y alabileceği değerler toplamı kaçtır? A) 12 B) 6 C) 0 D) 6 E) 12 www.matematikkolay.net 2 2 x y 2 2 2 2 2 2 Çözüm: x y 18 lim k x y 0 Bu ifadede belirsizliği oluşursa bir limit elde 0 edilebilir. Bu sebeple; x y için x y 18 0 olacaktır. y y 18 0 2y 18 y 9 2 2 2 x 3 x 3 3 2 2 2 x 3 x 3 3 y 3 tür. y 3 olursa; x 3 18 x 9 k lim lim x 3 6 dır. x 3 x 3 y 3 olursa; x 3 18 x 9 k lim lim x 3 6 dır. x 3 x 3 Toplamları 0 buluruz. 83 x 2 n bir gerçek sayı olmak üzere, |mx 12| lim n x 2 olduğuna göre, m n farkı kaçtır? A) 12 B) 6 C) 0 D) 6 E) 12 x 2 x 2 x 2 x 2 Çözüm: |mx 12| lim n kesri sadeleşebilmelidir. x 2 m 6 olursa, kesir sadeleşir. |6x 12| 6|x 2| 6 (2 x) lim lim lim x 2 x 2 1 x 2 6 dır. m n 6 ( 6) 12 buluruz. 28

