Soru Sor sayfası kullanılarak Üçgende Açılar konusu altında Muhteşem üçlü ve Açı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
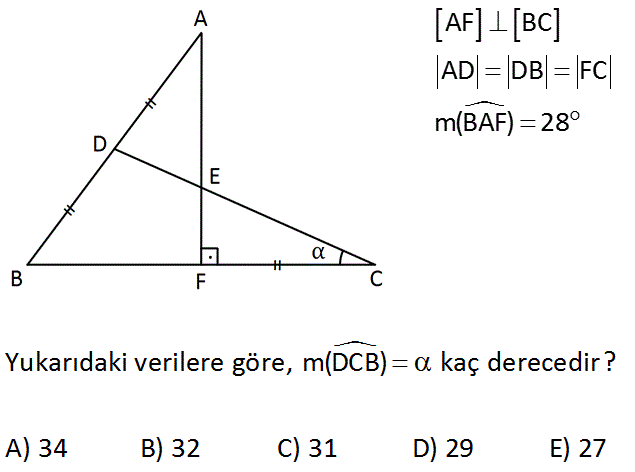

2.SORU
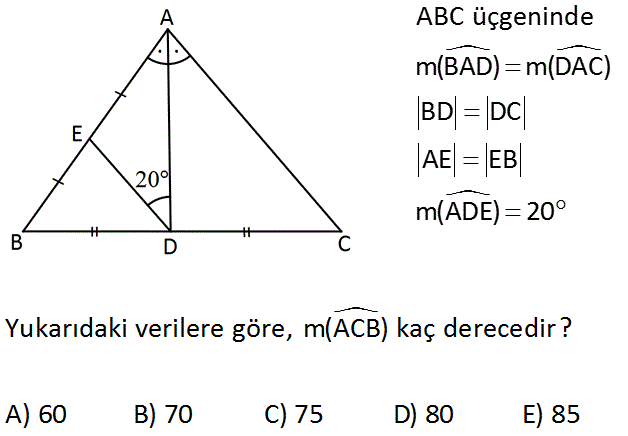
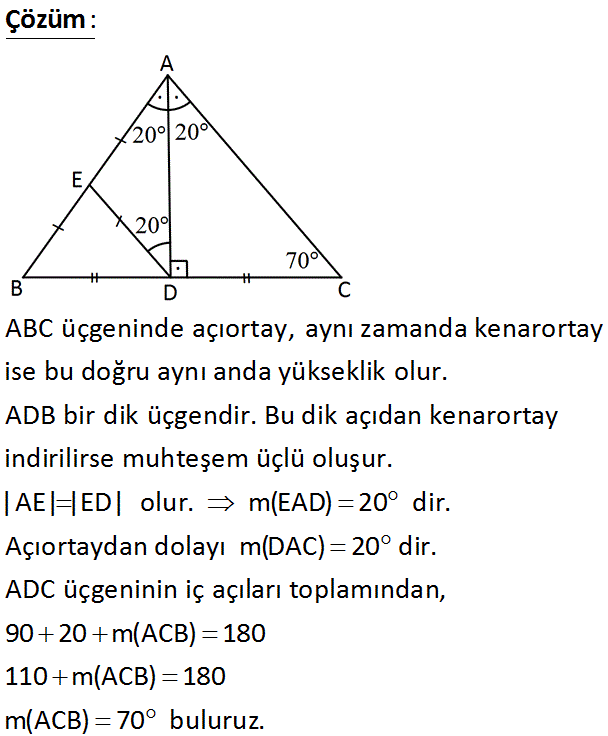
3.SORU
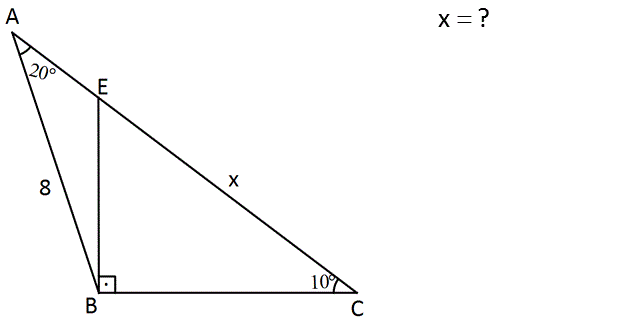
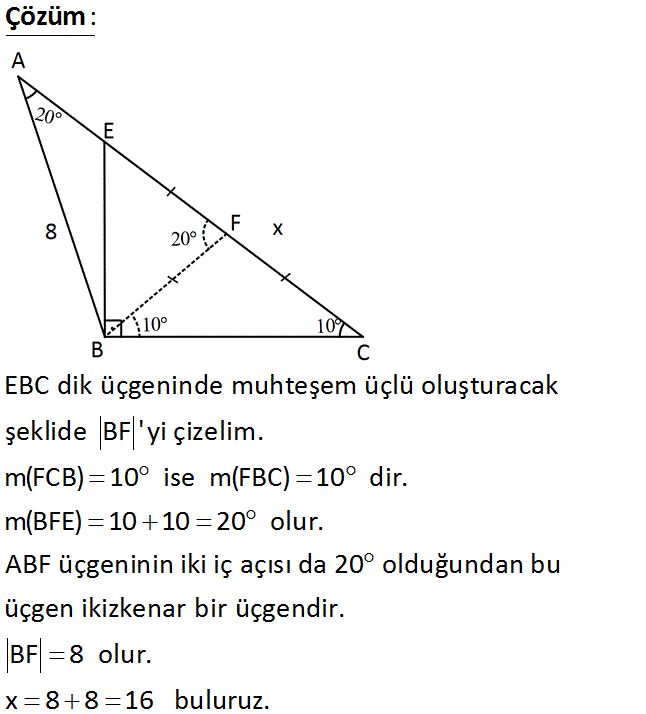
4.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
AF BC AD DB FC m(BAF) 28 www.matematikkolay.net Yukarıdaki verilere göre, m(DCB) kaç derecedir? A) 34 B) 32 C) 31 D) 29 E) 27 : Çözüm ABF dik üçgeninde DF kenarortayı çizilirse muhteşem üçlüden DF AD BD olur. ADF üçgeni ikizkenar olur. Aynı zamanda DFC üçgeni de ikizkenar olur ve açılar şekildeki gibi yerşeştirilir. DFC üçgeninde; 2 28 9 o 0 180 2 62 31 bulunur. 20
ABC üçgeninde m(BAD) m(DAC) BD DC AE EB m(ADE) 20 Yukarıdaki verilere göre, m(ACB) kaç derecedir? A) 60 B) 70 C) 75 D) 80 E) 85 www.matematikkolay.net : Çözüm ABC üçgeninde açıortay, aynı zamanda kenarortay ise bu doğru aynı anda yükseklik olur. ADB bir dik üçgendir. Bu dik açıdan kenarortay indirilirse muhteşem üçlü oluşur. |AE| |ED| olur. m(EAD) 20 dir. A çıortaydan dolayı m(DAC) 20 dir. ADC üçgeninin iç açıları toplamından, 90 20 m(ACB) 180 110 m(ACB) 180 m(ACB) 70 buluruz. 38
x? Çözüm: www.matematikkolay.net EBC dik üçgeninde muhteşem üçlü oluşturacak şeklide BF ‘ yi çizelim. m(FCB) 10 ise m(FBC) 10 dir. m(BFE) 10 10 20 olur. ABF üçgeninin iki iç açısı da 20 olduğundan bu üçgen ikizkenar bir üçgendir. BF 8 olur. x 8 8 16 buluruz. 59
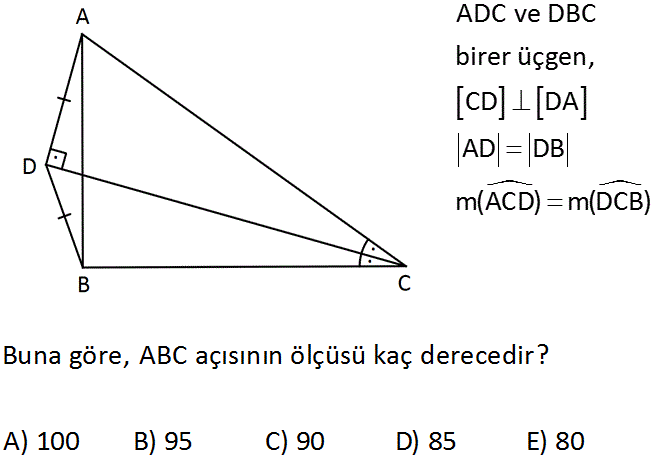
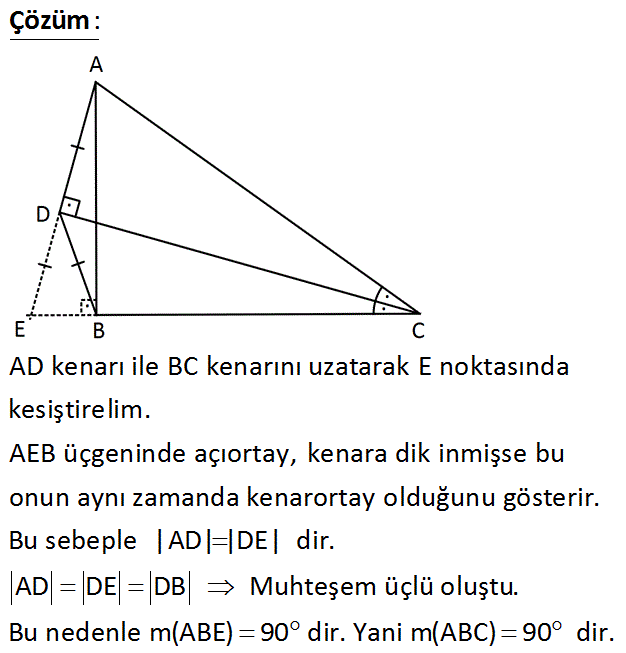
www.matematikkolay.net ADC ve DBC birer üçgen, CD DA AD DB m(ACD) m(DCB) Buna göre, ABC açısının ölçüsü kaç derecedir? A) 100 B) 95 C) 90 D) 85 E) 80 : Çözüm AD kenarı ile BC kenarını uzatarak E noktasında kesiştirelim. AEB üçgeninde açıortay, kenara dik inmişse bu onun aynı zamanda kenarortay olduğunu gösterir. Bu sebeple |AD| |DE| dir. AD DE DB Muhteşem ü çlü oluştu. Bu nedenle m(ABE) 90 dir. Yani m(ABC) 90 dir. 67


basit