 Bu bölümde Üçgende Açılar ile ilgili 19 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Üçgende Açılar ile ilgili 19 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
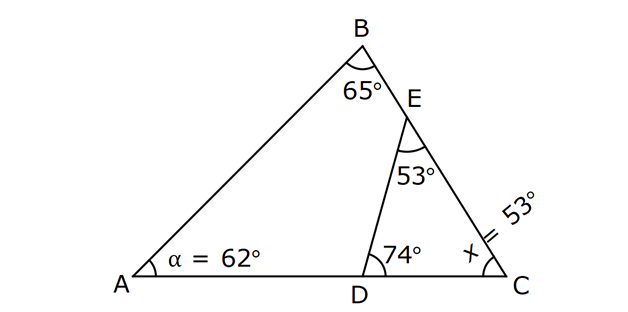
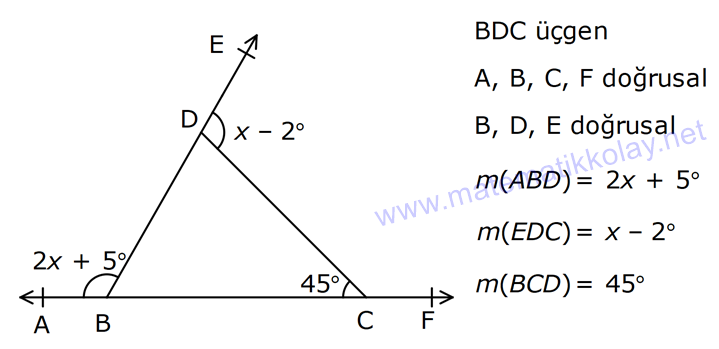
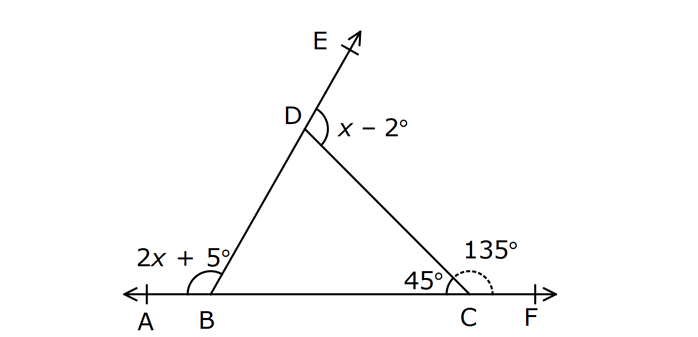
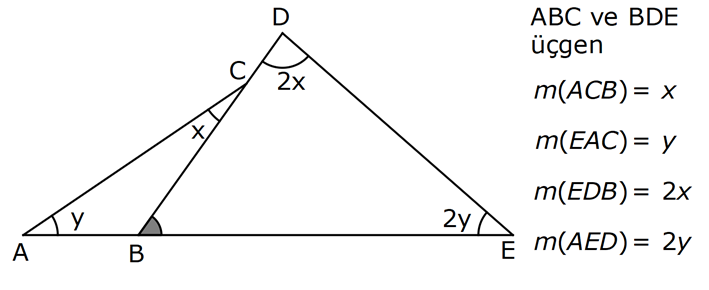
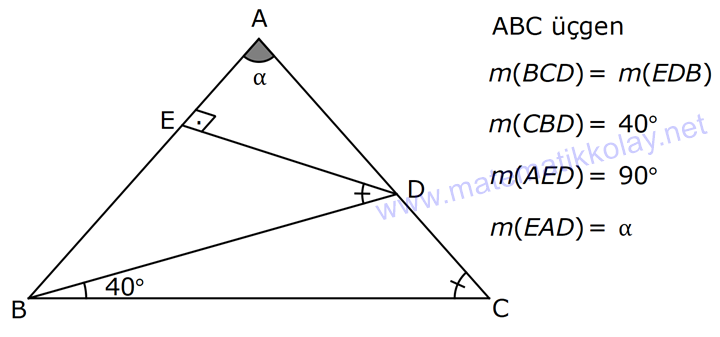
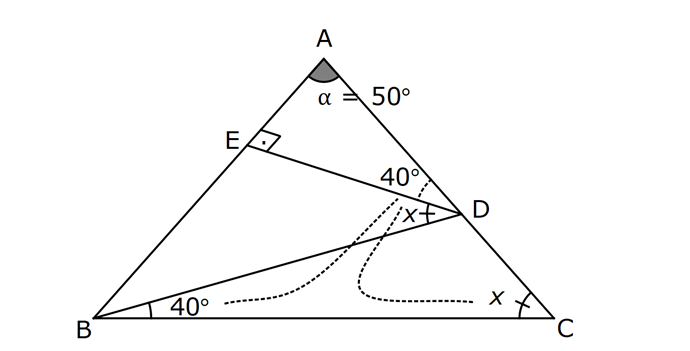
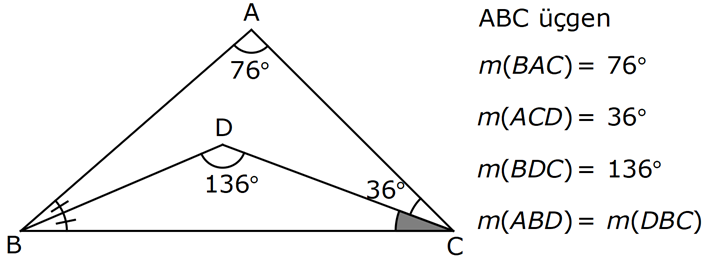
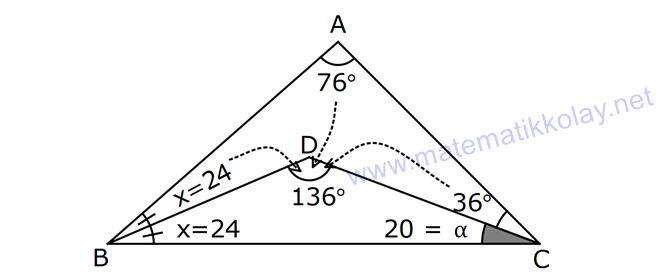
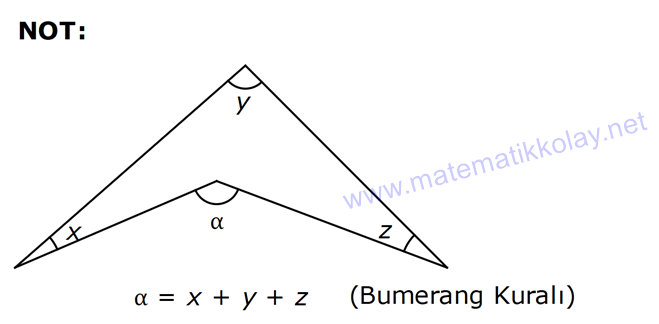
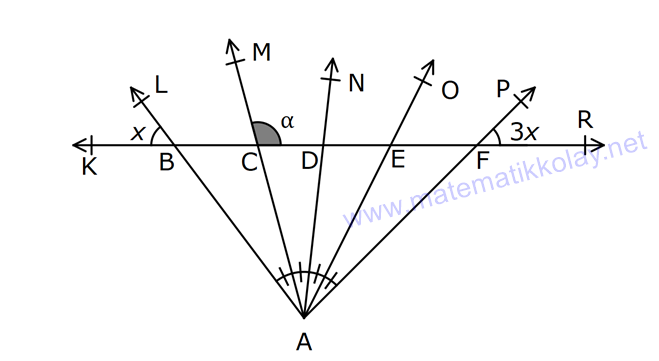
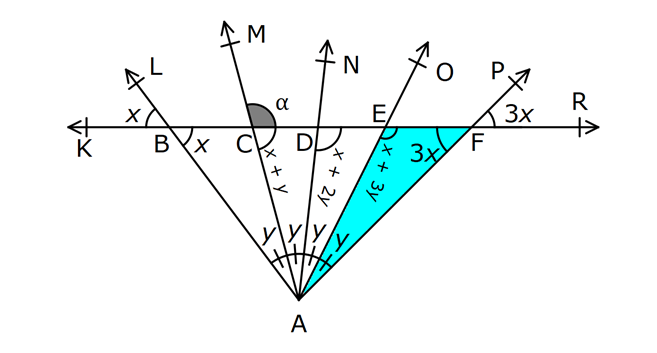
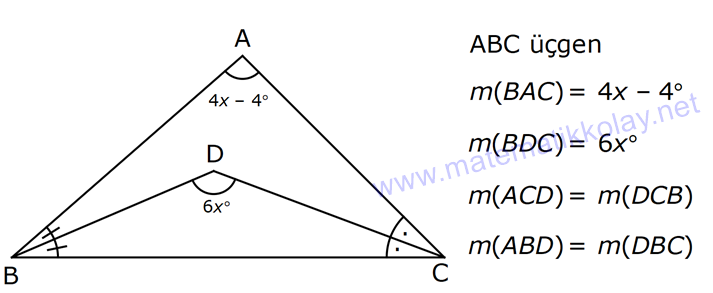
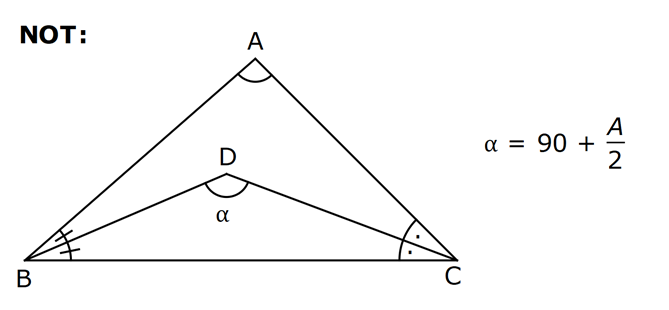
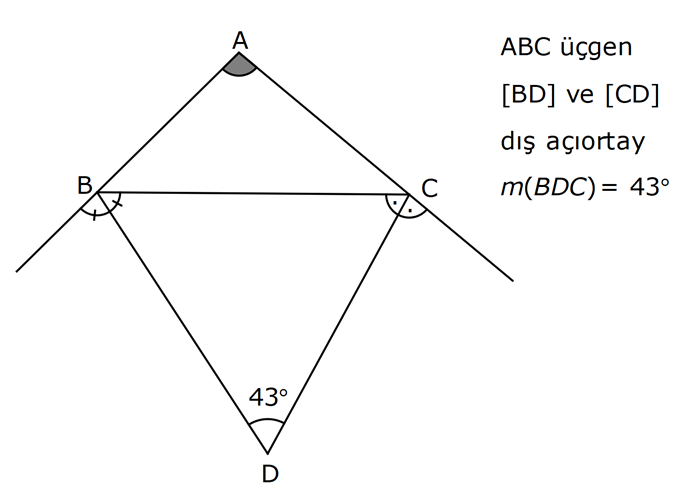
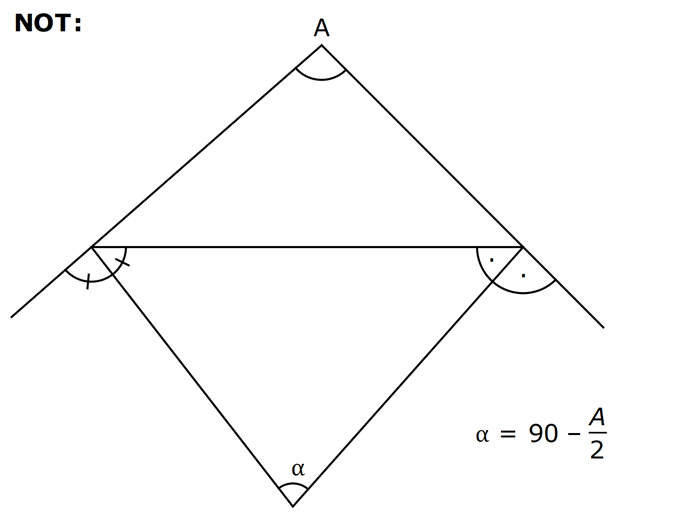
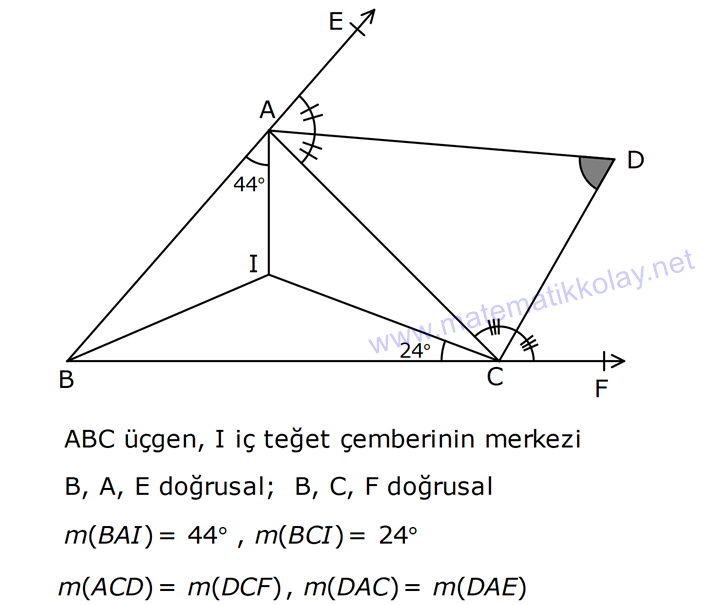
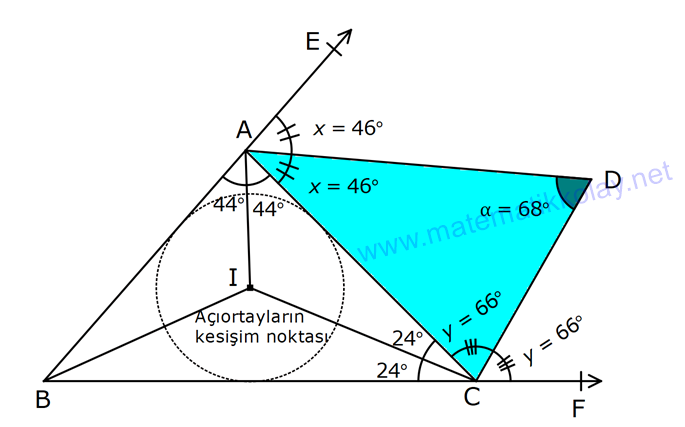
ÜÇGENDE AÇILAR www.matematikkolay.net 1) Yukarıda verilenlere göre, kaç derecedir? A) 54 B) 62 C) 65 D) 69 E) 73 ÇÖZÜM: Üçgenin iç açıları toplamı 180 dir. İlk önce EDC üçgeninden C açısını bulalım. x 53 74 180 olmalıdır. x 127 180 x 53 dir. Şimdi ABC üçgeninin iç açıları toplamından yı bulabiliriz. 65 53 180 1 Not: 18 180 62 dir. Cevap: B 2) Yukarıda verilenlere göre, x kaç derecedir? A) 74 B) 67 C) 63 D) 59 E) 55 ÇÖZÜM: Üçgenin dış açıları toplamı 360 dir. 45 nin olduğu yerde üçgenin dış açısı 180 45 135 dir. Dış açıların toplamı 360 olması gerektiğinden 2x 5 x 2 135 360 3x 3 135 360 3x 138 360 3x 222 x 7 Not: 4 dir. Cevap: A 3) İç açılarının ölçüleri 3, 4, 6 ile ters orantılı olan üçgenin en büyük dış açısı kaç derecedir? A) 110 B) 120 C) 130 D) 140 E) 150 www.matematikkolay.net ÇÖZÜM: İç açılarına x, y ve z diyelim. 3x 4y 6z eşitliğini kurabiliriz. EKOK(3, 4, 6) 12 olduğundan 3x 4y 6z 12k diyelim. x 4k, y 3k, z 2k olur. 4k 3k 2k 180 9k 180 k 20 dir. En büyük dış açı, en küçük iç açını n yanındadır. En küçük iç açı 2k 2.20 40 dir. En büyük dış açı 180 40 140 dir. Cevap : D 4) Yukarıdaki verilenlere göre, m(EBD) kaç derecedir? A) 30 B) 40 C) 45 D) 50 E) 60 ÇÖZÜM: Bir üçgende dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir. m(EBD) x y dir. BDE üçgeninin iç açıları toplamından x y 2x 2y 180 3x 3y 180 x y 60 dir. m(EBD) 60 dir. Cevap : E Not: 5) Yukarıdaki verilenlere göre, kaç derecedir? A) 30 B) 40 C) 45 D) 50 E) 60 ÇÖZÜM: m(BCD) m(EDB) x olsun. m(BCD) x ile m(CDB) 40 nin toplamı m(BDA)’yı verir. Burda x açısı zaten var olduğundan m(EDA) 40 olur. AED üçgeninin iç açıları toplamından, 90 40 180 50 buluruz. Cevap : D 6) Yukarıdaki verilenlere göre, m(BCD) kaç derecedir? A) 10 B) 16 C) 20 D) 24 E) 30 ÇÖZÜM: www.matematikkolay.net m(ABD) m(CBD) x diyelim. Bumerang kuralına göre, 76 x 36 136 olmalıdır. x 112 136 x 24 dir. BDC üçgeninin iç açıları toplamından, 24 136 180 dir. 160 180 20 dir. Cevap: C 7) m(KBL) x , m(PFR) 3x , m(MCR) m(LAM) m(MAN) m(NAO) m(OAF) olduğuna göre, kaç derecedir? A) 105 B) 110 C) 120 D) 130 E) 135 ÇÖZÜM: m(ABC) x tir. Eşit açılar y olsun. m(ACD) x y olur (BCA üçgeninde dış açı). m(ADE) x 2y olur (ACD üçgeninde dış açı). m(ADE) x 3y olur (ADE üçgeninde dış açı). m(AFE) 3x tir. AFE üçgeninde iç açıların top 45 lamından x 3y y 3x 180 4x 4y 180 x y 45 dir. x y 180 olması gerektiğinden (Doğru Açı) 135 dir. Cevap : E 8) Yukarıdaki verilenlere göre, x kaç derecedir? A) 14 B) 18 C) 22 D) 26 E) 30 ÇÖZÜM: Açıortayların, içerde kesiştiği noktada açıyı bulmak A için 90 formülünü kullanabiliriz. 2 4x 4 6x 90 2 6x 90 2x 2 4x 88 x 22 dir. Cevap : C www.matematikkolay.net 9) Yukarıdaki verilenlere göre, m(BAC) kaç derecedir? A) 82 B) 86 C) 92 D) 94 E) 96 ÇÖZÜM: Dış açıortayların kesiştiği noktada açıyı bulmak A için 90 formülünü kullanabiliriz. 2 A 43 90 2 A A 90 43 47 A 94 dir. 2 2 Cevap: D 10) Yukarıdaki verilenlere göre, m(ADC) kaç derecedir? A) 68 B) 72 C) 74 D) 76 E) 78 ÇÖZÜM: www.matematikkolay.net Üçgenin iç açıortayları bir noktada kesişir ve bu nokta iç teğet çemberinin merkezidir. Bu nedenle I noktaktasına giden doğrular birer açıortaydır. m(ICA) 24 ve m(IAC) 44 olur. Şimdi dış açıortay Not: ların ayırdığı açıları bulalım. 44 44 x x 180 88 2x 180 2x 92 x 46 dir. 24 24 y y 180 48 2y 180 2y 13 2 y 66 dir. ADC üçgeninin iç açıları toplamından 46 66 180 112 180 68 dir. Cevap : A
 Bu bölümde Üçgende Açılar ile ilgili 19 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Üçgende Açılar ile ilgili 19 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar… 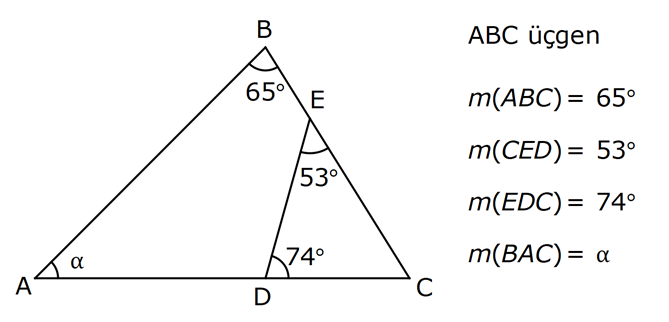
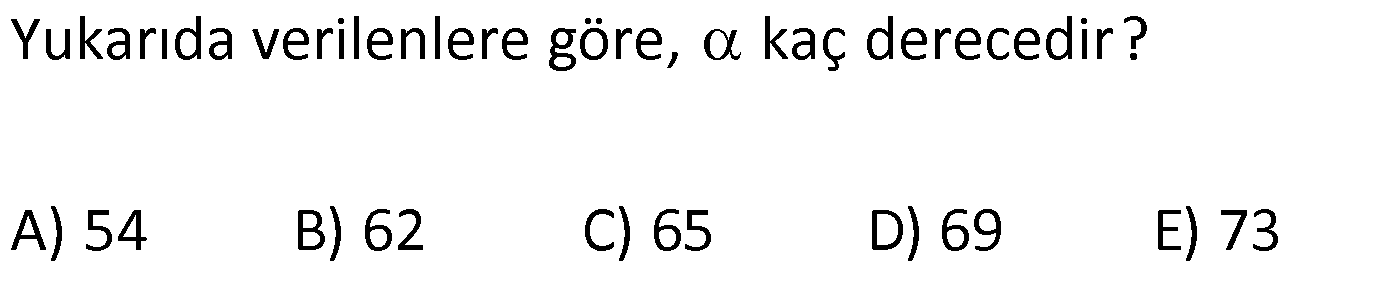

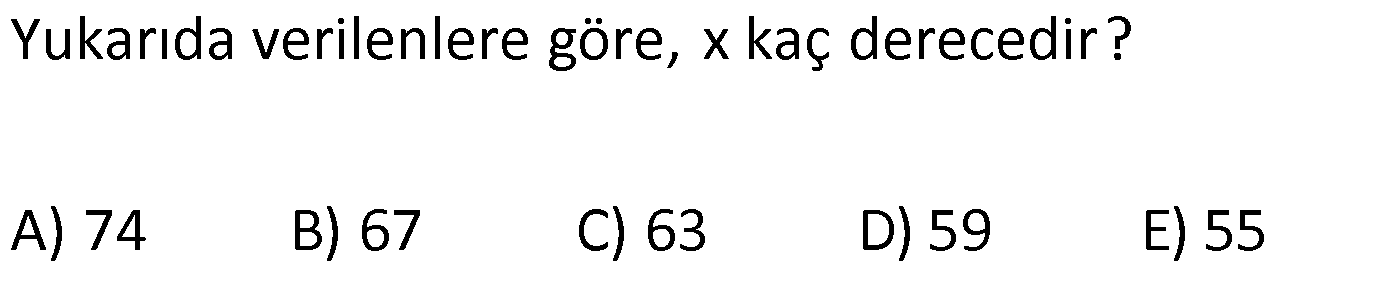




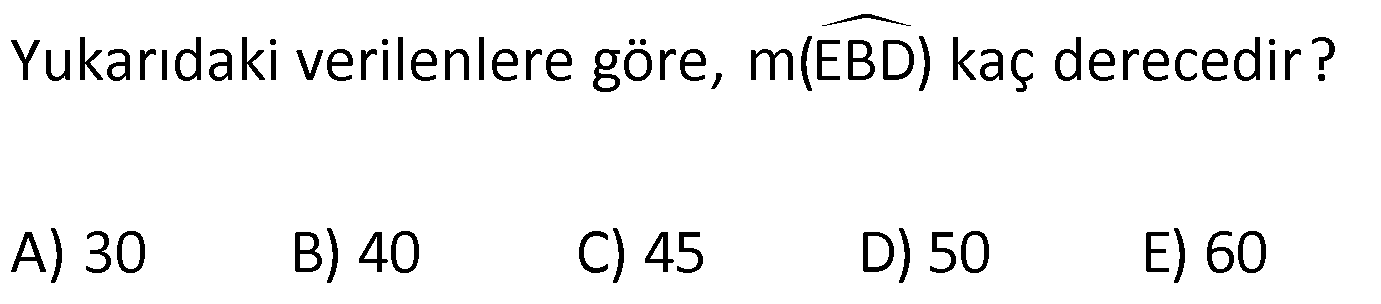

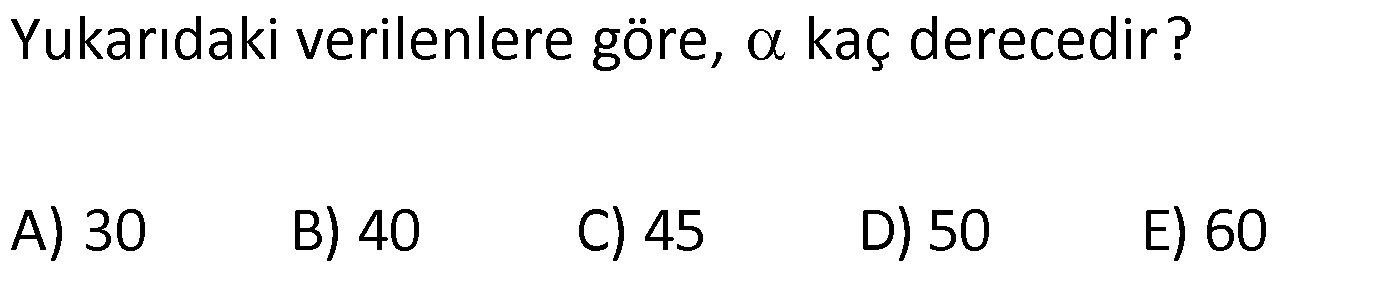

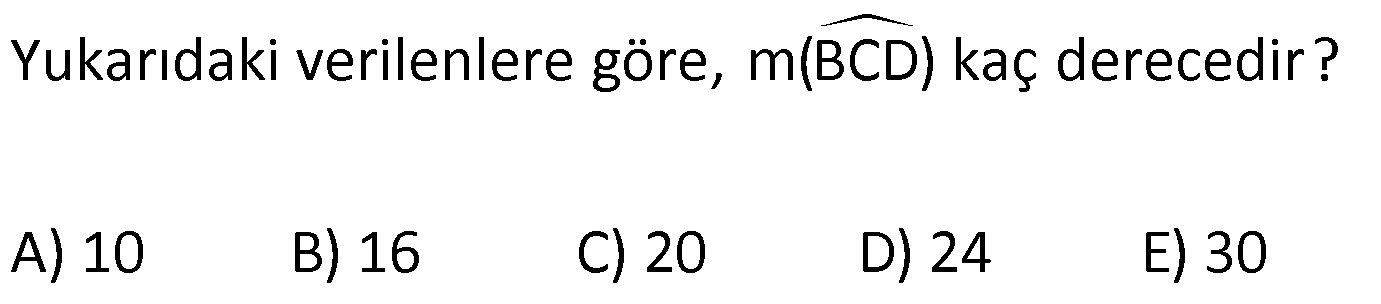

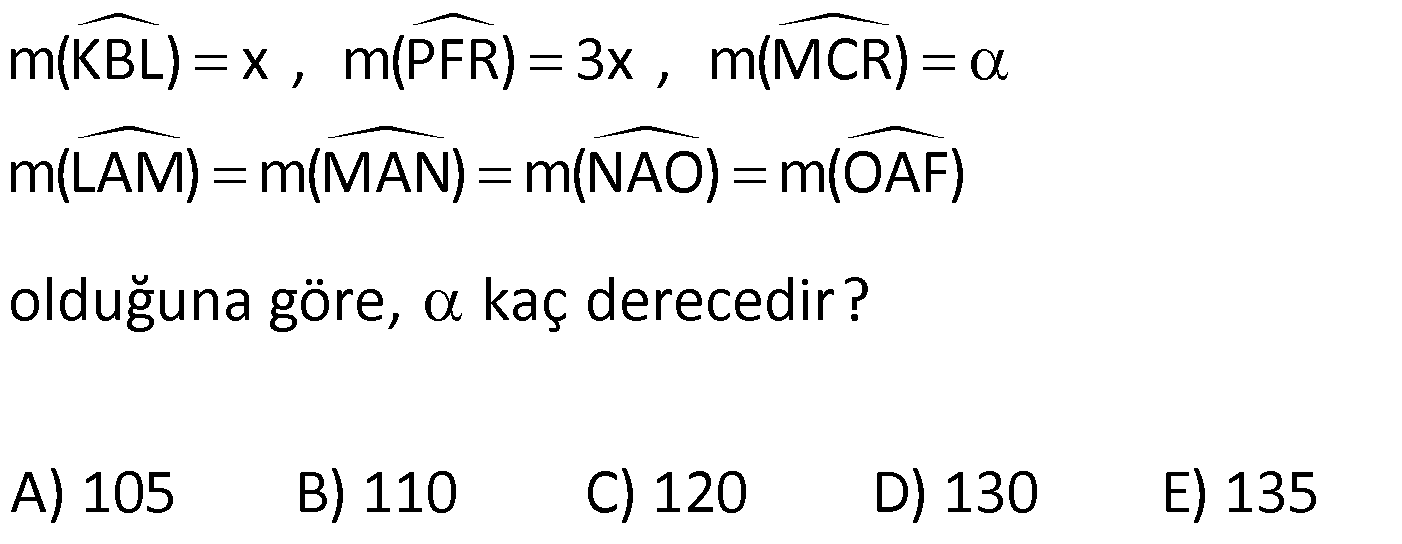

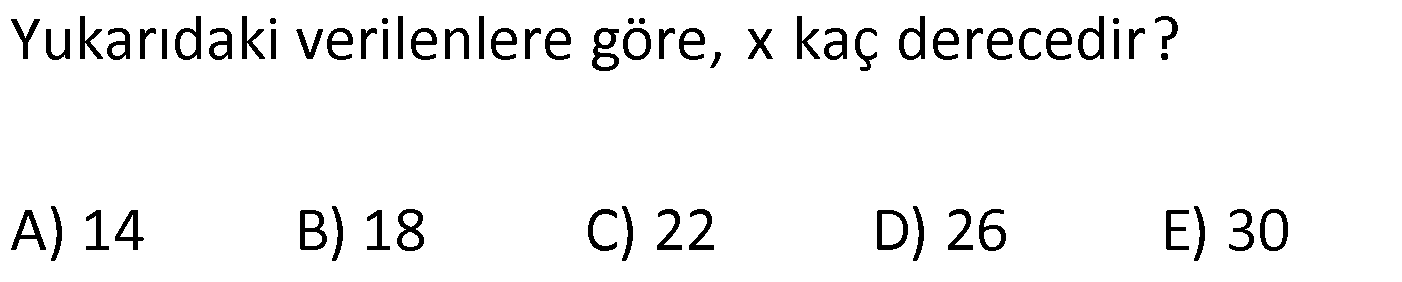


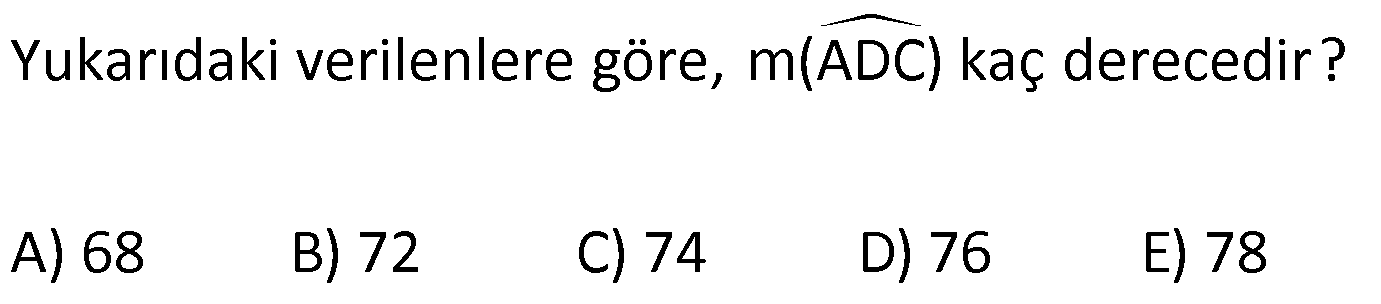




gayet güzel
meraba, bu 90-2x-30bölü2
neden x+15 oldu x-15 olmasıgerekmez mi
– işareti içeriye dağıtıldığı için x+15 olur.
Neresi güzel ya
Vallaha Haklısn
Çok güzel sorular çok beğendim 👍
asena güzel değşlse yapama bence gayet güzel
Offffff çok zordu beynim dondu
Hayır ya hiç güzel değil bu ne
Tşkkklr sağoln işimi gördü proje odevimdi yptm
teşekkür ederim bence yeterince güzel elinize emeğinize sağlık projeme yardımcı oldunuz
sorular aşırı basit
Çok güzel
bence gayet güzel açıklanmış sorular ve yeni öğrenmeye başlayanlar için çok iyi
Eyw teşekkür ederim çok iyi sorularınız vardı 🙂
Bunkar 9. Sinif doğrumu
9.sınıf evet.
Aynı zamanda TYT ye hazırlık.
bana biraz basit geldi. ama güzel sorular ve kısa çözümler içeren sorular da var