Soru Sor sayfası kullanılarak Türev konusu altında Türevin varlığı, Türev için gerekli şartlar, Türev Süreklilik İlişkisi, Türevsiz olduğu noktalar ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
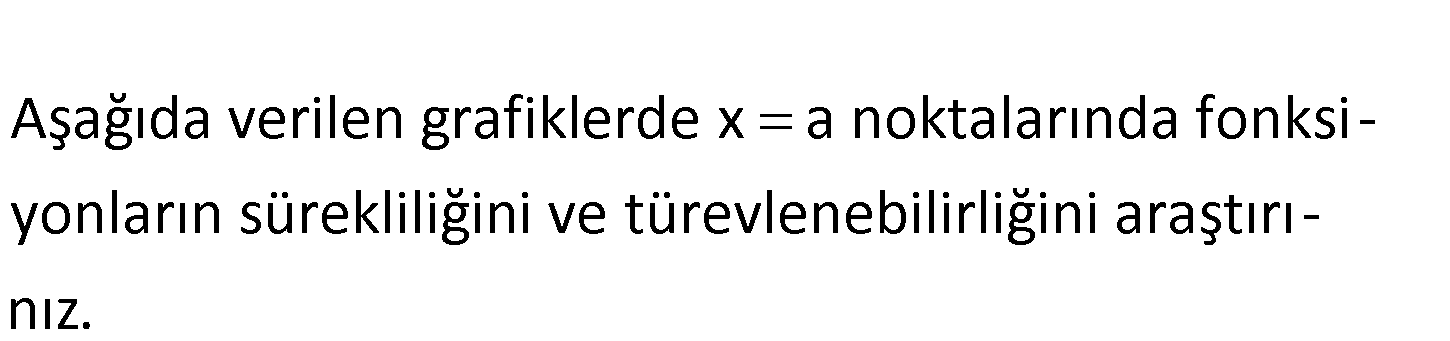

2.SORU

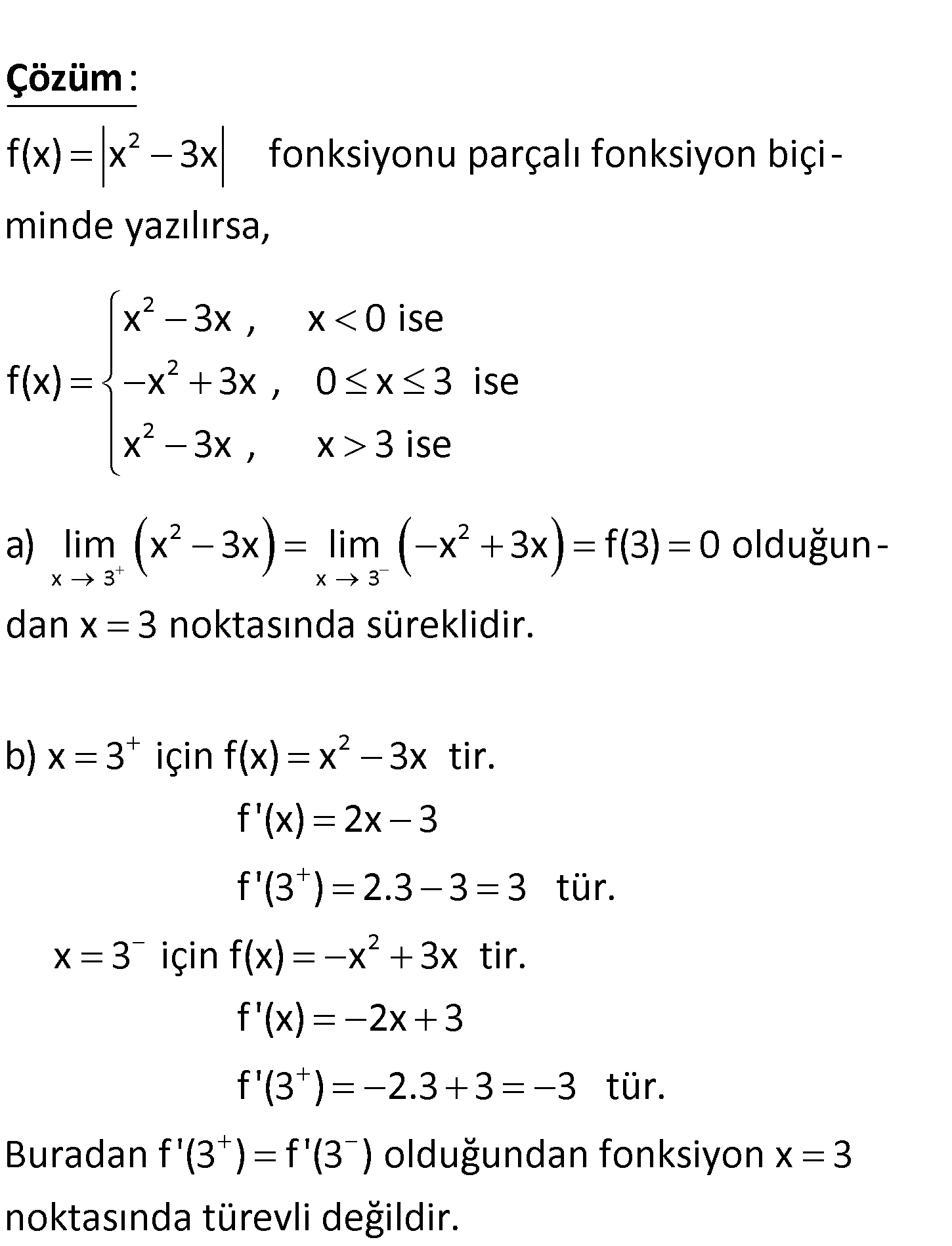
3.SORU
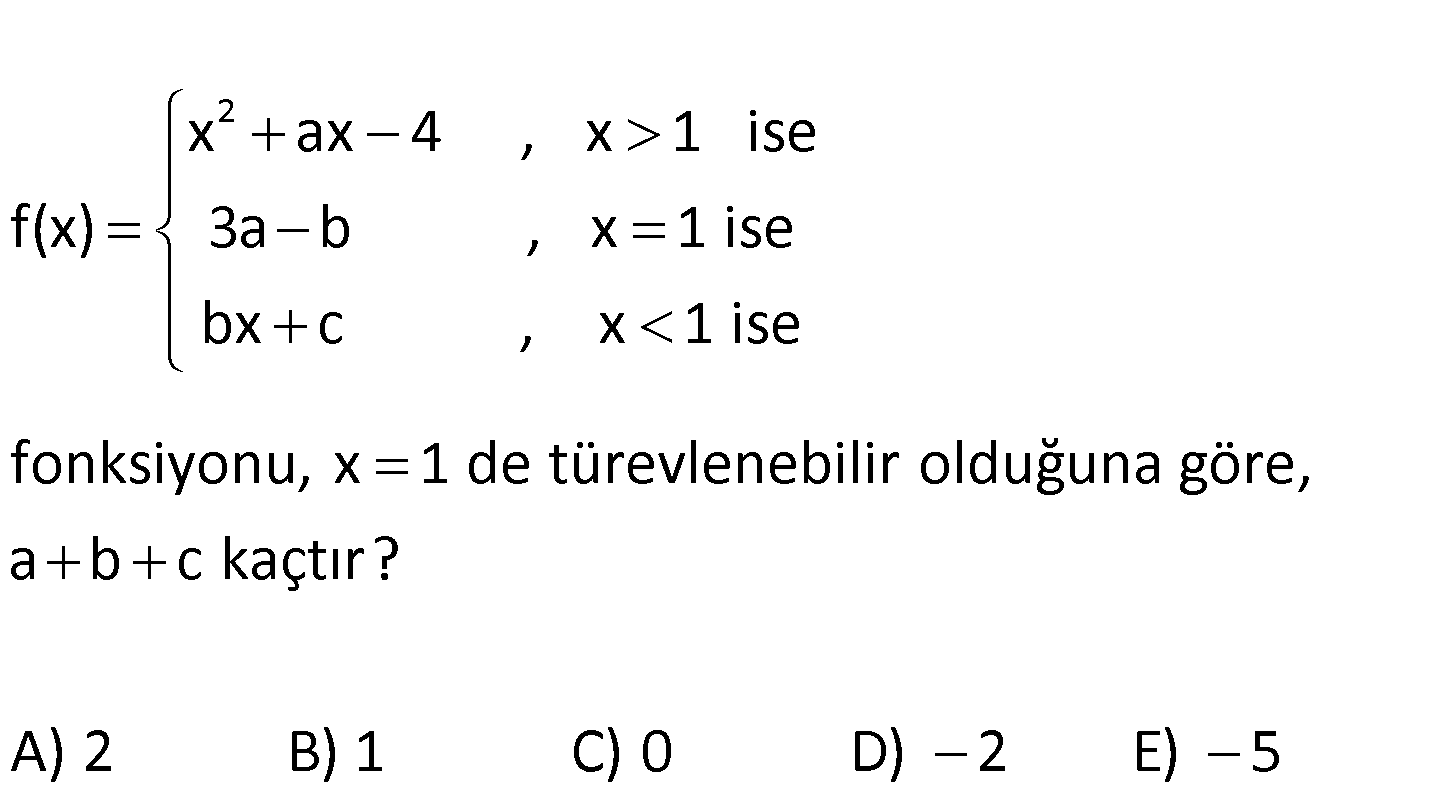

4.SORU
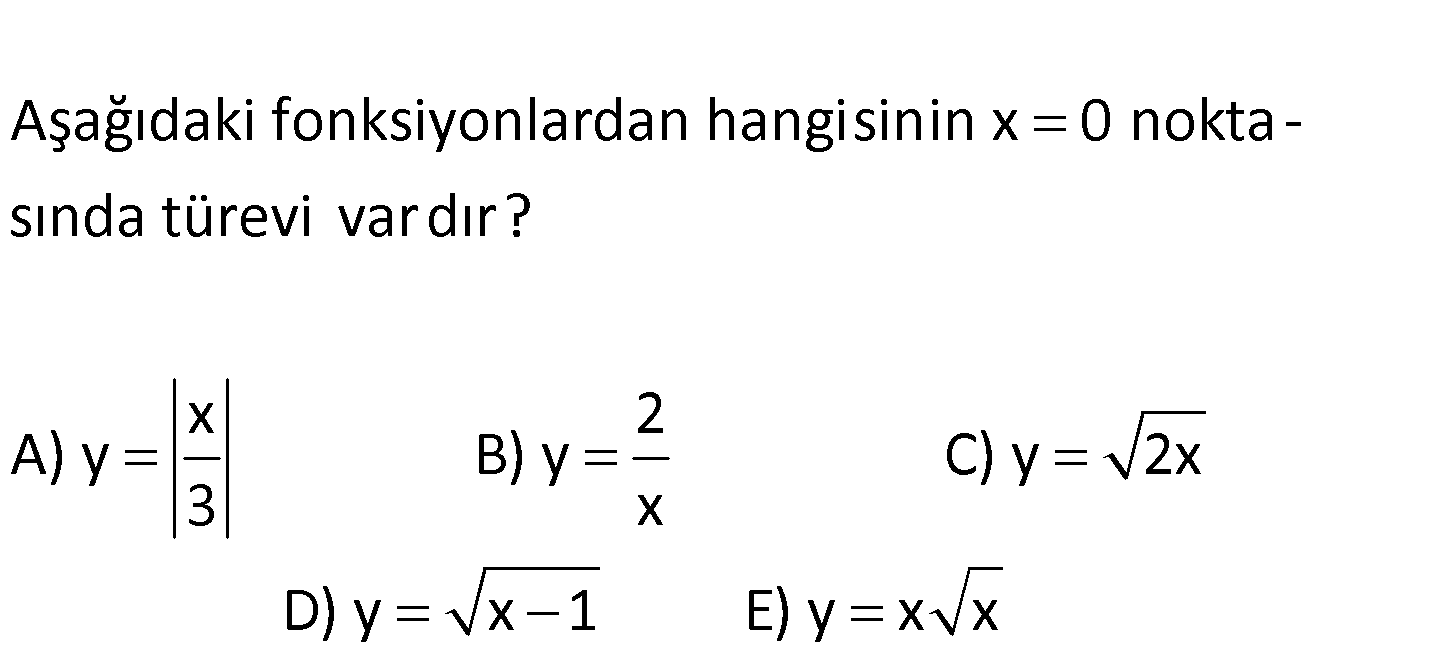

5.SORU


6.SORU


7.SORU


8.SORU


9.SORU


10.SORU
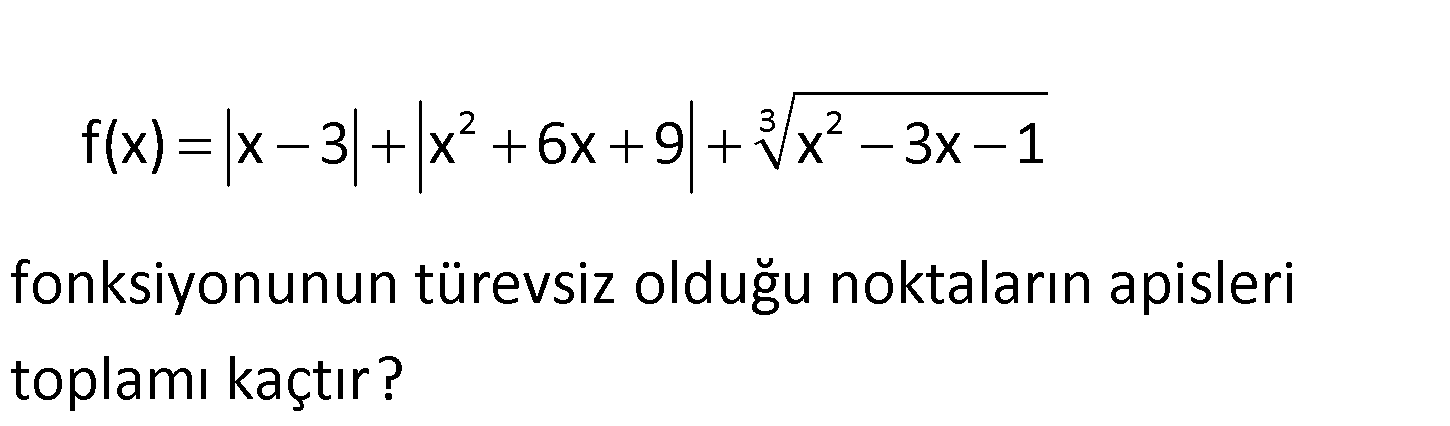

11.SORU


12.SORU


13.SORU


14.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Türevin varlığı, Türev için gerekli şartlar, Türev Süreklilik İlişkisi, Türevsiz olduğu noktalar
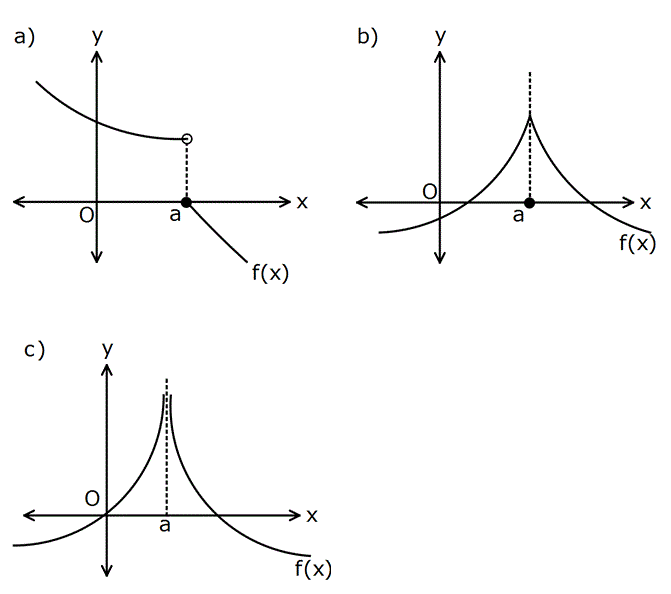
Aşağıda verilen grafiklerde x a noktalarında fonksi – yonların sürekliliğini ve türevlenebilirliğini araştırı – nız. www.matematikkolay.net a) f(x) fonksiyonu x a noktasında sürekli değildir. Fonksiyonun bu noktada türevi : yoktu Çözüm r. b) f(x) fonksiyonu x a noktasında süreklidir. Ancak bu noktada fonksiyon kırılmaktadır. x a noktasından fonksiyona birden fazla teğet çizebileceğinden fonksiyonunun bu noktada türevi yoktur. c) f(x) fonksiyonu x=a noktasında tanımlı değildir. Dolayısı ile fonksiyon x=a noktasında sürekli değildir. Fonksiyonun bu noktada türevi yoktur. www.matematikkolay.net 175
2 f(x) x 3x fonksiyonu veriliyor. a) f fonksiyonu x 3 noktasında sürekli midir? b) f fonksiyonu x 3 noktasında türevli midir? 2 2 2 f(x) x 3x fonksiyonu parçalı fonksiyon biçi – minde yazılırsa, x 3x , x 0 ise f(x x : ) Çözüm 2 2 2 x 3 x 3 2 3x , 0 x 3 ise x 3x , x 3 ise a) lim x 3x lim x 3x f(3) 0 olduğun – dan x 3 noktasında süreklidir. b) x 3 için f(x) x 3x tir. f ‘(x) 2x 3 2 f ‘(3 ) 2.3 3 3 tür. x 3 için f(x) x 3x tir. f ‘(x) 2x 3 f ‘(3 ) 2.3 3 3 tür. Buradan f ‘(3 ) f ‘(3 ) olduğundan fonksiyon x 3 noktas ında türevli değildir. 176
2 x ax 4 , x 1 ise f(x) 3a b , x 1 ise bx c , x 1 ise fonks iyo nu, x 1 de türevlenebilir olduğuna göre, a b c kaçtır? A) 2 B) 1 C) 0 D) 2 E) 5 www.matematikkolay.net Türevin olabilmesi için ilk şart sürekliliktir. Yani x 1’e sağdan veya soldan yaklaşıldığınd : a Çözüm x 1 x 1 ki değeri ile x 1’deki değeri aynı olmalıdır. lim f(x) f 1 lim f(x) 1 a 4 3a b b c a 3 3a b b c I.eşitlik Ayrıca, sağdan ve soldan türevler birbirine eşit olmalıdır. x 1 için f ‘(x) 2x a 2:00 AM f ‘(1 ) 2 a dır. x 1 için f ‘(x) b f ‘(1 ) b dir. O halde; 2 a b dir. I.eşitliğe göre; a 3 3a b idi. a 3 2a 2 1 1 1 1 a dır. b 2 a 2 1 1 dir. I.eşitlikten; 3 a b b c 3 1 1 c c 5 dir. Buna göre; a b c 1 1 5 5 buluruz. 117
www.matematikkolay.net Aşağıdaki fonksiyonlardan hangisinin x 0 noktasında türevi var dır? x 2 A) y B) y C) y 2x 3 x D) y x 1 E) y x x x A) x=0 noktasına sağdan yaklaşıldığında 3 x 1 ‘ün türevi ; soldan 3 3 : Çözüm yaklaşıldığında ise x 1 ve türevi olur. Türev yoktur. 3 3 2 B) y= x=0 için tanımsızdır. Türev yoktur. x 1 C) 2x in türevi x=0 için tanımsız, 2x Türev yoktur. D) y= x 1 x=0 için tanımlı değildir. Türev yoktur. E) y=x x in türevi 1 x 1. x x = x 2 x 2 3 x Türevi olmasını 2 engelleyen bir durum yok. 5
2 a ve b birer gerçek sayı olmak üzere, x 2x , x 1 f(x) ax b , x 1 fonksiyonu x 1 için tür evli olduğuna göre, a.b çarpımı kaçtır? A) 4 B) 2 C) 1 D) 0 E) 2 www.matematikkolay.net Sağdan ve soldan türevi aynı olmalıdır. Sağdan f ‘(1) 2x 2 2.1 2 4 tür. Soldan f ‘(1) : a a 4 Çözüm 2 tür. x 1 noktasında fonksiyon sürekli olmalıdır. x 1 için aynı değeri vermelidir. Sağdan f(1) x 2x 1 2 3 tür. Soldan f(1) 4x b 4.1 b 3 b 1 dir. a.b 4.( 1) 4 buluruz. 45
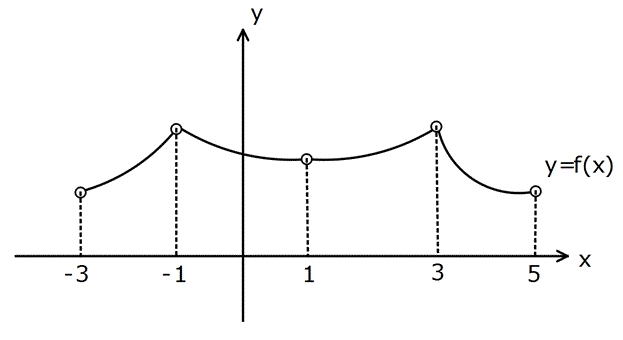
Yukarıda grafiği verilen f(x) fonksiyonu aşağıda veri – len aralıklardan hangisinde her noktada türevlidir? A) (-3, 1) B) (1, 5) C) (-3, 5) D) (-1, 3) E) (-1, 1) www.matematikkolay.net Türevin olabilmesi için, fonksiyon sürekli olmalıdır. Grafikte boşluk,atlama zıplama olm : amalı Çözüm dır. Sadece E şıkkındaki aralıkta süreklilik sağlanıyor. Diğer şıklarda ise boşluk olan noktalar var. Bu sebeple cevap:E dir. 49
2 2 3x 2ax , x 1 f(x) 2ax bx , x 1 fonksiyonu her x gerçek sayısı için türevlenebilir olduğuna göre, a.b çarpımı kaçtır? www.matematikkolay.net 2 2 x 1 için iki fonksiyon da aynı değeri vermelidir. (Süreklilik) x 1 3x 2ax 2ax bx : Çözüm 3 2a 2a b 3 b 4a dır. x 1 için türevleri eşit olmalıdır. x 1 6x 2a 2a 2bx 6 2a 2a 2b 6 2b 4a ( 3 b 4 a) 6 2b 3 b 3 b a 0 dır. a.b 0.3 0 buluruz. 52
2 3 2x 3a , x 1 f(x) x bx , x 1 fonksiyonu tüm x gerçek sayıları için türevli olduğu – na gör e, a.b çarpımı kaçtır? A) 1 B) 0 C) 1 D) 2 E) 3 www.matematikkolay.net 2 f ‘(1 ) f ‘(1 ) olmalıdır. 4x 3x b 4 3 b b 1 dir. f(1 ) f(1 ) olmalıdır. S : ( Çözüm 2 3 üreklilik) 2x 3a x bx 2 3a 1 b 1 3a b 1 3a 1 a 0 dır. a.b 0.1 0 buluruz. 58
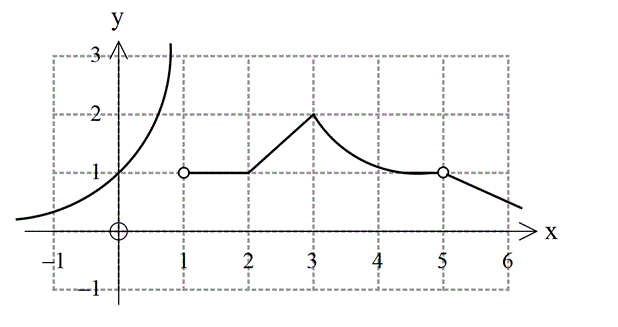
Yukarıda f(x) fonksiyonunun bir parçasının grafiği verilmiştir. f(x) fonksiyonu kaç noktada sürekli olduğu hâlde türevlenemez? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net Grafikteki kesintisiz sivri uçlarda fonksiyon süreklidir. Fakat türevlenemez.Buna göre; 2 : ve 3 Çözüm noktalarında fonksiyon süreklidir ama türevli değildir. 2 nokta bulunur. 59
2 3 2 f(x) x 3 x 6x 9 x 3x 1 fonksiyonunun türevsiz olduğu noktaların apisleri toplamı kaçtır? www.matematikkolay.net 2 3 2 f(x) x 3 x 6x 9 x 3x 1 x 3 ifadesi için 3 değerine sağdan ve soldan yaklaşıldığında içeris : Çözüm 2 2 i pozitif veya negatif oluyor, sağdan ve soldan türevleri eşit olmuyor.Bu yüzden fonksiyon x 3 noktasında türevlenemez. x 6x 9 (x 3) ifadesi sürekli pozitif olduğundan fonksiyonun değişim gösterdiği 3 2 ı 3 2 2 2 bir nokta yoktur. Her noktada türevlenebilir. x 3x 1 ifadesinin türevini aldığımızda; 2x 3 x 3x 1 ifadesinin paydayı 3 (x 3x 1) 0 yapan değerlerinde tanımsızlık olacağı için bu noktalarda türevlene 2 mez. x 3x 1 0 denkleminin kökler toplamı; b 3 3 tür. a 1 Türevsiz olunan noktaların apsislerinin toplamı; 3 3 6 bulunur. 74
2 f : R R parçalı fonksiyonu 3x 2 , x tam sayıysa f(x) x , x tam sayı değilse biçiminde tanı mlanıyor. Buna göre, I. f fonksiyonu x 0 noktasında süreklidir. II. f ‘(1) 3 tür. III. x (0, 1) ise f ‘(x) (0, 2) dir. ifadelerinden hangileri doğrudur? A) Yalnız I B) Yalnız III C) I ve II D) II ve III E) I, II ve III www.matematikkolay.net x 0 x 0 x 0 Süreklilik için lim f(x) lim f(x) f(0) sağlanmalıdır. f(0) 3x 2 2 dir. lim f(x) : li Çözüm 2 x 0 m f(x) x 0 dır. Üçü birbirine eşit ol – madığından süreklilik yoktur. Tam sayı olan x değerleri için sürekliliğin olmadığı – nı görüyoruz. Bu sebeple tam sayı değerlerde türev yoktur. f ‘(1) 3 yanlışt 2 ır. x, 0 ile 1 arasında ise f(x) x f ‘(x) 2x 0 ile 2 arasındadır. Cevap: B 90
4 0 x 0 f(x) x x 0 fonksiyonu için x 0 da I. f ‘(x) tanımlıdır. II. f ”(x) tanıml -4 ıdır. III. f ”'(x) tanımlıdır. IV. f (x) tanımlıdır. ifadelerinden hangileri doğrudur? A) I ve II B) I, II ve III C) I ve IV D) Yalnız I E) Yalnız IV www.matematikkolay.net Türevin olabilmesi için, fonksiyon sürekli olmalı. Ayrıca sağdan ve soldan türev eşit ol : malıd Çözüm 3 2 ır. I. x 0 için f ‘(x) 4x x 0 için f ‘(x) 0 x 0 için f ‘(x) 0 x 0 için f ‘(x) 0 Türev tanımlıdır. II. x 0 için f ”(x) 12x x 0 için f ”(x) 0 x 0 için f ”(x) 0 x 0 4 4 için f ”(x) 0 Türev tanımlıdır. III. x 0 için f ”'(x) 24x x 0 için f ”'(x) 0 x 0 için f ”'(x) 0 x 0 için f ”'(x) 0 Türev tanımlıdır. IV. x 0 için f (x) 24 x 0 için f (x) 4 4 24 x 0 için f (x) 0 x 0 için f (x) 0 Türev tanımlı değildir. Cevap: B 107
2 2 fonksiyonunun türevsiz olduğu noktaların apsisleri – nin t x x opl 12 f(x) x 1 amı kaçtır? A) 12 B ) 1 C) 0 D) 1 E) 12 www.matematikkolay.net 2 2 x x 12 ifadesinde süreklilik nasıl, bakalım. x 1 Payda daima pozitif, sürekliliği : bozacak Çözüm bir yapıya sahip değil. Pay kısmı ya 0, ya da pozitif. Burdan da bozulmaz. Süreklilik açısından bir sorun yok. Payı 0 yapan noktalardaki sağdan ve soldan türevlere bakalım. Muhtemelen burada farklı de 2 2 2 2 2 2 2 ğerler oluşacak ve türevsizlik meydana gelecek. x x 12 x 4 x 3 x 4 x 3 x 1 x 1 x 1 4 x . x 3 x 3 için f x x 1 4 x x 3 dir. x 1 4 x . x 3 3 x 4 için f x x 1 2 2 4 x x 3 dir. x 1 4 x . x 3 4 x için f x tür. x 1 Bu yüzden x 3 ün solunda türev a’ya eşit ise sağında a ya eşit olacak. x 4 ün solunda türev b ye eşit ise, sağında b ye eşit olacak. Sağdan ve soldan türev birbirine eşit değilse, orda türev yoktur. Apsisler toplamı 4 3 1 buluruz. www.matematikkolay.net 130
2 2 3 2 2 fonksiyonunun türevsiz olduğu x değ x 3 f(x) x 4x 2 x 5x 2 x erlerinin top – la 3x mı kaçtır? 1 1 A) 2 B) 3 C) 5 D) 6 E) 8 2 2 3 2 2 x 3 x 4x 2 x 5x 2 x 3x 11 Mutlak değerin içini 0 yapan değerlerde türev yoktur. Solda : n ve Çözüm 2 2 2 2 sağdan türev farklı olur. x 4x 2 0 b 4 Kökler toplamı 4 tür. a 1 x 3 paydayı 0 yapan x değerleri x 3x 11 bu kesri tanımsız yapar. Dolayısıyla türevi olmaz. 3 x 3x 11 0 Kökler toplamı 3 tü 1 3 2 3 2 2 r. 2x 5 x 5x 2 in türevi dir. 3 x 5x 2 Paydayı 0 yapan x değerinde tanımsız olacaktır. 5 x 5x 2 0 Kökler toplamı 5 tir. 1 Tüm kökleri toplarsak; 4 3 5 6 buluruz. www.matematikkolay.net 131


Emekleriniz için çok teşekkür ederiz biz öğrenciler için rica etsek buradaki çözümlü soruları PDF haline getirebilir misiniz?.Telefondan veya laptoptan bakarak çözmek pek verimli olmuyor ayt soruları PDF li olsa gerçekten çok iyi olur olur veya olmaz cevabınız için şimdiden teşekkür ediyorum bu kadar soruyu görmek dahi bir nimet sonuçta…
Maalesef, zamanında burdaki sorular için pdf hazırlamadık.
Gelen talepler neticesinde, yeni hazırladığımız her yerde pdf koyuyoruz.
Zamanla buraları tekrar düzenledikçe pdf koymuş olacağız.
Ancak, başka alanlarda ciddi eksikliklerimiz var. Bunlar bir hayli zaman alacak. O yüzden bu seneki sınava yetişemeyecek.