Soru Sor sayfası kullanılarak Sayıların Çözümlenmesi konusu altında Toplanan sayıları çözümleyerek rakamların değerini bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

2.SORU


3.SORU


4.SORU


5.SORU

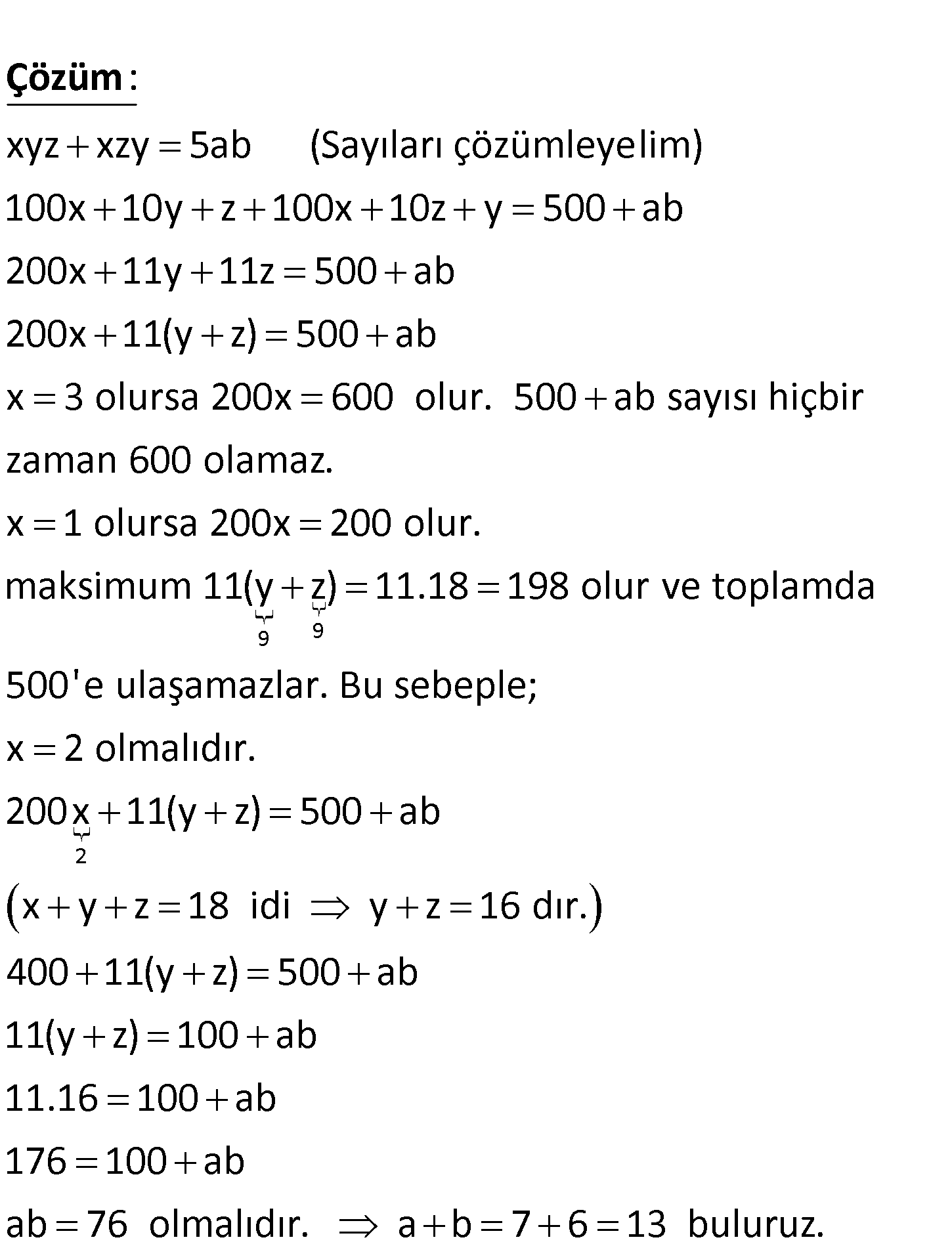
6.SORU


7.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
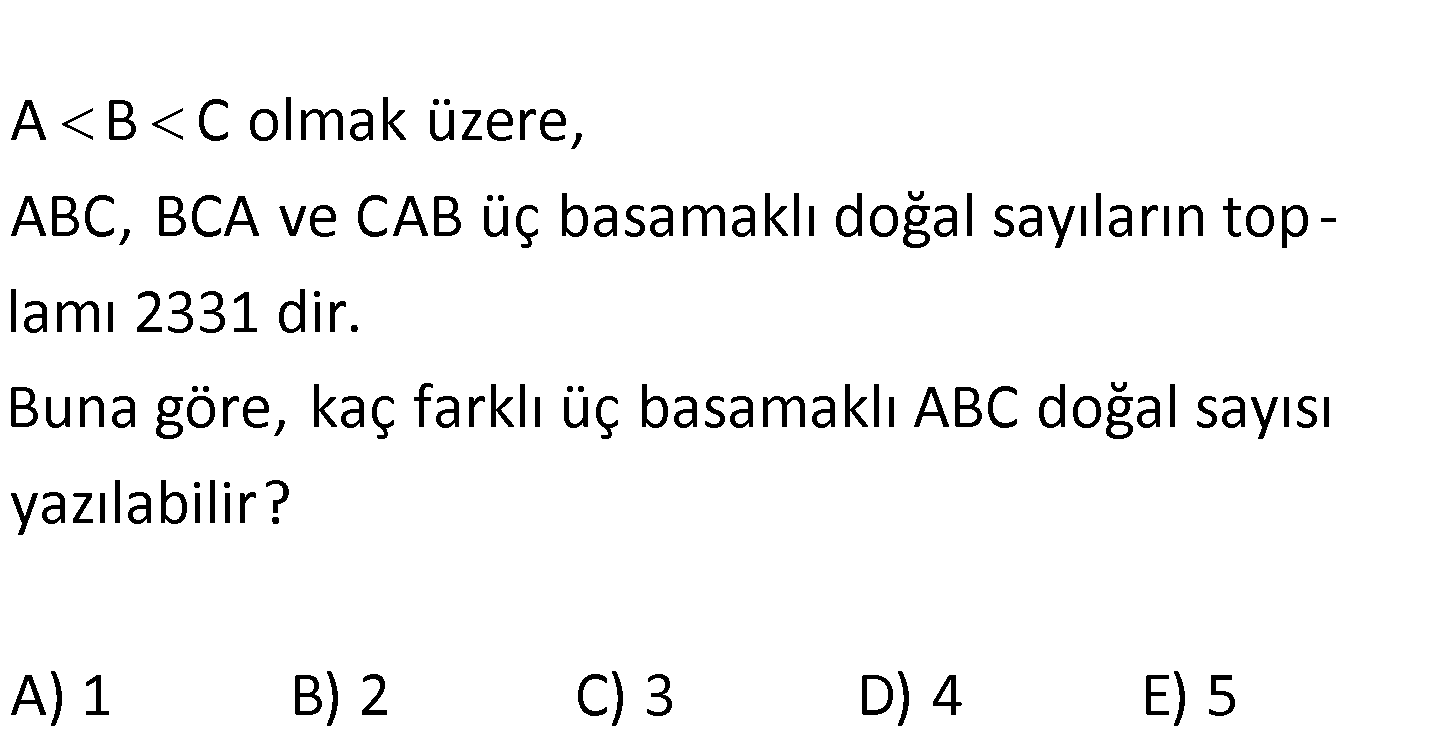
ABC olmak üzere,ABC, BCA ve CBA üç basamaklı doğal sayıların top-lamı 2331 dir.Buna göre, kaç farklı üç basamaklı ABC doğal sayısıyazılabilir?A) 1B) 2C) 3D) 4E) 5 www.matematikkolay.net ABC 100A 10B C BCA 100B 10C A : Çözüm 2331 CAB 100C 10A C ABC BCA CAB 111A 111B 111C ABC BCA CAB 111(A B C) 2331 2331 111(A B C) A B C 21 111 A B C 21 buluruz. Şimdi A,B,C için değerler verelim. C 9 ve B 8 için A 21-9 -8 4 bulun ur. C 9 ve B 7 için A 21-9 -7 5 bulunur. C 9 ve B 6 için A 21-9 -6 6 bulunur. (A B olmalı bu olmaz) C 8 ve B 7 için A 21-8 -7 6 bulunur. Bundan sonra değer vermeye çalışsak A B C sağlanmaz. ABC için 489 , 579 , 678 şeklinde 3 farklı değer buluruz. Doğru Cevap : C Şıkkı 2
a Sıfırdan farklı a, b ve c rakamları istenildiği kadar kullanarak yazılabilecek tüm iki basamaklı s yılar toplanıyor. Bu toplamın a b c toplamına bölümünden elde edilen bölüm kaçtır? A) 35 B) 33 C) 28 D) 24 E) 18 www.matematikkolay.net 10a a 10a b 10b b 10b a 10c c 10a c 10c a Tüm iki basamaklı sayıların toplamı; aa ab bb ba cc ac c : a Çözüm 10b c 10c b bc cb (Her sayı 3 ker e onlar basamağında, 3 kere de birler basamağında yer alıyor.) 33a 33b 33c dir. 33(a b c) Bu ifadeyi a b c’ye bölersek; 33 elde ederiz. 31
m K ve L rakamları ile yazılabilecek tüm iki basa aklı doğal sayıların toplamı 198 olduğuna göre, K L toplamı kaçtır? KK LL KL LK 198 ise sayıları çözümleyerek açalım. 10K K 10L L 10K L 10L K 198 22K 22L 198 22 : Çözüm (K L) 198 K L 9 buluruz. 32
A ve B rakamları kullanılarak yazılabilecek iki basamaklı tüm doğal sayıların toplamı 264 olduğun a göre, bu koşula uyan rakamları farklı iki basamaklı A) 5 k B) B 6 C y ) ı v 7 r D ı ) ? 8 a E s ) s 9 d A a ı ç a r AB BA AA BB 264 Sayıları çözümleyerek yazalım. 10A B 10B A 10A A 10B B 264 22A 22B 264 2 : 2 Çözüm (A B) 264 12 3 9 4 8 5 7 6 6 7 5 8 4 9 3 A B 12 dir. Burada 7 farklı durum var. Rakamları farklı dendiği için A 6 ve B 6’yı alamayız. Geriye 6 farklı durum kalır. Cevap: 6 41
xyz xzy 5ab Yukarıda verilen toplama işleminde x y z 18 olduğuna göre, a b toplamı kaçtır? A) 11 B) 12 C) 13 D) 14 E) 15 www.matematikkolay.net xyz xzy 5ab (Sayıları çözümleyelim) 100x 10y z 100x 10z y 500 ab 200x 11y 11z 500 ab 20 x : 0 Çözüm 9 9 2 11(y z) 500 ab x 3 olursa 200x 600 olur. 500 ab sayısı hiçbir zaman 600 olamaz. x 1 olursa 200x 200 olur. maksimum 11(y z) 11.18 198 olur ve toplamda 500’e ulaşamazlar. Bu sebeple; x 2 olmalıdır. 200x 11(y z) 500 ab x y z 18 idi y z 16 dır. 400 11(y z) 500 ab 11(y z) 100 ab 11.16 100 ab 176 100 ab ab 76 olmalıdır. a b 7 6 13 buluruz. 45
a ve b sıfırdan ve birbirinden farklı rakamlardır. a ve b rakamları kullanılarak yazılan tüm iki basamaklı sayıların toplamı 242 olduğuna göre, a.b çarpımı en çok kaçtır? A) 30 B) 28 C) 24 D) 18 E) 11 ab aa bb ba sayılarının toplamı 242 imiş. ab aa bb ba 242 10a b 11a 11b 10b a 242 22a 22b 242 2 : Çözüm 2(a b) 242 a b 11 dir. Çarpımları en büyük olması için birbirine yakın seçmeliyiz. 5 ve 6 seçelim. a.b 5.6 30 dur. www.matematikkolay.net 51
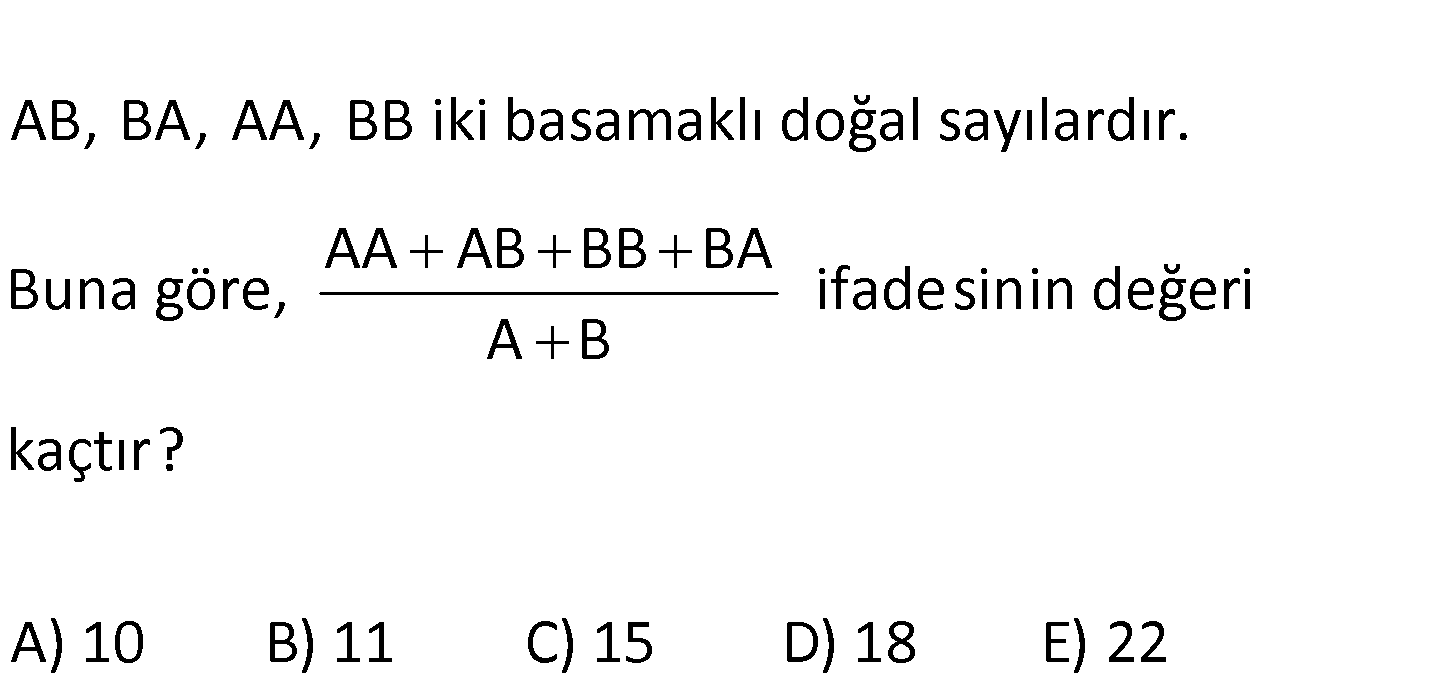
AB, BA, AA, BB iki basamaklı doğal sayılardır. AA AB BB BA Buna göre, ifadesinin değeri A B kaçtır? A ) 10 B) 11 C) 15 D) 18 E) 22 www.matematikkolay.net 10A A 10A B 10B B 10B A Sayıları çözümleyerek yazalım. AA AB BB BA A B 10A A 10A B 10B B 10B A : A B Çözüm 22A 22B A B 22 A B A B 22 buluruz. 63


1.soruda Konya’yı sorup Kenya’yı cozmussunuz haberiniz olsun…
Uyarınız için teşekkürler. 3.sayı “CAB” olacağına “CBA” yazılmış. Şimdi düzelttik.