Soru Sor sayfası kullanılarak Özel Üçgenler konusu altında 30-30-120 üçgeni ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

2.SORU

3.SORU

4.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
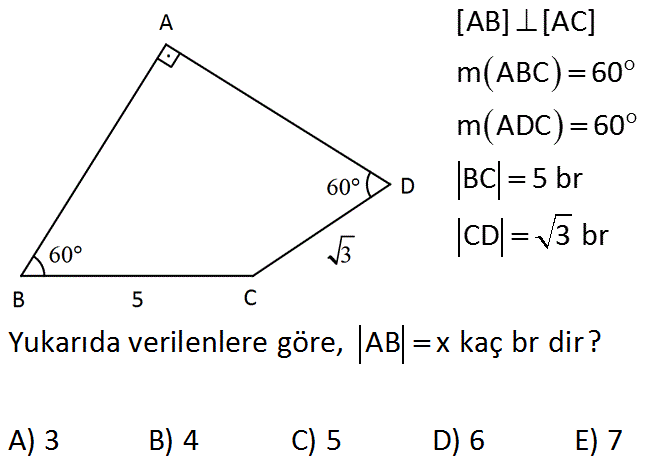
www.matematikkolay.net [AB] [AC] m ABC 60 m ADC 60 BC 5 br CD 3 br Yukarıda verilenlere göre, AB x kaç br dir? A) 3 B) 4 C) 5 D) 6 E) 7 : Çözüm Dik üçgeni D ve C köşelerinden uzatarak tamamlarsak; E açısı 30 olur. CDE üçgeni 30 – 120 – 30 üçgeni olur. 30 ‘nin karşısında a var sa 120 ‘nin karşısında a 3 olur. CE 3. 3 3 br olur. ABE üçgeninde BE 8 br old uğuna göre 8 AB 4 br olur. (30 -60 -90) 2 10
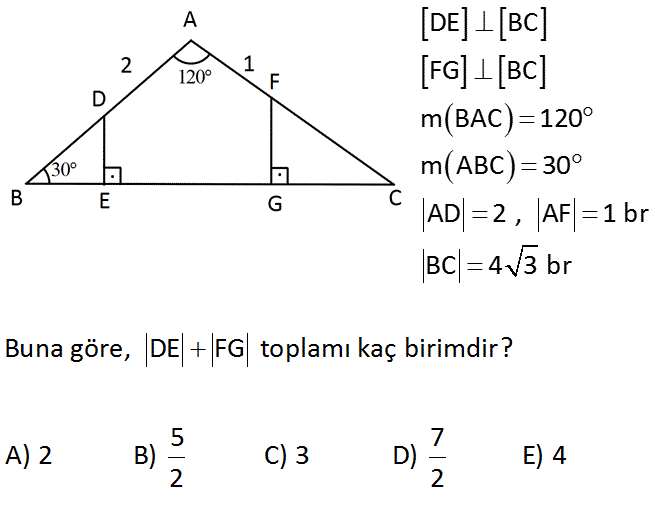
DE BC FG BC m BAC 120 m ABC 30 AD 2 , AF 1 br BC 4 3 br Buna göre, DE FG toplamı kaç birimdir? 5 7 A) 2 B) C) 3 D) E) 4 2 2 : Çözüm www.matematikkolay.net m(ACB) 180 120 30 180 150 30 dir. O halde ABC üçgeni bir 30 -30 -120 üçgenidir. 120’nin karşısı 4 3 birim ise, 30 ‘nin karşısı 4 birimdir. AB 4 ise BD 2 birimdir. AC 4 is e FC 3 birimdir. Hem DBE üçgeni hem de FGC birer 30 -60 -90 üçgenidir. 30’un karşısı hipotenüsün yarısı olduğundan; 2 3 DE 1 ve GF dir. 2 2 3 5 Toplamları 1 buluruz. 2 2 46
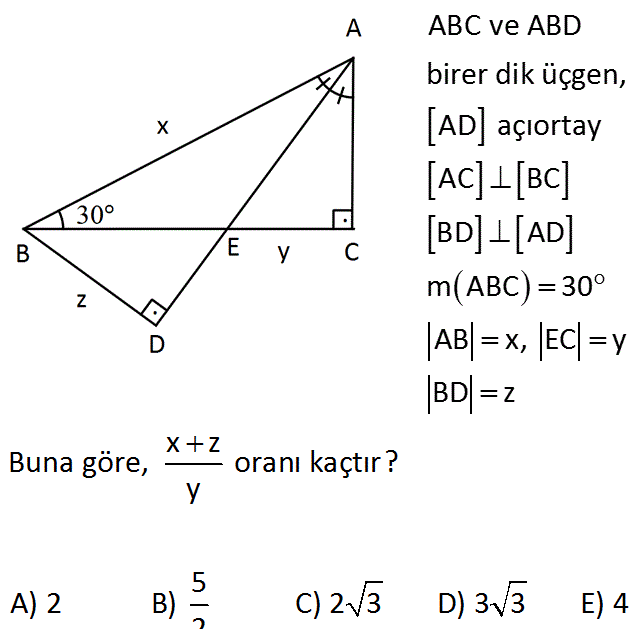
ABC ve ABD birer dik üçgen, AD açıortay AC BC BD AD m ABC 30 AB x, EC y BD z www.matematikkolay.net x z Buna göre, oranı kaçtır? y 5 A) 2 B) C) 2 3 D) 3 3 E) 4 2 : Çözüm m(BAC) 60 dir. Açıortay açıları 30’ar derece olur. AEC üçgeni bir 30 -60 -90 üçgenidir. 30’un karşısı y ise, 90’ın karşısı 2y dir. |AE| 2y ABE üçgeni bir 30 -30 -120 üçgenidir. x 2y 3 tür. m(EBD) 180 90 30 3 0 30 dir. O halde; EBD üçgeni bir 30 -60 -90 üçgenidir. |BE| 2y ise |ED| y ve z y 3 tür. Buna göre; x z 2y 3 y 3 3y 3 3 3 buluruz. y y y 31
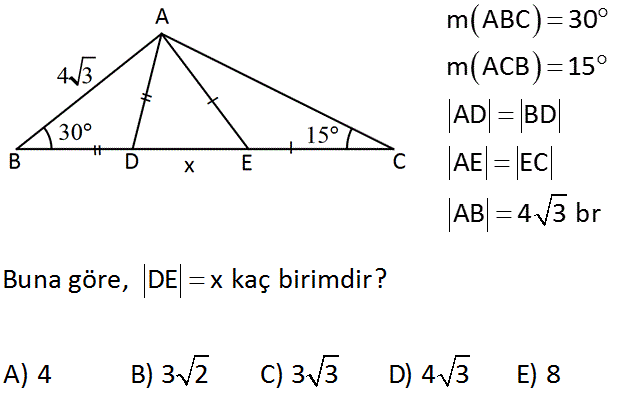
m ABC 30 m ACB 15 AD BD AE EC AB 4 3 br Buna göre, DE x kaç birimdir? A) 4 B) 3 2 C) 3 3 D) 4 3 E) 8 Çözüm: www.matematikkolay.net BD AD olduğundan m(DAB) 30 dir. ABD üçgeninde iki iç açının toplamı 60 olduğundan, diğer köşenin dış açısı 60 dir. m(ADE) 60 dir. ABD üçgeni bir 30 -30 -120 üçgeni olduğundan; 30’un karşısındaki ke narlar 4’er birimdir. AE EC olduğundan m(DAB) 15 dir. AEC üçgeninde iki iç açının toplamı 30 olduğundan, diğer köşenin dış açısı 30 dir. m(AED) 30 dir. O halde ADE üçgeni bir 30 -60 -90 üçgenidir. 3 0’un karşısı 4 birim ise 90 nin karşısı 8 birimdir. x 8 buluruz. 47


Basit birşey olabilir 120 30 30 uckeninin uzun kenarı 50 cm olursa eşit kenarları kaç cm olur cevap verirseniz sevinirim