Soru Sor sayfası kullanılarak Öklit Bağıntıları konusu altında Öklit Dik Kenar ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
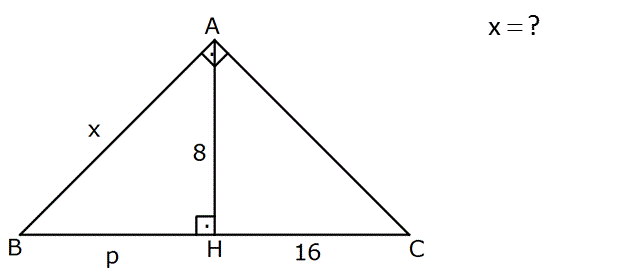
1.SORU
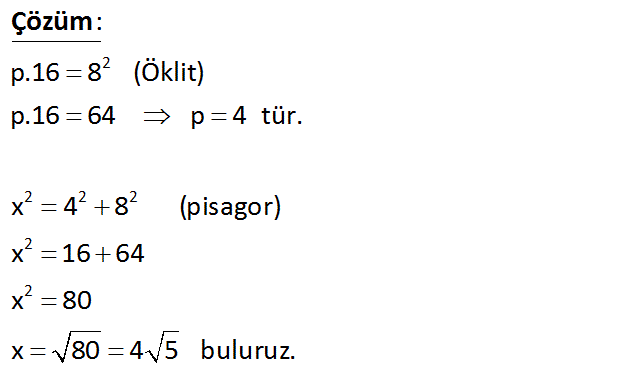
2.SORU
3.SORU
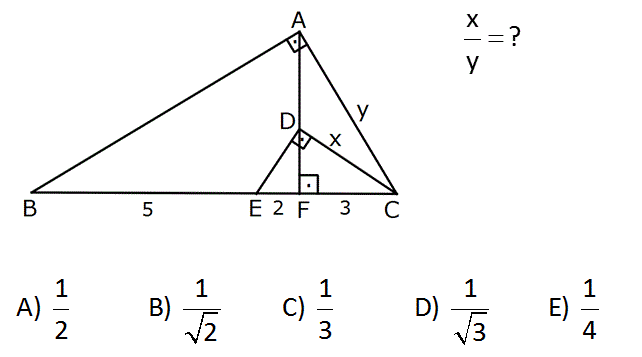
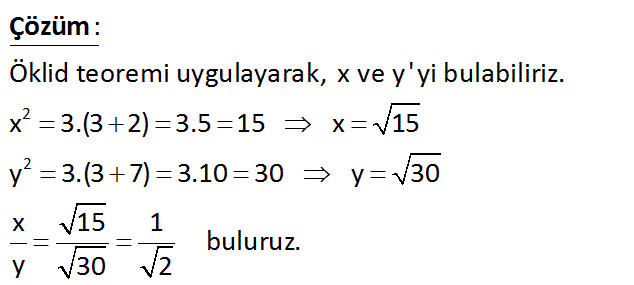
4.SORU

5.SORU
6.SORU

7.SORU
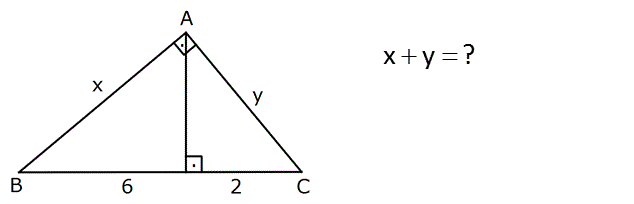

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
x ? 2 2 2 2 2 2 p.16 8 (Öklit) p.16 64 p 4 tür. x 4 8 (pisagor) x 16 64 x 80 x 80 4 5 buluruz. : Çözüm www.matematikkolay.net 5
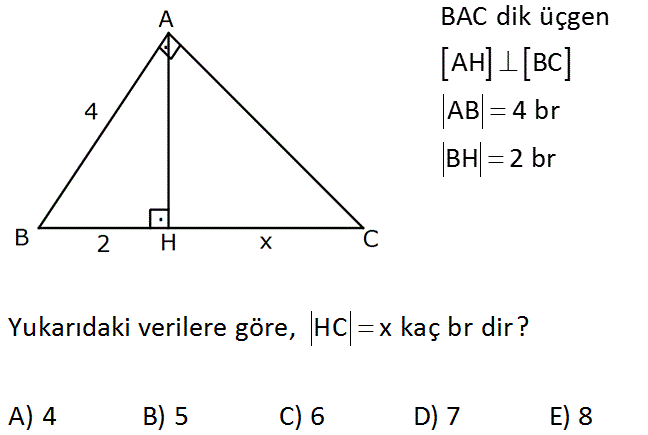
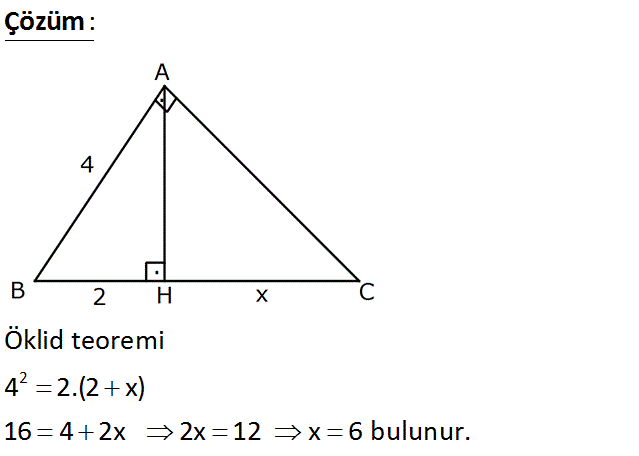
www.matematikkolay.net BAC dik üçgen AH BC AB 4 br BH 2 br Yukarıdaki verilere göre, HC x kaç br dir? A) 4 B) 5 C) 6 D) 7 E) 8 : Çözüm 2 Öklid teoremi 4 2.(2 x) 16 4 2x 2x 12 x 6 bulunur. 7
x ? y 1 1 1 1 1 A) B) C) D) E) 2 2 3 3 4 2 2 Öklid teoremi uygulayarak, x ve y’ yi bulabiliriz. x 3.(3 2) 3.5 15 x 15 y 3.(3 7) 3.10 30 y 30 x 15 1 buluruz. y 3 2 : 0 Çözüm www.matematikkolay.net 9
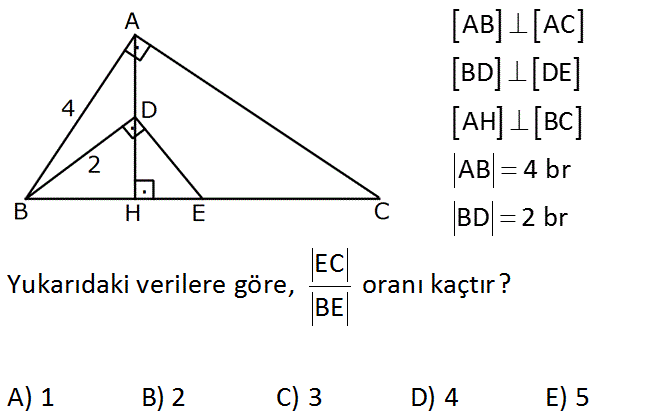
www.matematikkolay.net AB AC BD DE AH BC AB 4 br BD 2 br EC Yukarıdaki verilere göre, oranı k A) 1 B) 2 C) 3 D) 4 E) 5 açt ır? BE : Çözüm 2 2 Öklit teoremindeki yan dik kenarı bulan formülü kullanacağız. |BD| a.(a b) a(a b) 4 tür. |AB| a.(a b c) a(a b c) 16 dır. Taraf tarafa oranlayalım. a (a b) a 4 (a b c) 1 16 4 k a b 1 a b c 4 a b k dersek , a b c 4k olur. c 3k olur. |EC| c 3k 3 buluruz. |BE| a b k www.matematikkolay.net 11
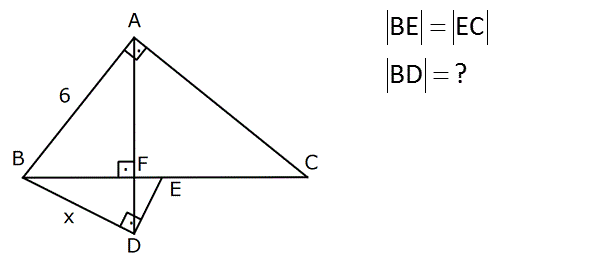
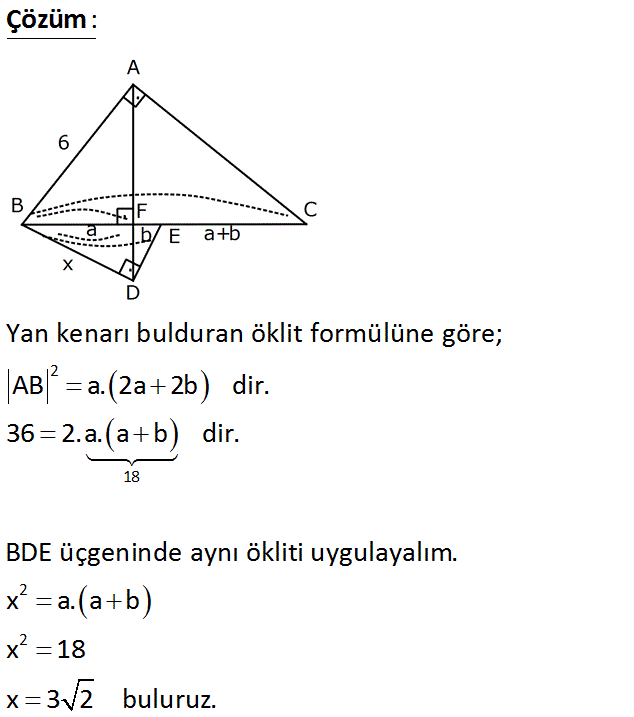
BE EC BD ? www.matematikkolay.net : Çözüm 2 18 2 2 Yan kenarı bulduran öklit formülüne göre; AB a. 2a 2b dir. 36 2.a. a b dir. BDE üçgeninde aynı ökliti uygulayalım. x a. a b x 18 x 3 2 buluruz. 19
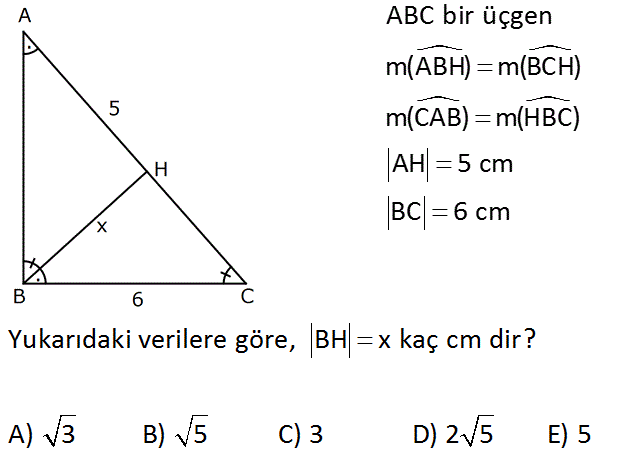
ABC bir üçgen m(ABH) m(BCH) m(CAB) m(HBC) AH 5 cm BC 6 cm Yukarıdaki verilere göre, BH x kaç cm dir? A) 3 B) 5 C) 3 D) 2 5 E) 5 www.matematikkolay.net Çözüm: 2 2 Eşit açıları harflendirelim. ABC üçgeninin iç açıları toplamına göre; 2a 2b 180 a b 90 dir. Bu sebeple m(ABC) 90 ve m(BHC) 90 olur. Yan dik kenarı veren öklit formülüne göre; BC CH . CA 6 y. y 5 36 2 2 2 2 2 2 y 5y 0 y 5y 36 0 y 9 y 4 y 4 tür. BHC üçgeninde pisagordan x y 36 x 16 36 x 20 x 2 5 cm buluruz. 20
www.matematikkolay.net x y ? 2 2 2 2 2 Öklit teoremineki yan dik kenarları bulan formülü kullanalım. y 2 2 6 y 16 y 4 tür. x 6 6 2 x 6.8 x 48 x 4 3 tür. x y 4 3 4 buluruz : . Çözüm

