Soru Sor sayfası kullanılarak Logaritma konusu altında Logaritma Tanım Aralığı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
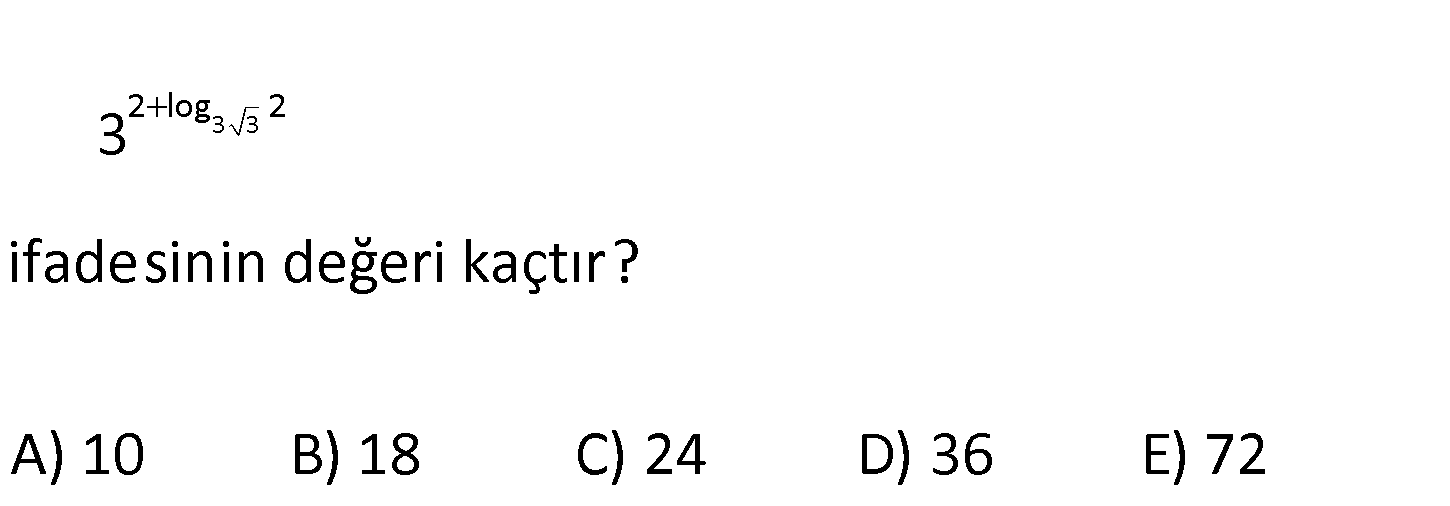
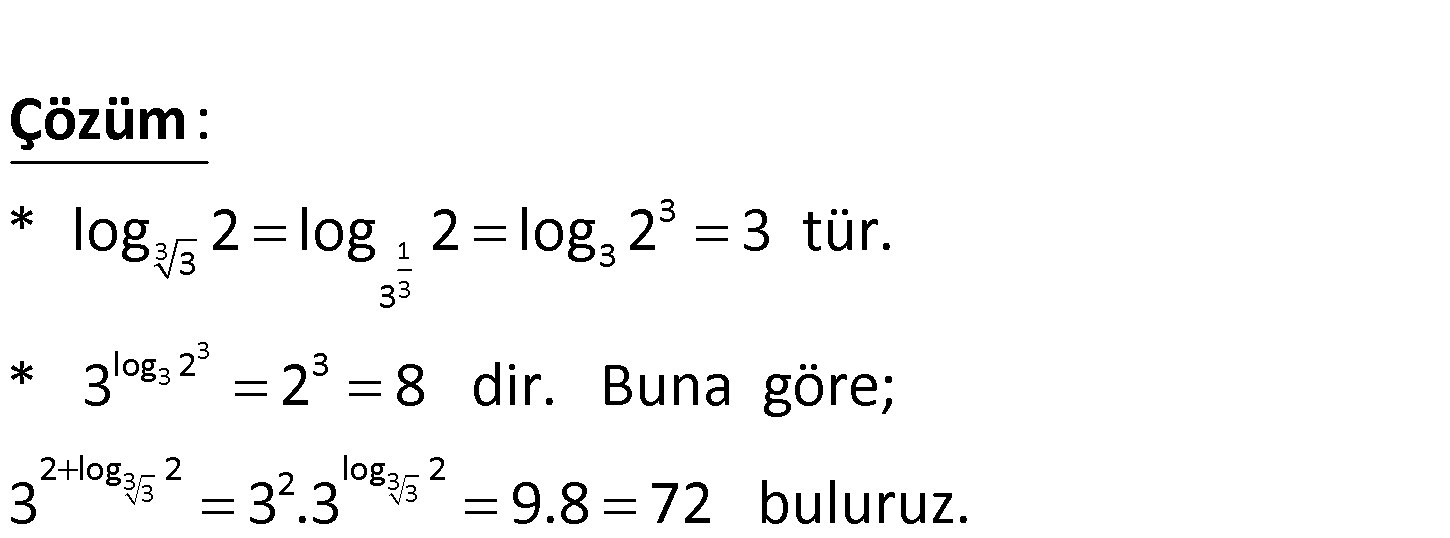
2.SORU
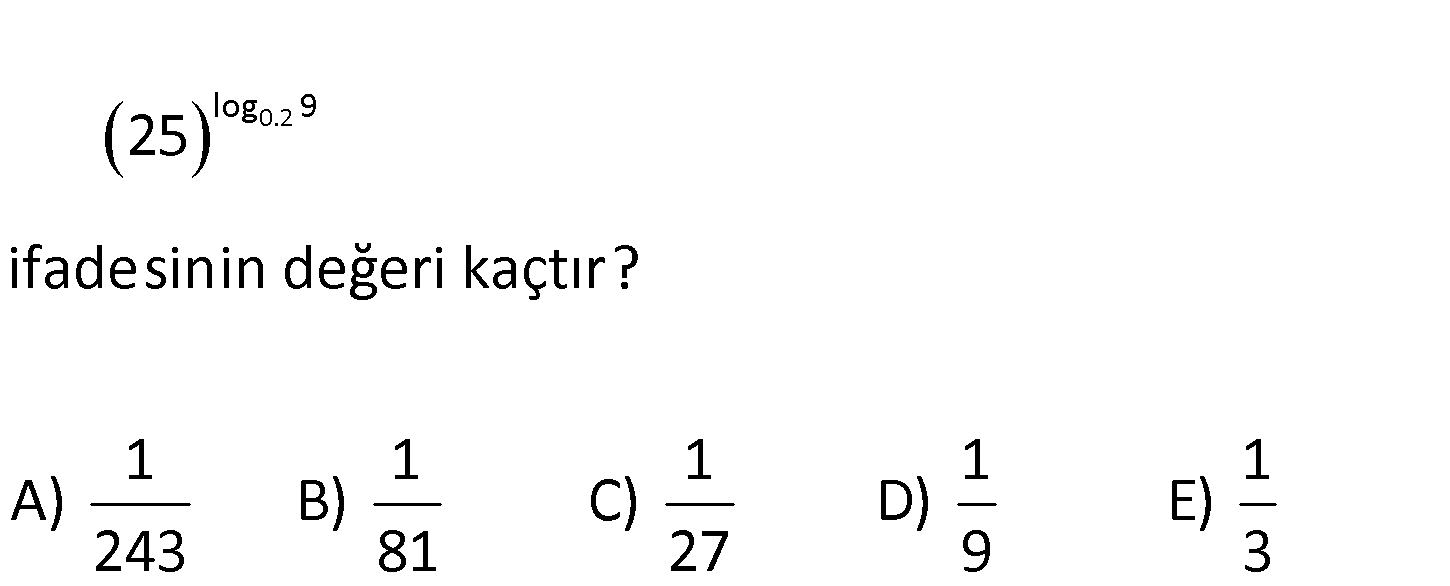
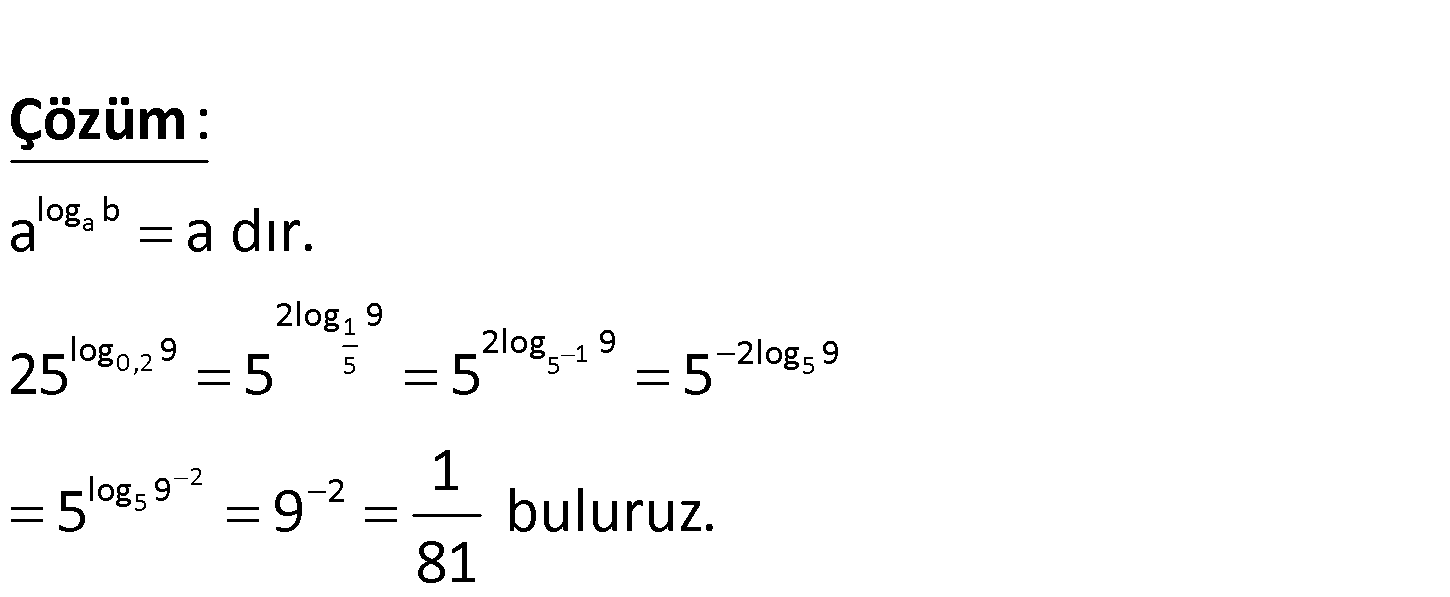
3.SORU
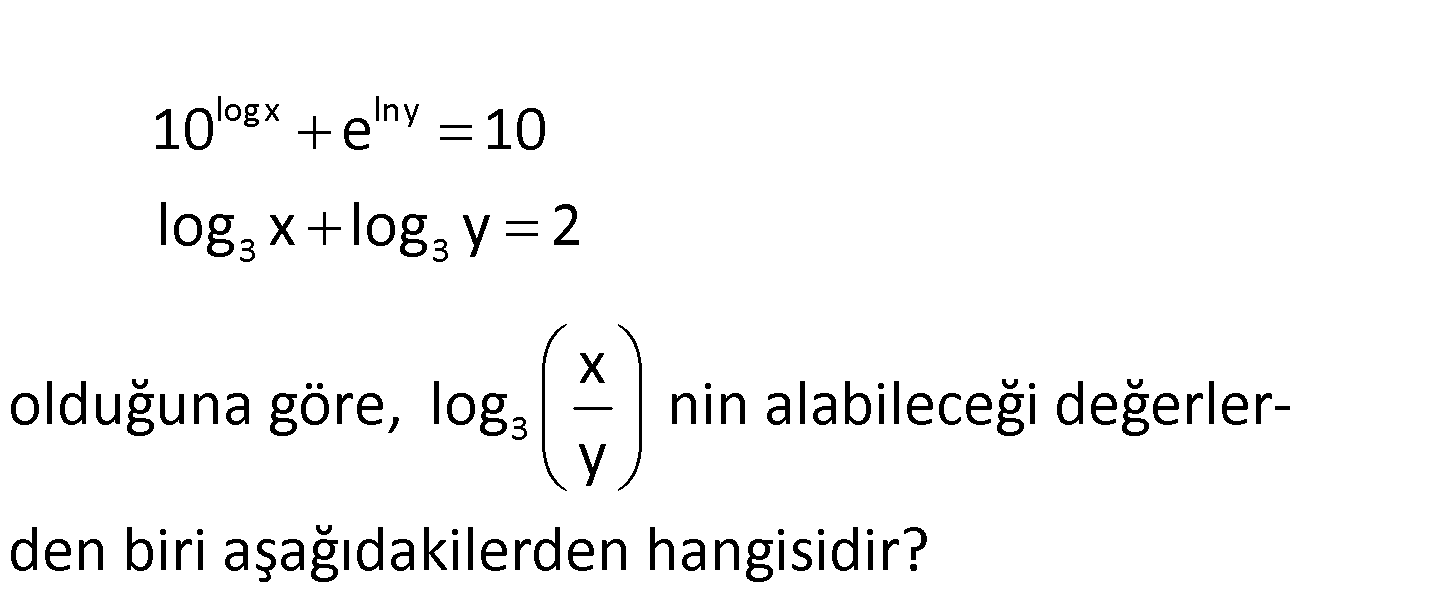
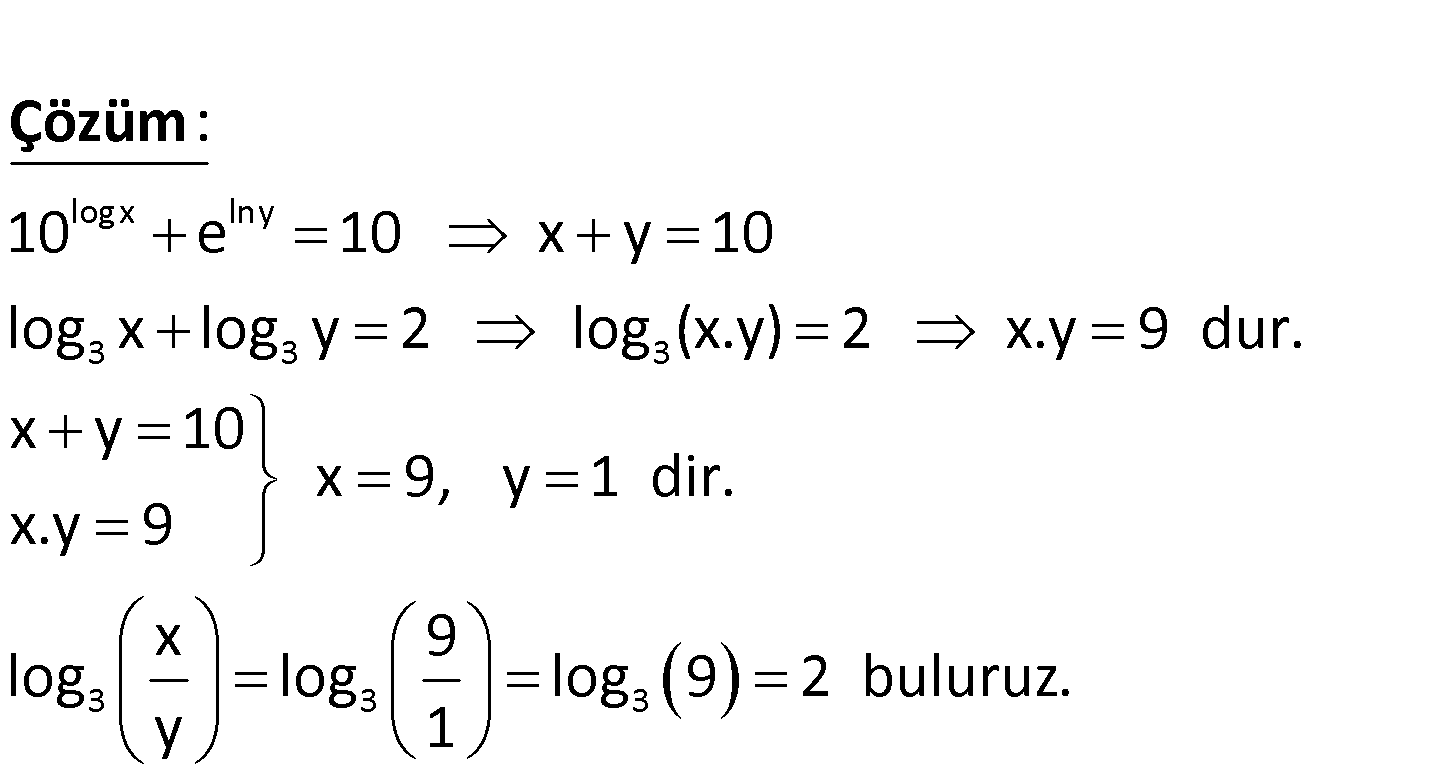
4.SORU
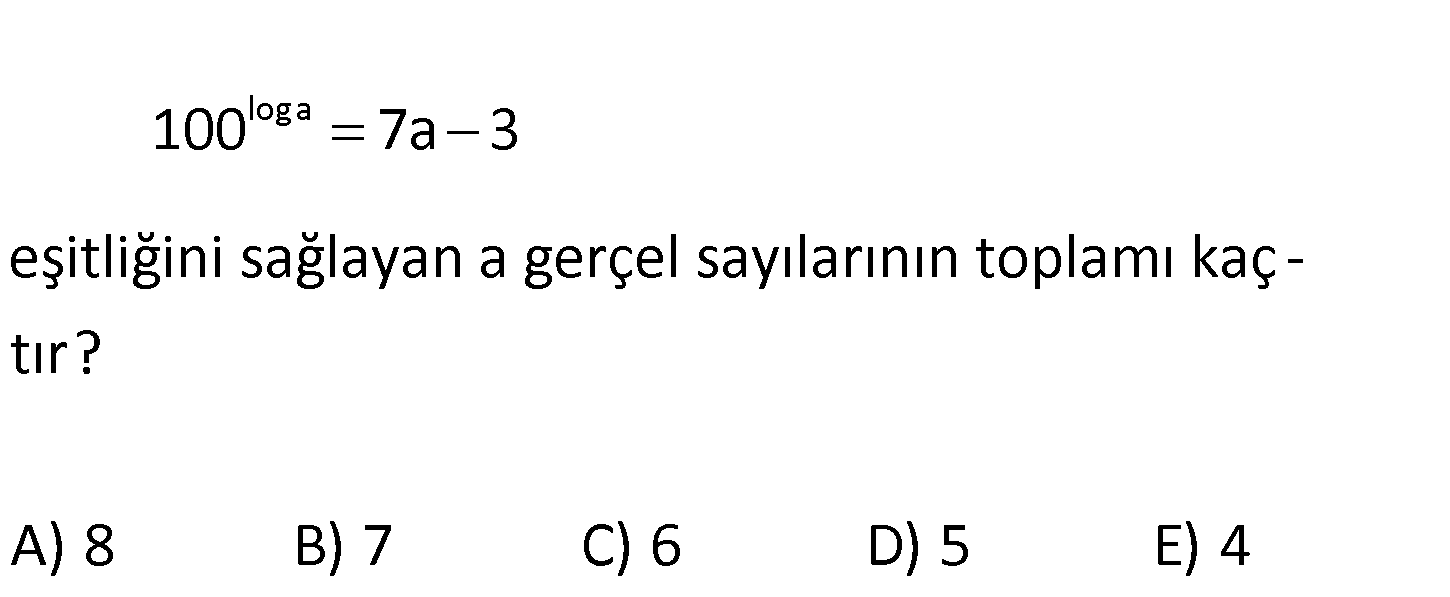
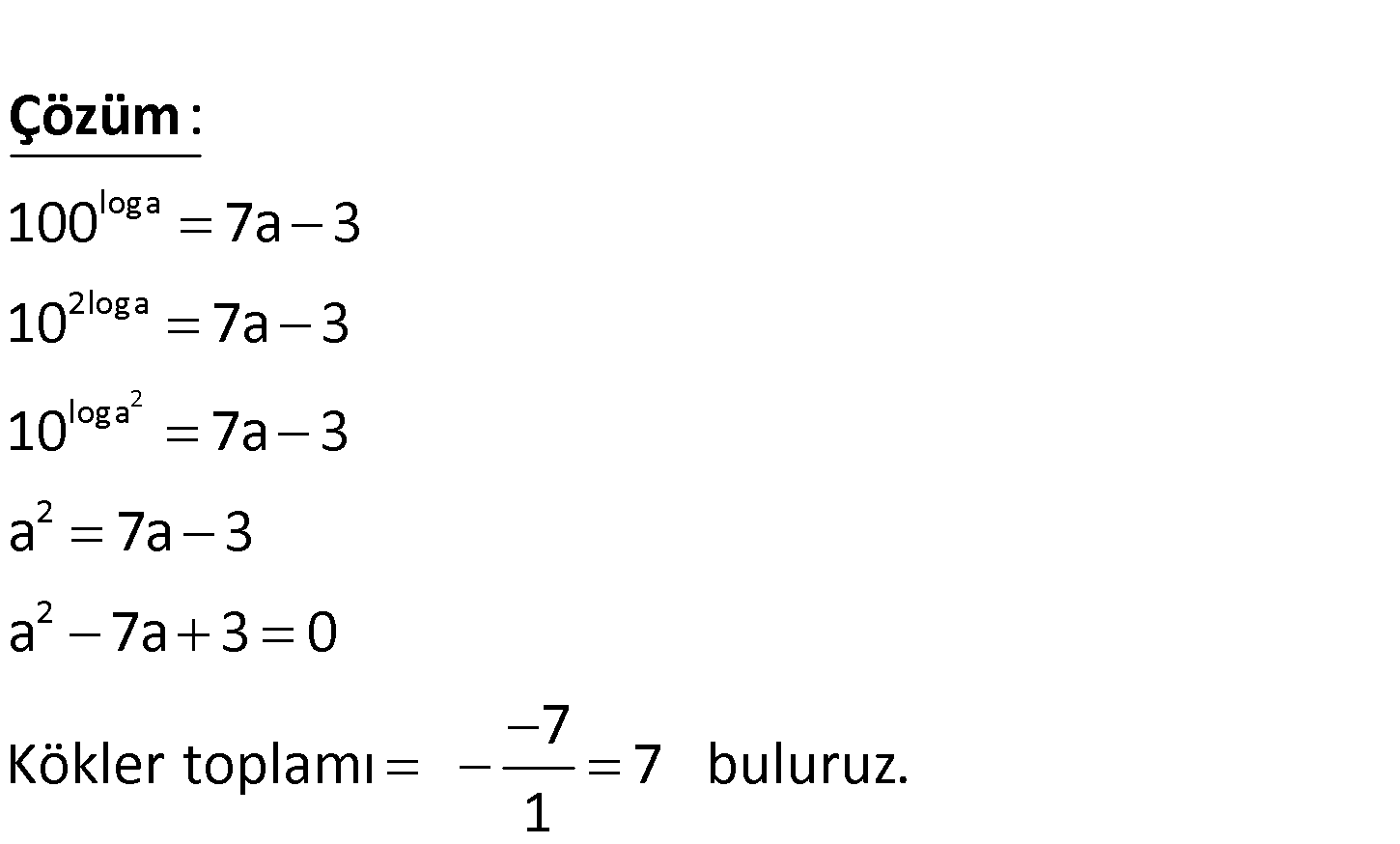
5.SORU
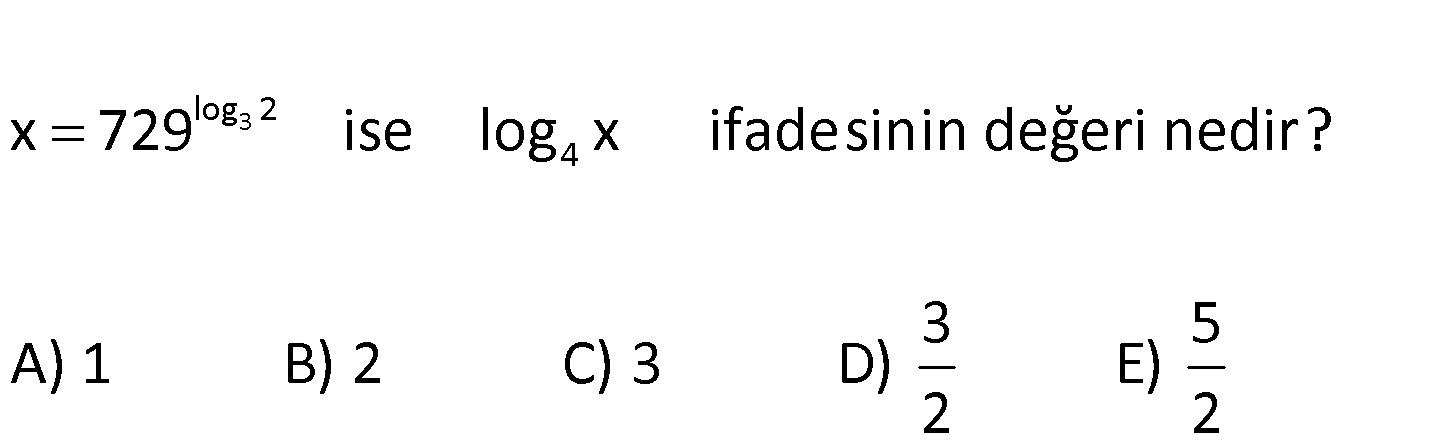
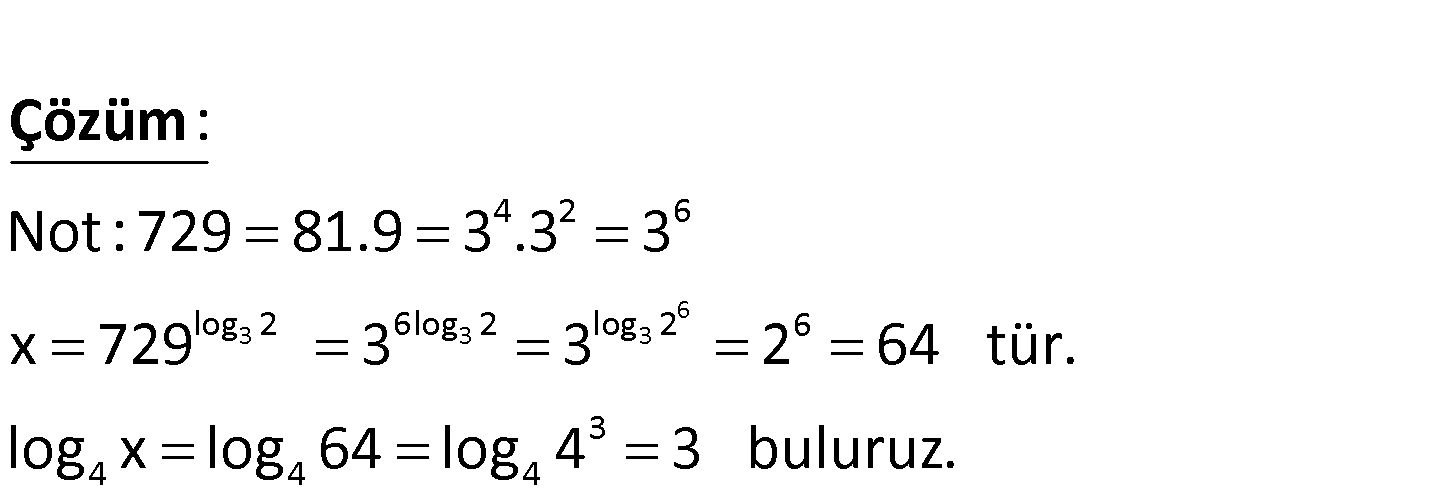
6.SORU
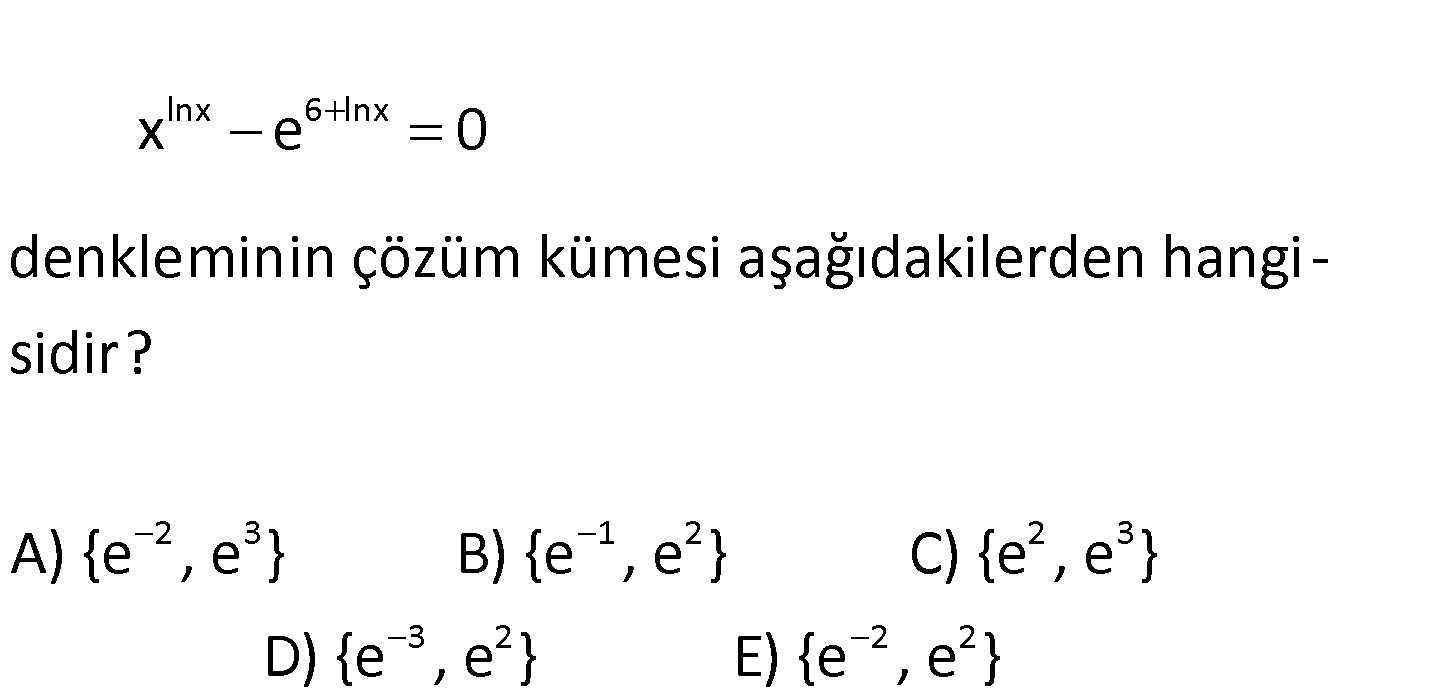

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 3 2 log 2 3 ifadesinin değeri kaçtır? A) 10 B) 18 C) 24 D) 36 E) 72 3 1 3 3 3 3 3 3 3 3 3 3 3 log 2 3 2 log 2 2 log 2 * log 2 log 2 log 2 3 tür. * 3 2 8 dir. Buna göre; 3 3 .3 . : 9 Çözüm 8 72 buluruz. www.matematikkolay.net 17
www.matematikkolay.net log0.2 9 25 ifadesinin değeri kaçtır? 1 1 1 1 1 A) B) C) D) E) 243 81 27 9 3 a 1 0 ,2 5 5 1 5 2 5 log b 2log 9 log 9 2log 9 2log 9 log 9 2 a a dır. 25 5 5 5 1 5 9 buluruz. 81 : Çözüm 52
logx lny 3 3 3 10 e 10 log x log y 2 x olduğuna göre, log nin alabileceği değerle y rden biri aşağıdakilerden hangisidir? www.matematikkolay.net logx lny 3 3 3 10 e 10 x y 10 log x log y 2 log (x.y) 2 x.y 9 dur. x y 10 x 9, y x : .y 9 Çözüm 3 3 3 1 dir. x 9 log log log 9 2 buluruz. y 1 90
loga 100 7a 3 eşitliğini sağlayan a gerçel sayılarının toplamı kaç – tır? A) 8 B) 7 C) 6 D) 5 E) 4 2 loga 2loga loga 2 2 100 7a 3 10 7a 3 10 7a 3 a 7a 3 a 7a 3 0 7 Kökler toplamı 7 buluruz 1 : . Çözüm www.matematikkolay.net 91
log3 2 4 x 729 ise log x ifadesinin 3 5 A) 1 B) 2 C) 3 D) d E) 2 eğeri ned r? 2 i 6 3 3 3 4 2 6 log 2 6log 2 log 2 6 3 4 4 4 Not : 729 81.9 3 .3 3 x 729 3 3 2 64 tür. log x log 64 log 4 3 bulur : Çözüm uz. 124
lnx 6 lnx 2 3 1 2 x e 0 denkleminin çözüm kümesi aşağıdakilerden hangi – sidir? A) {e , e } B) {e , e 2 3 3 2 2 2 } C) {e , e } D) {e , e } E) {e , e } www.matematikkolay.net lnx 6 lnx lnx lnx 6 lnx 1 6 x e 0 Not : e x tir. x e x 0 x x e 0 lnx in içi 0 olamayacağı için x 0 : Çözüm lnx 1 6 lnx 1 2 3 2 olamaz. x e olur. Her iki tarafın ln’i alalım. lnx 6 lnx 1 lnx 6 lnx lnx 6 0 lnx 3 lnx 2 0 x e ve x e dir. 146

