Üstel Fonksiyon
a, 1 den farklı pozitif bir reel sayı olsun. ![]() ,
, ![]() şeklinde tanımlanan fonksiyona üstel fonksiyon denir. Burada a sayısı üstel fonksiyonun tabanı ve x üs olarak adlandırılır.
şeklinde tanımlanan fonksiyona üstel fonksiyon denir. Burada a sayısı üstel fonksiyonun tabanı ve x üs olarak adlandırılır.
Örnek 1: ![]() üstel fonksiyondur. Doğru mu? Yanlış mı?
üstel fonksiyondur. Doğru mu? Yanlış mı?
| | |
Açıklaması
3 sayısı pozitif ve 1 den farklıdır. Dolayısıyla ![]() bir üstel fonksiyondur.
bir üstel fonksiyondur.
![]() üstel fonksiyondur. Doğru mu? Yanlış mı?
üstel fonksiyondur. Doğru mu? Yanlış mı?
| | |
Açıklaması
Tabandaki sayı sabit bir sayı olmalı, değişken olmamalı. O yüzden üstel bir fonksiyon değildir.
![]() üstel bir fonksiyondur. Doğru mu? Yanlış mı?
üstel bir fonksiyondur. Doğru mu? Yanlış mı?
| | |
Açıklaması
![]()
![]() sayısı da pozitif ve 1 den farklıdır. Dolayısıyla üstel bir fonksiyondur.
sayısı da pozitif ve 1 den farklıdır. Dolayısıyla üstel bir fonksiyondur.
![]() üstel bir fonksiyondur. Doğru mu? Yanlış mı?
üstel bir fonksiyondur. Doğru mu? Yanlış mı?
| | |
Açıklaması
5 sayısı pozitif ve 1 den farklıdır. Ayrıca x değişkeni sadece 5’in üstündedir. 2 ise fonksiyonu 2 birim yukarı öteleyecektir. Üstel bir fonksiyon olmasını engellemez. Dolayısıyla üstel bir fonksiyondur.
![]() üstel bir fonksiyondur. Doğru mu? Yanlış mı?
üstel bir fonksiyondur. Doğru mu? Yanlış mı?
| | |
Açıklaması
Üstel fonksiyonda taban 1 olamaz. Çünkü üstel fonksiyonlar birebir ve örten olmak zorundadır. Tersi logaritmayı oluşturacaktır. 1’in tüm kuvvetleri 1 olduğundan tersi alınması imkansızdır. Dolayısıyla üstel bir fonksiyon değildir.
Üstel Fonksiyonda Artanlık Azalanlık
![]() şeklinde bir üstel fonksiyonda,
şeklinde bir üstel fonksiyonda,
![]() ise artan fonksiyon
ise artan fonksiyon
![]() ise azalan fonksiyondur.
ise azalan fonksiyondur.
Not: Üstel fonksiyonlar birebir ve örten fonksiyonlardır.
Örnek 2: ![]() ,
, ![]() fonksiyonu azalan bir fonksiyondur. Doğru mu? Yanlış mı?
fonksiyonu azalan bir fonksiyondur. Doğru mu? Yanlış mı?
| | |
Açıklaması
4 sayısı 1 den büyük olduğu için artan bir fonksiyondur.
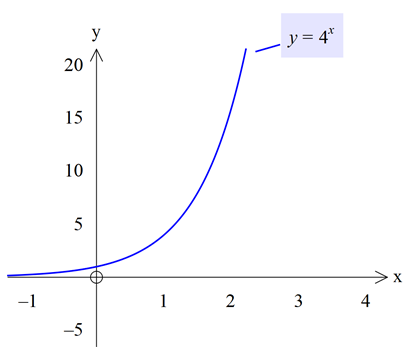
![]() ,
,![]() fonksiyonu azalan bir fonksiyondur. Doğru mu? Yanlış mı?
fonksiyonu azalan bir fonksiyondur. Doğru mu? Yanlış mı?
| | |
Açıklaması
![]() sayısı 0 ile 1 arasında olduğu için azalan bir fonksiyondur.
sayısı 0 ile 1 arasında olduğu için azalan bir fonksiyondur.
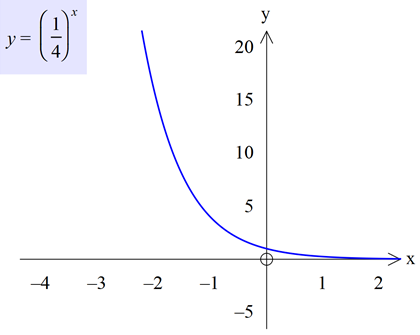
Örnek 3: ![]() fonksiyonlarının birebir ve örten olduğunu grafik çizerek gösteriniz.
fonksiyonlarının birebir ve örten olduğunu grafik çizerek gösteriniz.
Açıklaması
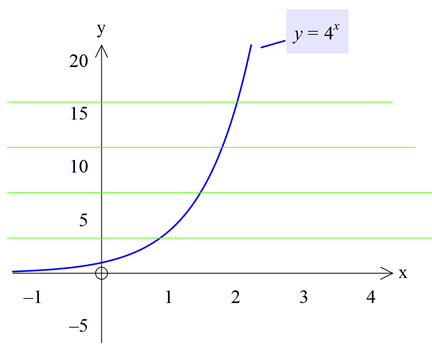
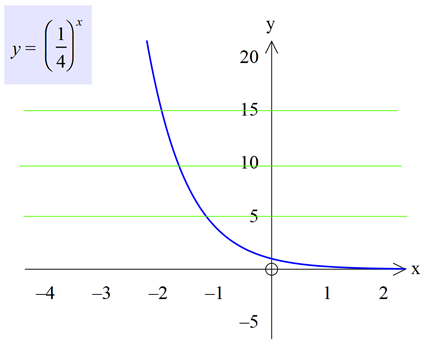
x eksenine çizilen paralel her doğru ![]() fonksiyonunun grafiğini en çok bir noktada kestiğinden f bire birdir.
fonksiyonunun grafiğini en çok bir noktada kestiğinden f bire birdir.
Yatay doğru testi ile değer kümesinin içinde çizilen yatay doğrular her noktada ![]() fonksiyonunu kestiğinden örtendir.
fonksiyonunu kestiğinden örtendir.
x eksenine çizilen paralel her doğru ![]() fonksiyonunun grafiğini en çok bir noktada kestiğinden f bire birdir.
fonksiyonunun grafiğini en çok bir noktada kestiğinden f bire birdir.
Yatay doğru testi ile değer kümesinin içinde çizilen yatay doğrular her noktada ![]() fonksiyonunu kestiğinden örtendir.
fonksiyonunu kestiğinden örtendir.
Alıştırma-1

| | | | | |
Çözüm için Tıklayınız.

LOGARİTMA FONKSİYONU
![]() olmak üzere,
olmak üzere,
![]() şeklindeki üstel fonksiyonun tersine logaritma fonksiyonu denir ve
şeklindeki üstel fonksiyonun tersine logaritma fonksiyonu denir ve ![]() şeklinde gösterilir.
şeklinde gösterilir.
![]()
![]() ifadesinde
ifadesinde ![]() sayısına
sayısına ![]() sayısının a tabanına göre logaritması denir ve ‘‘y eşittir a tabanına göre logaritma x ’’ şeklinde okunur.
sayısının a tabanına göre logaritması denir ve ‘‘y eşittir a tabanına göre logaritma x ’’ şeklinde okunur.
Örnek 4: ![]() ise x ‘i logaritma cinsinden ifade ediniz.
ise x ‘i logaritma cinsinden ifade ediniz.
Cevabı Gör
![]() dir.
dir.
![]() ise x ‘i logaritma cinsinden ifade ediniz.
ise x ‘i logaritma cinsinden ifade ediniz.
Cevabı Gör
![]()
![]() dir.
dir.
![]() ise x kaçtır?
ise x kaçtır?
Cevabı Gör
![]()
![]() dur.
dur.
![]() ise x kaçtır?
ise x kaçtır?
Cevabı Gör
![]()
![]()
![]() tür.
tür.
Logaritmanın Tanımlı Olması İçin
![]() fonksiyonunda
fonksiyonunda
![]() olmalı. Ayrıca,
olmalı. Ayrıca,
![]() olmalıdır.
olmalıdır.
Örnek 5: ![]() fonksiyonunun tanımlı olduğu aralığı bulunuz.
fonksiyonunun tanımlı olduğu aralığı bulunuz.
Çözüm için Tıklayınız.
![]() olmalı
olmalı
![]() olmalı
olmalı
![]()
Buna göre, tanım aralığı ![]() dir.
dir.
Alıştırma-2

| | | | | |
Çözüm için Tıklayınız.

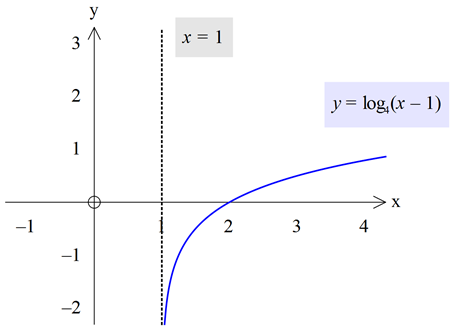
Logaritma Fonksiyonunun Grafiği
 |
 |
Yukarıdaki örneklerden anlaşılacağı üzere ![]() fonksiyonu,
fonksiyonu,
a>1 için artan
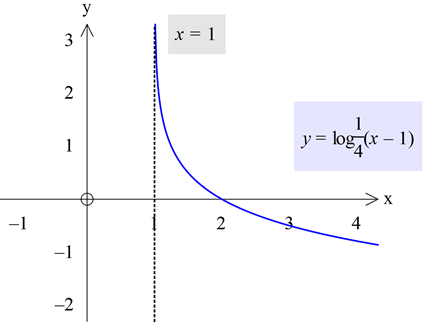
0<a<1 için azalan bir fonksiyondur.
Ayrıca x-b=0 yapan x=b değerinde fonksiyon ![]() a doğru gider.
a doğru gider.
x-b=1 yapan x değerinde de fonksiyon x eksenini keser. Çünkü 0 dışındaki tüm sayıların 0’ıncı kuvveti 1 dir.
 |
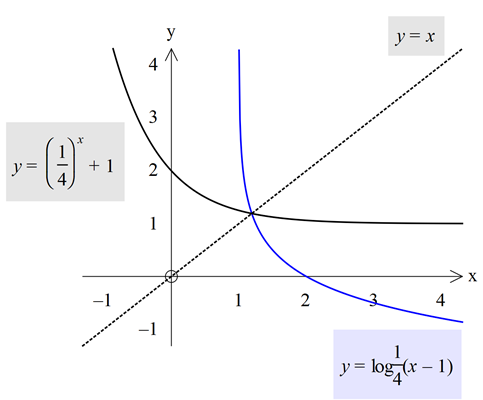 |
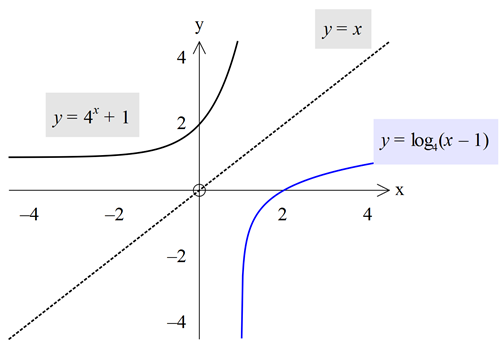
Tüm ters fonksiyonlarda olduğu gibi, logaritma ile tersi olan üstel fonksiyonun grafikleri y=x doğrusuna göre simetriktir.
Alıştırma-3
| | | | | |
Çözüm için Tıklayınız.

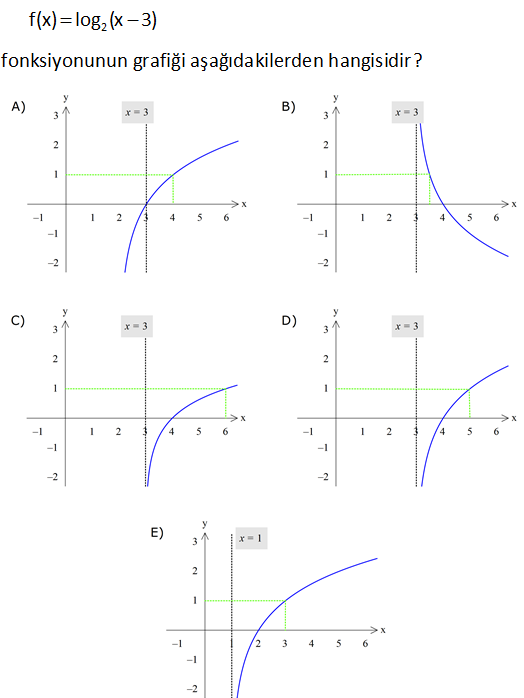
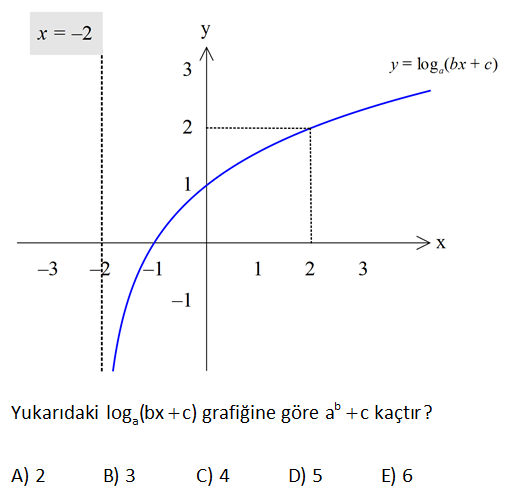
Alıştırma-4
| | | | | |
Çözüm için Tıklayınız.