BELİRLİ İNTEGRAL VE ÖZELLİKLERİ

Örnek:

Çözüm:
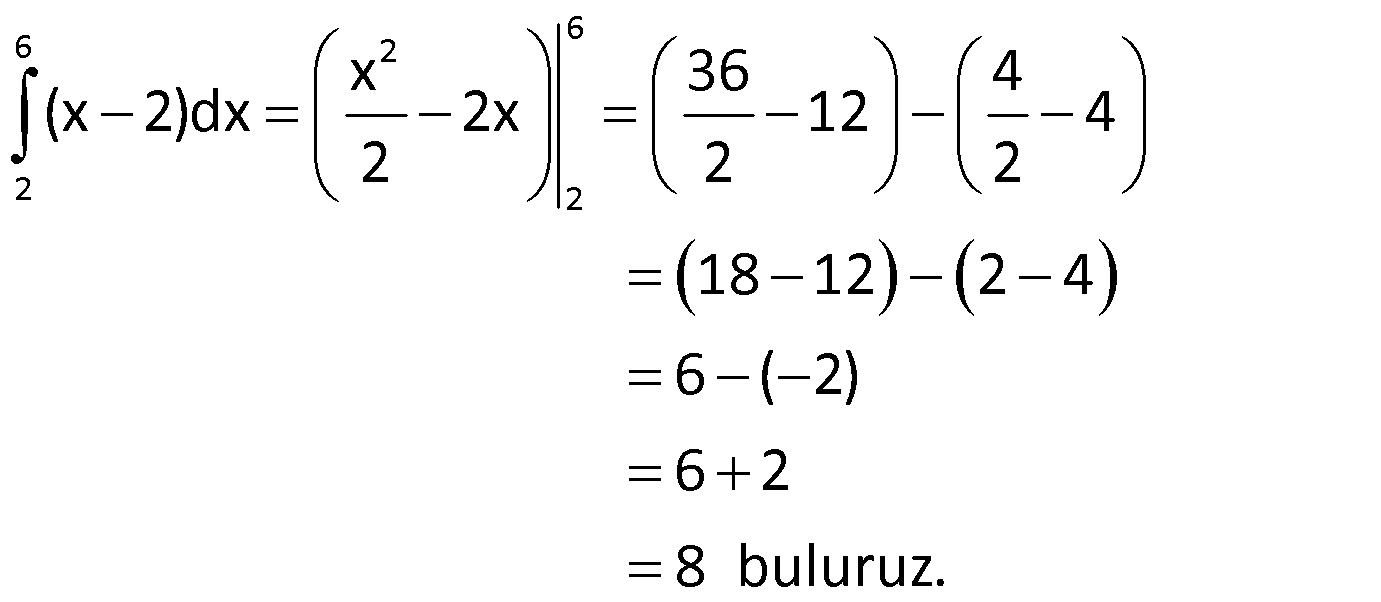
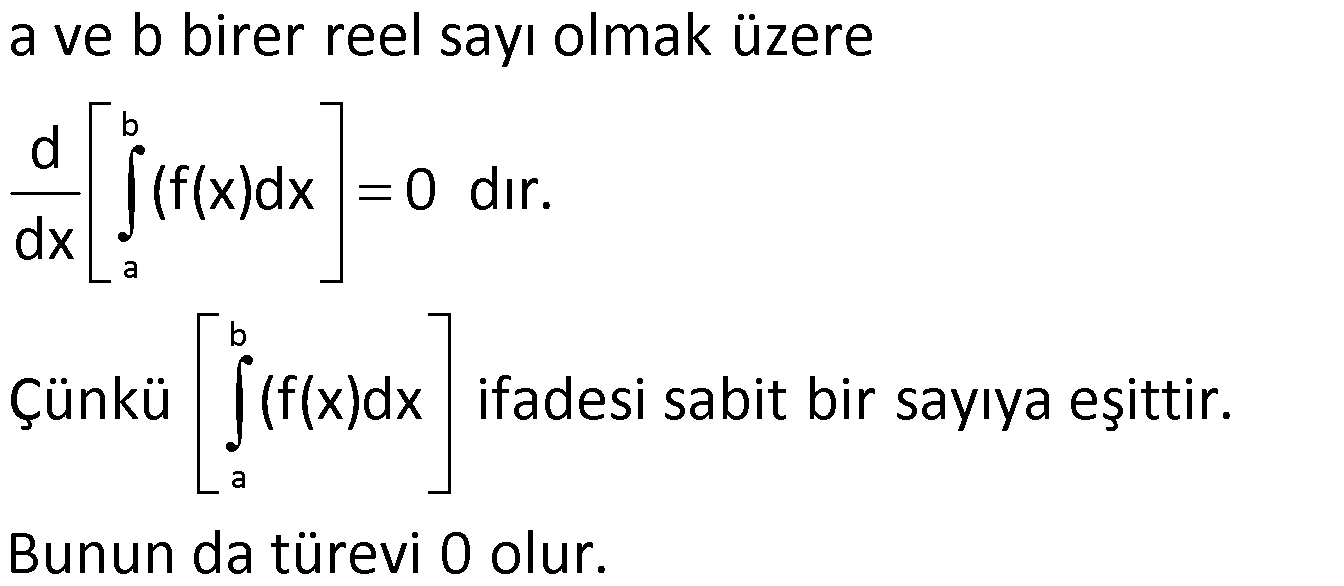
Not:
Örnek:
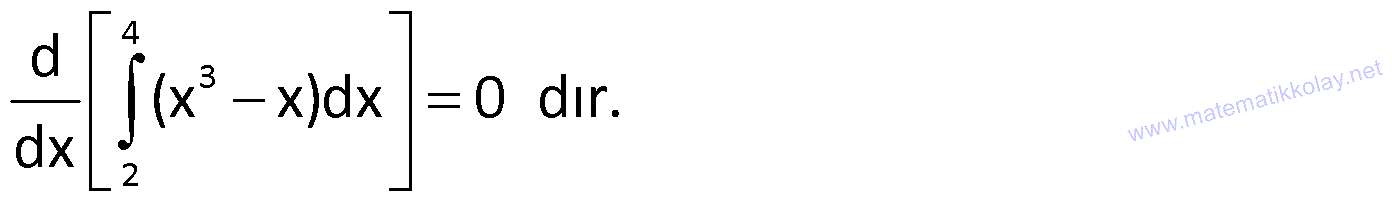
Not:
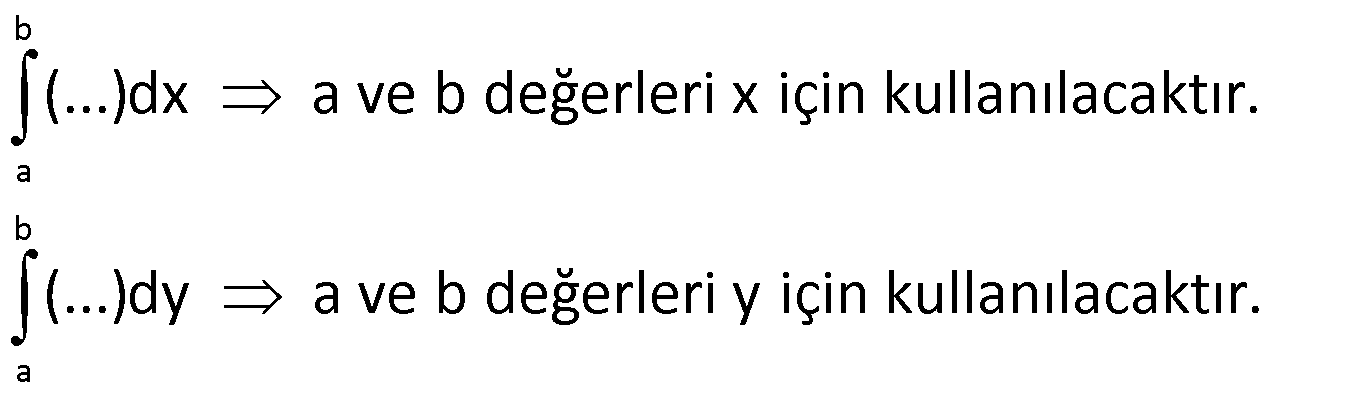
Örnek:

Çözüm:
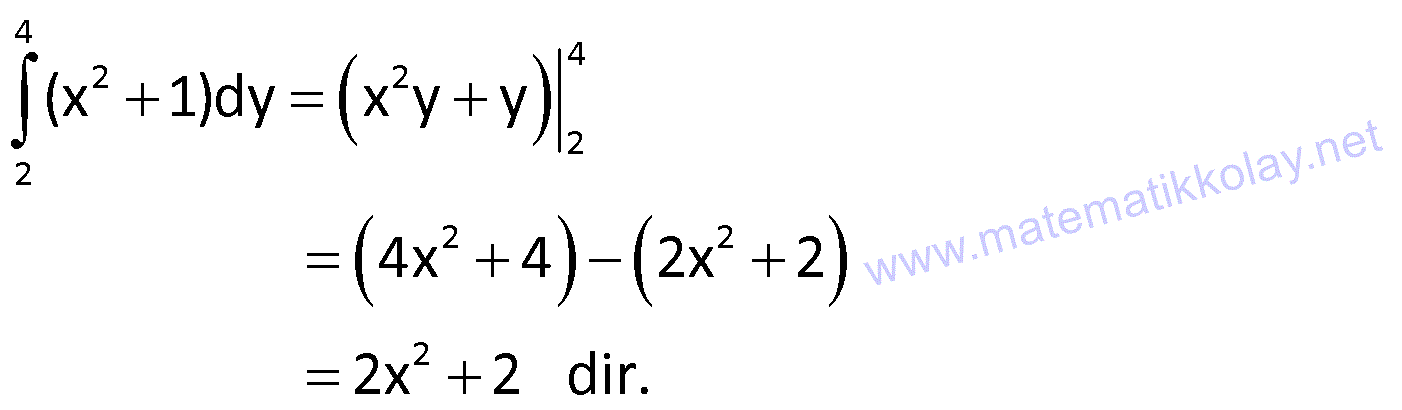
Not:

Örnek:
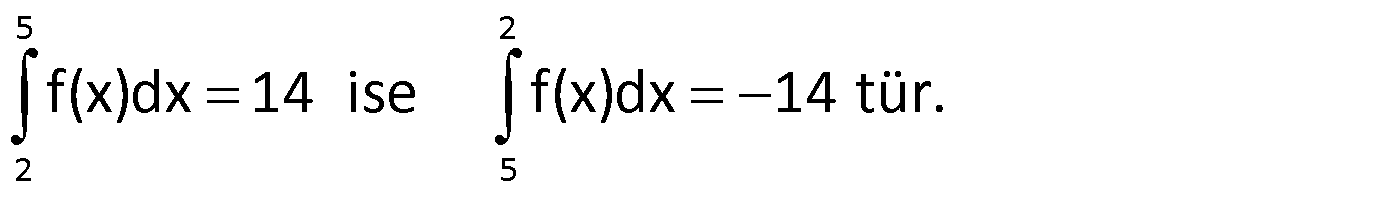
Not:

Örnek:
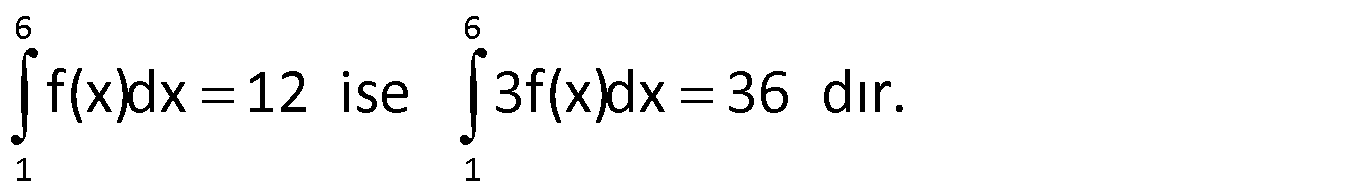
Not:

Örnek:

Not:
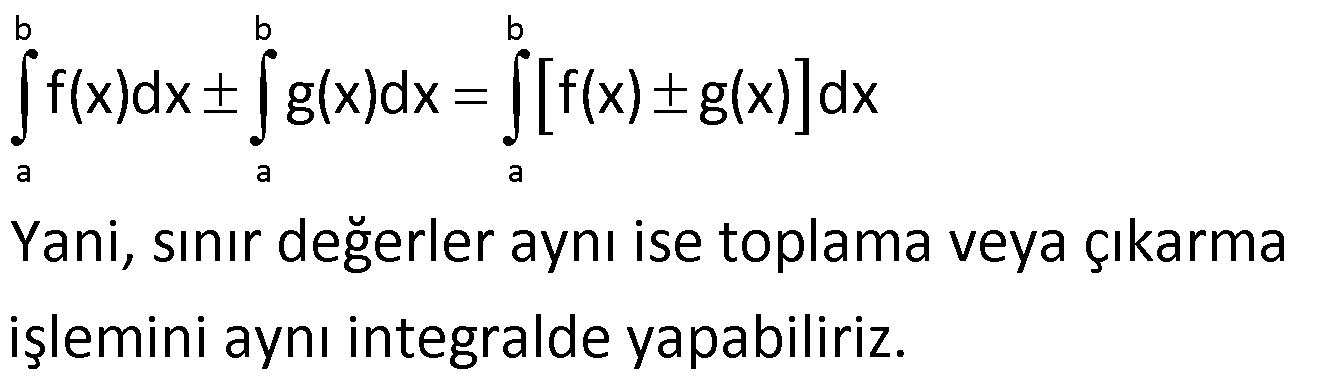
Örnek:
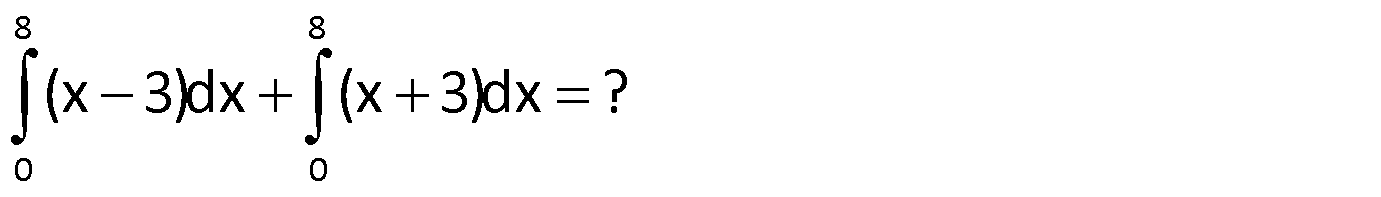
Çözüm:
Not:
Örnek:

Çözüm:
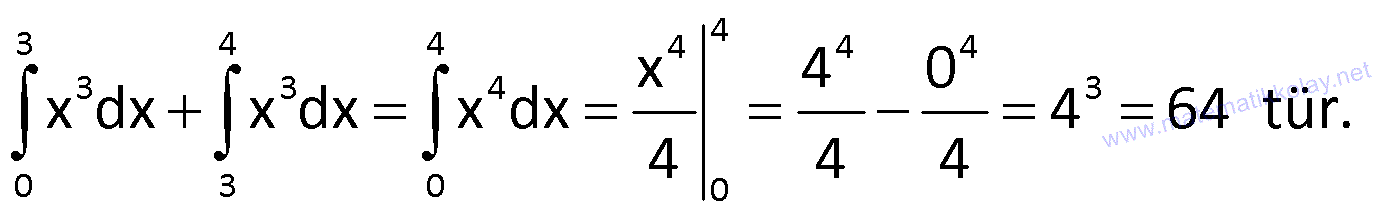
Not:

Örnek:

Not:

Örnek:

Çözüm:
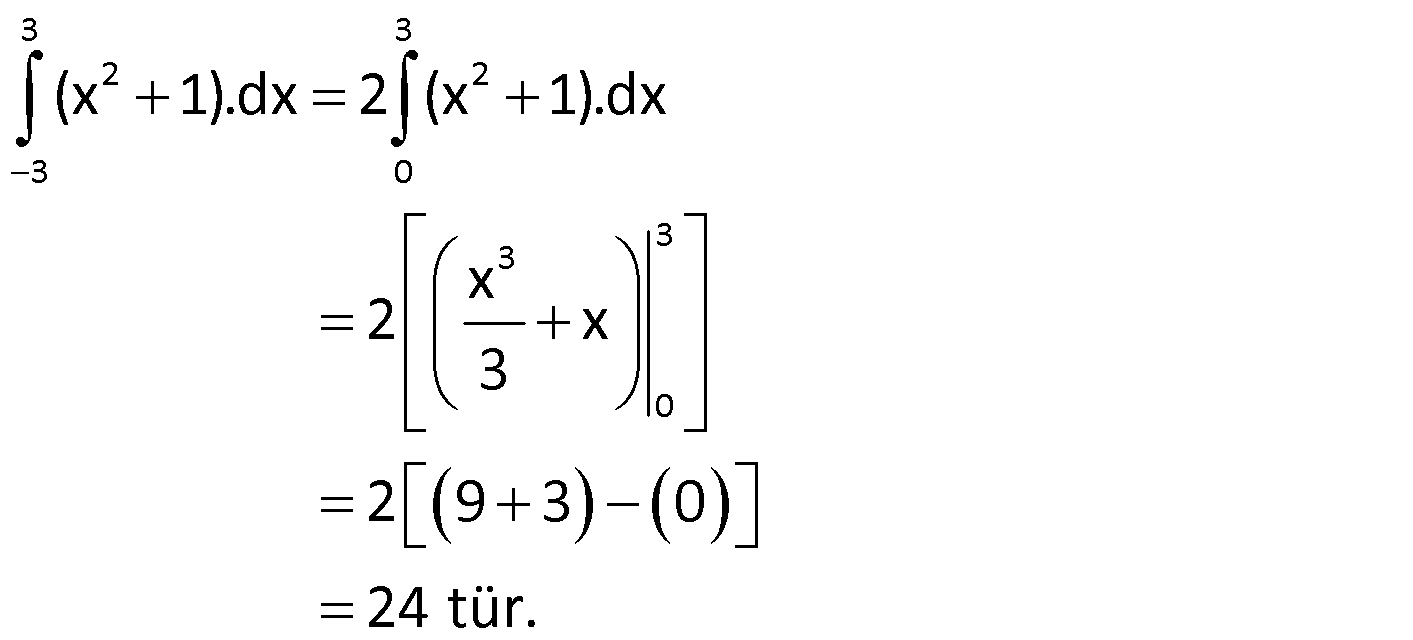
BELİRLİ İNTEGRALDE DEĞİŞKEN DEĞİŞTİRME

Örnek:

Çözüm:
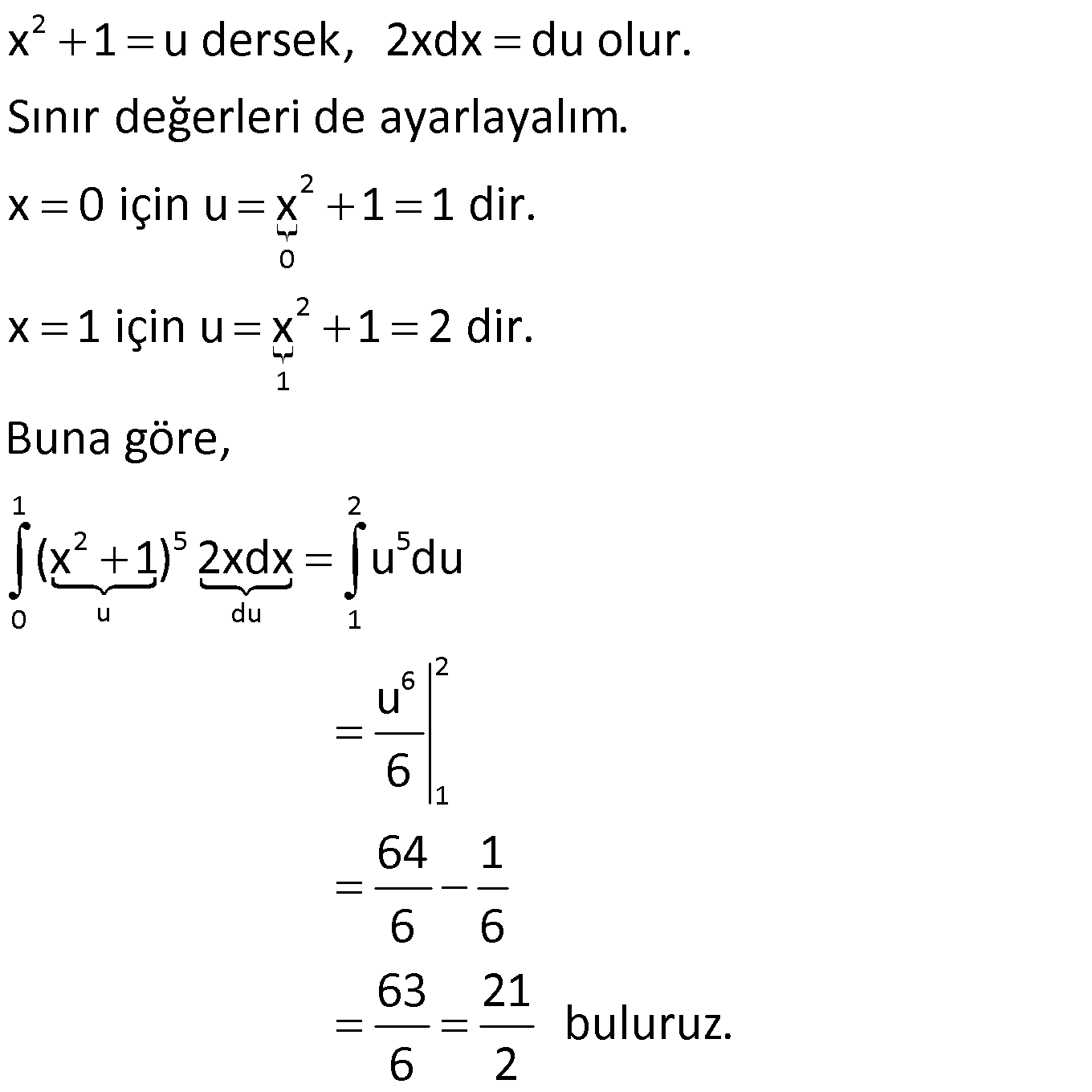
Belirli İntegralde Öteleme

Örnek:
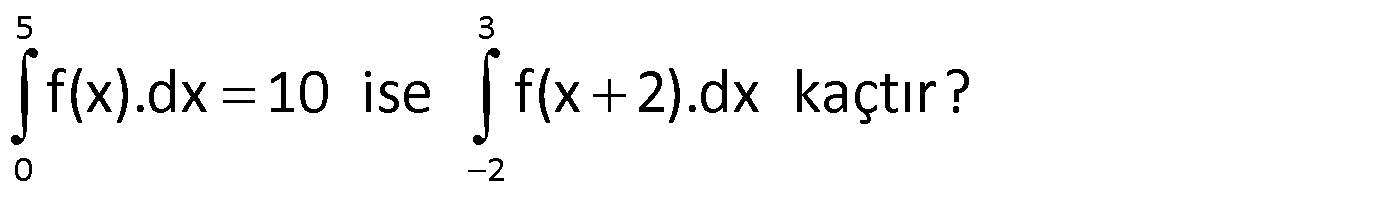
Çözüm:
Parçalı ve Mutlak Değerli Fonksiyonlarda İntegral

Örnek:

Çözüm:
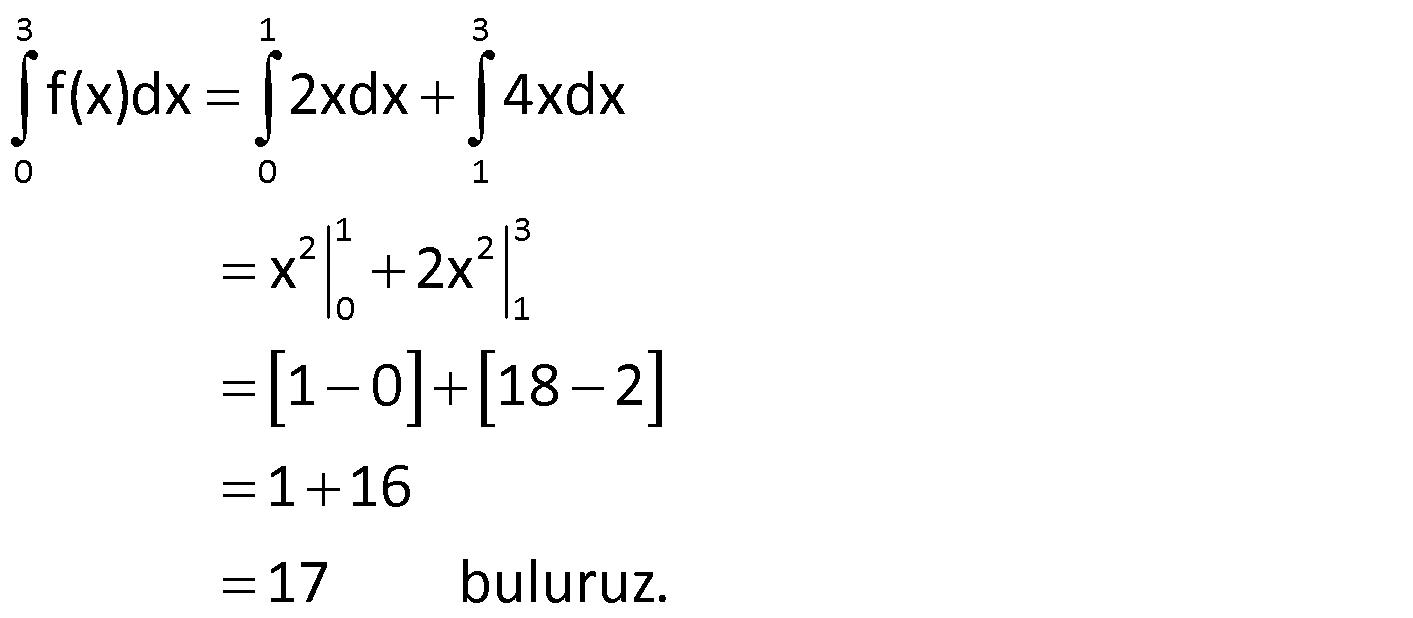
Not:

Örnek:

Çözüm:

3.sayfaya geçmek için Tıklayın.
(İntegral ile Alan)
| Konu ile ilgili Çözümlü Sorular veya Daha Fazlası için Tıkla |
| İntegral Konu Notlarını pdf indir |
| Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.) |
BELİRLİ İNTEGRAL VE ÖZELLİKLERİ b b a a f(x) fonksiyonu [a, b] aralığında türevlenebilir bir fonksiyon olsun. f'(x)dx f(x) f(b) f(a) dır. Bu integrale ise ” ” denir. (Çıkarma işleminde “c” integral sabiti Belirli İntegral kaybolur. ) Örnek: 6 2 (x 2)dx ? Çözüm: 6 6 2 2 2 x 36 4 (x 2)dx 2x 12 4 2 2 2 18 12 2 4 6 ( 2) 6 2 8 buluruz. Not: b a b a a ve b birer reel sayı olmak üzere d (f(x)dx 0 dır. dx Çünkü (f(x)dx ifadesi sabit bir sayıya eşittir. Bunun da türevi 0 olur. Örnek: 4 3 2 d (x x)dx 0 dır. dx Not: b a b a (…)dx a ve b değerleri x için kullanılacaktır. (…)dy a ve b değerleri y için kullanılacaktır. Örnek: 4 2 2 (x 1)dy ? Çözüm: 4 4 2 2 2 2 2 2 2 (x 1)dy x y y 4x 4 2x 2 2x 2 dir. Not: a b b a a ve b birer reel sayı olmak üzere, f(x)dx f(x)dx tir. Yani, sınır değerler yer değiştirirse sonuç, zıt işaretli olur. Örnek: 5 2 2 5 f(x)dx 14 ise f(x)dx 14 tür. Not: b b a a k bir reel sayı olmak üzere, k.f(x)dx k f(x)dx tir. Yani, katsayıyı integralin dışına alabiliriz. www.matematikkolay.net Örnek: 6 6 1 1 f(x)dx 12 ise 3f(x)dx 36 d ır. Not: a a f(x)dx 0 dır. Yani, sınır değerler aynı ise sonuç 0 dır. Örnek: 6 6 f(x)dx 0 d ır. Not: b b b a a a f(x)dx g(x)dx f(x) g(x) dx Yani, sınır değerler aynı ise toplama veya çıkarma işlemini aynı integralde yapabiliriz. Örnek: 8 8 0 0 (x 3)dx (x 3)dx ? Çözüm: (x 3 x 3 8 8 8 2 0 0 0 )dx 2xdx x 64 0 64 tür. Not: b c b a a c a c b olmak üzere, f(x)dx f(x)dx f(x)dx şeklinde iki integrale ayırabiliriz. Örnek: 3 4 3 3 0 3 x dx x dx ? Çözüm: 4 3 4 4 4 4 4 3 3 4 3 0 3 0 0 x 4 0 x dx x dx x dx 4 64 tür. 4 4 4 Not: a a f(x) tek fonksiyon ise f(x)dx 0 dır. Çünkü integral alınınca çift fonksiyon ortaya çıkar. Hem a için hem de a için aynı değeri verir. Bu sebeple aradaki fark 0 dır. Örnek: 500 3 500 (x x).dx 0 dır. Not: a a a 0 F(a) f(x) çift fonksiyon ise f(x)dx 2 f(x)dx tir. Çünkü integral alınınca tek fonksiyon ortaya çıkar. F(a) F( a) 2F(a) olur. Örnek: 3 2 3 (x 1).dx ? Çözüm: 3 3 2 2 3 0 3 3 0 (x 1).dx 2 (x 1).dx x 2 x 3 2 9 3 0 24 tür. BELİRLİ İNTEGRALDE DEĞİŞKEN DEĞİŞTİRME Belirli integralde değişken değiştirdikten sonra sınır değerleri de yeniden düzenlemeliyiz. Örnek: 1 2 5 0 (x 1) 2xdx ? Çözüm: www.matematikkolay.net 2 2 0 2 1 1 2 2 5 5 0 1 u du 2 6 1 x 1 u dersek, 2xdx du olur. Sınır değerleri de ayarlayalım. x 0 için u x 1 1 dir. x 1 için u x 1 2 dir. Buna göre, (x 1) 2xdx u du u 6 64 1 6 6 63 21 buluruz. 6 2 Belirli İntegralde Öteleme b k b k a k a k u x k u x k du dx du dx u a k k a u a k k a alt alt u b k k b u b k üst üst b f(u)du a Değişken değiştirerek de görebileceğimiz bu durumu kısaca şu şekilde ifade edebiliriz: f(x k)dx f(x k)dx b a k b b f(u)du a f(x)dx tir. Örnek: 5 3 0 2 f(x).dx 10 ise f(x 2).dx kaçtır? Çözüm: 2 3 3 5 2 0 u x 2 olsun. du dx olur. Sınır değerler, x 2 için u x 2 0 dır. x 3 için u x 2 5 tir. O halde, f(x 2).dx f(u).du 10 dur. Parçalı ve Mutlak Değerli Fonksiyonlarda İntegral Parçalı fonksiyonların belirli integralini alırken kritik değerlere göre integrali parçalayıp, sonra integral almalıyız. Örnek: 3 0 2x , x 1 f(x) olduğuna göre, 4x , x 1 f(x)dx integralinin değeri kaçtır? Çözüm: 3 1 3 0 0 1 1 3 2 2 0 1 f(x)dx 2xdx 4xdx x 2x 1 0 18 2 1 16 17 buluruz. Not: Mutlak değer fonksiyonlarının belirli integralini alırken de kritik noktalara göre fonksiyonu parçalayıp sonra integral almalıyız. Örnek: 2 0 2x 2 dx ? Çözüm: www.matematikkolay.net 2 0 1 2 0 1 mutlak mutlak değerin değerin içi içi 1 2 0 1 1 2 2 2 0 1 2x 2 dx x 1 den önce ve sonrası şeklinde ayırmalıyız. 2x 2dx 2x 2dx ( 2x 2)dx (2x 2)dx x 2x x 2x 1 2 0 4 4 1 2 1 0 ( 1) 1 1 2 dir.

