 Bu bölümde Üçgende Kenarortay ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Üçgende Kenarortay ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
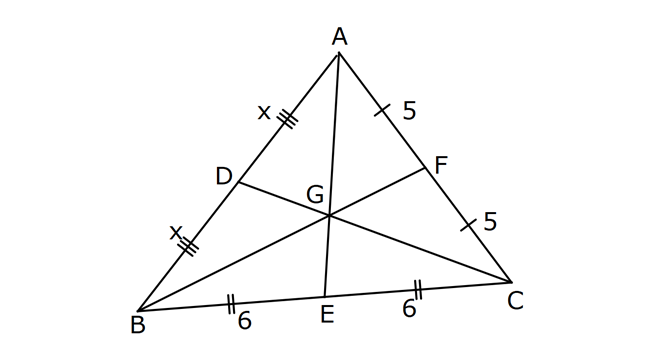
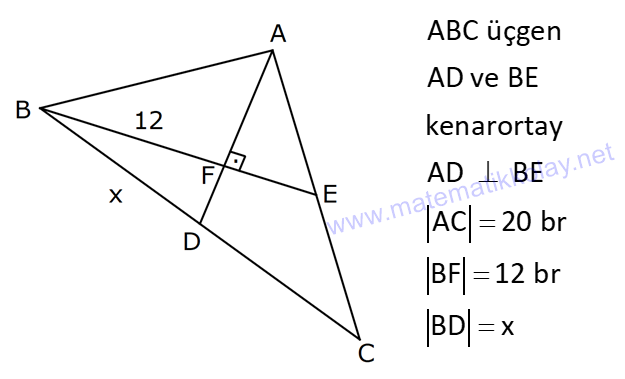
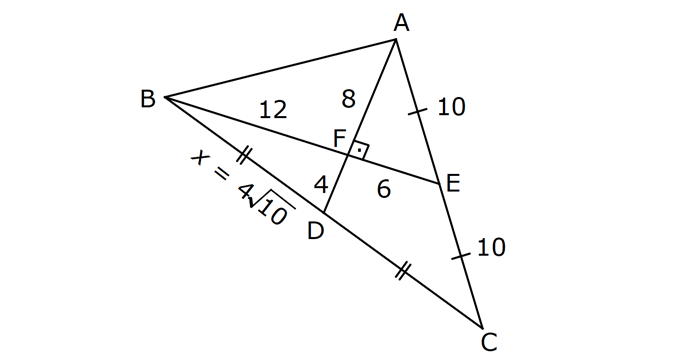
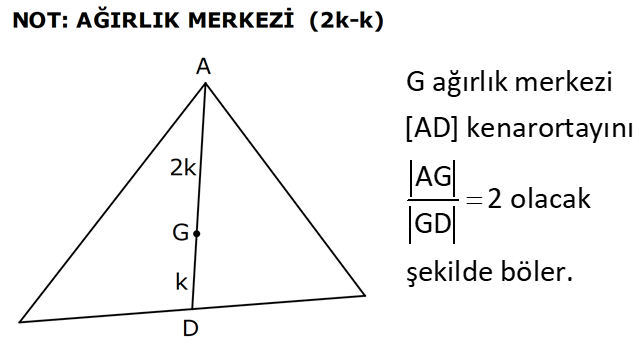
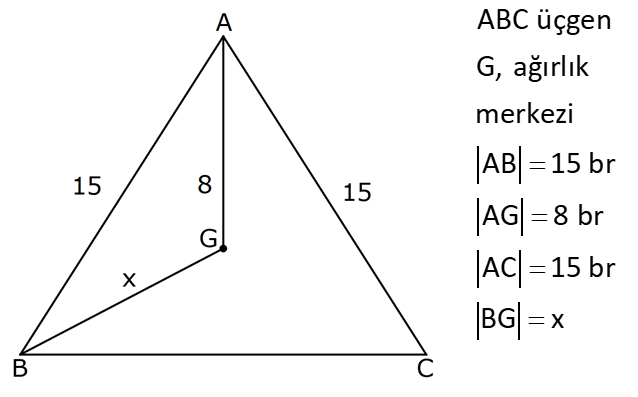
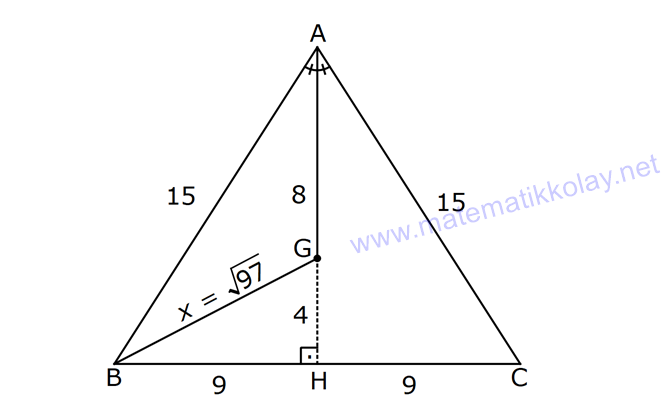
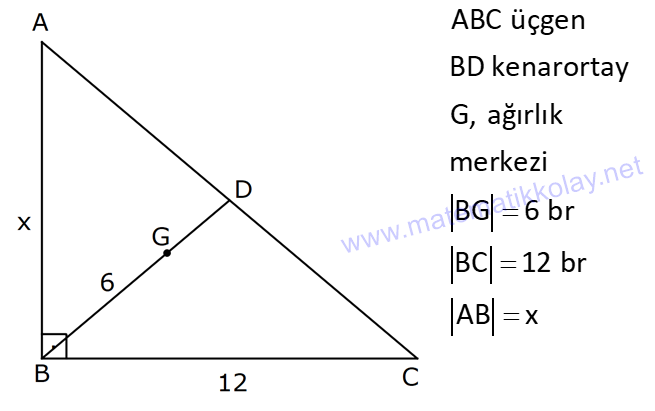
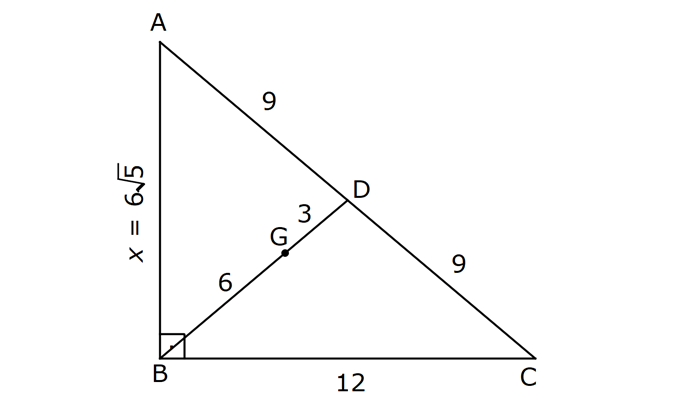
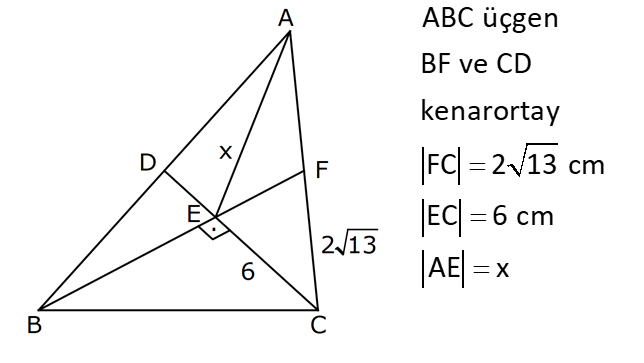
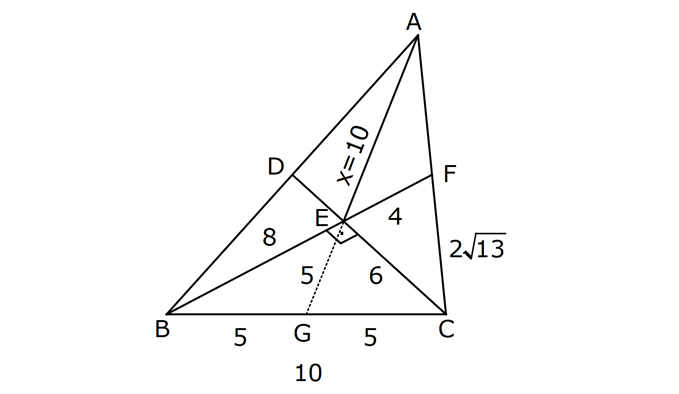
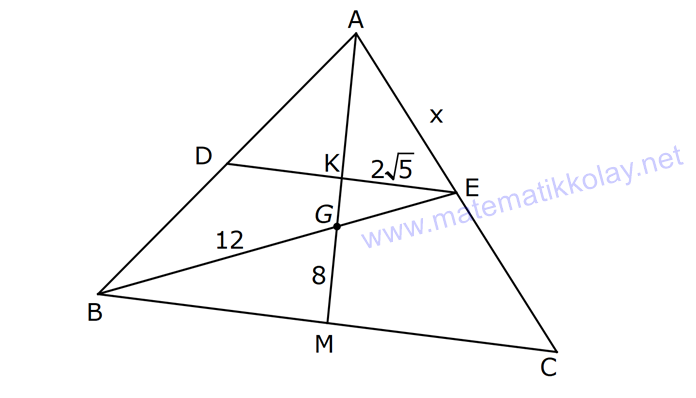
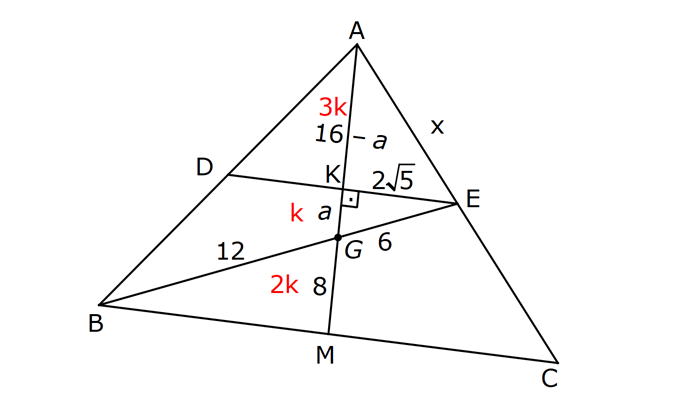
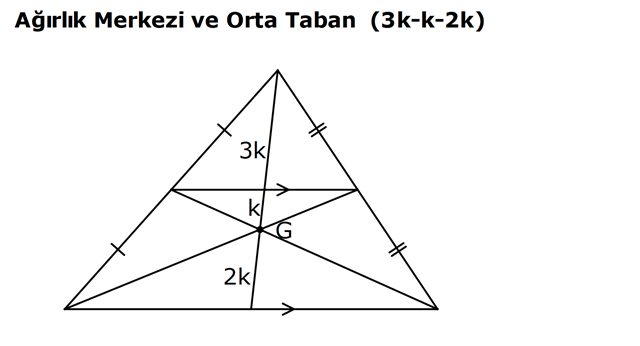
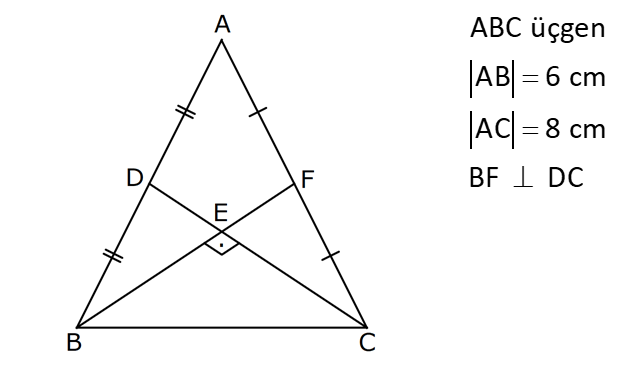
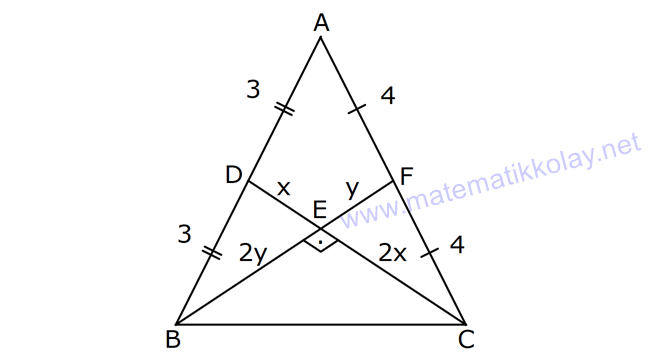
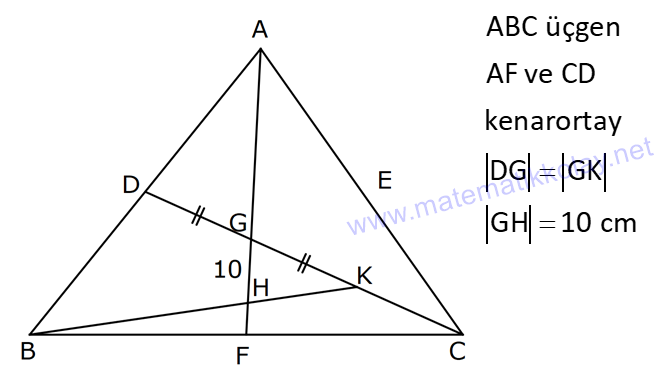
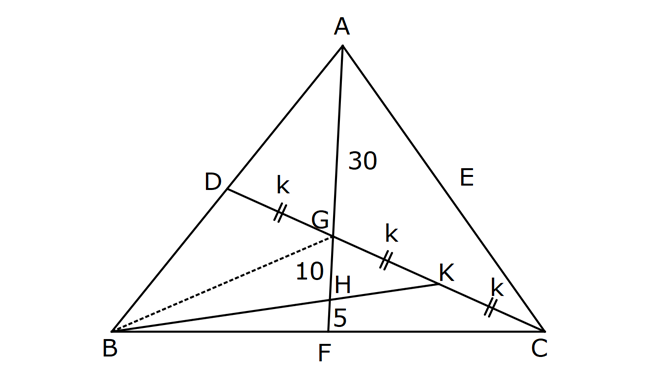
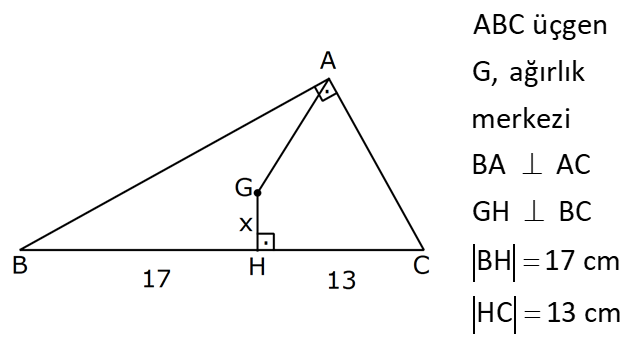
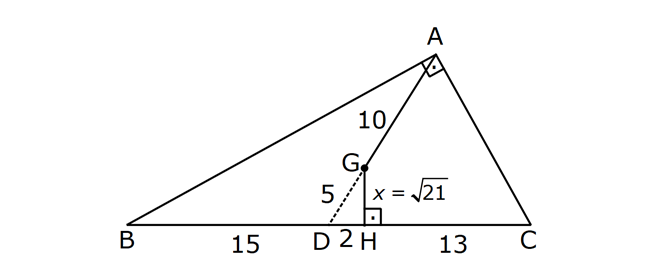
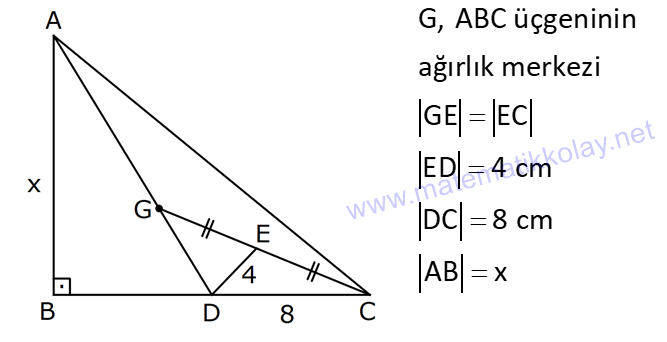
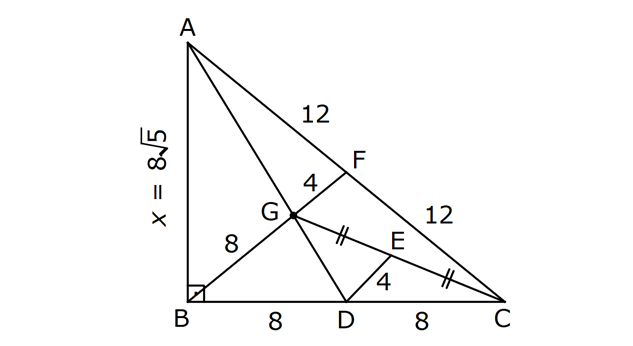
ÜÇGENDE KENARORTAY www.matematikkolay.net 1) ABC üçgen, G, ağırlık merkezi BE 6 cm AF 5 cm Ç(ABC) 30 cm BD x [AE], [CD], [BF] doğru parçaları G noktasında kesiştiklerine göre, x kaç cm dir? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: Bir üçgende kenarortaylar bir noktada kesişir. Bu noktaya da denir. Dolayısıyla [AE], [CD] ve [BF] birer kenarortaydır. Bulundukları kenarı iki eş parçaya ayırmıştır. Bu sebeple, üçgenin ağırlık merkezi AC BC AB FC 5 cm, EC 6 cm, AD x cm dir. Üçgenin çevresi 30 cm ise, 30 5 5 6 6 x x 30 22 2x 8 2x x 4 cm dir. Cevap : C 2) ABC üçgen AD ve BE kenarortay AD BE AC 20 br BF 12 br BD x Yukarıda verilenlere göre x kaç br dir? A) 4 B) 3 5 C) 6 D) 4 10 E) 8 ÇÖZÜM: 20 BE kenarortay olduğundan, AE 10 br dir. 2 F noktası ağırlık merkezidir. Çünkü iki kenarortay burada kesişmiş. Ağırlık merkezi, kenarortayı köşeden kenara doğru 2’ye 1 oranında ayırır. 12 Bu nedenle FE 6 2 2 2 2 2 2 br dir. O halde AFE üçgeni bir 6 – 8 -10 üçgenidir. AF 8 br olur. Yine ağırlık merkezinden dolayı AF ile FD arasında 2 ye 1 oran vardır. 8 FD 4 br dir. 2 BFD üçgeninde pisagor yaparsak, x 12 4 x 144 16 x 160 x 160 x 16.10 4 10 br dir. Cevap : D www.matematikkolay.net G ağırlık merkezi [AD] kenarortayını AG 2 olacak GD şekilde böler. 3) ABC üçgen G, ağırlık merkezi AB 15 br AG 8 br AC 15 br BG x Yukarıda verilenlere göre, x kaç br dir? A) 73 B) 78 C) 82 D) 85 E) 97 ÇÖZÜM: İkizkenar üçgende tepe açıdan inen kenarortay, hem yükseklik hem de açıortaydır. 8 G ağırlık merkezi olduğundan GH 4 br olur. 2 AH 12 br olur. AHB üçgeni 9 -12 -15 üçgenidir (3k – 4k – 5k). BH 9 br olur. BHG üç 2 2 2 geninde pisagor yaparsak, x 4 9 16 81 97 x 97 br olur. Cevap : E 4) ABC üçgen BD kenarortay G, ağırlık merkezi BG 6 br BC 12 br AB x Yukarıda verilenlere göre, x kaç br dir? A) 6 5 B) 10 C) 8 6 D) 12 E) 10 3 ÇÖZÜM: www.matematikkolay.net Ağırlık merkezi, kenarortayı köşeden kenara 2’ye 1 6 oranında ayırır. Bu sebeple GD 3 br dir. 2 Ayrıca, dik açıdan inen kenarortay oluşturur. Yani, AD DC BD 9 br dir. Bu sebeple AC 18 br ol muhteşem üçlüyü 2 2 2 2 2 ur. ABC üçgeninde pisagor yaparsak, x 12 18 x 144 324 x 180 x 180 36.5 6 5 br dir. Cevap : A 5) ABC üçgen BF ve CD kenarortay FC 2 13 cm EC 6 cm AE x Yukarıda verilenlere göre, x kaç cm dir? A) 8 B) 10 C) 12 D) 13 E) 14 ÇÖZÜM: 2 2 2 2 2 EFC üçgeninde pisagor yaparsak, EF 6 2 13 EF 36 52 EF 16 EF 4 cm olur. Kenarortayların kesişim noktası olduğundan F nok – tası ağırlık merkezidir. BE 2.4 8 cm olur. EBC üçgeni 6 – 8 -10 üçgenidir. BC 10 cm olur. AE uzunluğunu uzatarak, kenarortayı çizelim. E açısı dik açı olduğundan, muhteşem üçlü oluşur. BG GC EG 5 cm olur. AE uzunluğu da EG ‘nin 2 katı olduğundan, AE 10 cm olur. Cevap : B 6) ABC üçgen, G ağırlık merkezi, DE // BC B,G,E doğrusal ve A,K,G,M doğrusal BG 12 cm, GM 8 cm ve KE 2 5 cm olduğuna göre, AE x kaç cm dir? A) 3 17 B) 2 41 C) 4 19 D) 103 E) 152 ÇÖZÜM: www.matematikkolay.net 12 G ağırlık merkezi olduğundan GE 6 cm dir. 2 E noktası, AC kenarının orta noktasıdır. DE // BC olduğundan, DE orta tabandır. Bu şekilde olunca kenarortay, köşeden kenara 3-1-2 oranında bölünür. 2k 8 olduğundan, KG k 4 tür. AG 8.2 16 cm dir. KG a diyelim. AK 16 a cm olur. DE orta taban olduğu için AK KM olmalıdır. 16 a 8 a KG ‘yi bulmak için 2.Yol: 2 2 2 2 2 2 8 2a a 4 cm dir. KGE üçgeni bir dik üçgen çıkar. Çünkü 4 2 5 6 eşitliğini sağlar. K açısı 90 ise, AKE üçgeninde de pisagor yapabiliriz. AK 3k 12 cm dir. x 12 2 5 144 20 164 x 164 4.41 2 41 cm buluruz. Cevap : B 7) ABC üçgen AB 6 cm AC 8 cm BF DC Yukarıda verilenlere göre BC kaç cm dir? A) 4 B) 3 2 C) 2 5 D) 5 E) 6 ÇÖZÜM: 2 2 2 2 2 2 İki kenarortayın kesiştiği E noktası, üçgenin ağırlık merkezidir. DE x dersek, EC 2x olur. EF y dersek, BE 2y olur. BED üçgeninde pisagordan, x (2y) 3 x 4y 9 olur. FEC üçgeninde pisagordan, y ( 2 2 2 2 2 2 2 2 2 2 2 2 2 5 2x) 4 y 4x 16 olur. Taraf tarafa toplarsak, 5x 5y 25 olur. Her tarafı 5’e bölelim. x y 5 olur. EBC üçgeninde pisagordan, BC 4x 4y dir. 4(x y ) 20 dir. BC 20 2 5 cm dir. Ceva p : C www.matematikkolay.net 8) ABC üçgen AF ve CD kenarortay DG GK GH 10 cm Yukarıda verilenlere göre, AG kaç cm dir? A) 20 B) 24 C) 25 D) 30 E) 40 ÇÖZÜM: DG k dersek, GC 2k olur. GK k olduğundan, KC k kalır. O halde, BGC üçgeni için BK bir kenarortaydır. GF doğrusu zaten bir kenarortaydı. Buna göre, H noktası, BGC üçgeninin ağırlık merkezidir. HF 10 5 cm olur. GF 15 cm olur. 2 AG 2.15 30 cm olur. Cevap: D 9) ABC üçgen G, ağırlık merkezi BA AC GH BC BH 17 cm HC 13 cm Yukarıda verilenlere göre, GH x kaç cm dir ? A) 3 B) 14 C) 4 D) 3 2 E) 21 ÇÖZÜM: AG yi uzatarak, kenarortayı çizelim. BC 30 cm olduğundan, 15 cm olarak iki eş parçaya ayrılır. DH 2 cm kalır. A açısı 90 olduğundan muhteşem üçlü oluşur. AD 15 cm olur. Ağırlık merkezi 10 ve 5 cm olarak 2 2 2 2 2 ayırır. GD 5 cm olur. GHD üçgeninde pisagor yaparsak, x 2 5 x 4 25 x 21 x 21 cm olur. Cevap : E 10) G, ABC üçgeninin ağırlık merkezi GE EC ED 4 cm DC 8 cm AB x Yukarıda verilenlere göre, x kaç cm dir? A) 16 B) 10 3 C) 8 5 D) 24 E) 6 10 ÇÖZÜM: www.matematikkolay.net BF kenarortayını çizelim. [ED], BGC üçgeninde bir orta tabandır. Çünkü E ve D, bulundukları kenarın tam orta noktasıdır. Bu sebeple BG 2.4 8 cm olur. 8 G ağırlık merkezi olduğundan GF 4 cm olur. 2 B açısı 9 2 2 2 2 2 0 olduğundan muhteşem üçlü oluşur. AF FC BF 12 cm olur. ABC üçgeninde pisagor yaparsak, x 16 24 x 256 576 x 320 x 320 64.5 8 5 cm buluruz. Cevap : C
 Bu bölümde Üçgende Kenarortay ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Üçgende Kenarortay ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar… 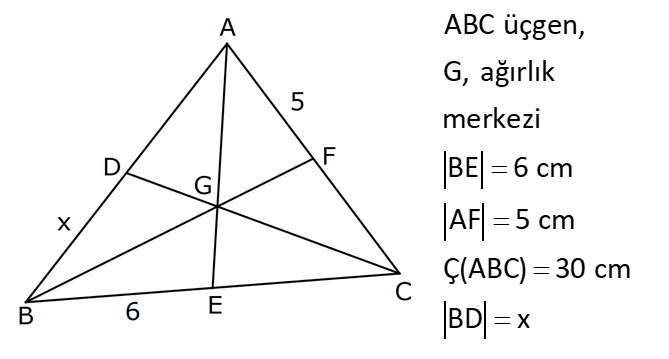
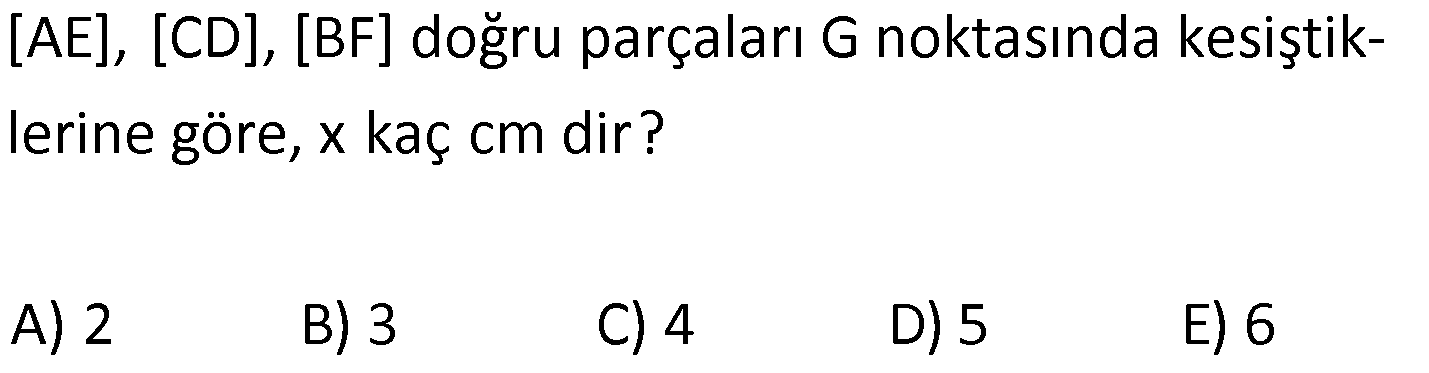

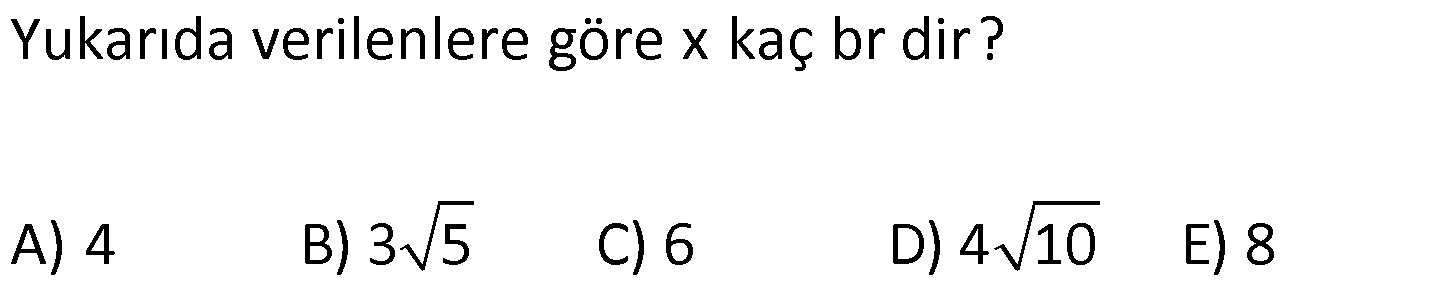

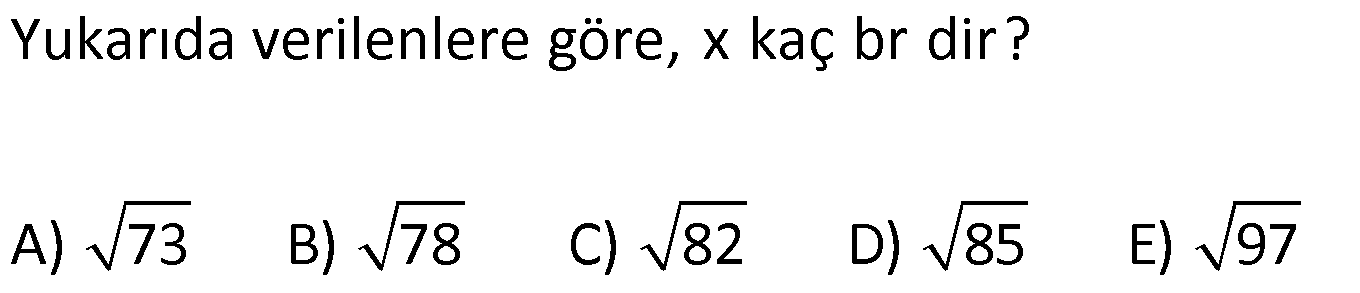




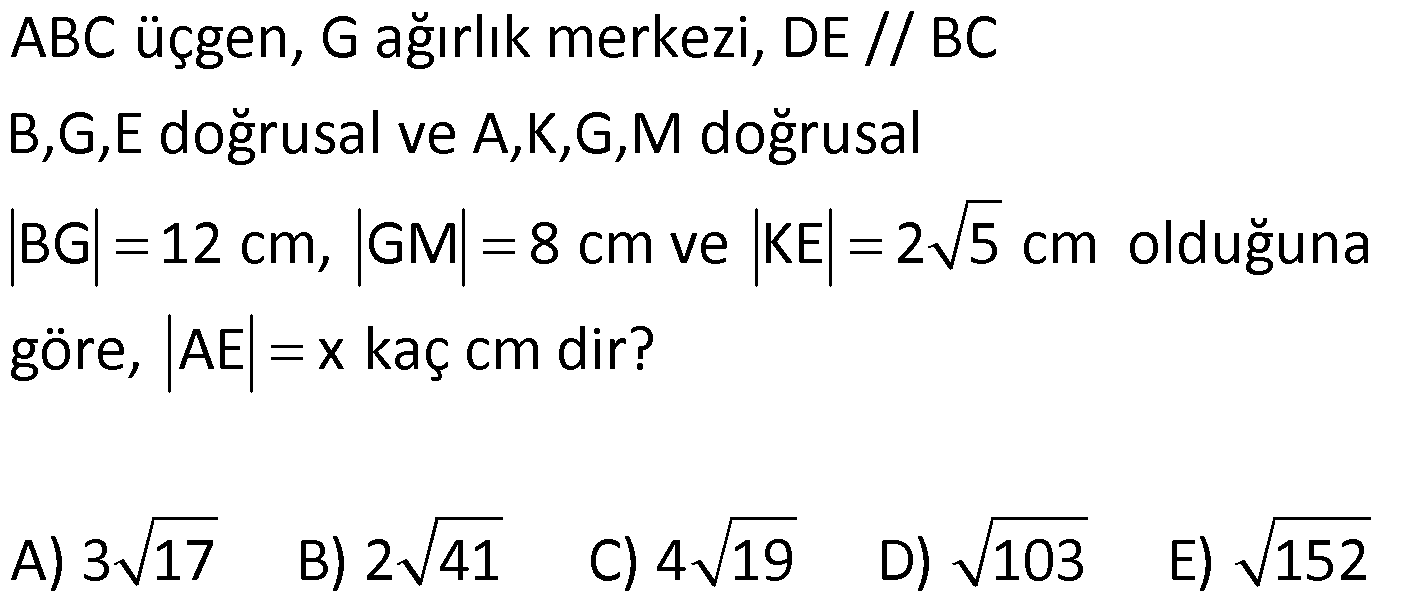

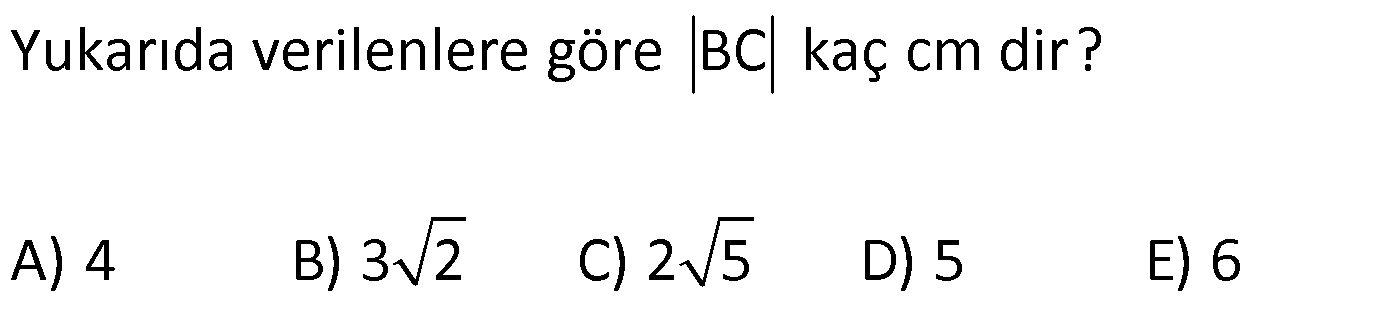

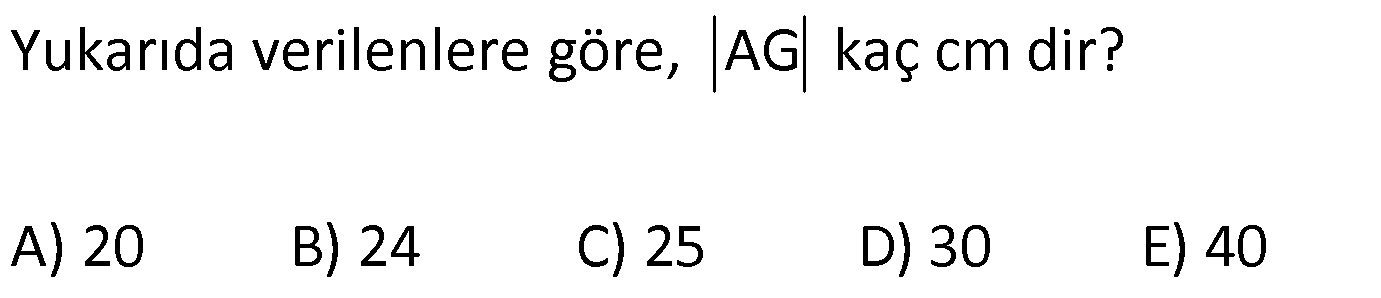

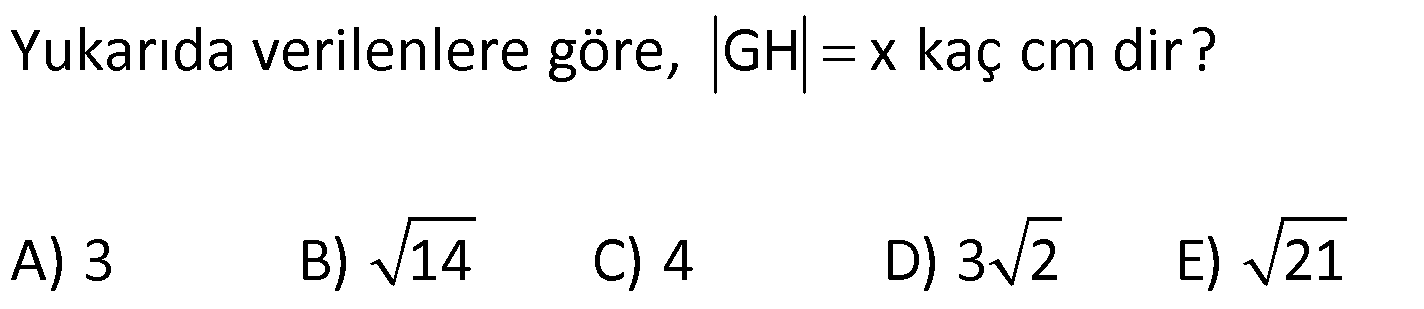

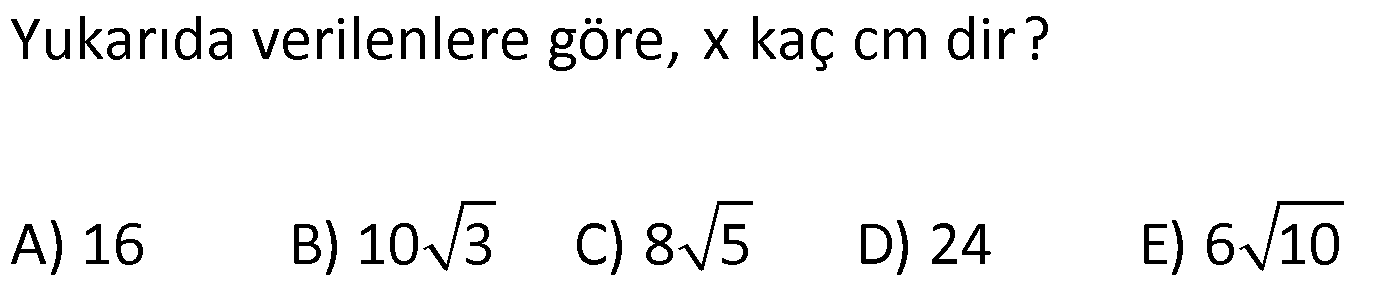



Sevdiğine söyleyecek bir şey bulamadığında limon at derler… 🍋