 Bu bölümde İşçi Problemleri ile ilgili 15 adet soru bulunmaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…
Bu bölümde İşçi Problemleri ile ilgili 15 adet soru bulunmaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…
SORULAR
SORU 1
Mehmet, bir işi tek başına 15 saatte; Rıza ise 30 günde bitirebilmektedir. Buna göre, ikisi birlikte aynı işi kaç günde bitirebilir?
A) 8 B) 10 C) 11 D) 12 E) 13
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 2
Necati bir işi tek başına 24 günde, Hasan ise 8 günde yapabilmektedir. Necati ve Hasan’ın arkadaşı olan Recep’in katılımıyla üçü beraber bu işi 4 günde bitirebiliyorlar. Buna göre Recep, bu işi tek başına kaç günde bitirir?
A) 6 B) 8 C) 10 D) 12 E) 15
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 3
Sefa bir işin ini 6 günde, Ata aynı işin yarısını 3 günde yapabiliyor. Sefa, Ata ve Arda üçü birlikte bu işi 3 günde bitirebildiğine göre, Arda tek başına bu işin
ünü kaç günde bitirebilir?
A) 5 B) 8 C) 10 D) 12 E) 15
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 4
Türkan bir işin ünü 8 saatte, Necla ise aynı işin yarısını 8 saatte bitiriyor. İkisi beraber 3 saat çalışırlarsa bu işin ne kadarını bitirirler?
![]()
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 5
Merve bir işi tek başına 12 saatte, Özlem ise 18 saatte bitirebiliyor. Merve 3 saat, Özlem 6 saat çalıştığında işin kaçta kaçı bitir?
![]()
| Doğru Cevap | Çözüm için Tıklayınız |
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
SORU 6
Azra bir işi 12 günde, Ayten 60 günde yapabiliyor. Buna göre, Azra ile Ayten birlikte bu işin ini kaç günde bitirirler?
A) 3 B) 4 C) 5 D) 6 E) 7
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 7
Bir işi tek başına Hatice 80 günde, Zeynep 120 günde bitirebiliyor. İkisi birlikte çalışarak işi tamamladığında Hatice işin kaçta kaçını yapmıştır?
![]()
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 8
Kerim bir işi tek başına 12 saatte, Fatih ise aynı işi 8 saatte bitirebiliyor. İkisi beraber işe başladık tan 2 saat sonra Kerim işten ayrılıyor. Geriye kalan işi Fatih kaç saatte bitirir?
![]()
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 9
Tevfik bir işi tek başına 15 günde, Derya 20 günde, Mert ise 24 günde bitirebilmektedir. Üçü beraber 4 gün çalıştıktan sonra, Tevfik rahatsızlanıyor
ve işi bırakıyor. Kalan işi diğerleri kaç günde tamamlar?
A) 1 B) 2 C) 3 D) 4 E) 5
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 10
Furkan ve Hasan bir işi birlikte 15 günde tamamlayabiliyorlar. İkisi birlikte 5 gün çalıştıktan sonra Hasan işi bırakıyor ve geri kalan işi Furkan 20 günde bitiriyor. Buna göre Hasan bu işi tek başına bu işi kaç günde bitirir?
A) 25 B) 30 C) 32 D) 35 E) 40
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 11
Özcan’ın çalışma hızı, Ender’in çalışma hızının iki katıdır. İkisi beraber bir işi 15 günde bitirebiliyorlar. Eğer Ender çalışma hızını 3 katına çıkarırsa bu işi kaç günde bitirebilirler?
A) 6 B) 7 C) 8 D) 9 E) 10
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 12
Bir işi 4 usta 5 günde, 8 çırak 10 günde yapabiliyor. Buna göre bu işi, 1 usta ve 1 çırak kaç günde bitirir?
A) 12 B) 14 C) 16 D) 18 E) 20
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 13
Bir terzi 3 günde 1 elbise, kalfası ise 9 günde 2 elbise dikebilmektedir. Buna göre, terzi ile kalfası 75 tane elbiseyi kaç günde bitirebilir?
A) 90 B) 105 C) 120 D) 125 E) 135
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 14
Şevket ile Hikmet beraber bir işi 12 günde, Şevket ile Necdet 16 günde, Hikmet ile Cevdet ise 8 günde bitirebiliyor. Buna göre, Melih bu işi tek başına kaç günde bitirir?
A) 64 B) 96 C) 72 D) 56 E) 48
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 15
Aynı nitelikteki 12 işçi bir işi 10 saatte bitiriyor. İşe başladıktan 3 saat sora 5 işçi işi bırakıyor. Buna göre, kalan işi diğer işçiler kaç saatte bitirir?
A) 9 B) 10 C) 11 D) 12 E) 13
| Doğru Cevap | Çözüm için Tıklayınız |
SORU ÇÖZÜMLERİ
ÇÖZÜM 15
Bir işçinin bir saatteki iş yapma hızına V dersek,
12 işçi 10 saatte : 12.10.V =120V lik bir iş yapar.
12 işçi 3 saat çalışınca : 12.3.V=36V lik iş biter.
Geriye 120V – 36V = 84V lik iş kalır.
5 işçi ayrılınca geriye kalan 7 işçi, 84V lik işi
![]()
saatte tamamlar.
Doğru Cevap : D şıkkı
| Soruyu Gör |
ÇÖZÜM 14
Şevket, Hikmet ve Necdet bu işi tek başlarına sırasıyla x,y ve z günde bitirebilsin.
Buna göre;
![]()
![]()
![]()
![]()
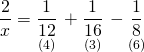
![]()
![]()
![]()
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 13
Terzinin 1 günde dikebileceği elbise:
Kalfanın 1 günde dikebileceği elbise: dur.
İkisi beraber 75 elbiseyi;
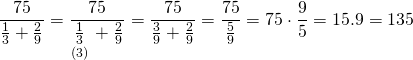
135 günde dikebilir.
Doğru Cevap : E şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 12
4 usta bir işi 5 günde yapabiliyorsa,
bir usta bu işi 20 günde bitirir.
8 çırak bu işi 10 günde tamamlayabiliyorsa
bir çırak bu işi 80 günde yapabilir.
Bir usta ve bir çırak bu işi x günde bitirebiliyorsa;
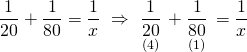
![]()
x = 16 gün bulunur.
Doğru Cevap : C şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 11
Ender’in Çalışma Hızı: V
Özcan’ın Çalışma Hızı: 2V
İkisinin toplam hızı 3V’dir.
15 günde yapılan iş 3V.15 45V lik bir iştir.
Ender’in çalışma hızı 3V olunca,
Toplam Hız = 2V + 3V = 5V olur.
45V lik bir iş günde biter.
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 10
Furkan ve Hasan bu işi beraber 15 günde bitirebiliyordu. Bu ikisi 5 gün çalıştıysa bu işin ini bitirmişlerdir. Geriye bu işin
i kalmıştır.
Furkan, bu işi tek başına x günde bitirebiliyorsa;
![]()
![]()
![]()
x=30 gün bulunur.
Hasan, bu işi tek başına y günde bitirebiliyorsa;
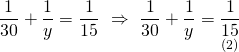
![]()
![]()
y = 30 gün buluruz.
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 9
Tevfik 1 günde işin ini,
Derya 1 günde işin sini,
Mert 1 günde işin ünü yapabilir.
Tevfik ayrıldıktan sonra işi bitirmek için geçen gün sayısına x diyelim ve denklemi oluşturalım.
![]()
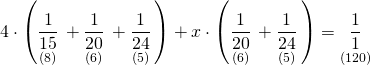
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 8
Kerim’in 1 saatte yaptığı iş dir.
Fatih’in 1 saatte yaptığı iş dir.
Fatih’in kalan kısmı x saatte bitirmiş olsun,
Buna göre denklem kuralım.
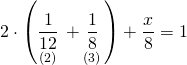
saatte bitirir.
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 7
İkisi beraber bu işi kaç günde bitirir, onu bulalım.
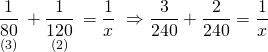
![]()
x = 48 gün buluruz.
48 günde Hatice bu işin kadarını yapmıştır.
buluruz.
2.Yol:
Hatice bu işi 80 günde, Zeynep 120 günde yapıyorsa
Hatice’nin iş yapma hızına 3V dersek.
Zeynep’in iş yapma hızı 2V olur.
İkisi beraber 5V hızında çalışır.
Hatice’nin yaptığı iş: buluruz.
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 6
Azra 1 günde işin sini,
Ayten ise 1 günde işin ını yapıyor.
Buna göre denklemi kuralım,
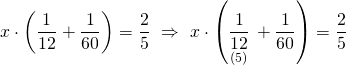
![]()
![]()
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 5
Merve 1 saatte bu işin sini,
Özlem de 1 saatte bu işin ini bitirir.
Buna göre;
Merve 3 saat, Özlem 6 saat çalıştığında
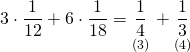
![]()
Bu işin si bitmiş olur.
Doğru Cevap :C şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 4
Türkan bu işin ünü 8 saatte bitiriyorsa, tamamını 4.8=32 saatte bitirir.
Necla ise bu işin tamamını 16 saatte bitirir.
Türkan 1 saatte bu işin sini,
Necla da 1 saatte bu işin sını bitirebiliyor.
İkisi beraber 3 saatte;
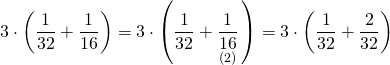
![]()
sini bitirirler.
Doğru Cevap : E şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 3
İlk önce kişilerin, bu işin tamamını, tek başına kaç günde yapabileceklerini bulalım,
Sefa bu işin ini 6 günde yapabiliyorsa, tamamını
günde yapar.
Ata bu işin yarısını 3 günde yapabiliyorsa, tamamını 3.2 = 6 günde yapar.
Arda bu işi x günde bitiriyor diyelim. Buna göre;
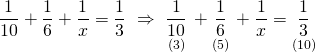
![]()
![]()
x=15 buluruz.
Arda bu işi 15 günde bitirebiliyorsa ünü 5 günde bitirebilir.
Doğru Cevap : A şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 2
Recep, bu işi tek başına x günde bitiriyor diyelim,
Buna göre denklemi oluşturalım.
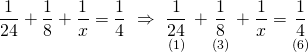
![]()
![]()
![]()
![]()
![]()
![]()
Recep bu işi tek başına 12 günde bitirebilir.
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 1
İşçi problemlerinde formülden yararlanarak çözmeye çalışalım.
İkisi beraber t günde bitirebilir dersek,
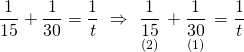
![]()
İkisi beraber 10 günde bu işi bitirebilir.
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |


Sevket sorusunda necdet is yapmiyor sanirim..hatali.
Uyarınız için teşekkürler. Hata düzeltildi. Artık herkes çalışıyor 🙂