 Bu bölümde Mutlak Değer ile ilgili 22 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Mutlak Değer ile ilgili 22 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…










Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
MUTLAK DEĞER ÇÖZÜMLÜ SORULAR www.matematikkolay.net 1) |6 2| |2 5| |1 4| işleminin sonucu kaçtır? A) 2 B) 2 C) 5 D) 7 E) 12 ÇÖZÜM: 4 3 5 İlk önce mutlak değerlerin içindeki işlemleri yapalım. |6 2| |2 5| |1 4| |4| | 3| |5| Mutlak değerin içindeki değer, dışarıya daima pozitif olarak çıkar. Buna göre; |4| | 3| |5| 4 3 5 2 bulunur. D oğru Cevap : B şıkkı 2) x 0 y z olmak üzere |x y| |z y| |z y| ifadesinin eşiti aşağıdakilerden hangisidir? A) x y B) x y C) x z D) x y E) x z ÇÖZÜM: negatif pozitif pozitif Mutlak değer içerisindeki değer, negatif ise ile çarparak dışarı çıkılır. Diğer durumlarda aynen dışarı çıkartılır. x 0 y z |x y| |z y| |z y| (x y) (z y) (z y) x y z y z y x y Doğru Cevap : D şıkkı 3) 2 x 4 olmak üzere, |x 6| |x 3| |4 x| ifadesinin eşiti aşağıdakilerden hangisidir? A) 2x 1 B) 1 x C) 13 x D) x 3 E) 2x 13 ÇÖZÜM: negatif pozitif pozitif x < 4 x > 2 x 4 Mutlak değerlerin içindeki ifadelere bakalım. Negatif olanları ile çarparak mutlak değerden çıkaralım. 2 x 4 olmak üzere, |x 6| |x 3| |4 x| (x 6) (x 3) (4 x) x 6 x 3 4 x 13 x bulunur. Doğru Cevap : C şıkkı 4) 2 x 3 olduğuna göre, ||x 2| 1| ||x 2| 5| ifadesinin eşiti aşağıdakilerden hangisidir? A) 2 B) x 2 C) 2x 10 D) 2x 4 E) 10 ÇÖZÜM: pozitif pozitif x 2 x 2 pozitif negatif x 2 x 3 İlk önce, en içerideki mutlak değerleri dışarı çıkarmaya çalışalım. 2 x 3 olduğuna göre, ||x 2| 1| ||x 2| 5| |x 2 1| |x 2 5| |x 1| |x 3| x 1 3 x 2 bulunur. Doğru Cevap : A şıkkı 5) x 0 olduğuna göre, x ||2x| 3x| | 2x| ifadesinin eşiti aşağıdakilerden hangisidir? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net ÇÖZÜM: Mutlak değerli ifadeleri dışarıya çıkarmaya çalışarak çözüme gidelim. x 0 olduğuna göre, x ||2x| 3x| x | 2x 3x| | 2x| | 2x| x | 5x| x 5x 4x 2 buluruz. | 2x| 2x 2x Doğru Cevap : B şıkkı 6) 2 2 1 x 2 olmak üzere x 2x 1 x 4x 4 işleminin sonucu kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: 2 2 2 2 Köklü ifadeler içerisinde yer alan ifadelerin tam kare ifadeler olduğunu görüyoruz. Buna göre; x 2x 1 x 4x 4 (x 1) (x 2) Tam kare ifadeler, köklü ifadelerin dışına mutlak değer içerisinde çıkar 2 2 . Buna göre; (x 1) (x 2) |x 1| |x 2| 1 x 2 olmak üzere |x 1| |x 2| x 1 (x 2) x 1 x 2 3 buluruz. Doğru Cevap : C şıkkı 7) 2 x 3 |y 2| (z 5) 0 olduğuna göre, x y z toplamı kaçtır? A) 0 B) 1 C) 2 D) 3 E) 4 ÇÖZÜM: 0 Derecesi çift olan köklü ifadeler, Mutlak Değerli ifadeler ile Üssü çift olan ifadeler negatif olamaz. Soruda verilen eşitlik, 0′ a eşit olduğu için her bir terim 0’a eşit olmak zorundadır. x 3 |y 2 0 0 2| (z 5) 0 x 3 0 x 3 y 2 0 y 2 z 5 0 z 5 Buna göre; x y z 3 2 5 4 buluruz. Cevap: E şıkkı 8) 3.|x 4| 5 17 denklemini sağlayan x değerlerinin toplamı kaçtır? A) 5 B) 6 C) 7 D) 8 E) 10 ÇÖZÜM: 4 veya 4 Mutlak değerli ifadeyi yalnız bırakacak şekilde denklemi çözmeye başlayalım. 3.|x 4| 5 17 3.|x 4| 12 | x 4 | 4 Bu durumda iki seçenek vardır. x 4 4 x 4 4 x 8 x 0 Toplam: 8 0 8 buluruz. Doğru Cevap : D şıkkı 9) |x 3| |3 x| |2x 6| 24 denklemini sağlayan x değerlerinin toplamı kaçtır? A) 6 B) 8 C) 9 D) 12 E) 15 ÇÖZÜM: 1 2 Mutlak değerli ifadeleri birbirine benzeyecek şekilde yazıp, onları ortak paranteze almaya çalışalım. |x 3| |3 x| |2x 6| 24 |x 3| |( 1).(x 3)| |2.(x 3)| 24 |x 3| | 1|.|x 3| |2|.|x 3| 24 www.matematikkolay.net |x 3| |x 3| 2.|x 3| 24 |x 3|.(1 1 2) 24 |x 3|.4 24 |x 3| 6 x 3 6 veya x 3 6 x 9 x 3 Değerler toplamı: 9 ( 3) 6 buluruz. Cevap: A 10) |2x|+| 2x| 3|x| | 7x| 64 denklemini sağlayan x değerlerinin çarpımı kaçtır? A) 48 B) 64 C) 80 D) 88 E) 92 ÇÖZÜM: |2x| | 2x| 3|x| | 7x| 64 2.|x| 2.|x| 3.|x| 7.|x| 64 |x|.(2 2 3 7) 64 |x|.8 64 |x| 8 x 8 veya x 8 Değerler çarpımı: 8.( 8) 64 buluruz. Cevap: B
 Bu bölümde Mutlak Değer ile ilgili 22 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Mutlak Değer ile ilgili 22 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…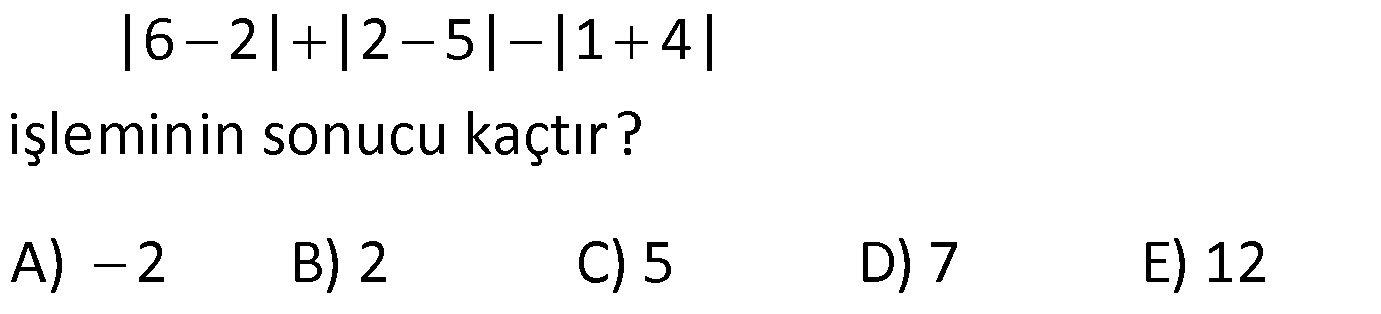

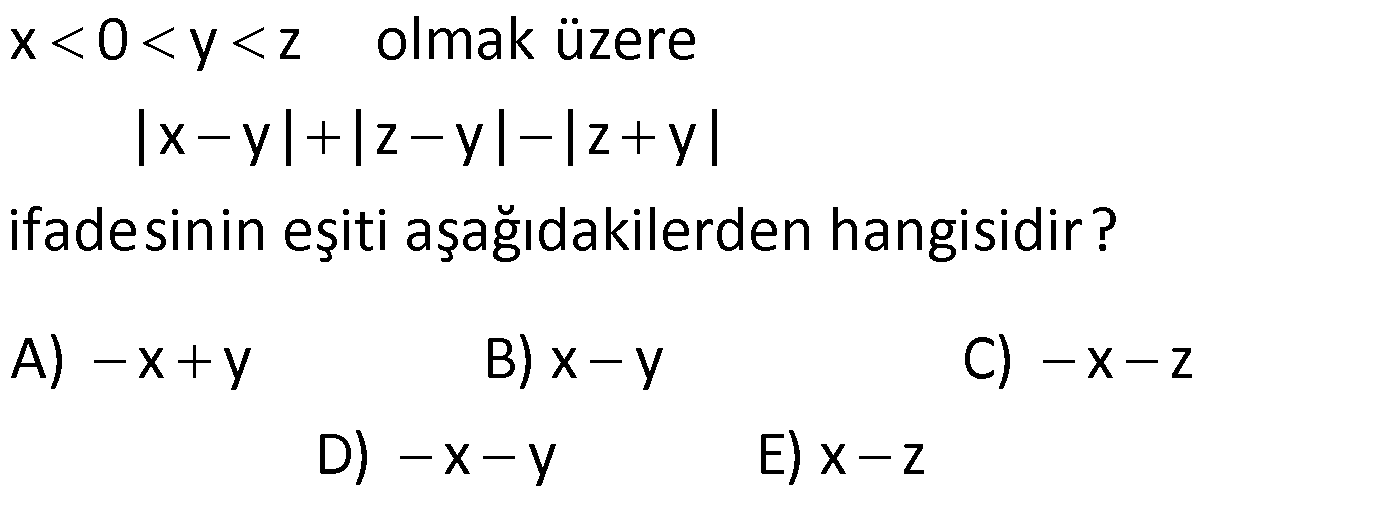

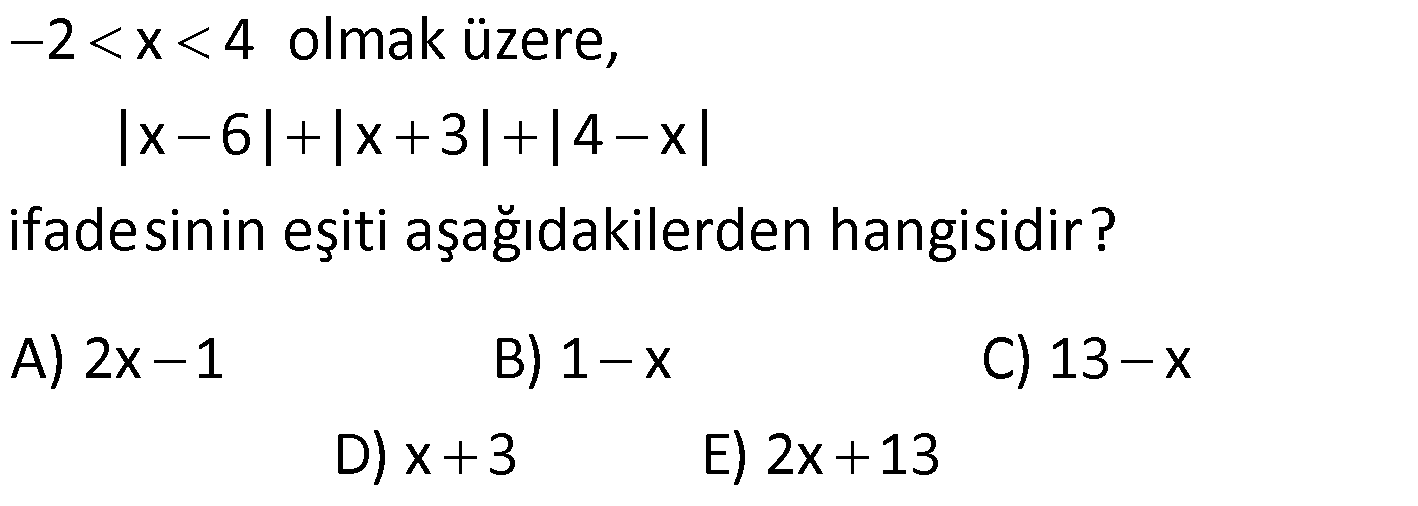

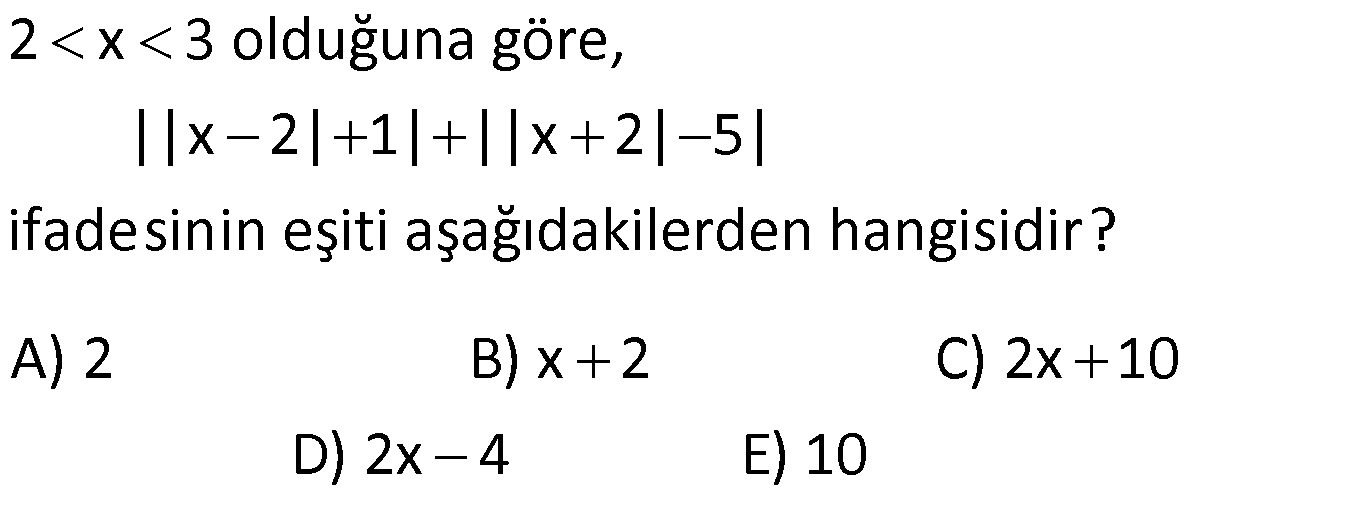




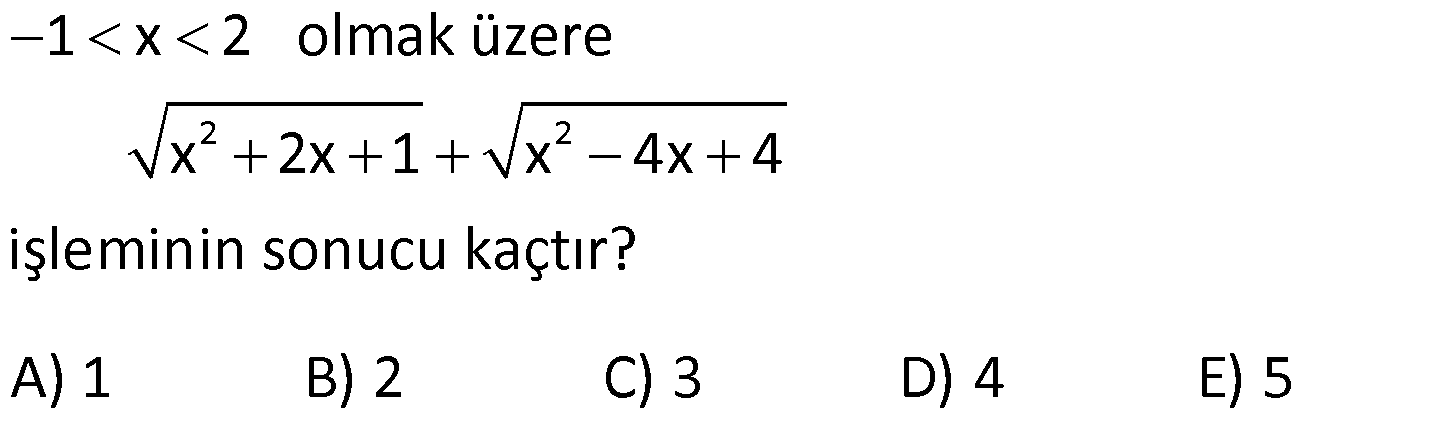

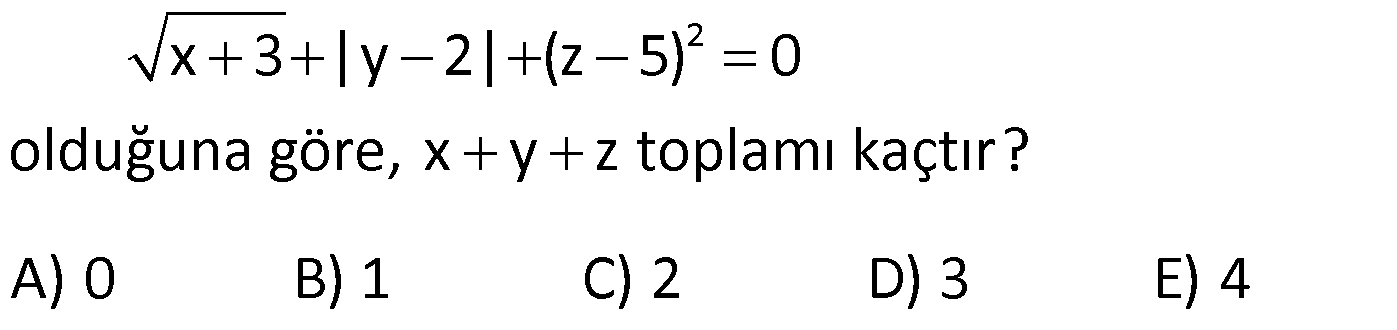

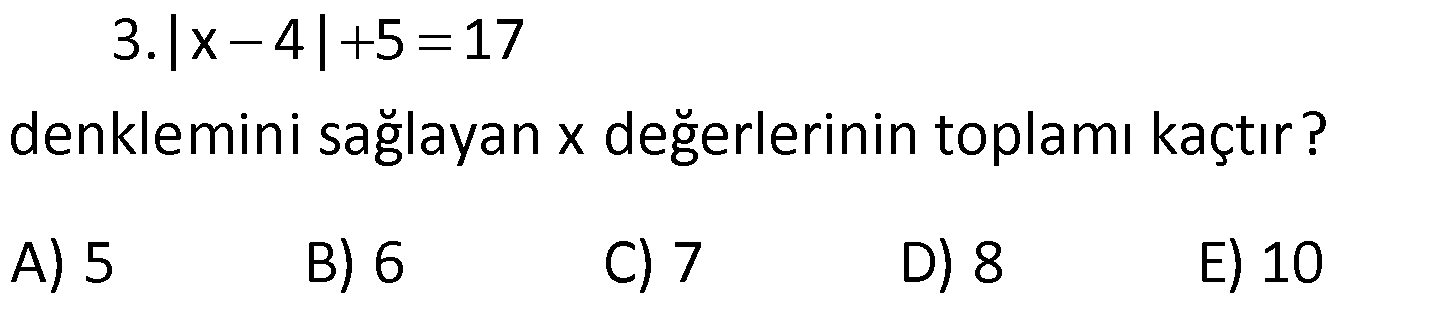

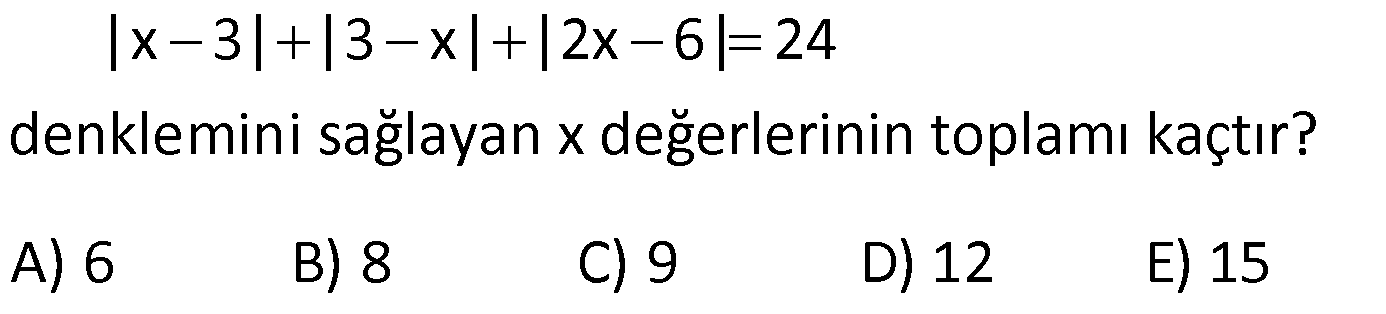


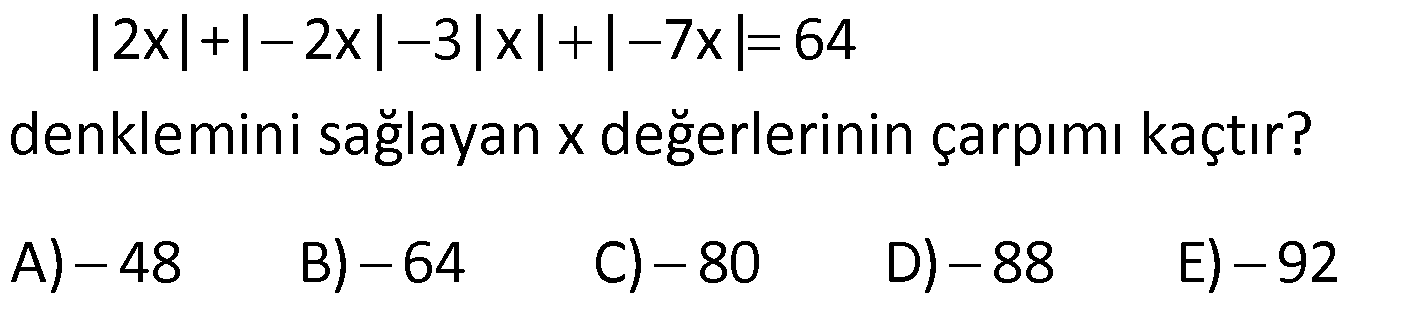




Hpcam size bir sorum olacak:
|2x-3|<5 olduğuna göre
|x+11|-3|x-1|-2|x-9|
ifadesinin değeri kaçtır?
Buradan soru çözümü yapmıyoruz. Bu sebeple yardımcı olamayacağız.
Forum tarzı küçük bir yer eklense insanlar birbirlerinin sorularına baksa güzel olabilir.
Güzel sorular var ama biraz easy sorular
1,2 soru hariç çokuzun sorular
İlk kez bu kadar güzel bir siteyle karşılaşıyorum ama konu anlatımında maddeler arası biraz daha boşluklu açık olsa tadından yenmez.MÜKEMMELSİNİZ
Gerçekten güzel sorular ben 12 sınıf öğrencisiyim normalde mutlak değer konusunu sevmiyordum ama konu anlatım dinledim ve bu siteden bu güzel soruları çözdüm çok faydalı oldu morel yükseltici sorular tekrar çok teşekkür ederim umarım yakında günlük soruları çözebilir hale gelirim…..
Soruların geneli kolay biraz daha zor olabilir.
5.sorunun cevabı hatalı değil mi?
“C” olması lazım sanırım
Hata bulamadık. B şıkkı doğru. İstersen x yerine -1 yazarak da test edebilirsin.
14. Soru x yerine 3 koy soru şöyle olur 3.3+3=12 bu yanlış mı olur kafam iyice karıştı
x=3 olursa 3.3-|3|=9-3=6 olur yani 12’ye eşit olmaz. Bu sebeple x=3 değerini alamayız.
Bildiğime göre tam sayılara 0’ı eklemiyoduk fakag 18. Soruda cevabın içinde 0 da var.Acaba ben mi yanlış anlamışım
18. Sorunun cevabı hakkında bir yorum yapmıştım ama herhangi bir yanlışlık yok,araştırdım.
Kolay gelsin
14.soruda neden 3 çözüm kumesine alinmamis??
Çünkü denklemi sağlamıyor.
HOCAM 2.SORUDA ZATEN X NEGATİF DEĞERİNDEDİR 0’DAN KÜÇÜK OLDUĞU İÇİN MUTLAK DEĞER İÇİNDE BELİRTMESEDE ÖYLE OLMASI GEREKMİYOR MU DAHA SONRA ZATEN EKSİ EKSİ ÇARPIMI ARTI OLUCAK VE CEVABIN X-Y OLMASI GEREKMİYOR MU?CEVAPLARSANIZ SEVİNİRİM HATAM VARSA DÜZELTMİŞ OLURUM.
x negatiftir doğru. Ancak, mutlak değerin içini bir bütün olarak düşünmeliyiz. |x-y| ifadesinde ilk önce x-y nin pozitif mi negatif mi olduğunu düşüneceğiz. x negatif, y de pozitif olduğu için bu çıkartma işlemi her zaman negatiftir. Mutlak değerin içindeki ifade negatifse tüm ifade – ile çarpılarak dışarı çıkarılırdı. Bu sebeple -(x-y) den -x+y olur.
Yani x-y olmaz.
Adminden nefret ediyorum çok itici ama site de mükemmel ötesi beni zor durumda bırakıyorsunuz hocam
Sorular iyi 💎lakin 6. Sorudaki x in yerine gelen sayı -1olması gerekmiyormu?
Soruda x in -1 ile 2 arasında olduğu söylenmiş. Yani bu aralıkta herhangi bir değer olabilir. Mesela x=0 da olabilir, x=1 de olabilir. Aralığın tamamını düşünerek soruyu çözmek lazım.
Ancak, bu soruya özel olarak x yerine -1 yazarsanız da doğru cevabı verecektir. Tabi, çözüm yolu doğru olmaz.
çok beğendim soruları çok yardımcı oldu sağol un
-4
Bence basit sorular
Hocam 21 ve 22. sorularda x’ e neye göre aralık veriyoruz, açıklar mısınız?