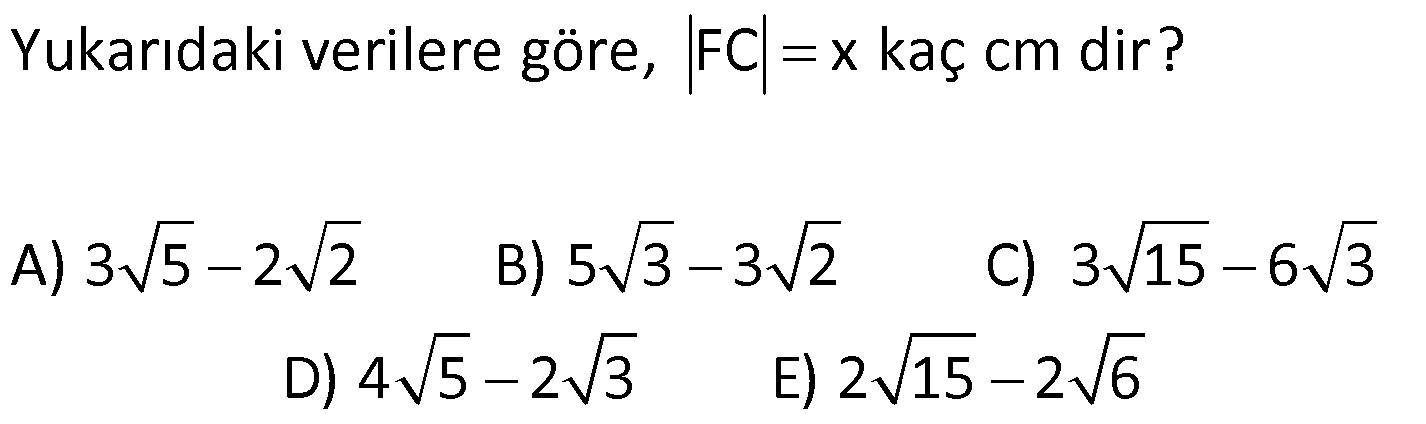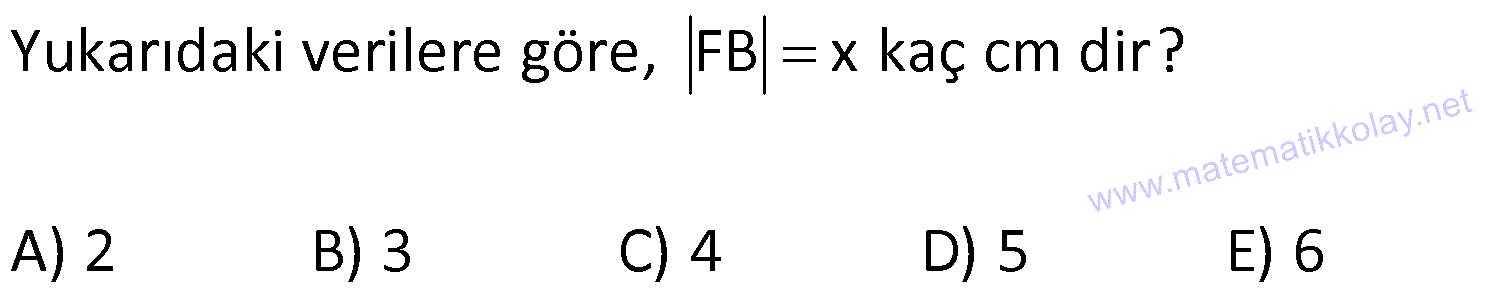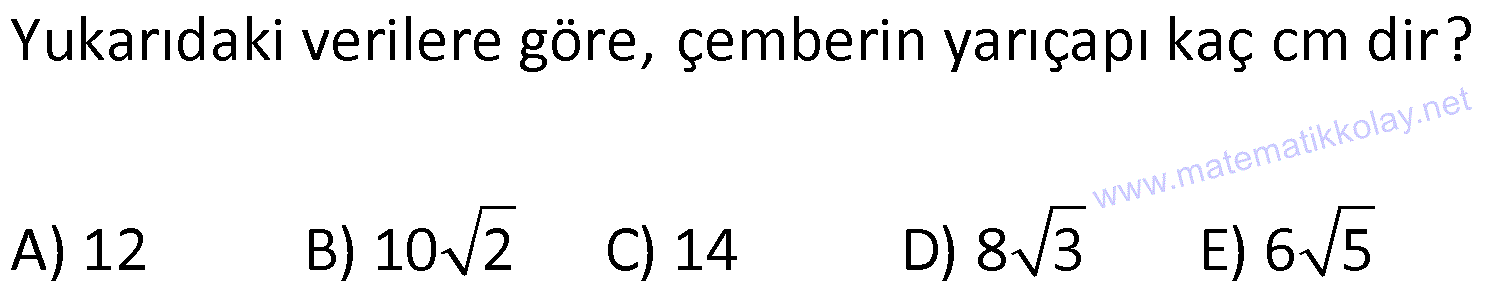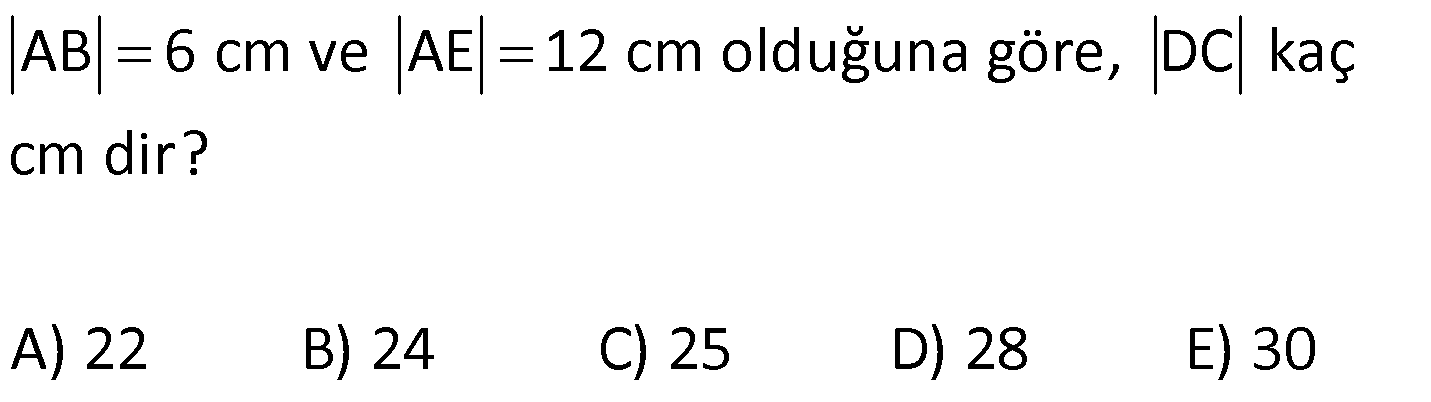 Bu bölümde Çemberde Teğet ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Çemberde Teğet ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
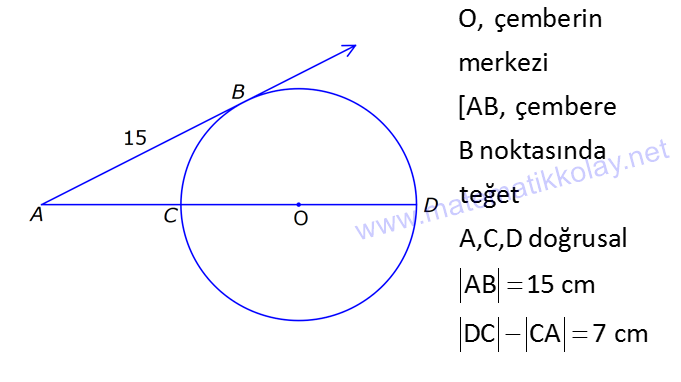
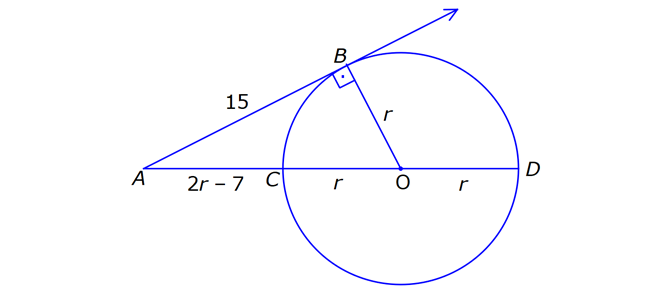
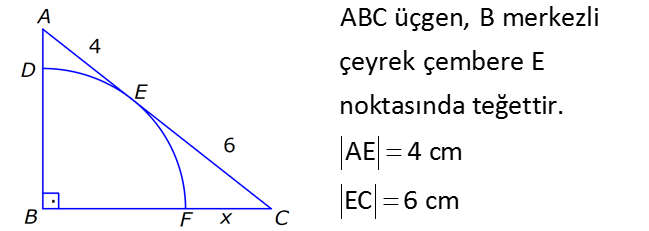
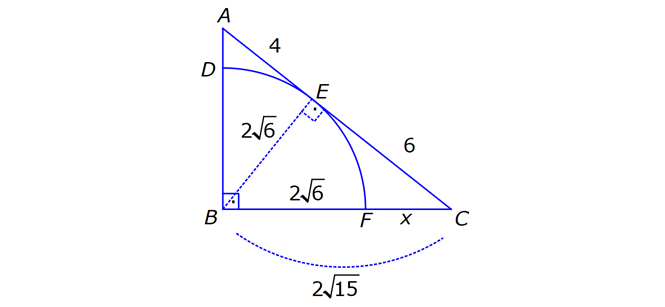
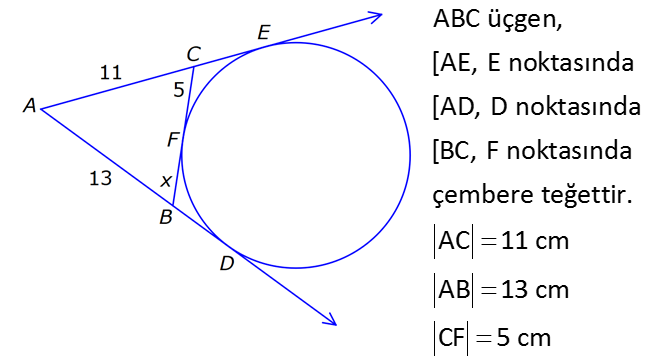
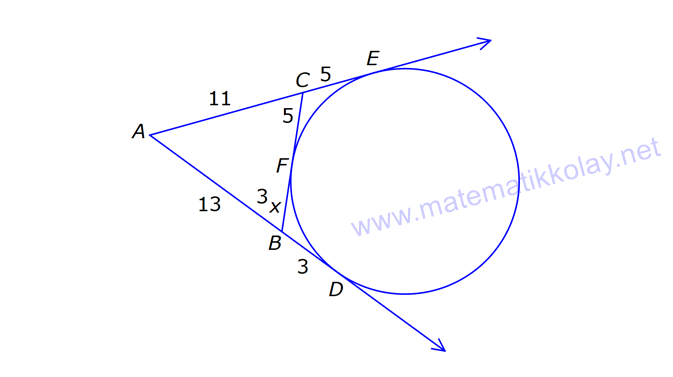
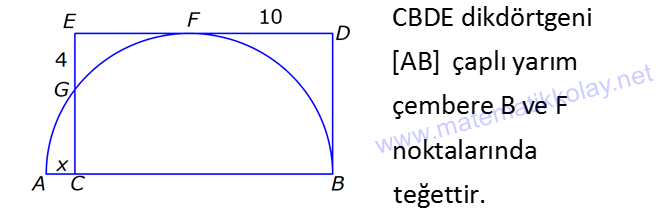
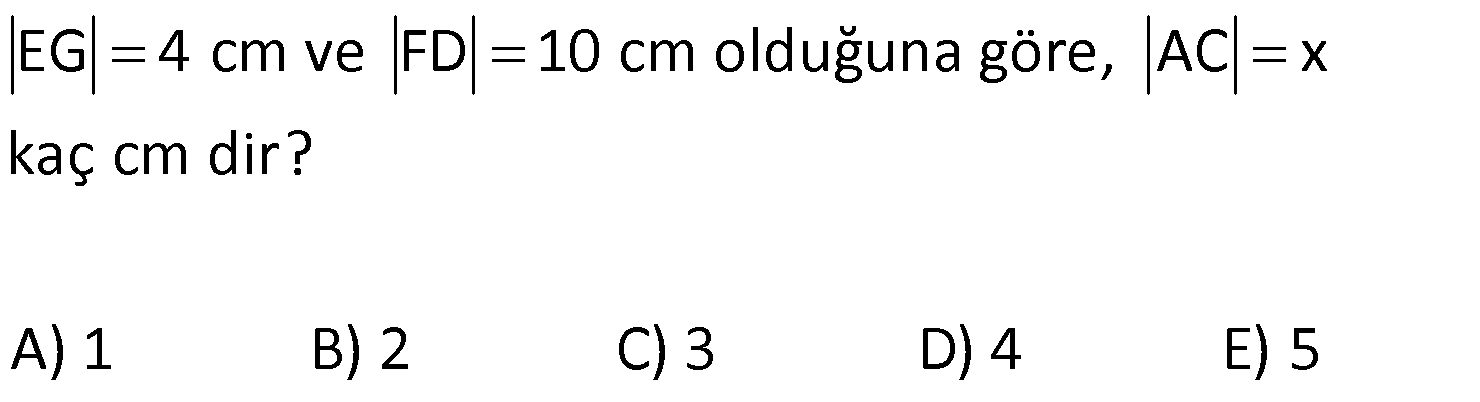
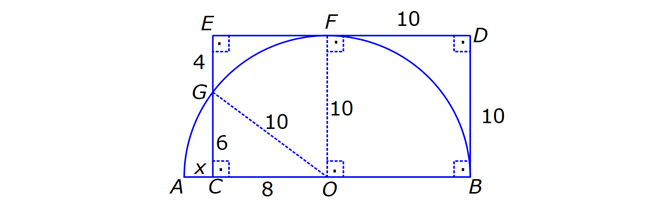
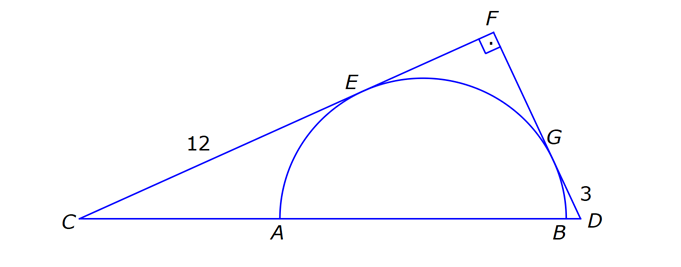
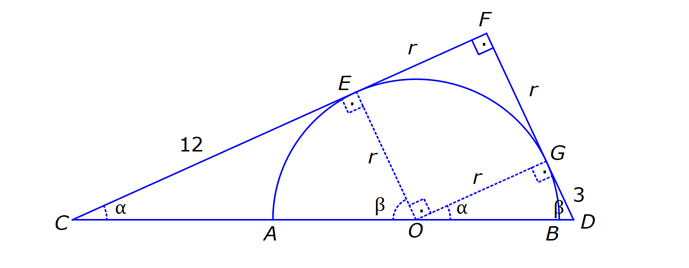
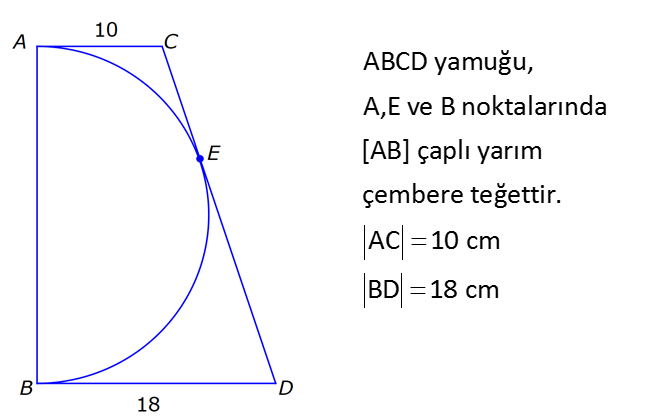
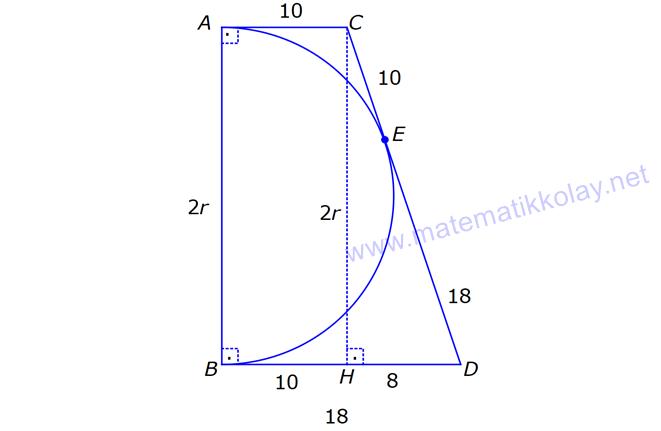
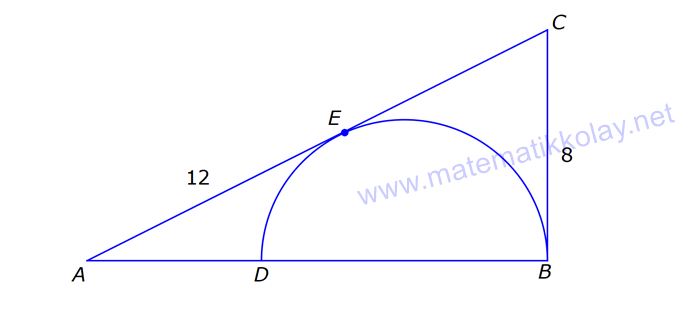
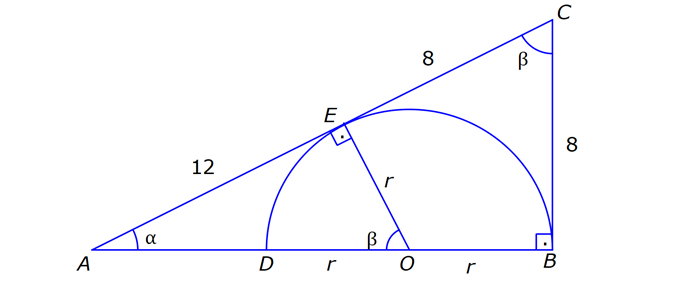
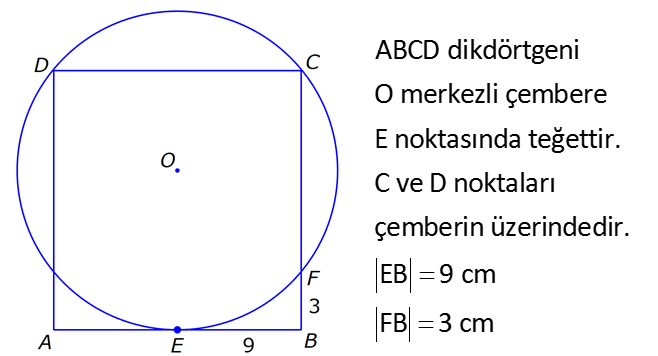
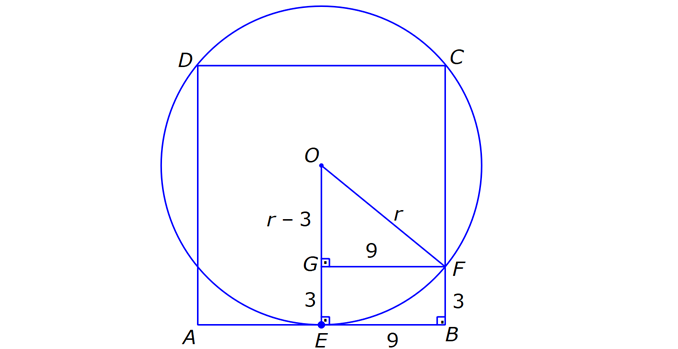
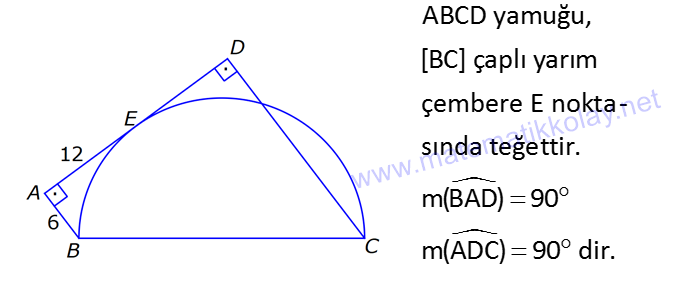
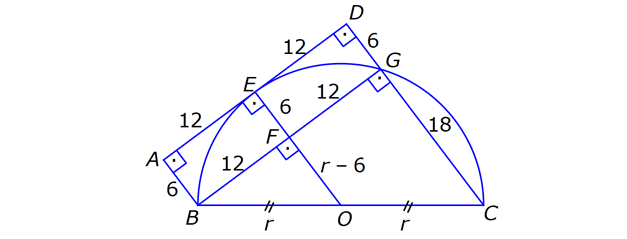
ÇEMBERDE TEĞET www.matematikkolay.net 1) O, çemberin merkezi [AB, çembere B noktasında teğet A,C,D doğrusal AB 15 cm DC CA 7 cm Yukarıdaki verilere göre, çemberin yarıçapı kaç cm dir? A) 8 B) 9 C) 10 D) 11 E) 12 ÇÖZÜM: Çemberin merkezi ile teğet noktasını birleş- tiren yarıçap, teğet doğrusuna diktir. Buna göre, [OB] [AB dir. DC 2r olduğuna göre, CA 2r 7 cm olmalıdır. ABO dik üçgeninde pisagor yapars Not: 2 2 2 2 2 2 2 2 2 4r 11 r 8 r 8 ak, r 15 (2r 7 r) r 225 (3r 7) r 225 9r 42r 49 0 8r 42r 176 her tarafı 2 ye bölelim. 0 4r 21r 88 0 (4r 11)(r 8) r 8 cm dir. Cevap : A (Dik üçgenin 8 -15-17 üçgeni olduğu nu tahmin edilerek de r 8 cm bulunabilir.) 2) ABC üçgen, B merkezli çeyrek çembere E noktasında teğettir. AE 4 cm EC 6 cm Yukarıdaki verilere göre, FC x kaç cm dir? A) 3 5 2 2 B) 5 3 3 2 C) 3 15 6 3 D) 4 5 2 3 E) 2 15 2 6 ÇÖZÜM: 2 2 2 2 2 2 2 Çemberin merkezinden E’ye dikme indirelim. Öklitten, BE 4.6 BE 24 BE 2 6 cm dir. Çemberin yarıçapı 2 6 cm olur. BEC üçgeninde pisagordan BC (2 6) 6 BC 24 36 BC 60 BC 60 2 15 cm dir. O hal de, x 2 15 2 6 cm dir. Cevap :E www.matematikkolay.net 3) ABC üçgen, [AE, E noktasında [AD, D noktasında [BC, F noktasında çembere teğettir. AC 11 cm AB 13 cm CF 5 cm Yukarıdaki verilere göre, FB x kaç cm dir? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: Çemberin dışındaki bir noktadan çembere çizilen teğetlerin uzunlukları birbirine eşittir. Buna göre, CE CF 5 cm dir (C noktasından çizilen teğetler). AE 11 5 16 cm olur. O halde, AD 16 Not: cm dir (A noktasından çizilen teğetler). BD 16 13 3 cm kalır. O halde, x 3 cm dir (B noktasından çizilen teğetler). Cevap:B 4) CBDE dikdörtgeni [AB] çaplı yarım çembere B ve F noktalarında teğettir. EG 4 cm ve FD 10 cm olduğuna göre, AC x kaç cm dir? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: FD 10 cm ise BD 10 cm dir (D noktasından çizilen teğetler birbirine eşit olmalıdır). Çemberin merkezi O noktası olsun. O’dan F’ye çizdiğimiz doğru, dik olacaktır. B ve D noktalarında da dik açı vardır (Dikdörtgenin köşeleri). O halde, O noktasında da dik açı olur. Yani OBDF dörtgeni bir karedir. OB OF 10 cm dir (yarıçap). GC 10 4 6 cm olur. [OG] yi çizelim. OCG üçgeni bir 6 – 8 -10 üçgeni olur. CO 8 cm dir. B una göre, x 10 8 2 cm buluruz. Cevap : B www.matematikkolay.net 5) CFD üçgeni, [AB] çaplı yarım çembere E ve G noktalarında teğettir. CE 12 cm ve GD 3 cm olduğuna göre, çemberin yarıçapı kaç cm dir? A) 4 B) 5 C) 6 D) 8 E) 9 ÇÖZÜM: Çemberin merkezi O noktası olsun. Teğet noktalarına şekildeki gibi dikmeler çizebiliriz. E,F,G noktalarında dik açı olduğuna göre, OGFE dörtgeninin diğer iç açısı da dik açı olacaktır. Bu dikdörtgenin ardışık iki kenarı da yarıçapa ait olduğundan bu bir kare olacaktır. OE OG EF FG r dir. m(ECO) ve m(EOC) olsun ( 90 ). m(DOG) ve m(OGD) olur ( 90 ). O halde, CEO üçgeni ile OGD üçgeni arasında 2 benzerlik yapabiliriz. r 3 r 36 r 6 cm dir. Cevap : C 12 r 6) ABCD yamuğu, A,E ve B noktalarında [AB] çaplı yarım çembere teğettir. AC 10 cm BD 18 cm Yukarıdaki verilere göre, çemberin yarıçapı kaç cm dir? A) 12 B) 10 2 C) 14 D) 8 3 E) 6 5 ÇÖZÜM: AC 10 cm ise CE 10 cm olmalıdır. BD 18 cm ise CD 18 cm olmalıdır. A ve B teğet noktalarında 90 lik açı olur. [CH] dikmesini indirelim. BH 10 cm olur. HD 8 cm kalır. CHD üçgeni 2 2 2 2 2 2 nde pisagor yaparsak, (2r) 8 28 4r 64 784 4r 720 r 180 r 6 5 cm dir. Cevap : E 7) www.matematikkolay.net ABC üçgeni, [BD] çaplı yarım çembere B ve E noktalarında teğettir. AE 12 cm ve BC 8 cm olduğuna göre, çemberin yarıçapı kaç cm dir? 7 15 3 30 6 20 11 5 8 21 A) B) C) D) E) 3 4 5 6 7 ÇÖZÜM: 2 2 2 2 2 EC CB 8 cm dir (Bir noktadan çizilen teğetler birbirine eşittir.) AB uzunluğunu bulalım. 8 AB 20 64 AB 400 AB 336 AB 336 16.21 4 21 cm dir. Çemberin merkezi O noktası olsun. Buradan E nokta – sına bir dikm nın karş e çizelim. E ve B noktalarında dik açı olacaktır. m(BAC) ve m(AOE) olsun ( 90 dir). ABC üçgeninde de m(ACB) olur. ABC üçgeni ile AEO üçgeni arasında benzerlik yapabiliriz. AEO r ABC 8 ısı 12 3 4 nın karşısı 21 24 24 r 21 21 8 21 21 7 8 21 r cm dir. Cevap: D 7 8) ABCD dikdörtgeni O merkezli çembere E noktasında teğettir. C ve D noktaları çemberin üzerindedir. EB 9 cm FB 3 cm Yukarıdaki verilere göre, çemberin yarıçapı kaç cm dir? A) 10 B) 12 C) 13 D) 14 E) 15 ÇÖZÜM: www.matematikkolay.net 2 2 2 2 Çemberin merkezinden E noktasına dikme çizelim. OE r dir. F’den [OE] ye bir dikme çizelim. FB 3 cm olduğundan OG r 3 cm kalır. GF EB 9 cm dir. OF r olduğuna göre, OGF üçgeninde pisagordan (r 3) 9 r r 2 6r 9 81 r 90 6r r 15 cm buluruz. Cevap : E 9) O merkezli iki çember yanda gösterilmiştir. A ve B noktaları büyük çemberin üzerindedir. [AB] doğru parçası küçük çembere E noktasında teğettir. AB 24 cm dir. 1 2 1 2 C, D, O doğrusal ve CD 3 cm dir. Küçük çemberin yarıçapı r , büyük çemberin yarıçapı r olduğuna göre, r oranı kaçtır? r 10 13 15 17 23 A) B) C) D) E) 11 15 17 21 25 ÇÖZÜM: 1 1 Küçük çemberin yarıçapı r ise, büyük çemberin yarıçapı r 3 cm dir. O’dan E noktasına dikme indirelim (teğet noktası). [AB] doğru parçası büyük çember için bir kiriş olduğu için, indirdiğimiz dikme [A 2 2 2 1 1 2 1 B] yi iki eş parçaya ayırır. AE EB 12 cm olur. OBE dik üçgeninde pisagor yaparsak r 12 (r 3) r 2 1 144 r 1 1 1 6r 9 135 135 6r r 45 6 2 2 1 2 45 dir. 2 45 51 r 3 dir. O halde, 2 2 45 r 2 r 51 2 45 15 51 17 15 dir. Cevap : C 17 10) ABCD yamuğu, [BC] çaplı yarım çembere E nokta – sında teğettir. m(BAD) 90 m(ADC) 90 dir. AB 6 cm ve AE 12 cm olduğuna göre, DC kaç cm dir? A) 22 B) 24 C) 25 D) 28 E) 30 www.matematikkolay.net ÇÖZÜM: O’dan E’ye dikme indirelim (teğet noktası). [BG] yi çizelim. m(BGC) 90 olur (çapı gören çevre açı). [BG] // [AD] olduğu için F noktasında da dik açı olur. BF AE 12 cm dir. AB EF DG 6 cm dir. BO r ise FO 2 2 2 2 r 6 cm dir. BFO üçgeninde pisagor yaparsak, 12 (r 6) r 144 r 2 12r 36 r 180 12r r 15 cm dir. FO 15 6 9 cm dir. BGC üçgeninde [FO] orta taban olduğu için GC 2.9 18 cm dir. DC 6 18 24 cm buluruz. Cevap: B
 Bu bölümde Çemberde Teğet ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Çemberde Teğet ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…