Bu bölümde Çarpanlara Ayırma ile ilgili 37 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
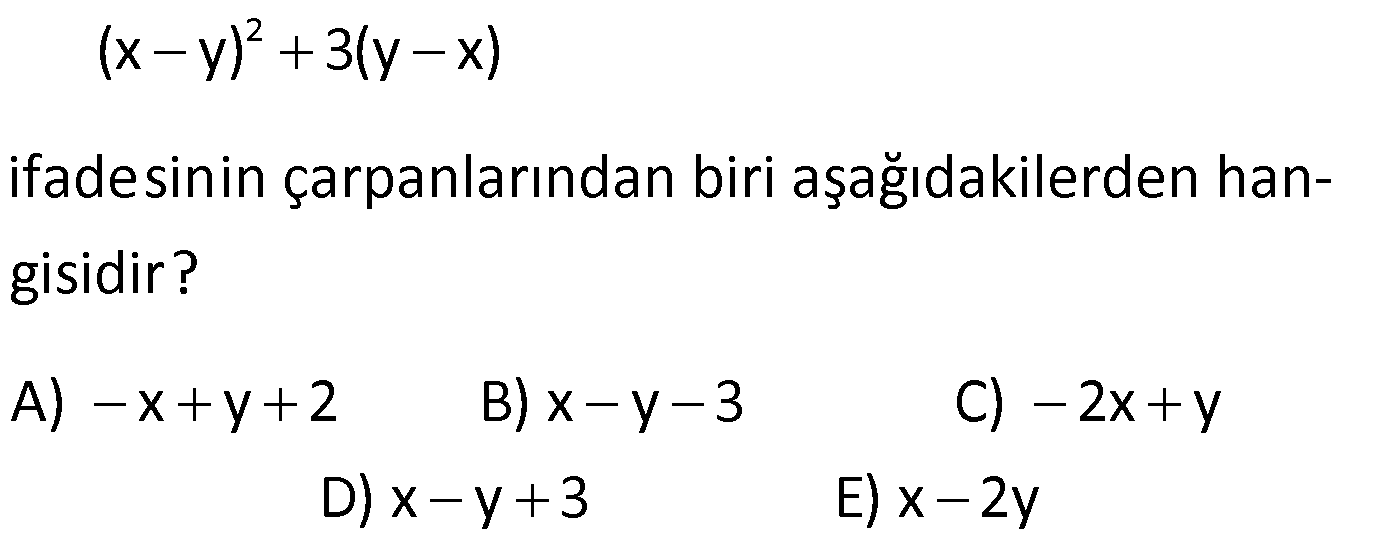
| | | | | |
Çözüm için Tıklayınız.

2.SORU

| | | | | |
Çözüm için Tıklayınız.

3.SORU
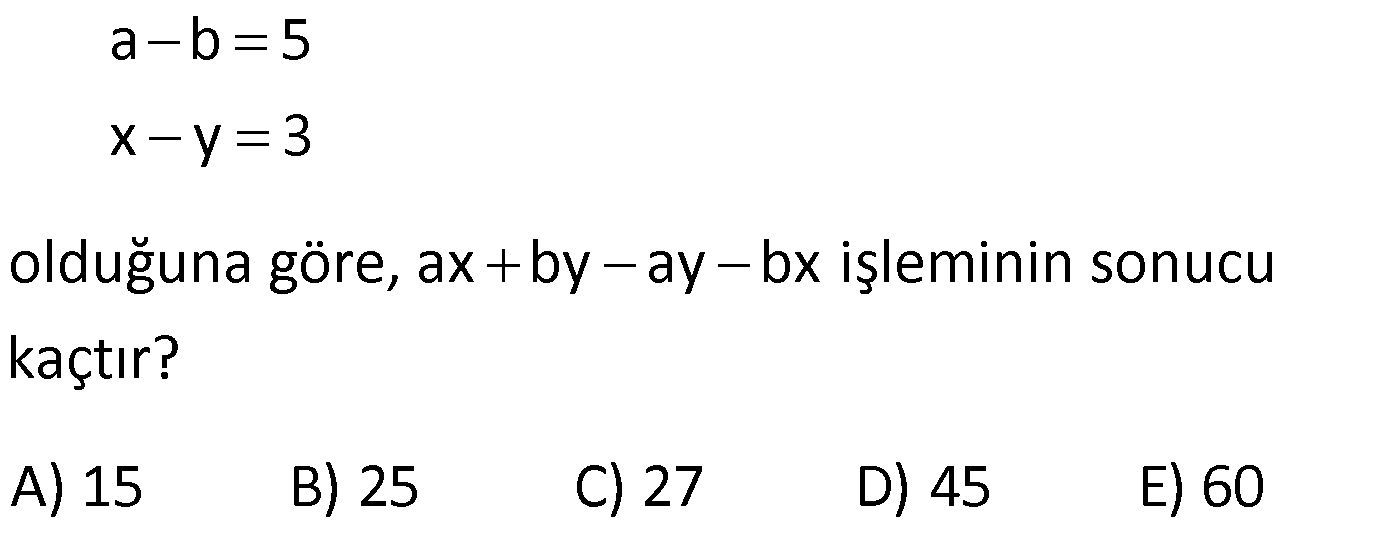
 | | | | |
Çözüm için Tıklayınız.
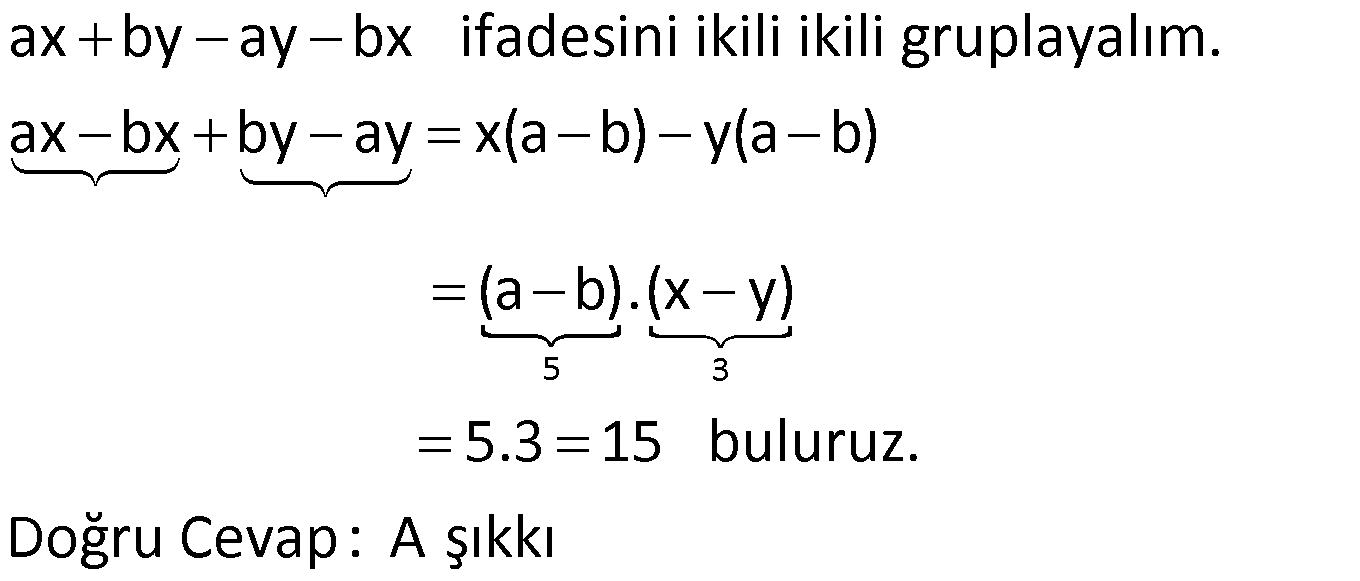
4.SORU

| | | | | |
Çözüm için Tıklayınız.

5.SORU
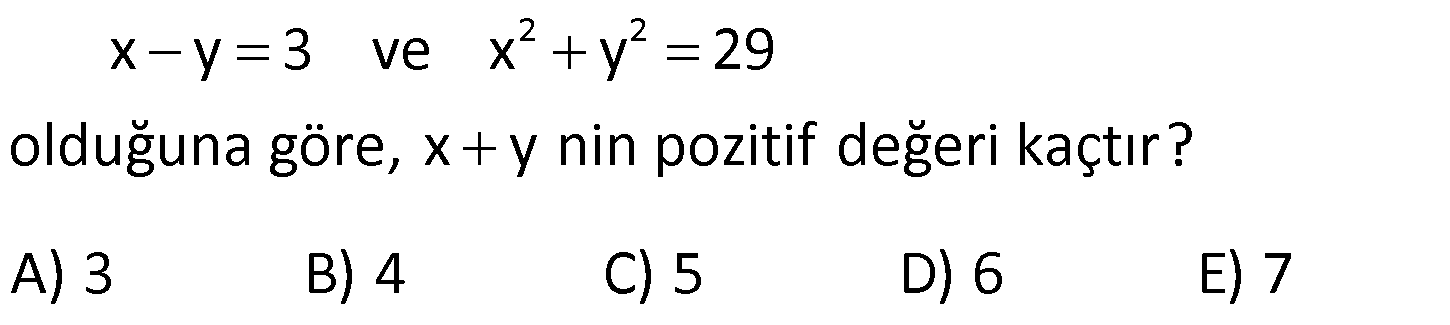
| | | | | |
Çözüm için Tıklayınız.

6.SORU
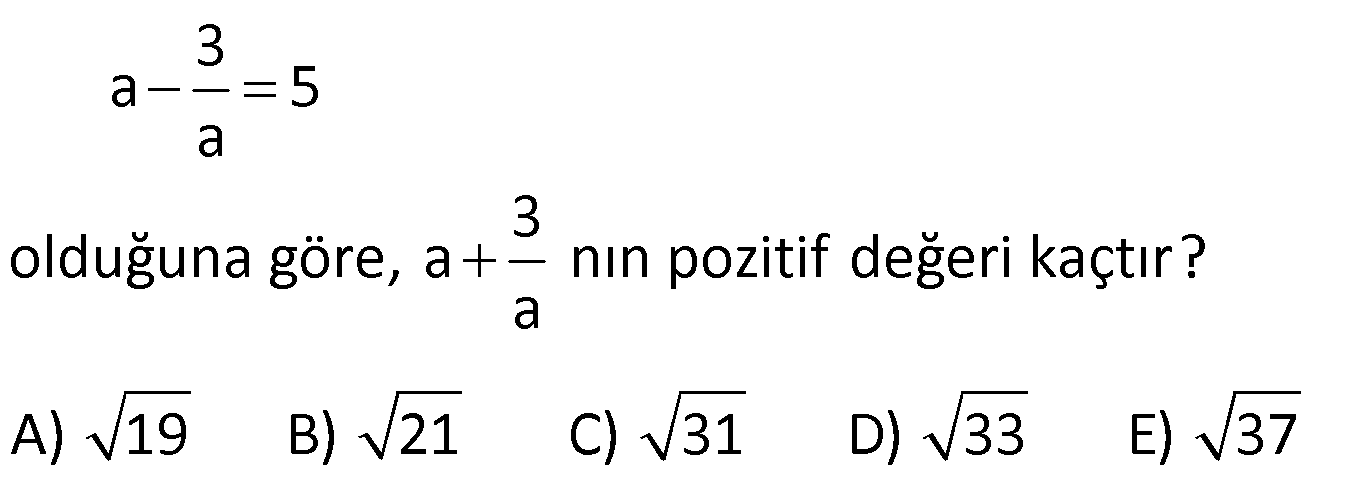
| | | | | |
Çözüm için Tıklayınız.

7.SORU
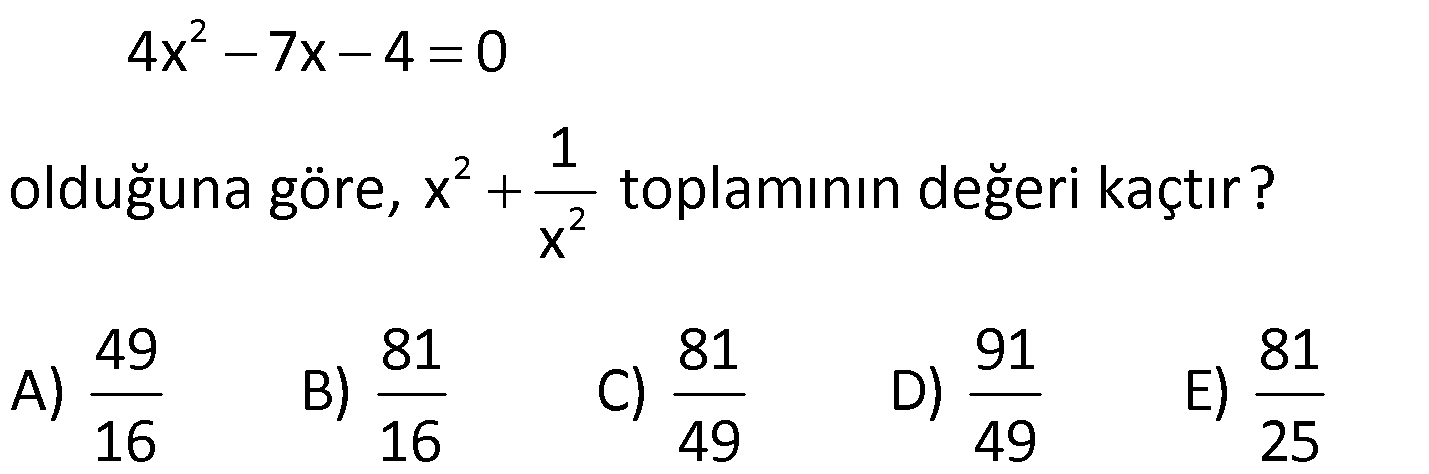
| | | | | |
Çözüm için Tıklayınız.

8.SORU
 | | | | |
Çözüm için Tıklayınız.

9.SORU
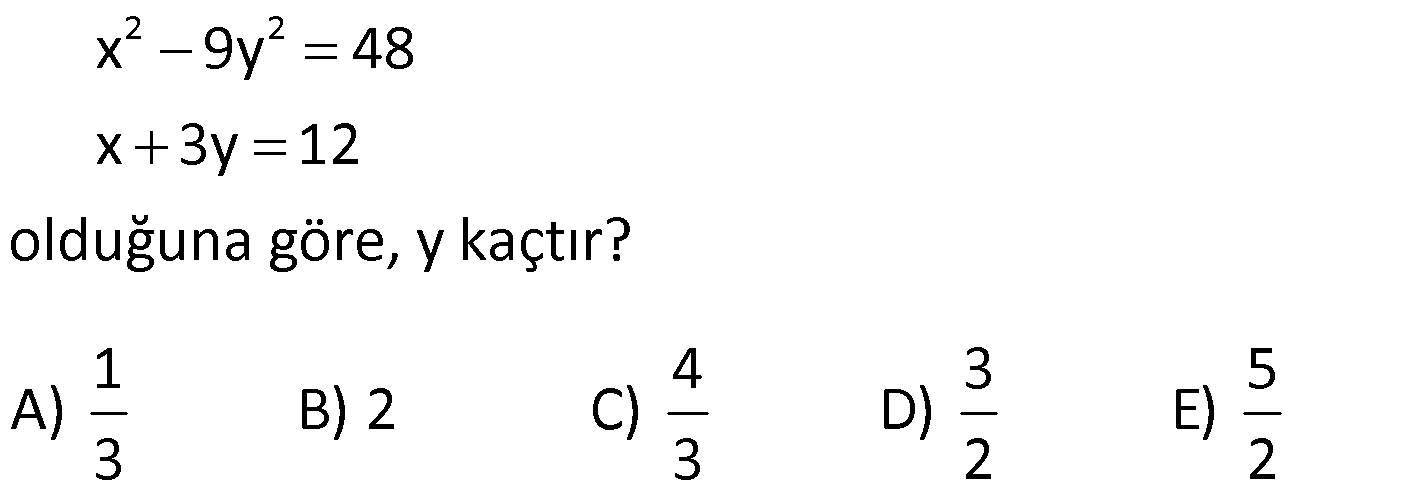
| | | | | |
Çözüm için Tıklayınız.
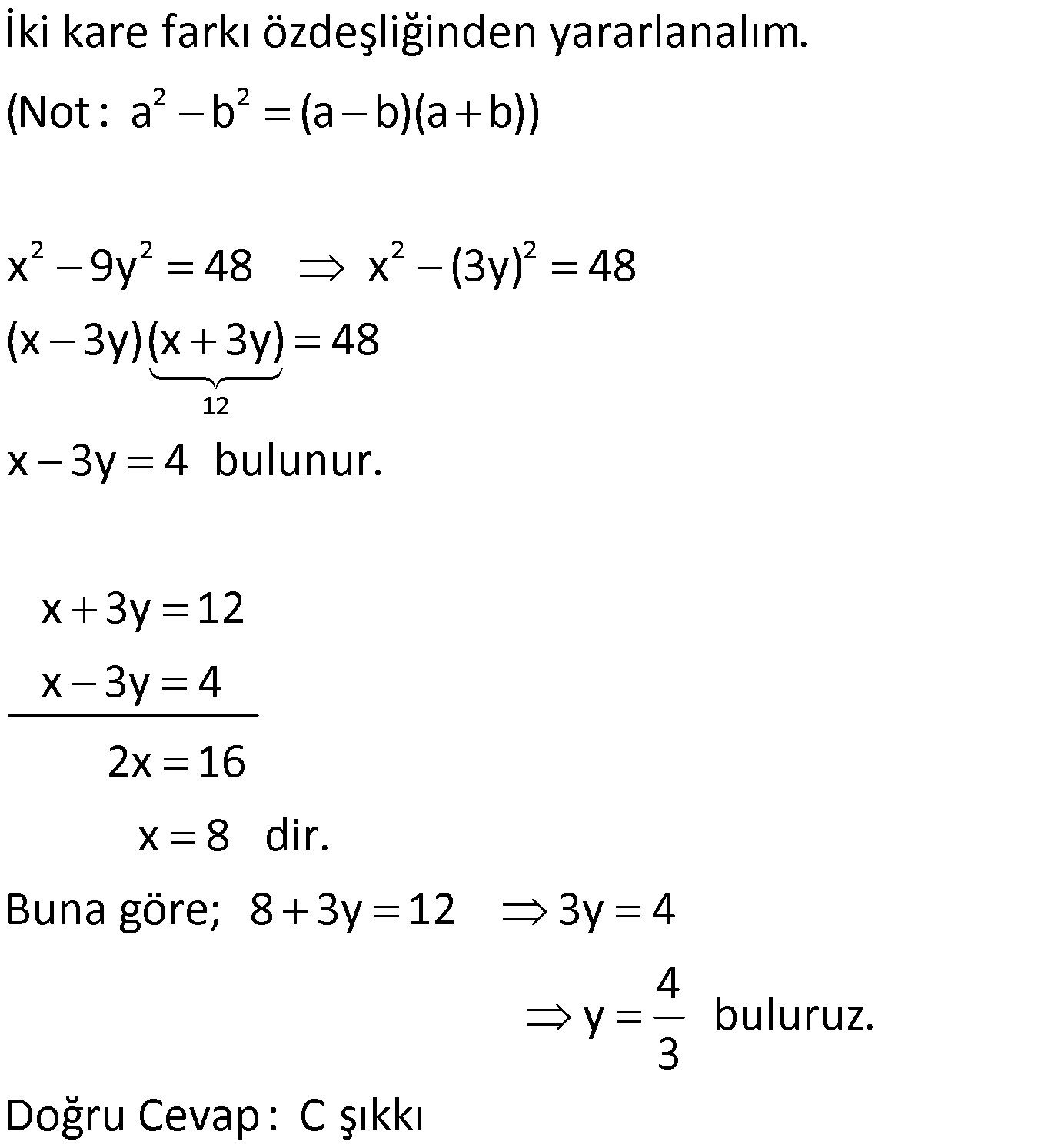
10.SORU
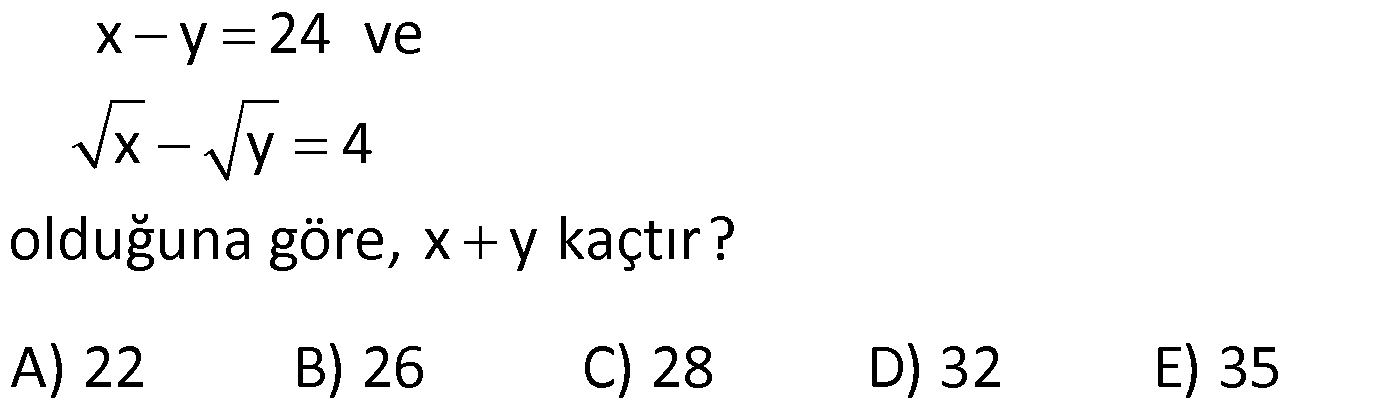
| | | | | |
Çözüm için Tıklayınız.
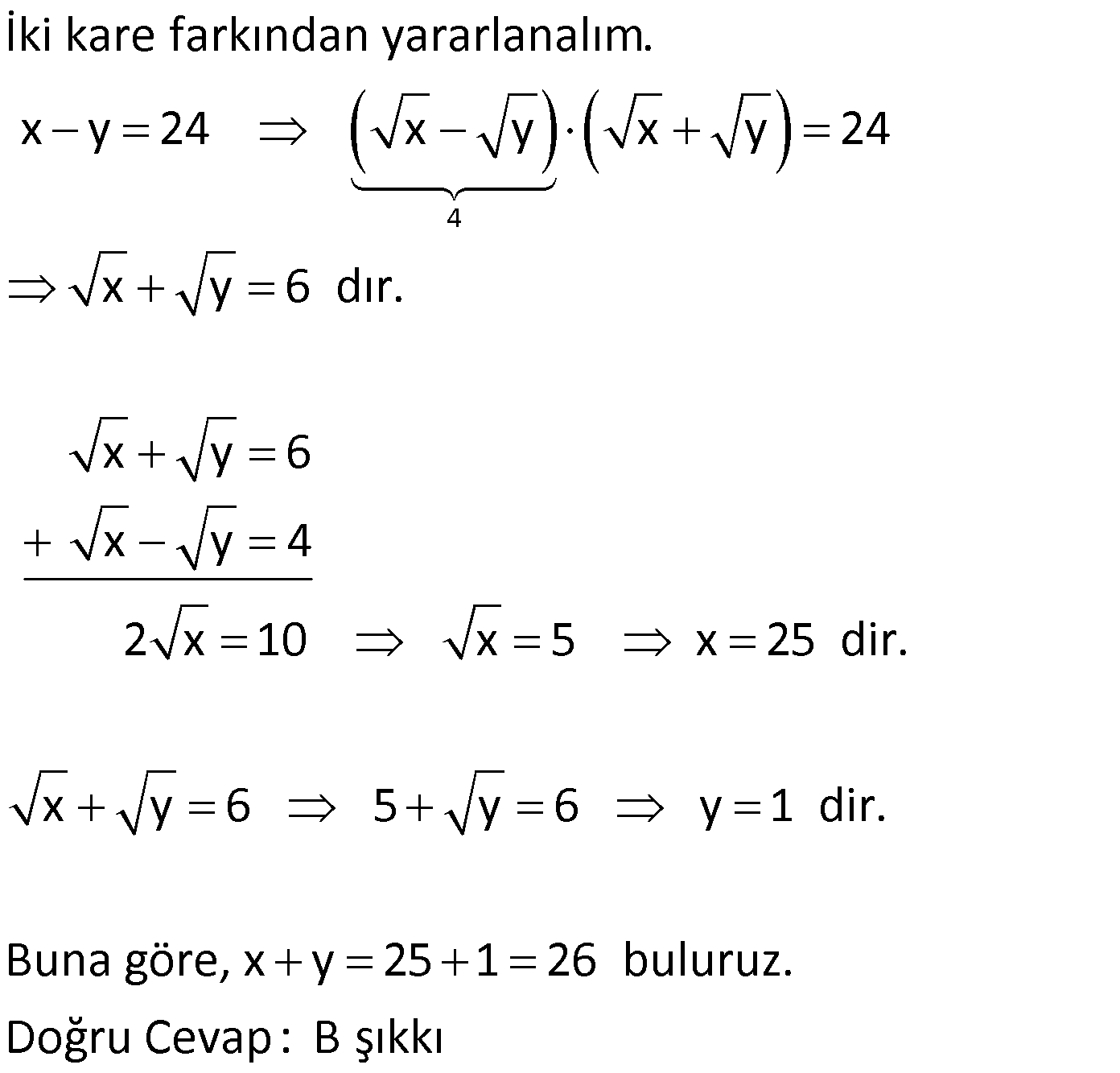
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
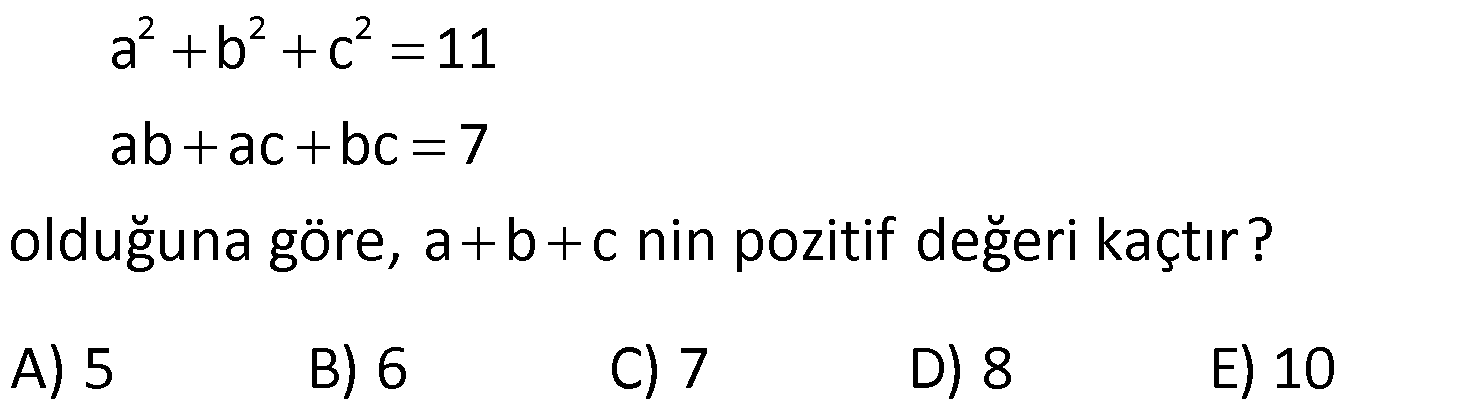
ÇARPANLARINA AYIRMA SORULARI VE ÇÖZÜMLERİ www.matematikkolay.net 1) 2 (x y) 3(y x) ifadesinin çarpanlarından biri aşağıdakilerden hangisidir? A) x y 2 B) x y 3 C) 2x y D) x y 3 E) x 2y ÇÖZÜM: 2 2 (x y) (x y) 3(y x) ifadesini düzenleyip, ortak paranteze almaya çalışalım. (x y) 3(y x) (x y)(x y) 3(x y) (x y) x y 3 B şıkkında x y 3 çarpanı var dır. Doğru Cevap : B şık kı 2) 6 4 2 3 4 4 4 2 a a a 1 ifadesinin çarpanlarından biri aşağıdakilerden hangisidir? A) a 1 B) a a C) a 1 D) a 1 E) a 1 ÇÖZÜM: 6 4 2 4 2 2 2 4 4 İfadeyi ikili ikili gruplandırarak çarpanlarına ayırmaya çalışalım. a a a 1 a (a 1) (a 1) (a 1)(a 1) bulunur. C şıkkında (a 1) çarpanı var. Cevap : C şıkkı 3) a b 5 x y 3 olduğuna göre, ax by ay bx işleminin sonucu kaçtır? A) 15 B) 25 C) 27 D) 45 E) 60 ÇÖZÜM: 5 3 ax by ay bx ifadesini ikili ikili gruplayalım. ax bx by ay x(a b) y(a b) (a b).(x y) 5.3 15 buluruz. Doğru Cevap : A şıkkı 4) 2 2 x xy 20 y xy 5 olduğuna göre, x y nin pozitif değeri kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: 2 2 2 2 2 Eşitliği taraf tarafa toplarsak, buradan x y nin karesini elde ederiz. x xy 20 y xy 5 x 2xy y 25 (x y) 25 ise x y 5 bulunur. Denklem sisteminde çıkarma yaparsak 2 2 2 2 5 , buradan iki kare farkı elde ederiz. x xy 20 – y xy 5 x y 15 (x y)(x y) 15 tir. Buradan da x y 3 bulunur. Doğru Cevap : C şıkkı 5) 2 2 x y 3 ve x y 29 olduğuna göre, x y nin pozitif değeri kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 www.matematikkolay.net ÇÖZÜM: 2 2 2 2 2 2 29 (x y) nin karesini alarak çözüme başlayalım. (x y) 3 (x y) 3 x 2xy y 9 x y 2xy 9 29 2xy 9 2 2 2 2 2 29 10 2xy 20 xy 10 dur. Şimdi (x y) nin karesini hesaplayabiliriz. (x y) x 2xy y x y 2xy 29 2.10 29 20 49 ( 2 x y) 49 x y 7 olabilir. Doğru Cevap : E şıkkı 6) 3 a 5 a 3 olduğuna göre, a nın pozitif değeri kaçtır? a A) 19 B) 21 C) 31 D) 33 E) 37 ÇÖZÜM: 2 2 2 2 2 2 2 2 Bu soruda tam kare özdeşliklerinden yararlanalım. 3 3 a 5 a (5) a a 3 3 a 2 a 25 a a 9 a 6 25 a 9 a 31 dir. a Soruda istenen 2 2 2 3 a ifadesinin karesini yukarıdaki a eşitlikten elde edebiliriz. 3 a ‘nın tam karesini yazalım. a 3 3 9 a a 2 a a a a 2 2 2 2 2 2 31 2 3 9 a a 6 a a 3 9 a a 6 a a 3 a 37 a 3 a 37 buluruz. Doğru Cevap : E şıkkı a 7) 2 2 2 4x 7x 4 0 1 olduğuna göre, x toplamının değeri kaçtır? x 49 81 81 91 81 A) B) C) D) E) 16 16 49 49 25 ÇÖZÜM: 2 2 2 2 2 2 2 2 2 2 Eşitliğin her iki tarafını 4x ‘e bölelim. 4x 7x 4 0 4x 4x 4x 7x 4 0 4x 4x 4x 7 1 x 0 4 x 1 7 x (Her iki tarafın karesini alalım.) x 4 1 7 x x 4 1 1 49 x 2 x x x 16 1 49 x 2 x 16 1 49 x x 2 2 2 16 1 49 32 81 x buluruz. x 16 16 Doğru Cevap : B şıkkı www.matematikkolay.net 8) 2 2 2 a b c 11 ab ac bc 7 olduğuna göre, a b c nin pozitif değeri kaçtır? A) 5 B) 6 C) 7 D) 8 E) 10 ÇÖZÜM: 2 2 2 2 2 2 2 2 11 7 2 2 2 3 terimli bir ifadenin tam karesini gösteren özdeşlikten yararlanalım. (a b c) a b c 2.(ab ac bc) (a b c) a b c 2.(ab ac bc) (a b c) 11 2.7 (a b c) 11 14 (a b c) 25 a b c 5 bul uruz. Doğru Cevap : A şıkkı 9) 2 2 x 9y 48 x 3y 12 olduğuna göre, y kaçtır? 1 4 3 5 A) B) 2 C) D) E) 3 3 2 2 ÇÖZÜM: 2 2 2 2 2 2 12 İki kare farkı özdeşliğinden yararlanalım. (Not : a b (a b)(a b)) x 9y 48 x (3y) 48 (x 3y)(x 3y) 48 x 3y 4 bulunur. x 3y 12 x 3y 4 2x 16 x 8 dir. Buna göre; 8 3y 12 3y 4 4 y buluruz. 3 Doğru Cevap : C şıkkı 10) x y 24 ve x y 4 olduğuna göre, x y kaçtır? A) 22 B) 26 C) 28 D) 32 E) 35 ÇÖZÜM: 4 İki kare farkından yararlanalım. x y 24 x y x y 24 x y 6 dır. x y 6 x y 4 2 x 10 x 5 x 25 dir. x y 6 5 y 6 y 1 dir. Buna göre, x y 25 1 26 buluruz. Doğru Cevap : B şıkkı



Acilimdan sonra neden x-y-3 oldu hiç anlamadım
Bir tarafta (x-y) nin katsayısı (x-y); diğer tarafta ise -3.
Bunları birleştirirsek x-y-3 olur.
7. soruda paydayı sıfır yapan değerler sadeleşmeyi sağlıyor diye aldık ancak paydanın sıfır olması tanımsız yapar, o değerleri neden aldık hocam. cevabınız için teşekkürler.
Biz paydayı 0 yapmıyoruz. Sadece ortak çarpanı yakalamak için 0’a eşitliyoruz. Çünkü pay ve paydada aynı çarpan olursa sadeleşme olur. Paydanın bir çarpanını 0 yapan x değeri, tüm paydayı 0 yapar. Aynı çarpan, pay’ın içinde de varsa, aynı x değeri orayı da 0 yapacaktır. Bu gerçekleşiyorsa aynı çarpan hem pay’da hem de payda da vardır. Bu sebeple sadeleşir. (2.Test 7.Soru)
34. soru -12 olacak
Uyarınız için teşekkürler. Yazım hatası yapılmış. Şimdi düzeltildi.
sorular ve çözümleri çok güzel. Ben teşekkür ederim 🙂
5.soru yanlış +29 u +9 yanına atıp -20 yerine +20 yazılmış
Hata yok. Sadece 2 işlem aynı anda yapılıyor. 29 karşı tarafa atılınca -2xy=-20 olur. Sonra her iki tarafı – ile çarpınca 2xy=20 olur.
Neden 1.sorudaki çözüm kısmında, -3.(x-y)’de dağıtma işlemi yapmadınız?
Diğer taraftaki x-y ile ortak paranteze alabilmek için
gayet güzel sorulardı çok beğendim elinize sağlık
Hocam a+b+c’2 = 25 ama, bunları bölemiyoruz edemiyoruz nasıl a+b+c 5 buldunuz 5 bölmeniz lazım yada neyin karesi 25 > 5 olur böylede olur ama benim anlamadığım a+b+c 5 nasıl oldu tamam 5 in karesi 25 ama parentezden aldıgımız zaman 5 nasıl kalıyor bölmüyoruz etmiyoruz
Pozitif değerler için düşünürsek, karesi 25 olan sayı 5 tir.
x^2=25 olsun x=5 tir.
(a+b+x)^2=25 olsun. Parantezin içi 5 tir. Yani a+b+x=5 tir. (Yapılan işlem bölme işlemi değil.)
(x+y+z)^2=49 olsun. x+y+z=7 dir.
Not: Sorudaki tüm ifadelerin pozitif olduğunu varsayarak bu örnekleri verdim.
Hocam shocam sorular çok güzeldi ama benim aklımı karıştıran bir soru var söyleyebilir miyim size ya sorulardan farklı bir şekilde 2 – 6 ortak çarpanlarına ayırın sorusunu hocam cevap ortak çarpan 4 olmuyor mu sadece bunu sormak istiyorum hocam çözümü ile beraber atar mısınız
Sayıları değiştirmeden ortak paranteze alacaksan, 2 parantezine alabilirsin.
2(1-3) olur.
1. soruda (x-y)^2 si ifadesi iki kare farkı özdeşliğinden (x-y).(x+y) olmazmı
İki kare farkı x^2-y^2 şeklindeki ifadelerdir.
(x-y)^2 ifadesi tam karedir. İki kare farkı değil. (x-y)(x-y) dir.
çok teşekkürler ya, çarpanlara ayırmadan ne kadar video izlesem, tüm formülleri bilsem de soruları çözemiyordum, daha doğrusu aklıma gelmiyordu üst üstte soru yapamayınca da, devam edesim gelmiyordu… İyii ki çözümlü yapmışsınız çok teşekkür ediyorum<3
Sorular kolaydı hepsi bundan ibaret+×÷=