Soru Sor sayfası kullanılarak Çarpanlara Ayırma konusu altında Değişken değiştirerek çarpanlarına ayırma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU

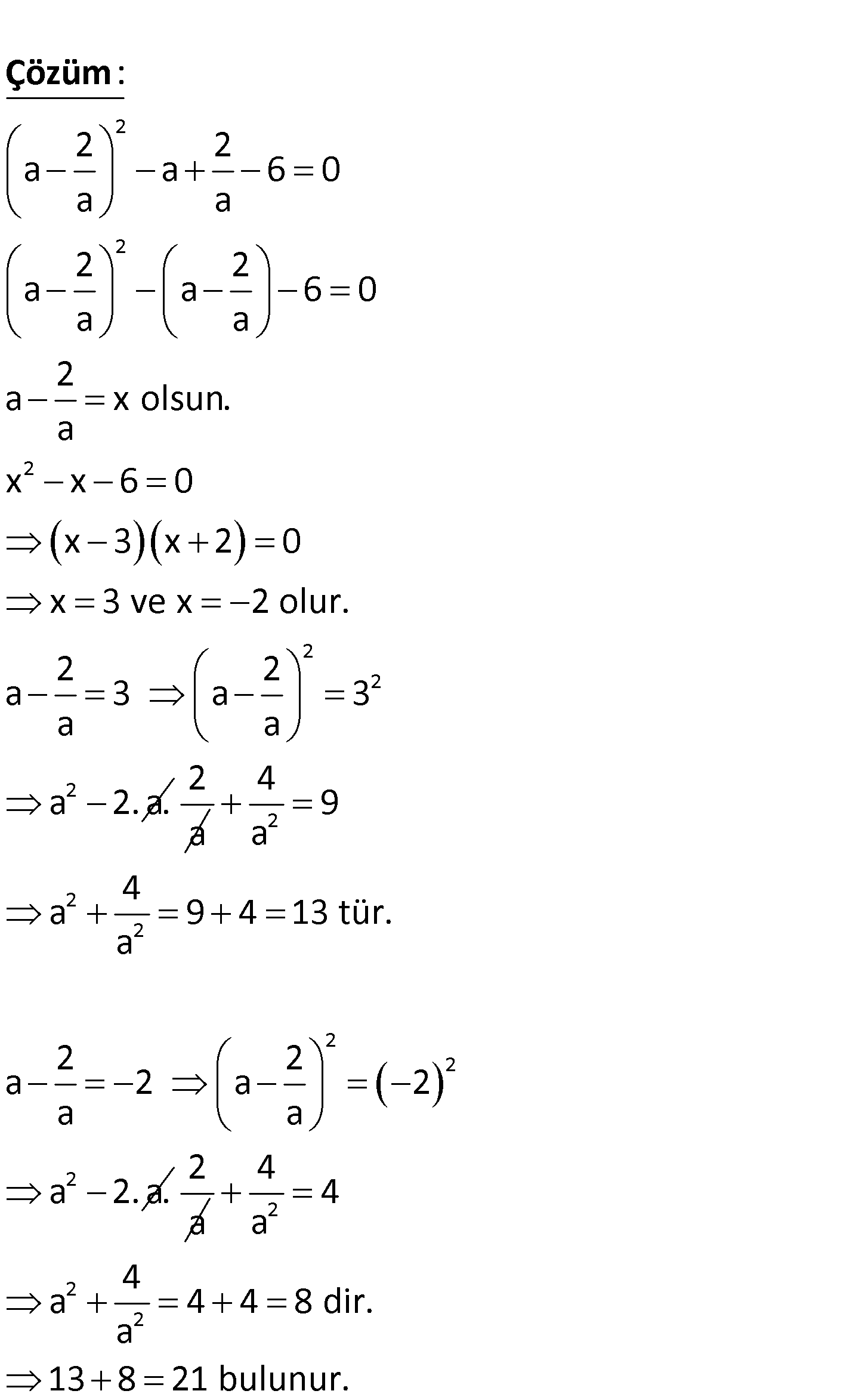
5.SORU

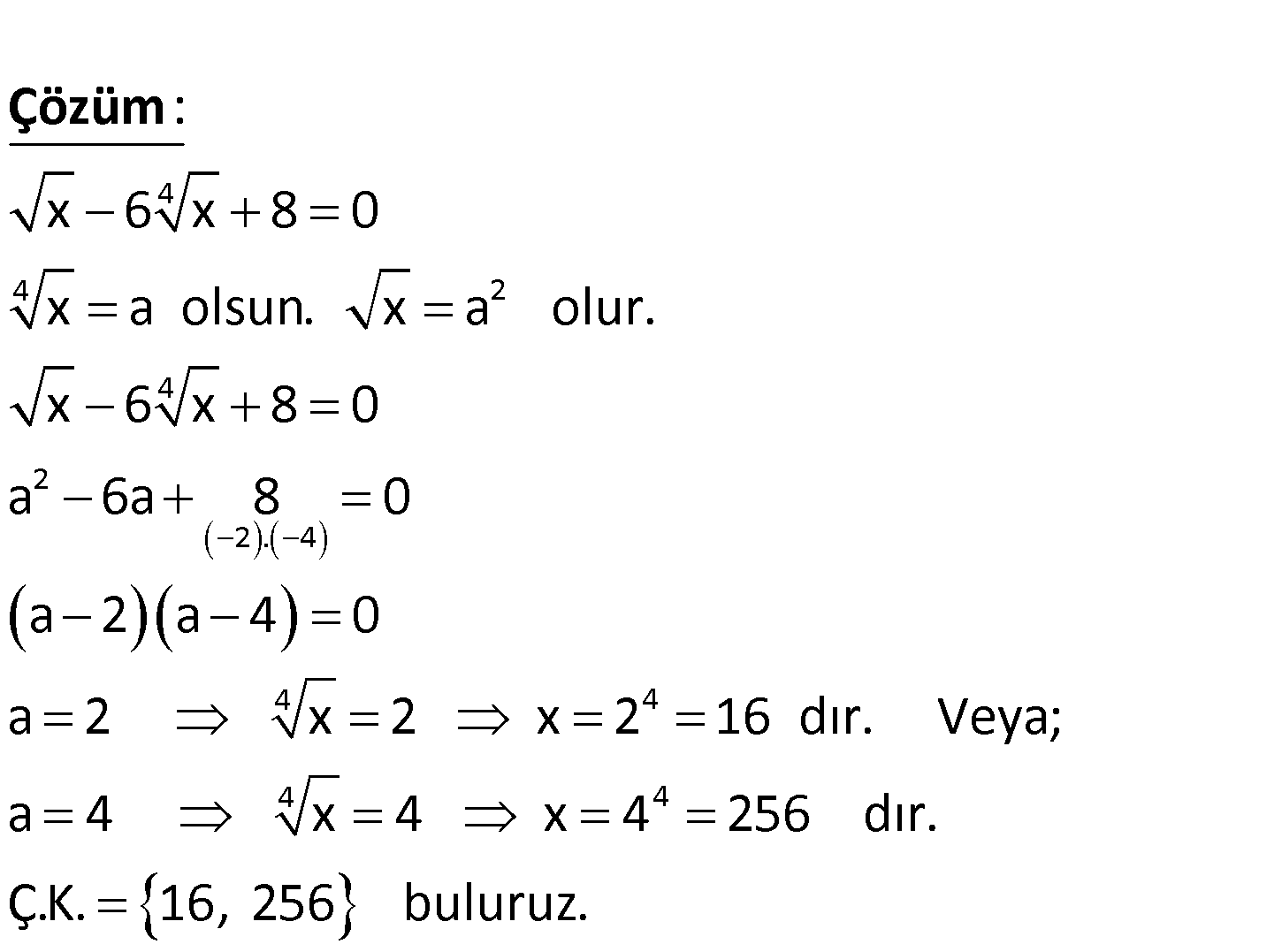
6.SORU

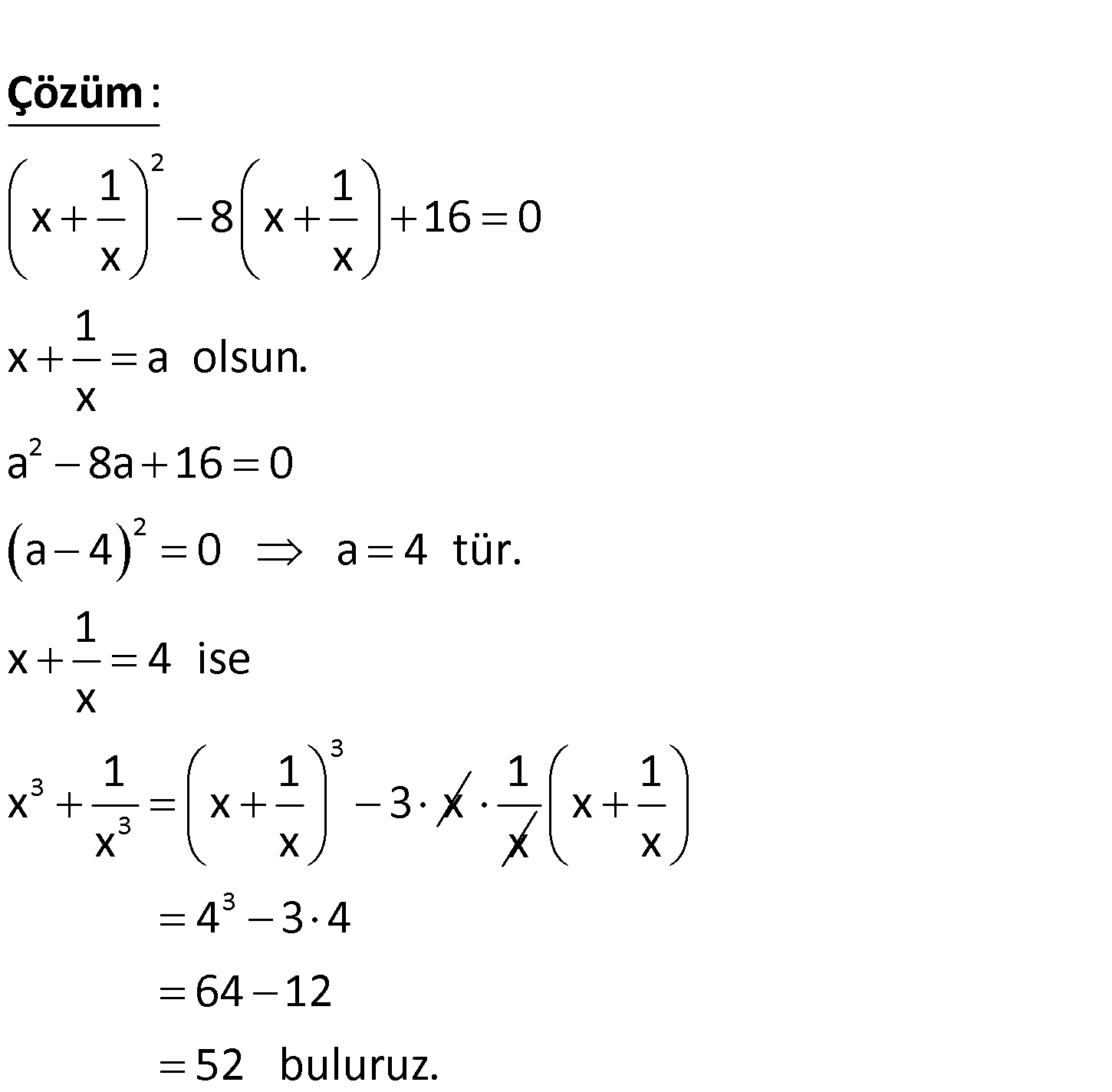
7.SORU
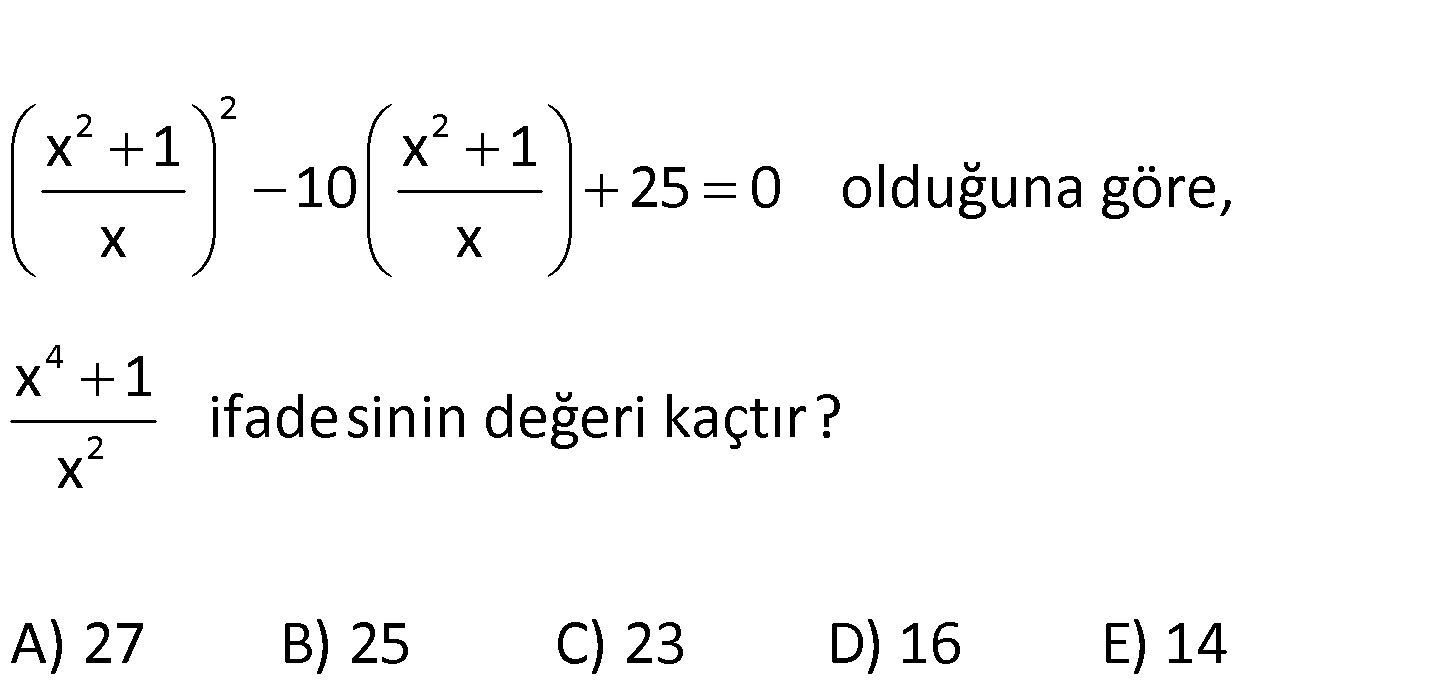
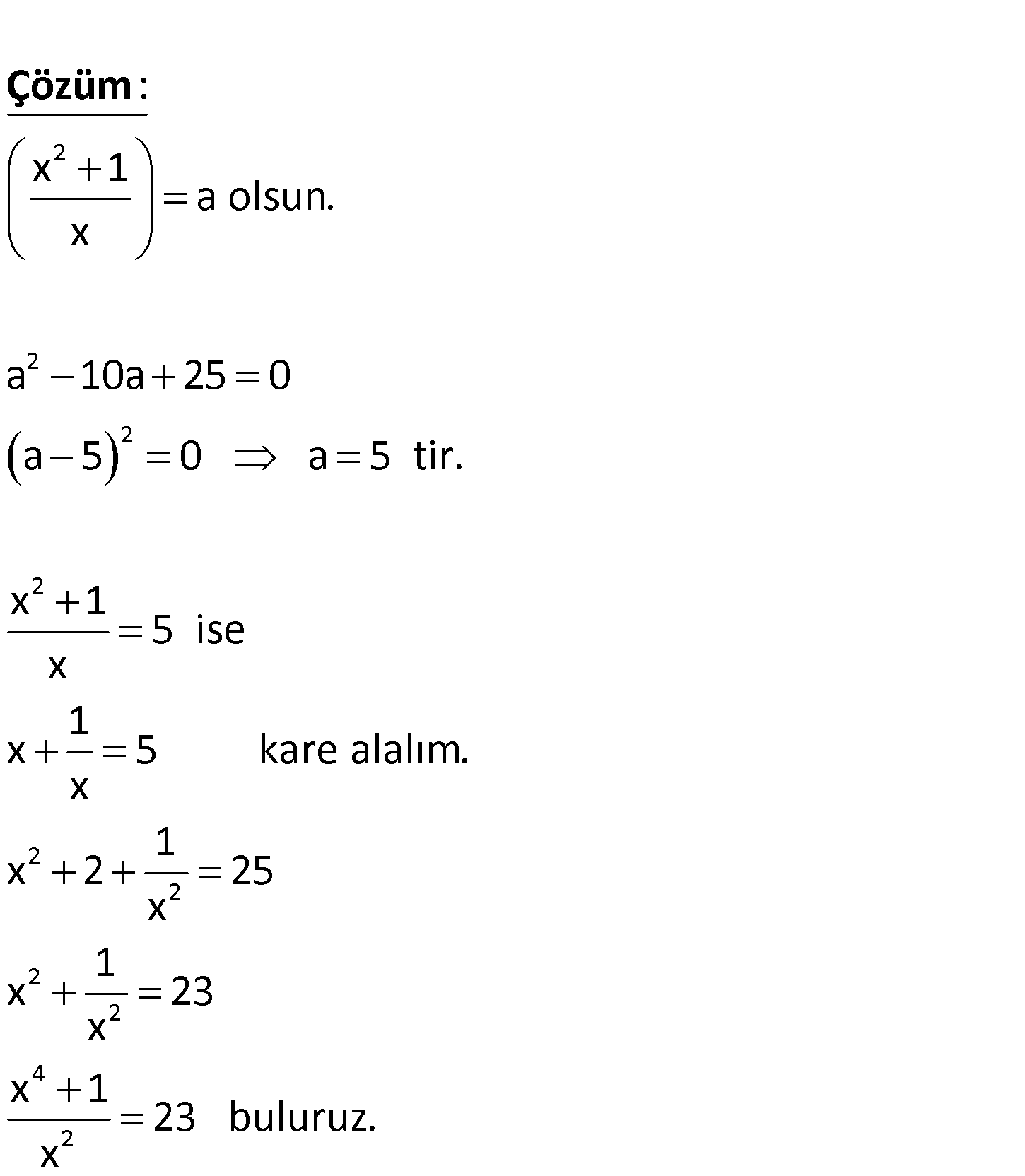
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 2 Aşağıdakilerden hangisi a 3a . a 3a 8 20 ifadesinin bir çarpanı değildir? A) a 5 B) a 2 C) a 1 D) a 1 E ) a2 2 2 2 2 x 10 x 2 2 a 5 a 2 (a 3a)(a 3a 8) 20 a 3a x olsun. x.(x 8) 20 x 8x 20 (x 10)(x 2) (a 0 : 3a 1 )( Çözüm 2 a 2 a 1 a 3a 2) (a 5)(a 2)(a 2)(a 1) dir. (a 1) çarpanı bulunmaz. 73
www.matematikkolay.net 2 2 2 a 3ab 8a 3 b ab 8b 19 olduğuna göre, a b ifadesinin pozitif değeri kaçtır? A) 4 B) 10 C) 12 D) 16 E) 20 2 2 2 2 2 a 3ab 8a 3 b ab 8b 19 Taraf tarafa toplayalım. a 2ab b 8a 8b 16 a b 8( : a Çözüm 2 2 2 2 b) 16 a b 8 a b 16 0 a b x olsun. x 8x 16 0 x 4 0 x 4 tür. a b 4 ise a b 16 buluruz. 124
2 2 x ve y reel sayılardır. x 10xy 9y 8 ve 4xy x 3y 2 ise x 3y toplamı aşağıdakilerden hangisi olabilir? A) 4 B) 3 C) 1 D) 3 E) 4 2 2 2 2 2 x 10xy 9y 8 4xy x 3y 2 taraf tarafa çıkarırsak, x 6xy 9y x 3y 6 x 3y (x 3 : Çözüm 2 2 ( 3)(2) y) 6 x 3y a diyelim a a 6 a a 6 0 (a 3)(a 2) 0 a 3 veya a 2 olabilir. Cevap: D 141
www.matematikkolay.net 2 2 2 2 2 a a 6 0 a a 4 olduğuna göre, a ifadesinin alacağı değer – a ler toplamı kaçtır? A) 15 B) 17 C) 19 D) 21 E) 23 2 2 2 2 2 a a 6 0 a a 2 2 a a 6 0 a a 2 a x olsun. a x x 6 0 x 3 x 2 0 x 3 ve x 2 : olu Çözüm 2 2 2 r. 2 2 a 3 a 3 a a a 2. a. 2 a 2 2 2 2 2 2 4 9 a 4 a 9 4 13 tür. a 2 2 a 2 a 2 a a a 2. a. 2 a 2 2 2 4 4 a 4 a 4 4 8 dir. a 13 8 21 bulunur. www.matematikkolay.net 170
4 x 6 x 8 0 çözüm kümesini bulunuz. www.matematikkolay.net 4 4 2 4 2 02.Nis 4 4 x 6 x 8 0 x a olsun. x a olur. x 6 x 8 0 a 6a 8 0 a 2 a 4 0 a 2 x 2 : x 2 1 Çözüm 4 4 6 dır. Veya; a 4 x 4 x 4 256 dır. Ç.K. 16, 256 buluruz. 191
www.matematikkolay.net 2 3 3 1 1 x 8 x 16 0 x x denklemin köklerinden biri k’dır. 1 Buna göre, k toplamı kaçtı k r? A) 42 B) 48 C) 50 D) 52 E) 56 2 2 2 3 3 1 1 x 8 x 16 0 x x 1 x a olsun. x a 8a 16 0 a 4 0 a 4 tür. 1 x 4 i x : se x 1 x x Çözüm 3 1 3 x x 1 x 3 1 x x 4 3 4 64 12 52 buluruz. 211
www.matematikkolay.net 2 2 2 4 2 x 1 x 1 10 25 0 olduğuna göre, x x x 1 ifadesinin değeri kaçtır? x A) 27 B) 25 C) 23 D) 16 E) 14 2 2 2 2 x 1 a olsun. x a 10a 25 0 a 5 0 a 5 tir. x 1 5 ise x 1 x 5 kare alalım. x x : Çözüm 2 2 2 2 4 2 1 2 25 x 1 x 23 x x 1 23 buluruz. x 222

