Soru Sor sayfası kullanılarak Belirsiz İntegral konusu altında Kısmi integrasyon (uv – S vdu) ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU
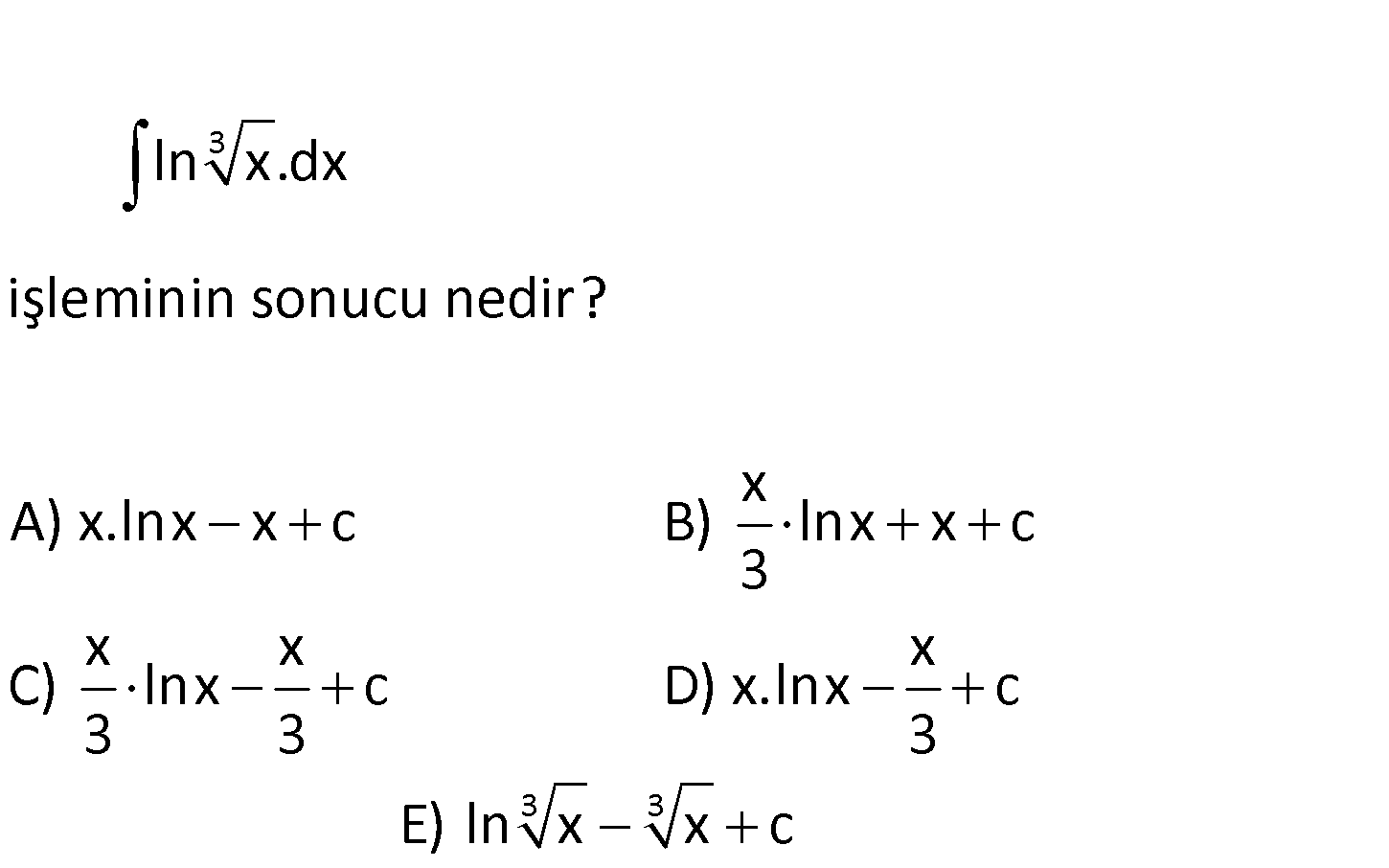
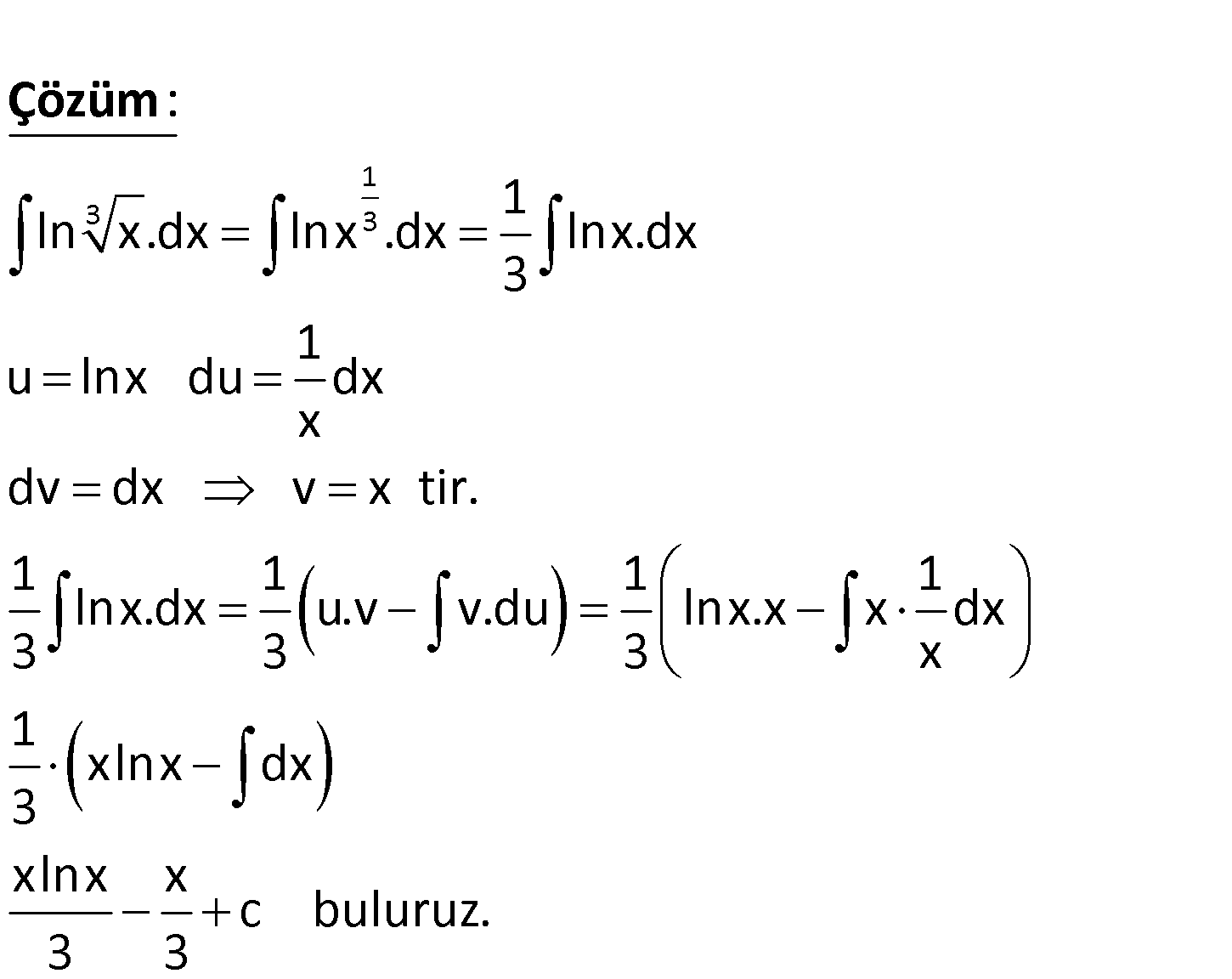
4.SORU


5.SORU
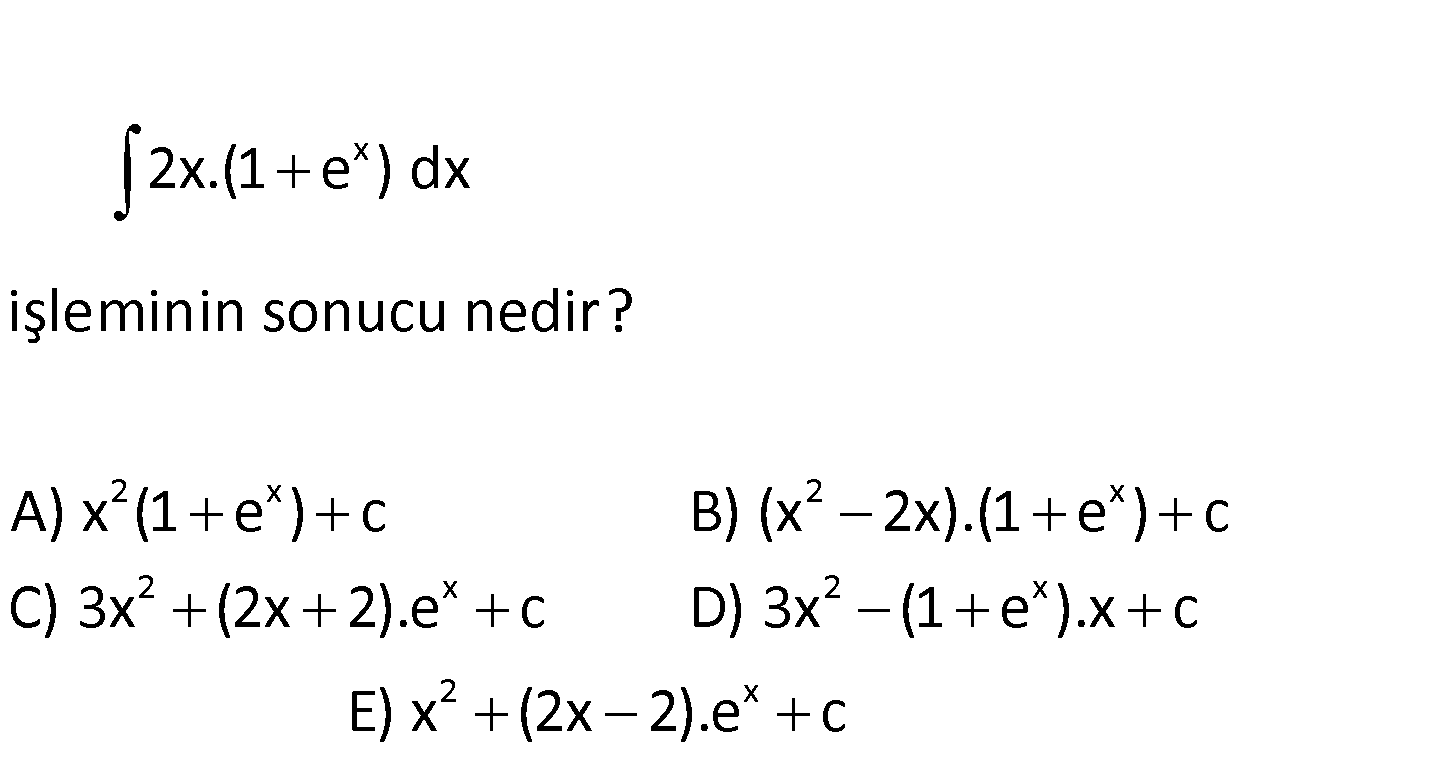
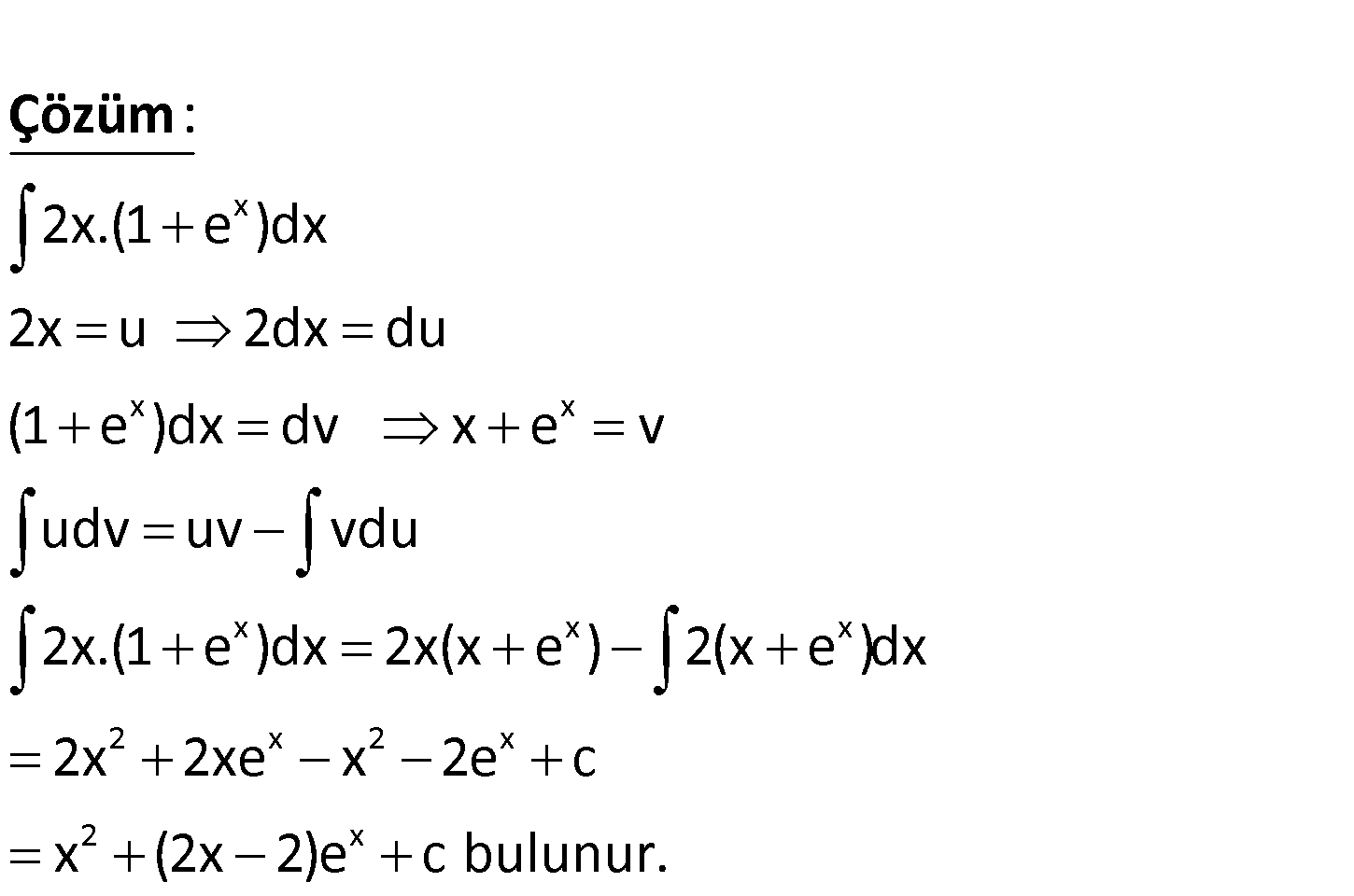
6.SORU
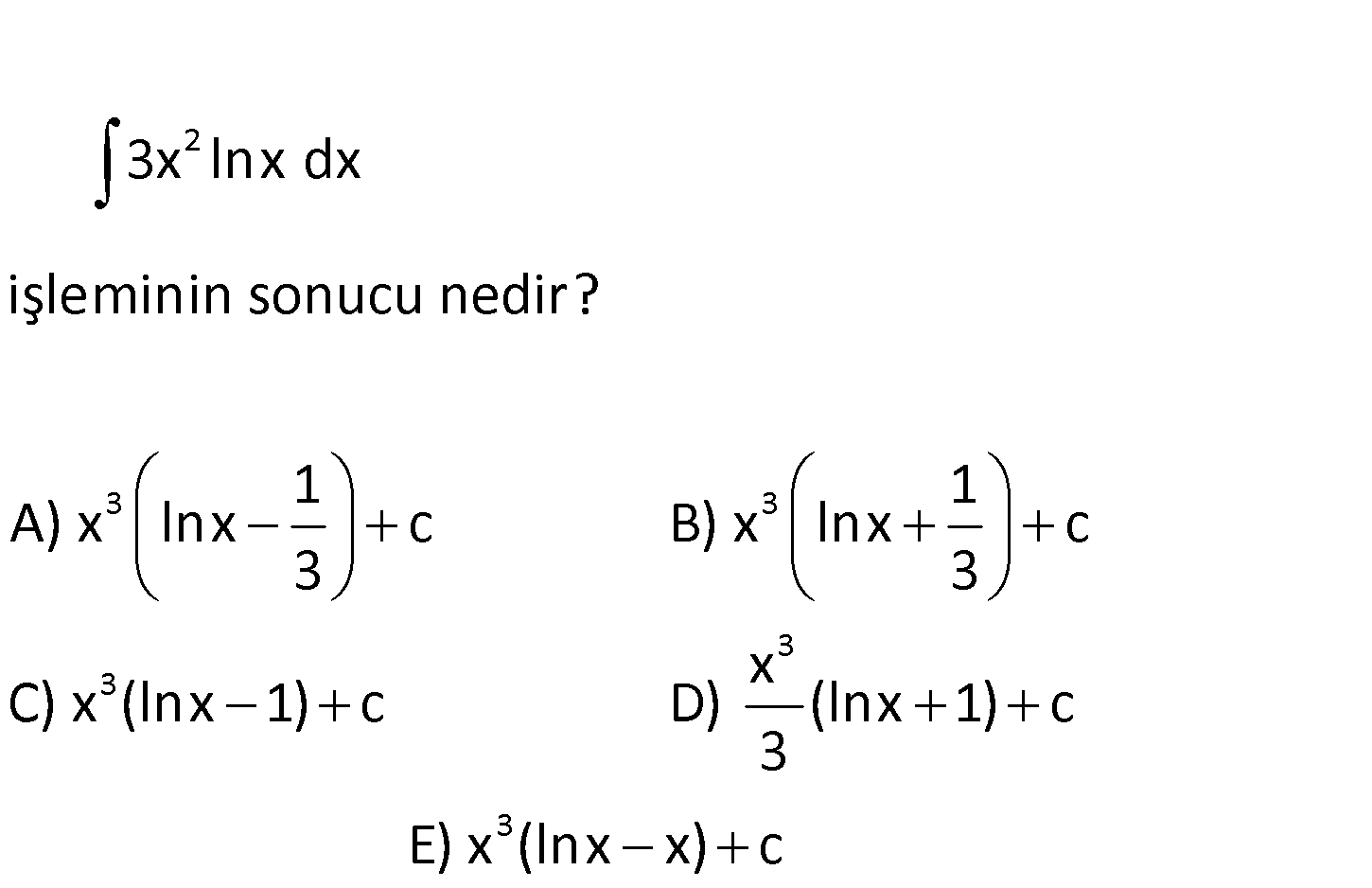
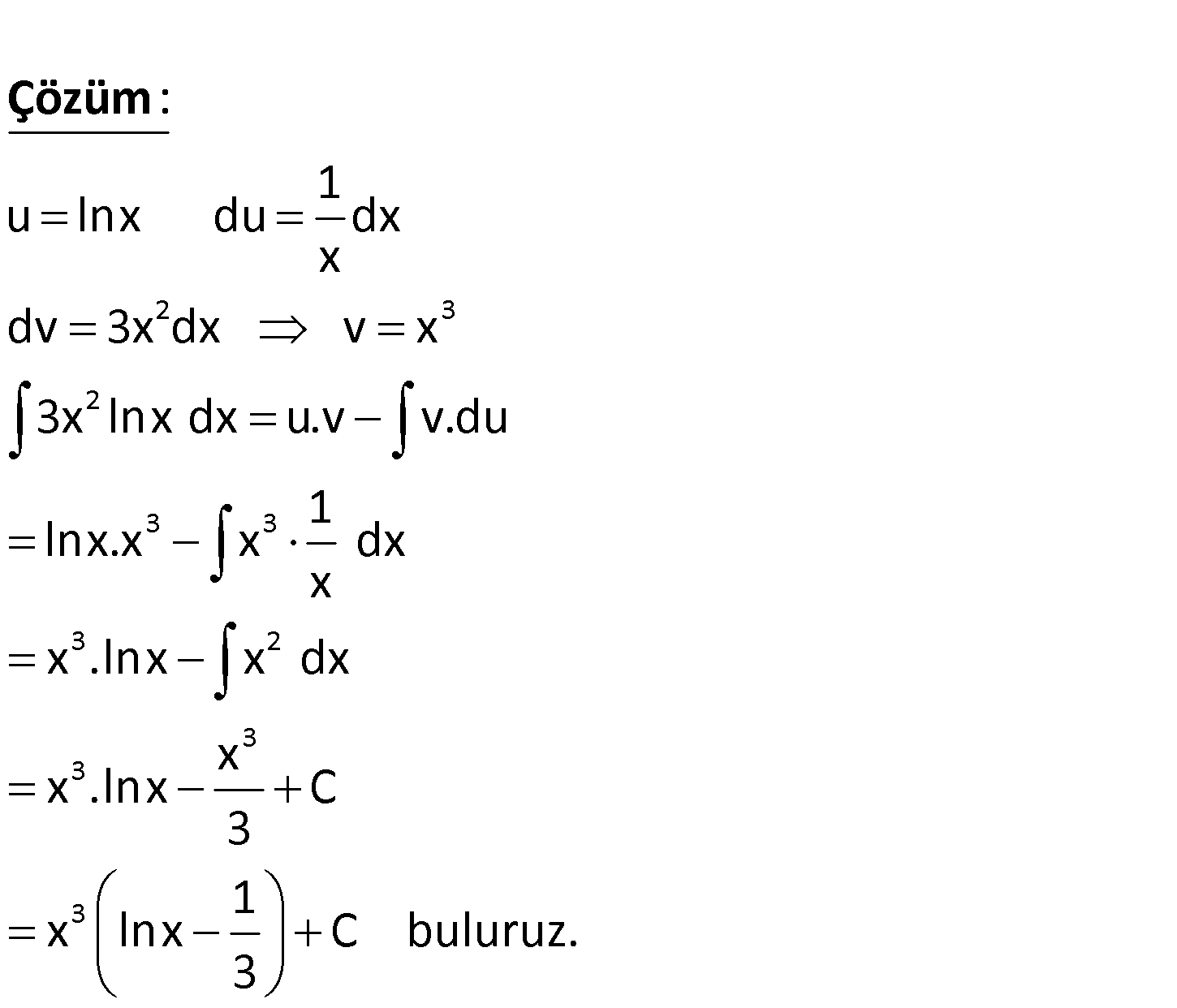
7.SORU
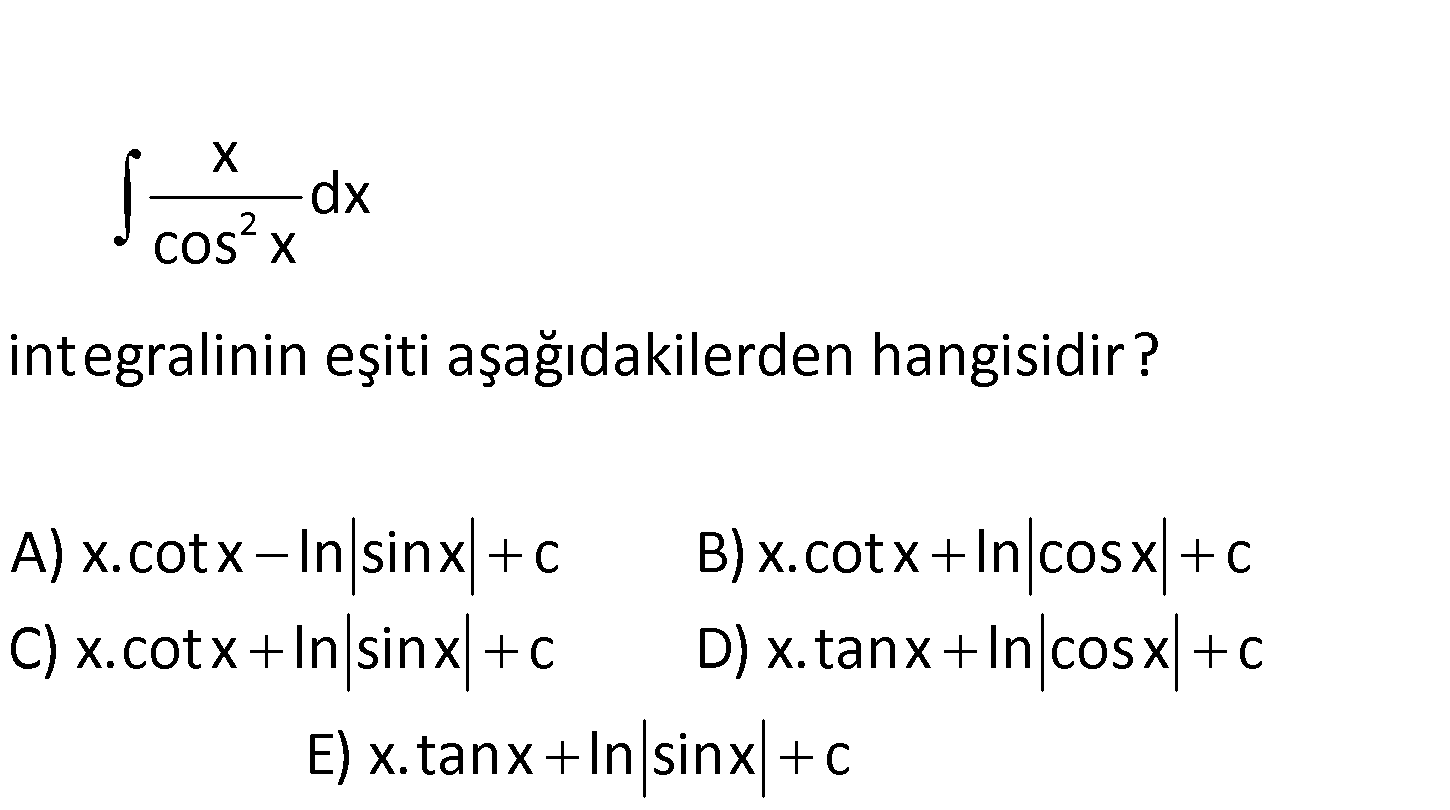
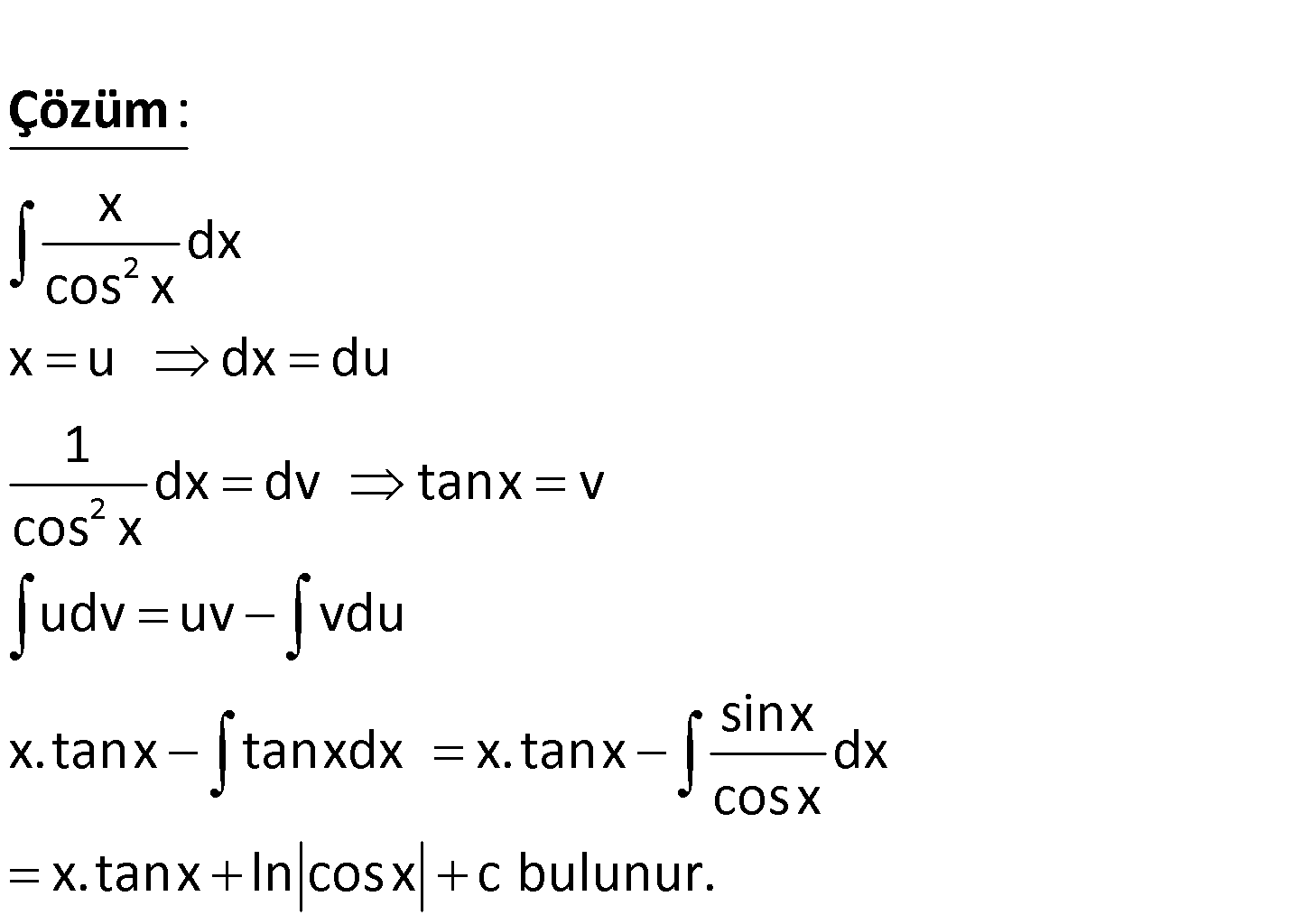
8.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 x .sinx dx ? www.matematikkolay.net 2 u dv 2 x .sinxdx Değişken değiştirelim; dv sinxdx v cosx u x d : u 2xd Çözüm 2 2 u dv 2 u dv x x .sinxdx u.v v.du x .cosx cosx.2x.dx x .cosx 2 xcosx.dx Değişken değiştirelim; dv cosxdx v sinx u x du dx 2 2 2 2 2 2 x .cosx u.v v.du x .cosx 2 x.sinx sinx.dx x .cosx 2 x.sinx ( cosx) x .cosx 2 x.sinx cosx x .cosx 2x sinx 2cosx 2x sinx (x 2).cosx C buluruz. 11
www.matematikkolay.net x x.e .dx ? x u dv x x x xe Kısmi integrasyon ile çözelim. u x du dx dv e v x u. : e e Çözüm x x x x x dv v.du x.e e .dx x.e e e (x 1) C buluruz. 18
www.matematikkolay.net 3 ln x.dx işleminin sonucu nedir? x A) x.lnx x c B) lnx x c 3 x x x C) lnx c D) x.lnx c 3 3 3 3 3 E) ln x x c 1 3 3 1 ln x.dx lnx .dx lnx.dx 3 1 u lnx du dx x dv dx v x tir. 1 1 1 lnx.dx u.v v.du lnx.x 3 3 : 3 Çözüm 1 x dx x 1 xlnx dx 3 xlnx x c buluruz. 3 3 53
www.matematikkolay.net 2 f(x) ve g(x) polinom fonksiyonlar olmak üzere x sinxdx f(x)cosx g(x)sinx olduğuna göre, f(x 2 2 2 2 2 ) g(x) aşağıdakilerden hangisine eşittir? A) x 2x B) x 2x 2 C) x 2x D) x 2x 2 E) x 2x 2 2 2 x sinxdx u x du 2xdx dv sinxd : Çözüm 2 2 2 2 x v cosx x sinxdx u.v v.du x .cosx 2 cosx.xdx u x du dx dv cosxdx v sinx x .cosx 2 cosx.xdx x .cosx 2 u. 2 2 2 2 f(x) g(x) 2 2 v v.du x .cosx 2 x.sinx sinx.dx x .cosx 2 x.sinx cosx x .cosx 2x.sinx 2cosx ( x 2)cosx 2x sinx f(x) g(x) x 2 2x x 2x 2 buluruz. www.matematikkolay.net 54
x 2 x 2 x 2 x 2x.(1 e ) dx işleminin sonucu nedir? A) x (1 e ) c B) (x 2x).(1 e ) c C) 3x (2x 2).e c D) 3x 2 x 2 x (1 e ).x c E) x (2x 2).e c www.matematikkolay.net x x x x x x 2 2x.(1 e )dx 2x u 2dx du (1 e )dx dv x e v udv uv vdu 2x.(1 e )dx : 2x(x e ) 2(x e )dx 2x Çözüm x 2 x 2 x 2xe x 2e c x (2x 2)e c bulunur. 63
www.matematikkolay.net 2 3 3 3 3 3x lnx dx işleminin sonucu nedir? 1 1 A) x lnx c B) x lnx c 3 3 x C) x (lnx 1) c D) ( 3 3 lnx 1) c E) x (lnx x) c 2 3 2 3 3 3 2 3 1 u lnx du dx x dv 3x dx v x 3x lnx dx u.v v.du 1 lnx.x x dx x x .lnx x dx x . : Çözüm 3 3 x lnx C 3 1 x lnx C buluruz. 3 www.matematikkolay.net 79
www.matematikkolay.net 2 x dx cos x integralinin eşiti aşağıdakilerden hangisidir? A) x.cotx ln sinx c B) x.cotx ln cosx c C) x.cotx ln sinx c D) x. tanx ln cosx c E) x.tanx ln sinx c 2 2 x dx cos x x u dx du 1 dx dv tanx v cos x udv uv vdu sinx x. tanx tanxdx x. tanx dx cosx x. tanx : Çözüm ln cosx c bulunur. 89
xcosx.dx ? www.matematikkolay.net xcosxdx Kısmi integrasyon ile çözelim. udv uv vdu x u dx du cosxdx dv sinx v dir. xcosxdx x : . Çözüm sinx sinxdx x.sinx cosx c bulunur 143

