Soru Sor sayfası kullanılarak Belirsiz İntegral konusu altında İntegralin içinde bölmenin türevi, İntegralin içinde çarpmanın türevi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
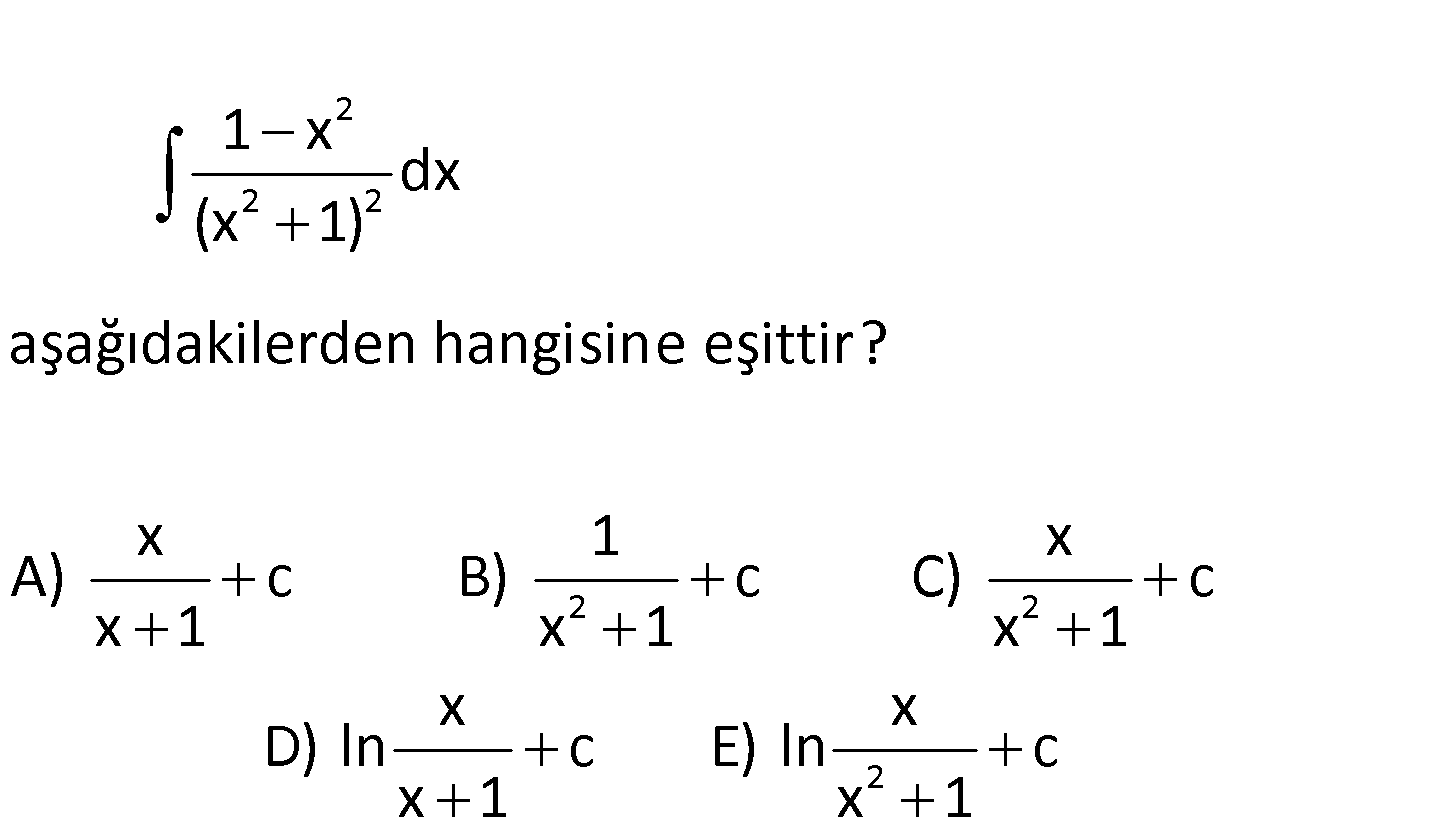
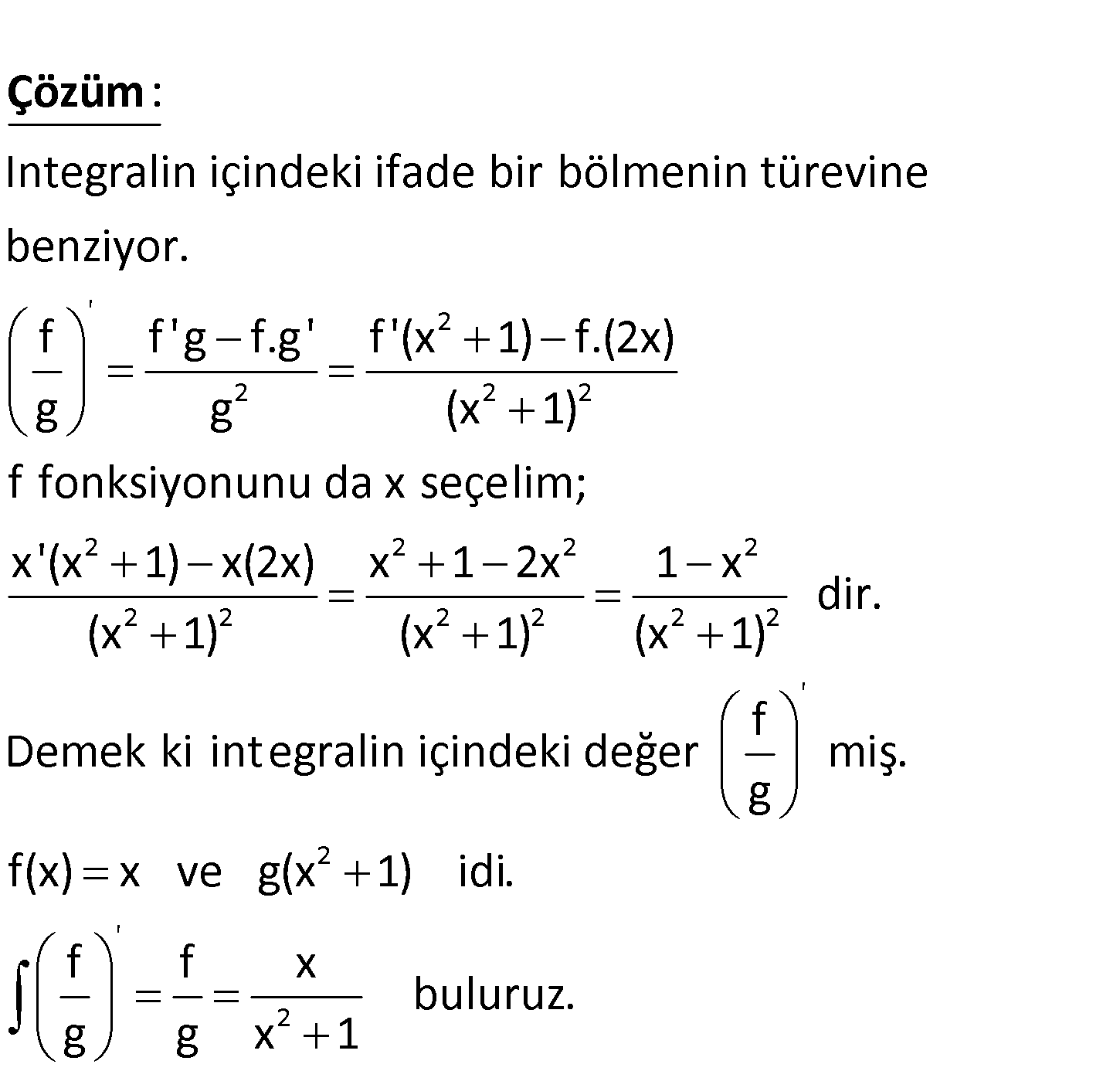
2.SORU
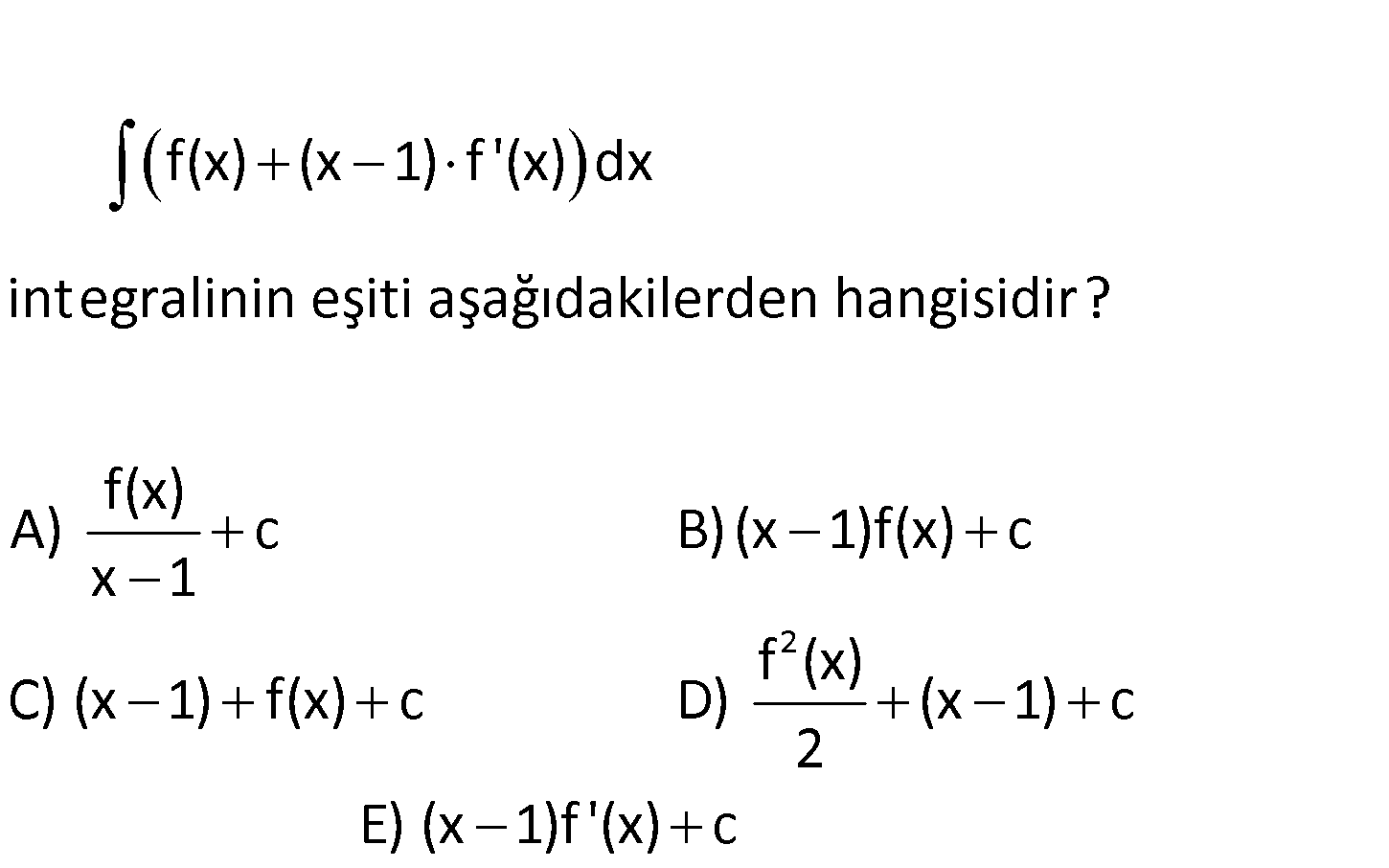
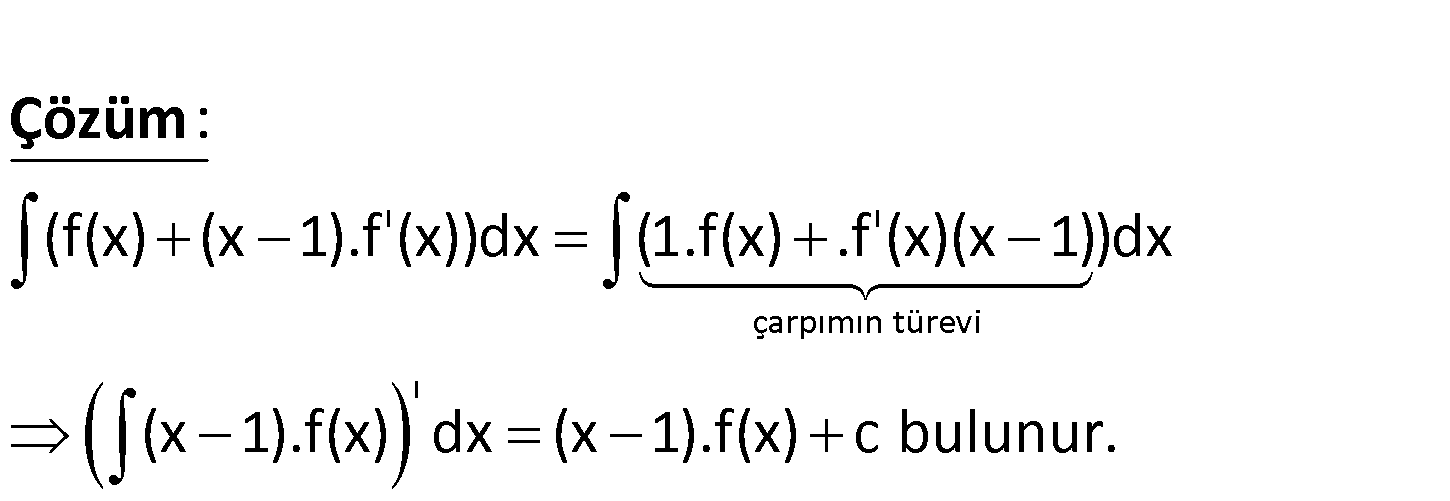
3.SORU
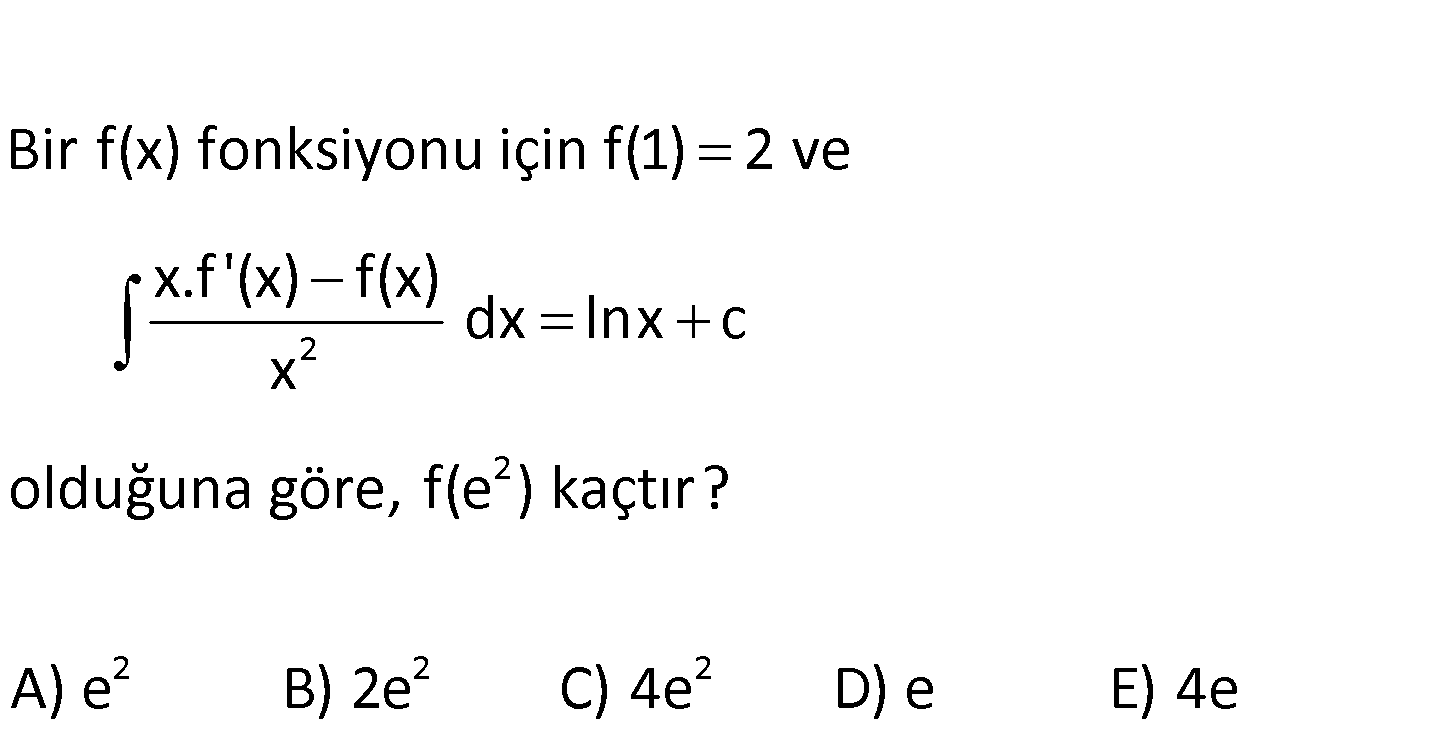

4.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 2 2 2 2 1 x dx (x 1) aşağıdakilerden hangisine eşittir? x 1 x A) c B) c C) c x 1 x 1 x 1 2 x x D) ln c E) ln c x 1 x 1 ‘ 2 2 Integralin içindeki ifade bir bölmenin türevine benziyor. f f ‘g f.g’ f ‘(x 1) f.(2x g : g Çözüm 2 2 2 2 2 2 2 2 2 2 2 2 ‘ 2 ‘ 2 ) (x 1) f fonksiyonunu da x seçelim; x'(x 1) x(2x) x 1 2x 1 x dir. (x 1) (x 1) (x 1) f Demek ki integralin içindeki değer miş. g f(x) x ve g(x 1) idi. f f x buluruz g g x 1 . www.matematikkolay.net 23
f(x) (x 1) f ‘(x) dx integralinin eşiti aşağıdakilerden hangisidir? f(x) A) c B) (x 1)f(x) c x 1 2 f (x) C) (x 1) f(x) c D) (x 1) c 2 E) (x 1)f ‘(x) c ı ı çarpımın türevi ı (f(x) (x 1).f (x))dx (1.f(x) .f (x)(x 1))dx (x 1).f(x) dx (x .f : 1) Çözüm (x)c bulunur. 87
www.matematikkolay.net 2 2 2 Bir f(x) fonksiyonu için f(1) 2 ve x.f ‘(x) f(x) dx lnx c x olduğuna göre, f(e ) kaçtır? A) e 2 2 B) 2e C) 4e D) e E) 4e 2 2 f(x) f ‘(x).x f(x) ‘in türevi dir. Bölümün türevi x x O halde; f ‘(x).x f(x) f(x) dx d di x x : Çözüm 0 2 2 2 2 2 r. c yazmadık, sorudaki c ile karışmasın diye f(x) d lnx c ise x f(x) lnx c d x f(x) x lnx c d f(1) 1. ln1 c d 2 c d 2 dir. f(e ) e lne 2 e 2 2 4e buluruz. 103
www.matematikkolay.net 6 f(0) 5, f(6) 8 ve g(x) f(lnx) f ‘(lnx) .dx olduğuna göre, g(1) g(e ) nın değeri kaçtır? (İ 6 8 8 8 6 6 ntegral sabiti 0 kabul edilecek.) A) 5e 6e B) 5 6e C) 6 5e D) 5 8e E) 5 6e f lnx f ‘ lnx dx İntegralin içinde, çarpım şeklinde yazılmış bir ifadenin türev : i var. Çözüm 0 mış. 6 6 6 6 6 6 x.f lnx in türevi Bu sebeple; f lnx f ‘ lnx dx x.f lnx c dir. g 1 g e 1.f ln1 e .f lne 1.f 0 e .f 6 1.5 e .8 5 8e buluruz. 132

