Ardışık Sayılarla ilgili problemler

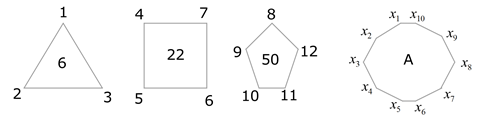
www.matematikkolay.net 1 2 3 4 5 6 7 8 Bir çocuk sırasıyla şekilde görülen tüm torbalara, torbaların üzerinde yazan numara kadar bilye atı – yor. Örneğin 4 numaralı torbaya 4 tane bilye atıyor. Çocuk yanlışlıkla bu torbalardan ikisine iki defa üzerinde yazan numara kadar bilye atmıştır. Buna göre, toplam bilye sayısı kaç farklı değer alabilir? Hangi iki torbaya 2 : kere atılmışs a toplam bilye sayısı o kada r fazla olacaktır. Örne ği n, 2 ile 5’inc i torbalar Çözüm a fazla atılmışsa toplam bilye sayısı 7 fazla olacaktır. Bu fazlalığın en az ve en çok durumlarını bulalım. En az 1 ve 2.torbalara atılınca 3 fazla olur. En çok 7 ve 8. torbalar 15 fazla 3 ile 15 dahil     aradaki tüm değerler geçerlidir. 15 3 Terim sayısı 1 12 1 13 buluruz. 1       16 www.matematikkolay.net Ceren, bölümleri sırasıyla oynanan ve kırk bölümden oluşan bir bilg isayar oyununun her bölümünü, bölüa 1 mün sıra numarası a olmak üzere dakikada 43 bitiriyor. Buna göre, Ceren oyunu kaç dakikada bitiri  r? A) 22 B) 20 C) 19 D) 18 E) 17 1 1 2 1.bölümü dakidada bitirir. 4 : 3 43 3 4 2. bölümü ise , 3. bölümü ise daki kada bi – 43 43 tirir. 40. bölümü de   Çözüm 41 dakikada bitirir. 43 Bu süreleri toplarsak, 2 3 4 41 2 3 4 … 41 … 43 43 43 43 43 1’den 41’e kadar olan sayıların toplamı 41.42 41. 42 1 2 3 …41 2               21 2 861 dir. Bu toplamdan 1 çıkarırsak; 2’den 41’e kadar olan sayıların toplamını buluruz. 860 2 3 4 … 41 860 Buna göre; 43        20 43  20 buluruz. www.matematikkolay.net 19 Birbirinden farklı n tane iki basamaklı ardışık tek doğal sayının toplamı 200 ile 270 arasındadır. Buna göre n’in alabileceği en büyük değer ile en küçük değerin toplamı kaçtır? www.matematikkolay.net : n’yi en küçük yapmak için, en büyük iki basamaklı tek sayıları seçelim. 99  97 196  200’u geçemedi. Demek ki n  Çözüm 2 2 2 2 2 olamaz. Ama n 3 olur. Örneğin; 99 97 11 n’yi en büyük yapmak için ise, en küçük iki basamaklı tek sayıları tercih edelim. 11 13 15 …..2n 1 (1 3 …. 2n 1) (1 3 … 9) n 5 n 25 tir. n 25 270                       2 n’in toplamları 3 17 20 buluruz. n 295 n 17 olur (en fazla).         37 Şekildeki karelerde birer sayı bulunuyor. Karelerde – ki her bir sayının bir önceki karede bulunan sayı ile farkları arasındaki fark 2 olduğuna göre, y m top – lamı kaçtır? A) 48 B) 50 C) 58 D) 60 E) 64  x ile 15 arasında : ki fark 15 x tir. Buna 2 ekle rsek 17 x olur. y ile 15 arasındaki fark 17 x ise; y 15 17        Çözüm x 32 x tir. Bu şekilde devam edersek; z 51 2x (19 x eklendi) m 62 3x (21 x eklendi) 55 85 4x (23 x eklendi) Burayı çözersek; 30 4x x 7,5 tur. O halde; y m 32 x 62 3x                      94 4x 94 30 64 buluruz.      48 www.matematikkolay.net A {x : 120 k x, x N} A kümesinin 6 ile tam bölünebilen 41 elemanı vardır. Buna göre, x’in alabileceği değerler toplamı kaçtır? A) 360 B) 366 C) 1800 D) 1900 E) 2175     : A {x :120 k x,x N} Bu aralıkta 6 ile bölünebilen en büyük sayı a olsun. a 120 1 41 6 a 120 6           Çözüm 40 a 120 240 a 360 tır. x, 360′ tan 365′ e kadar bu değerler de dahil tüm değerleri alabilir. x’in alabileceği değerler toplamı; 360 361 362 363 364 365 2175 bulunur.             50 1 den 56 ya kadar olan sayılar rastgele bir çember üzerine diziliyor. Herhagi art arda gelen 5 sayının toplamı en az K dır. K nın alabileceği en büyük değer kaçtır? www.matematikkolay.net 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 56 1 2 3 4 1 2 : x x x x x K x x x x x K x x x x x K … x x x x x K taraf tarafa toplayalım. 5 x x ..                        Çözüm   56 . x 56.K 56 5    57 56 2         .K May.57 K 2 142,5 K K en fazla 142 olabilir.   53 www.matematikkolay.net Ömer 94 den başlayarak ileriye doğru dörder ritmik Barış da 410 dan başlayarak geriye doğru altışar ritmik saymaktadır. Ömer in ilk söylediği sayı 94, Barış’ın ilk söylediği sayı 410 dur. Buna göre, Ömer 158 sayısını söylediğinde Barış aynı sayıda ritmik sayma yaparak hangi sayıyı söyler? : Ömer 158’i söylediğinde kaç ker e sayı söylemiştir, onu bulalım. Son Sayı İlk Sayı Terim Sayısı 1 Artış Miktarı     Çözüm 158 94 64 1 1 16 1 17 dir. 4 4 Barış da 17 sayı söylemiştir. Bu 17.sayıyı bulalım. 410 x 17 1 6 410 x 16 6 96 410 x x 314 buluruz.                54 Ardışık 42 tane tek doğal sayının toplamından elde edilen sayının birler basamağındaki rakam 6 olduğuna göre, bu sayılardan en büyüğü en az kaçtır? A) 83 B) 89 C) 95 D) 99 E) 105 www.matematikkolay.net 1.sayı 42.sayı En küçük sayı A olsun. Bu sayıl : ar sırasıyla, A , A 2, A 4, A 6 , … , A 82 dir. Toplamları A A A …       Çözüm 42 tane A A 2 4 6 … 82 42A 2(1 2 3 … 41) 42A 2             41.42 2  42A 41.42 42(A 41) dir. Bu ifadenin son hanesi 6 ise; (A 41) sonu 3 ile bitebilir. A 2 verelim . Ancak A bir tek sayı, olmaz. (A 41) sonu 8 ile bitebilir. A 7 verelim . En küçük değer A 7 dir. Bu say        ıların en büyüğü ise A 82 7 82 89 buluruz.     57 1 ile başlayan 50 basamaklı bir doğal sayının herhan – gi ardışık iki basamağında oluşan sayı 12 sayısının tam katı olduğuna göre, bu sayının rakamları top – lamı kaçtır? A) 288 B) 291 C) 300 D) 324 E) 336 www.matematikkolay.net 50 basamaklı 1…….. : ……… 1 ile başlıyorsa, bundan sonra gelecek rakam 2 olmalı ki 12’nin katı ols u Çözüm 50 basamaklı 50 basamaklı 50 basamaklı n. 12…………….. 2’den sonra da 4 gelmeli ki 12’nin katı olsun. 124…………… 4′ ten sonra 8 gelmeli 1248………….. 8’den sonra 4 (84, 50 basamaklı 50 basamaklı 48 tane ( 12’nin katıdır) 12484…………. 4′ ten sonra 8, 8’den sonra 4 şeklinde sürekli devam eder. 1248484848484….84848 Rakamları toplayalım; 12 4  8  4  8 … 24’er 4 ve 8) 1 2 24(4 8) 3 24.12 291 buluruz.        61 Yukarıdaki çokgenler ile çokgenlerin köşelerindeki ve içindeki sayılar belirli bir kurala göre oluşturul – muştur. Buna göre, A kaçtır? A) 460 B) 475 C) 485 D) 500 E) 505 www.matematikkolay.net : 1 2 3 6 4 5 6 7 22 8 9 10 11 12 50 Sonraki 6 sayının toplamı= Sonraki 7 sayının toplamı= Sonraki 8 sayının toplam             Çözüm ı= Sonraki 9 sayının toplamı= Buraya kadar kulanılan sayı 3 4 5 6 7 8 9 9 3 9 3 1 7 6 42 dir. 1 2 Bundan sonraki 10 sayı 43, 44, 45, 46, 47, 48, 49, 50, 51, 52 Toplamları Terim Sayısı . Or tanca Te                        rim  10 5 43 52 2    5.95  475 buluruz. www.matematikkolay.net 85 www.matematikkolay.net Selim, bir kağıda 1 den 50 ye kadar olan doğal sayı – yıları yazıyor. Daha sonra sürekli olarak bu kağıttaki sayılardan 3 tanesini silip sildiği toplamın 8 fazlası – nı kağıda yazıyor. Selim, bu işleme kağıtta 2 tane sayı kalana kadar devam ediyor. Buna göre, kağıtta kalan son iki sayının toplamı kaçtır? A) 1464 B) 1465 C) 1466 D) 1467 E) 1468 İlk başta 50 tane : sayı var. 3 sayı seçiyor. Sonra 8 ek liyor. Bu sayıyı da kağıda yazıyor. Bu durumda kağıtta 48 Çözüm 1 den 50 ye kadar olan sayılar sayı olur. Her seferinde kağıtta 2 sayı eksiliyor. 50 sayıdan 2 sayıya kadar düşene kadar 24 kere bu işlem yapılmıştır. Yani 24 kere 8 eklenmiştir. O halde tüm toplam; 50.51 24 2  Yapılan eklemeler .8 1275192 1467 buluruz. 107