Soru Sor sayfası kullanılarak Polinomlar konusu altında Yerine yazarak kalan bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
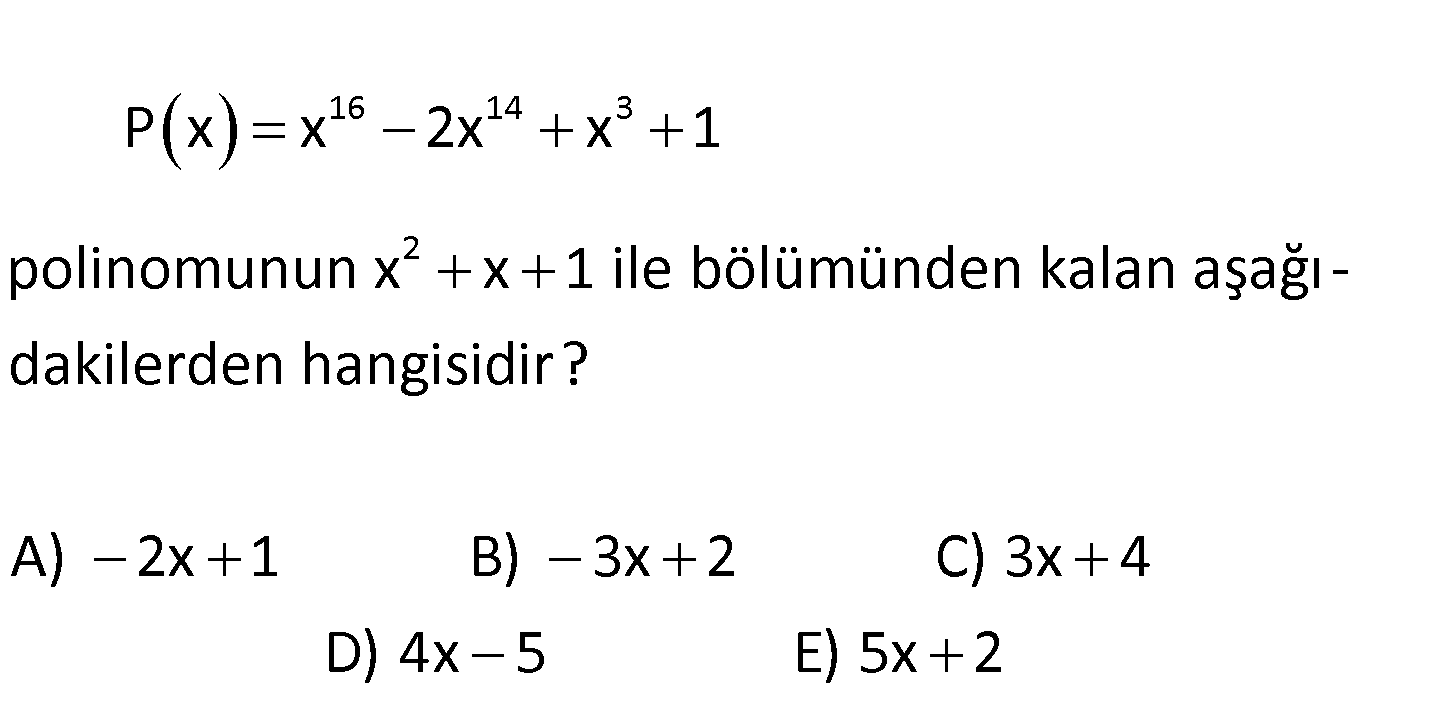

2.SORU
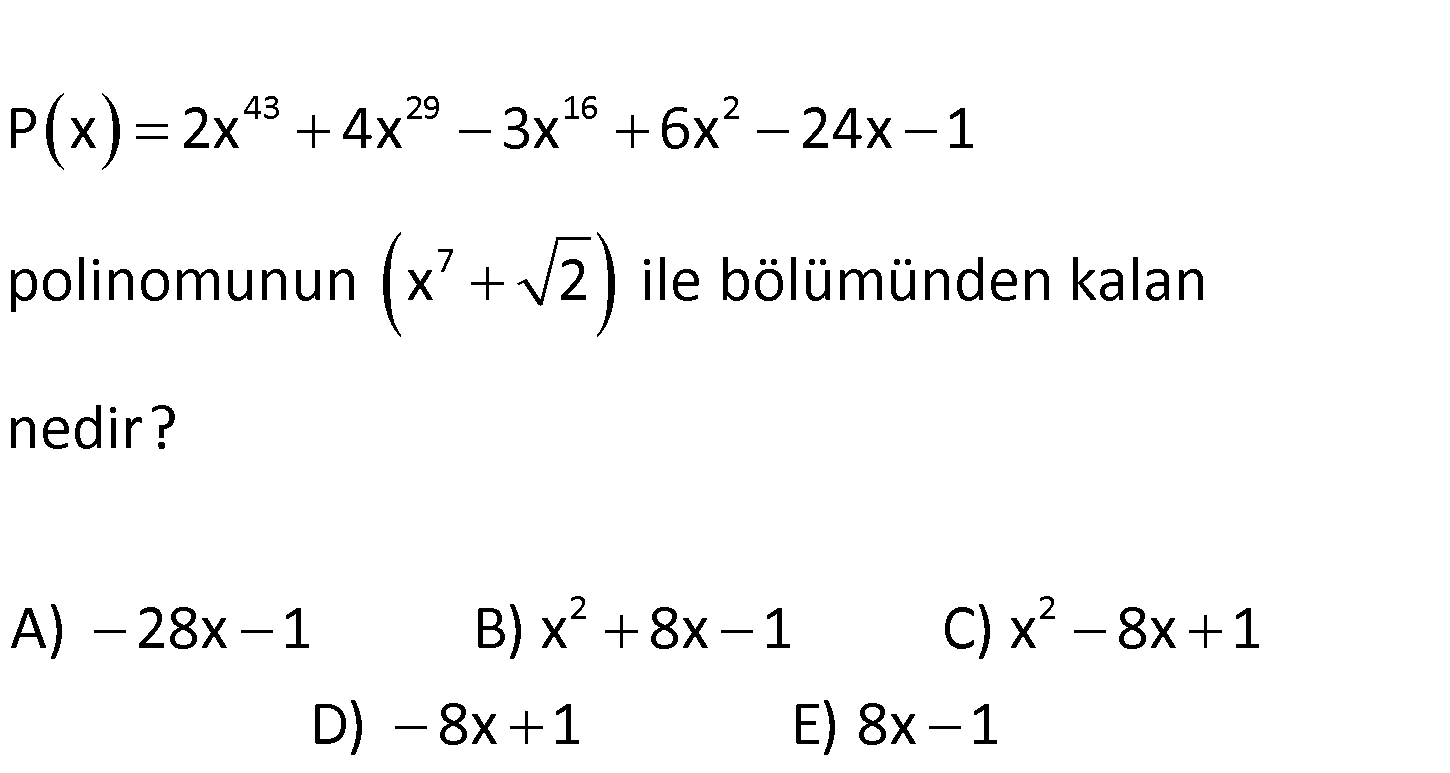

3.SORU


4.SORU


5.SORU


6.SORU
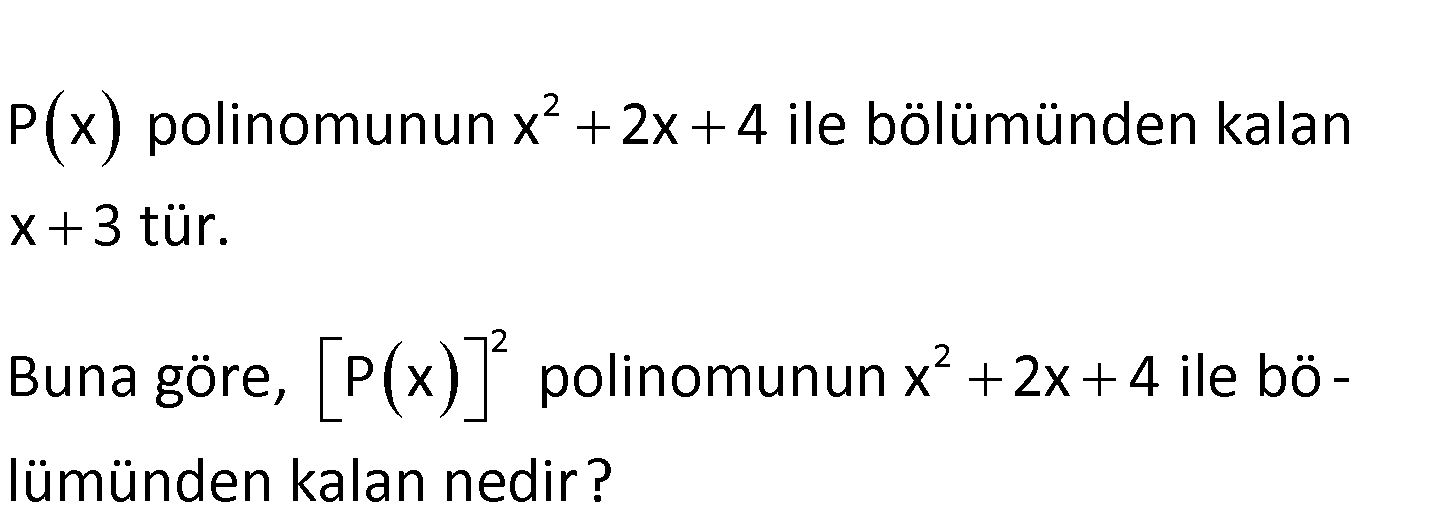

7.SORU
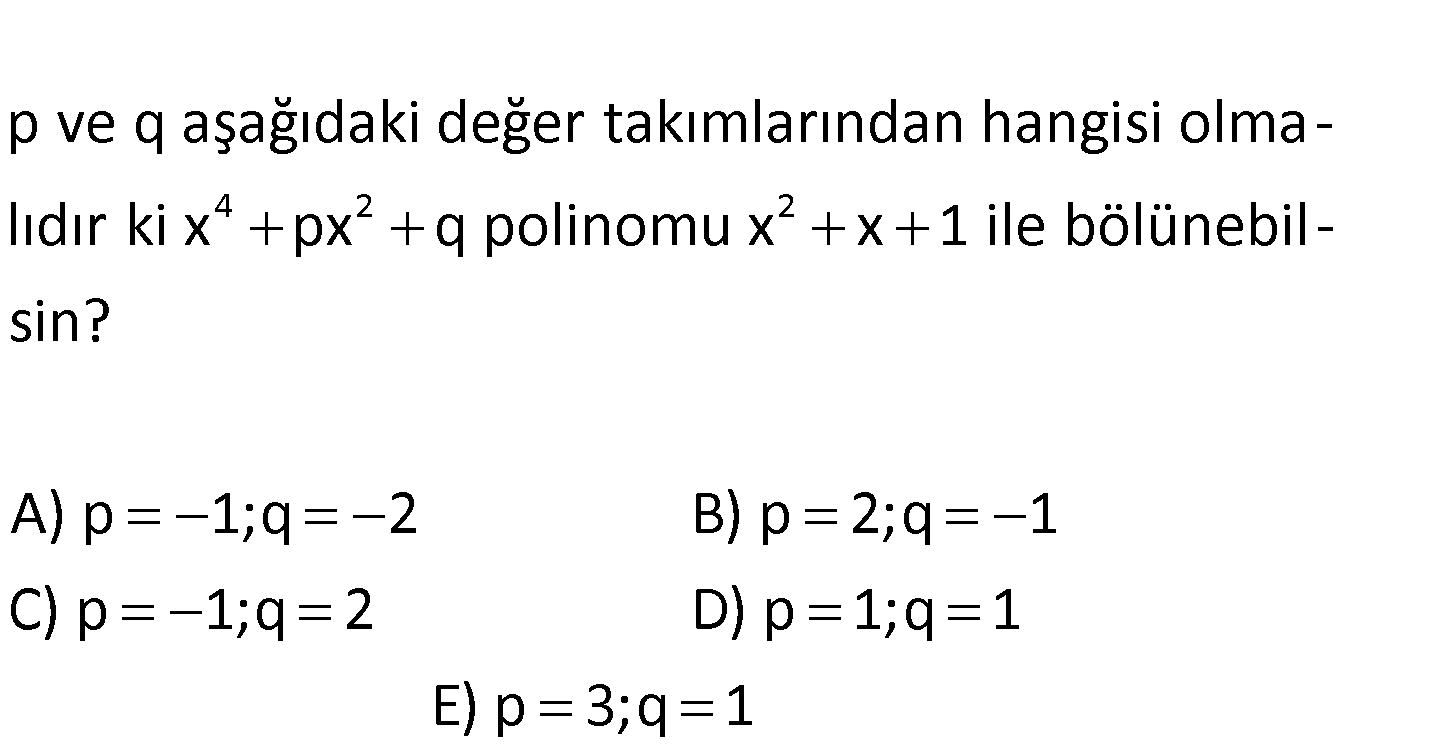

8.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 16 14 3 2 P x x 2x x 1 polinomunun x x 1 ile bölümünden kalan aşağı – dakilerden hangisidir? A) 2x 1 B) 3x 2 C) 3x 4 D) 4x 5 E) 5x 2 2 2 4 2 2 x x 1 0 a eşitleyelim. x x 1 dir. Bunun karesini alalım. : x x 2x 1 olur. x x 1 y Çözüm 4 4 3 16 14 3 3 5 3 4 2 3 3 2 2 azabiliriz. x x 1 2x 1 x x olur. x’le sadeleştirelim. x 1 dir. Bunu kullanalım. P x x 2x x 1 x .x 2 x .x x 1 x 1 yazalım. x 2x 1 1 x x 1 yazalım. x 2 x 1 2 x 2x 2 2 3x 4 bul uruz. 83
43 29 16 2 7 2 2 P x 2x 4x 3x 6x 24x 1 polinomunun x 2 ile bölümünden kalan nedir? A) 28x 1 B) x 8x 1 C) x 8x 1 D) 8x 1 E) 8x 1 www.matematikkolay.net 7 7 43 29 16 2 x 2 0’a eşitleyelim. x 2 yazarak kalanı bulabiliriz. P(x) 2x 4x 3x 6x 24x 1 P( : x) 2 Çözüm 1 42 1 28 2 14 2 1 7 6 1 7 4 2 7 2 2 6 4 2 2 2 2 2 2 2 x x 4x x 3x x 6x 24x 1 P(x) 2x (x ) 4x (x ) 3x (x ) 6x 24x 1 P(x) 2x(- 2) 4x(- 2) 3x (- 2) +6x 24x 1 P(x) 2x.8 4x.4 3x .2 6x 24x 1 P(x) 16x 16x 6x 6x 24x 1 P(x) 8x 1 buluruz. 94
www.matematikkolay.net 5 3 2 2 P x 2x 4x 2x mx n polinomunun çarpanlarından biri x 1 olduğuna göre m.n kaçtır? A) 12 B) 8 C) 10 D) 12 E) 18 2 2 2 2 P(x) polinomunun çarpanlarından biri x 1 ise P(x) polinomu x 1 ile tam bölünür. x 1 0 x : Çözüm 2 2 5 3 2 2 2 2 2 2 1 x yerine 1 yazıldığında P(x) polinomu 0’a eşit olmalıdır. Önce P(x) polinomunu x ye göre düzenleyelim. P(x) 2x 4x 2x mx n P(x) 2(x ) x 4x x 2x mx n 2( 1) x 4( 1)x 2( 1) mx n 0 2x 4x 2 mx n 0 (6 m )x n 2 0x 0 6 m 0 ve n 2 0 Buradan m 6 ve n 2 buluruz. m n 6 2 12 buluruz. Doğru Cevap : A Şıkkı 96
12 8 5 4 P x x 3x 5x 2x 1 polinomunun x 1 ile bölümünden kalan kaçtır? A) 3x 1 B) 3x 1 C) 4x 1 D) 4x 1 E) 5x 3 4 4 x 1 0 x 1 (polinomda bu değeri yerine : Çözüm 12 8 5 4 3 4 2 4 3 2 yazalım) P(x) x 3x 5x 2x 1 P(x) (x ) 3(x ) 5x .x 2x 1 1 3.1 5.1.x 2x 1 1 3 5x 2x 1 3x 1 buluruz. www.matematikkolay.net 126
www.matematikkolay.net der Q x 2 olmak üzere P x 3 x 6 .Q x 3 4x 11 olduğuna göre, P x 6 polinomunun Q x polino – mun a bölümünden kalan aşağıdakilerden hangisi – dir? A) 4x 5 B) 4x 3 C) 4x 1 D) 2x 3 E) 2x 5 P(x 3) (x 6).Q(x 3) 4x 11 x yerine x 3 yazalım. P(x 6) (x 9).Q(x) 4(x 3) 11 P(x 6) (x 9) : .Q(x) 4 Çözüm Kalan x 12 11 P(x 6) (x 9).Q(x) 4x 1 Kalan 4x 1 dir. 89
www.matematikkolay.net 2 2 2 P x polinomunun x 2x 4 ile bölümünden kalan x 3 tür. Buna göre, P x polinomunun x 2x 4 ile bö – l ümünden kalan nedir? 2 2 P(x), x 2x 4 ile bölümünden kalan (x 3) ise P(x) x 3 miş gibi işlem yapabiliriz. [P ) : (x ] (x Çözüm 2 2 2 2 Kalan 3) x 6x 9 tür. x 6x 9 1.(x 2x 4) 4x 5 Kalan 4x 5 buluruz. 90
4 2 2 p ve q aşağıdaki değer takımlarından hangisi olmalıdır ki x px q polinomu x x 1 ile bölünebil – sin? A) p 1;q 2 B) p 2;q 1 C) p 1;q 2 D) p 1;q 1 E) p 3;q 1 www.matematikkolay.net 2 2 4 2 2 2 2 2 2 x x x 1 0 x x 1 diyelim. Sonra 0’a eşitleyelim. x px q x px q x 1 p( x 1) q 0 : x Çözüm 1 2x 1 px p q 0 x 1 2x 1 0 olmalı 0 olmalı px p q 0 x px p q 0 x(1 p) p q 0 p 1 ; q 1 buluruz. 95
29 20 11 2 10 8 7 P x x x x x polinomunun x 1 x x … x 1 polinomu ile bölümünden kalan aşağıdakilerd 10 20 10 20 en hangisidir? A) 2 .x B) 2 .x C) 2 D) 2 E) 1 www.matematikkolay.net n n 1 n 2 8 7 9 9 Not : x 1 (x 1)(x x … x 1) dir. (x 1)(x x … x 1) x 1 dir. Poli : nomun x 1 ile bölüm Çözüm 9 9 29 20 11 2 10 9 3 2 10 9 2 9 2 9 2 2 3 2 2 2 2 2 10 2 10 10 20 20 9 2 2 20 2 2 20 ünden kalanı bulmak için; x 1 0 x 1 yazmalıyız. P(x) (x x x x ) polinomu x cinsinden düzenleyelim. P(x) x .x x .x x .x x 1 .x 1 .x 1.x x 4x 4 .x 2 . x .x 2 .1 .x 2 2 .x buluruz. 137

