Soru Sor sayfası kullanılarak Polinomlar konusu altında Polinomun kendisini ortaya çıkarma, polinomu bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
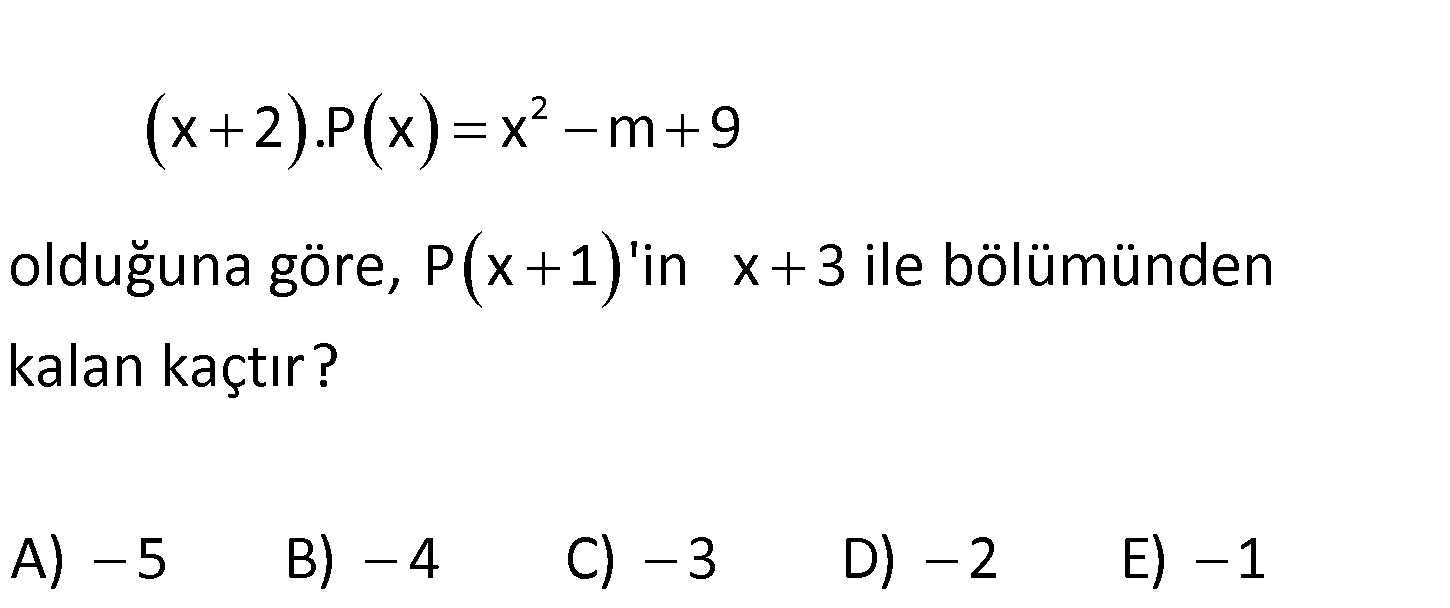

2.SORU
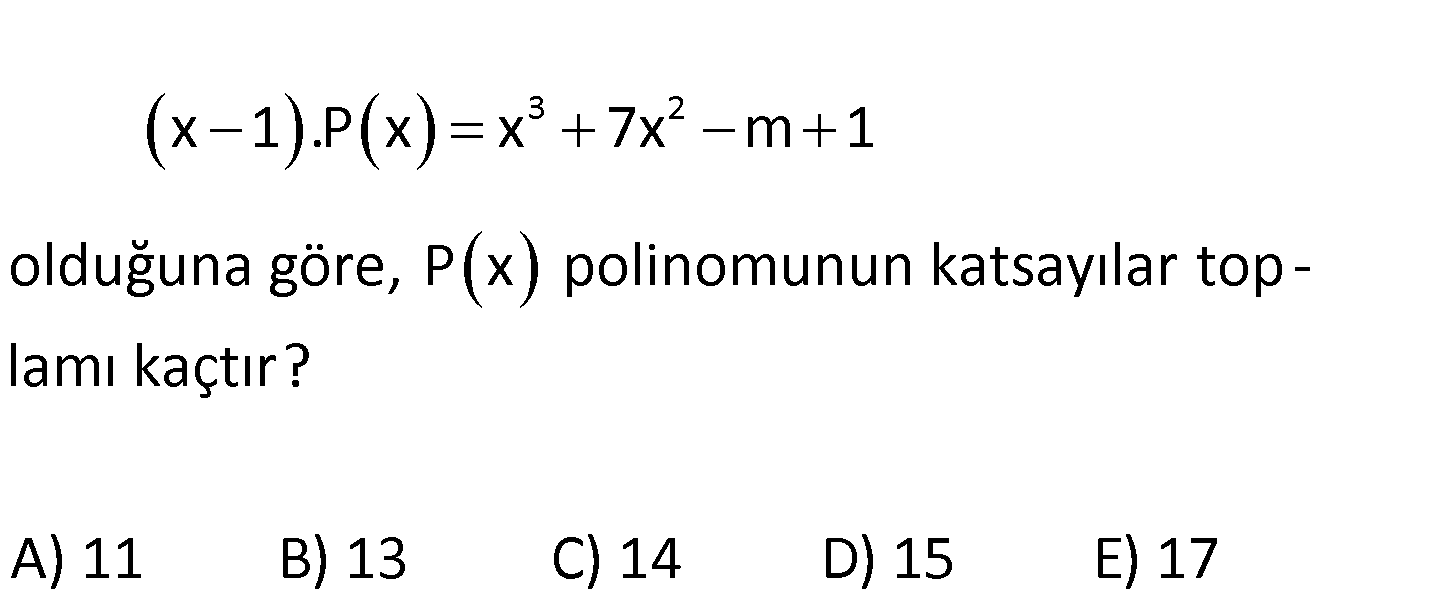

3.SORU


4.SORU


5.SORU


6.SORU


7.SORU
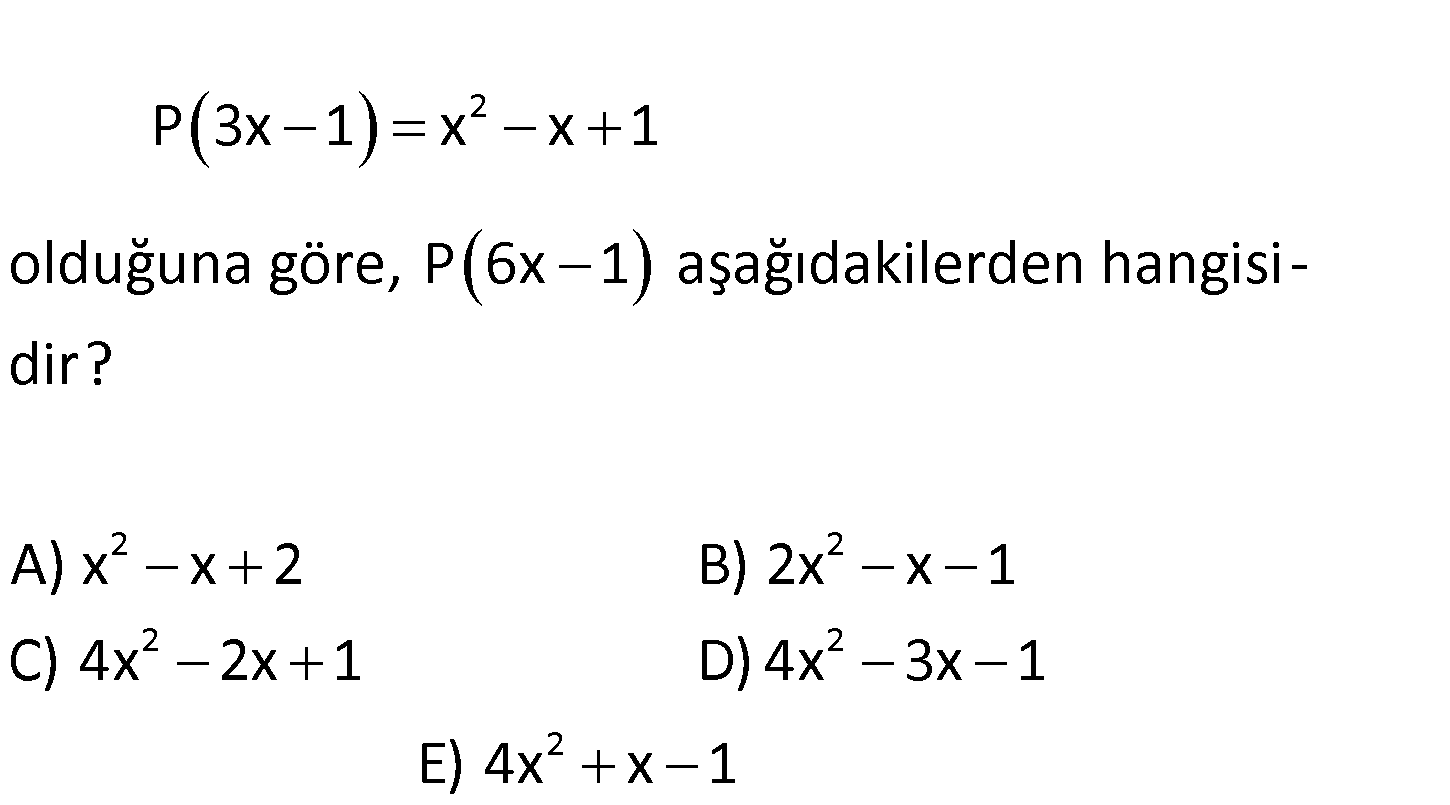
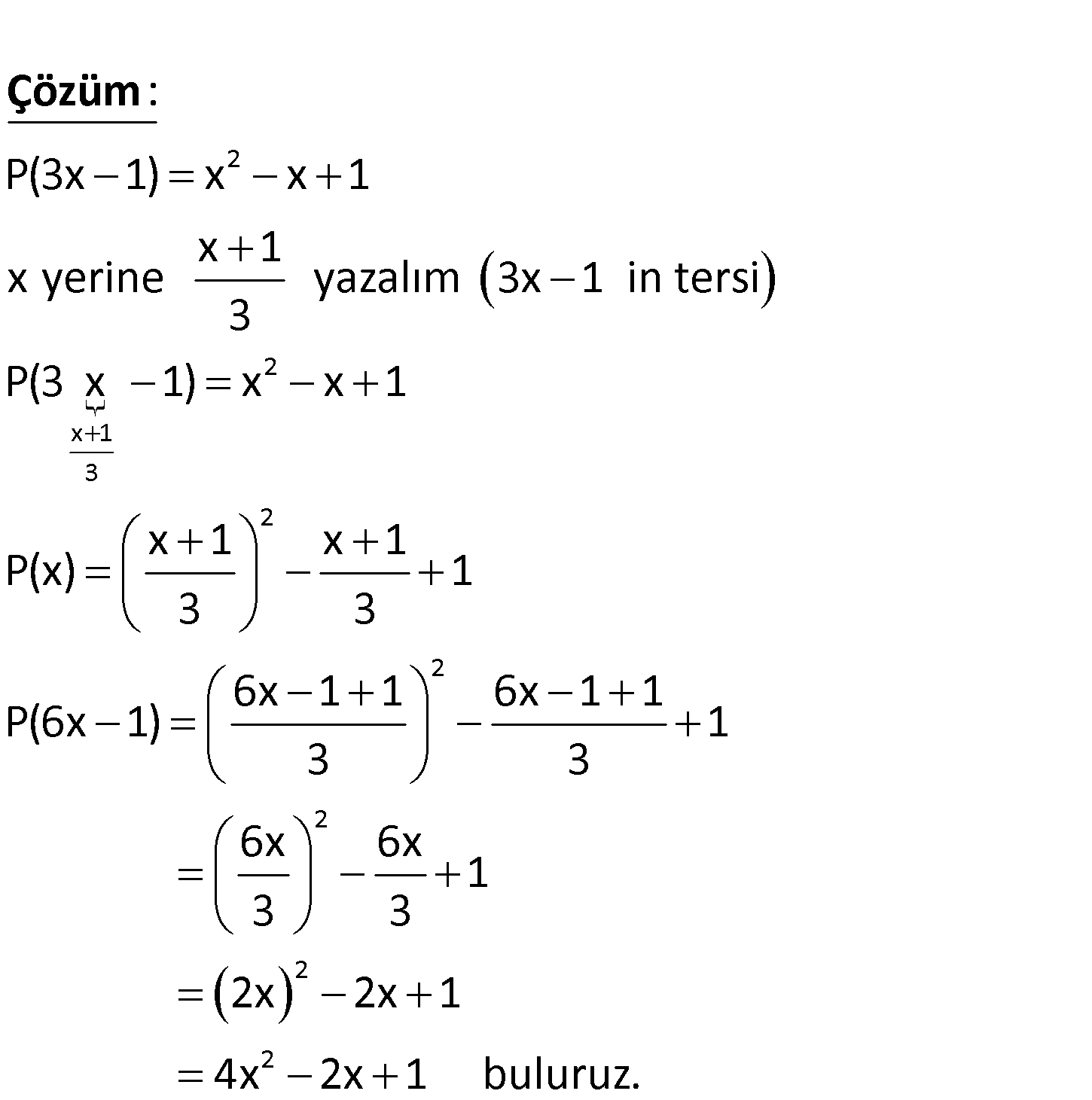
8.SORU


9.SORU
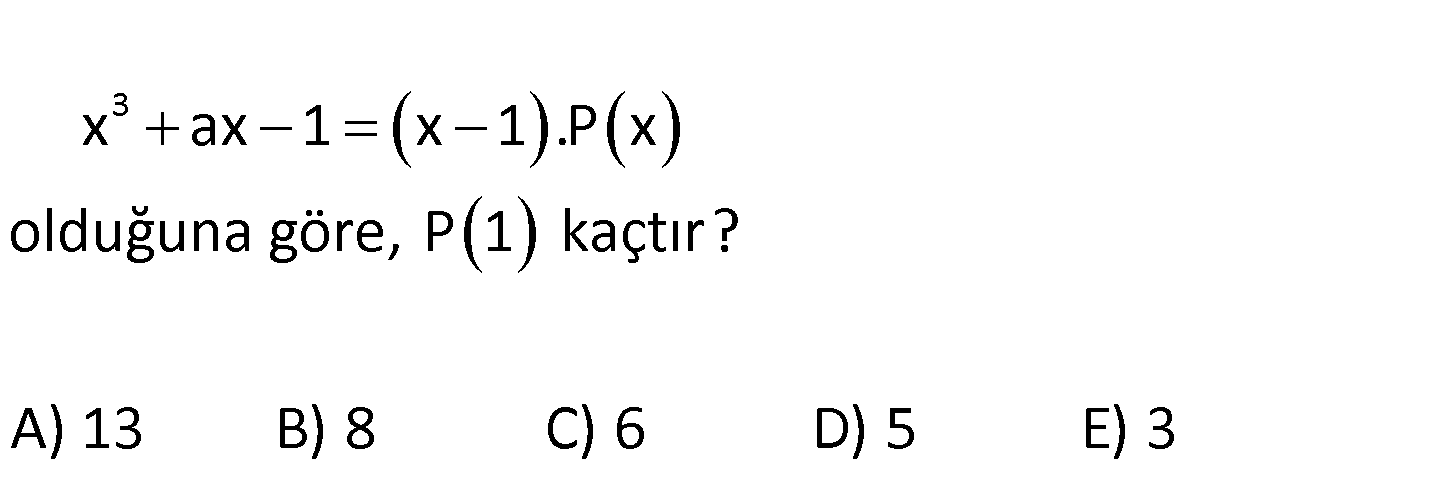

10.SORU

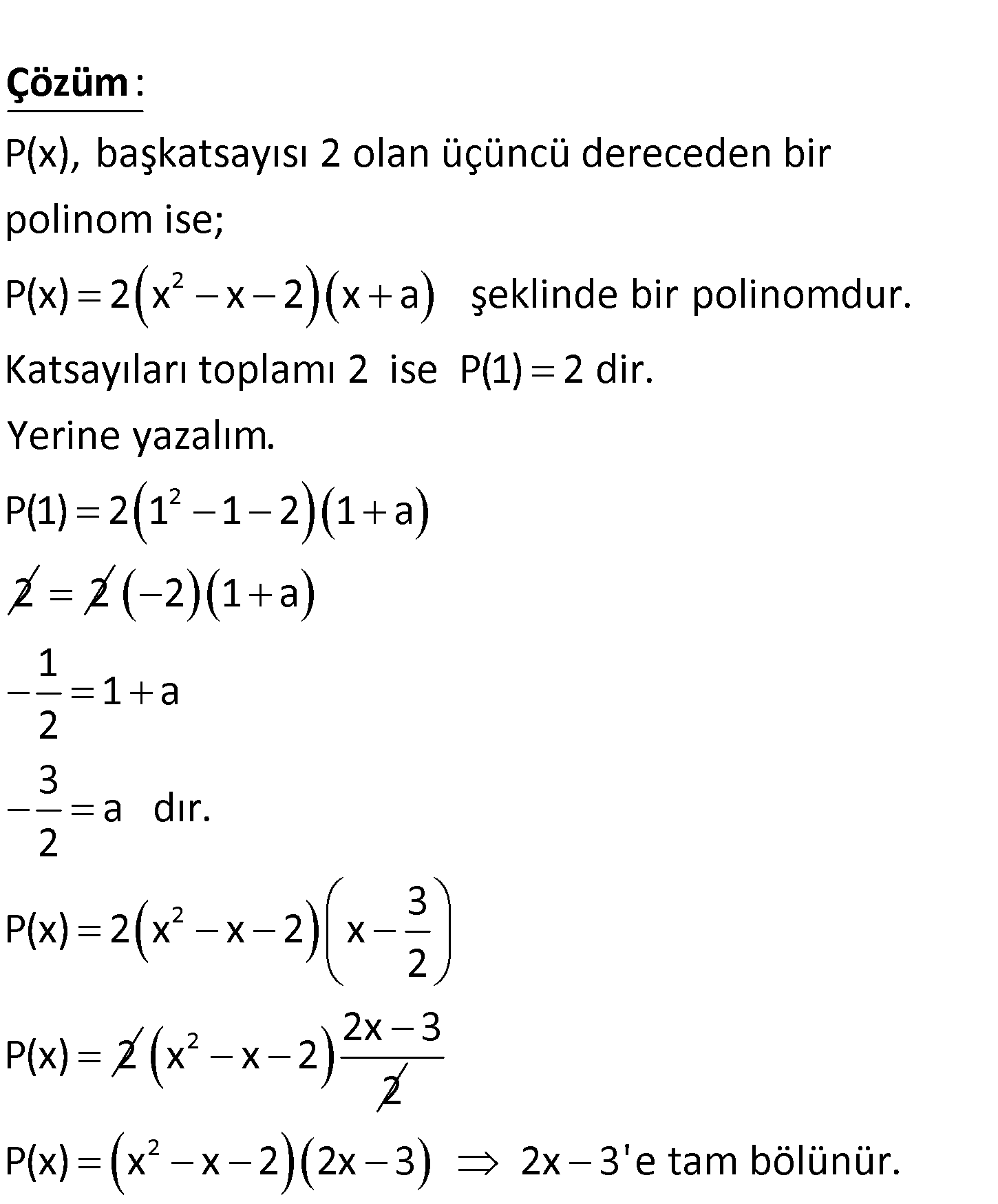
11.SORU

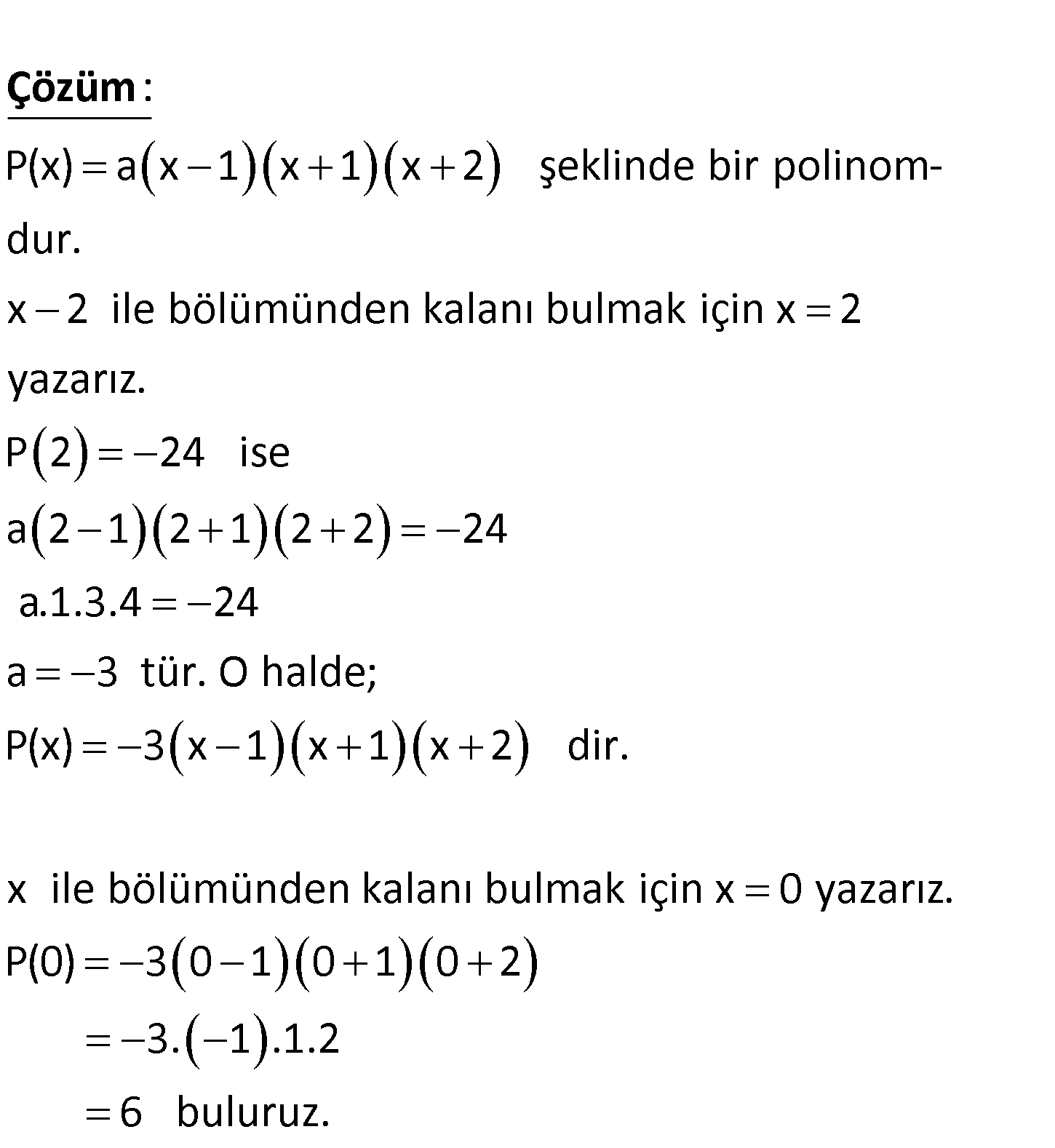
12.SORU


13.SORU
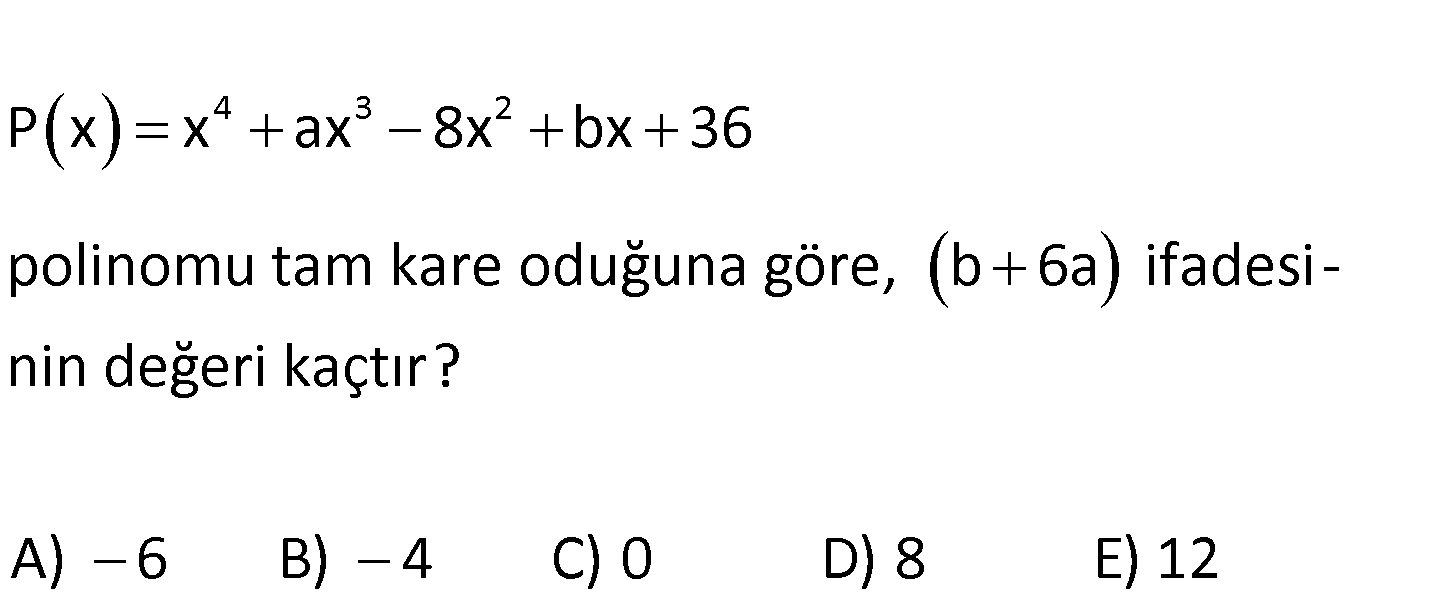

14.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 2 x 2 .P x x m 9 olduğuna göre, P x 1 ‘in x 3 ile bölümünden kalan kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 2 2 x 2 P x x m 9 x 2 için sol taraf 0 olur. 2 2 .P 2 2 m 9 0.P 2 4 m 9 0 13 m m 13 tür. m değerini : Çözüm 2 2 2 yukarıda yerine yazarsak; x 2 P x x 13 9 x 2 P x x 4 x 4 x 2 x 2 P x x 2 dir. x 2 x 2 P x 1 ‘in x 3 ile bölümünden kalanı bulmak için x 3 0 x 3 P( 3 1) P 2 hesaplanmalı. P x x 2 P 2 2 2 4 bulunur. 27
www.matematikkolay.net 3 2 x 1 .P x x 7x m 1 olduğuna göre, P x polinomunun katsayılar top – lamı kaçtır? A) 11 B) 13 C) 14 D) 15 E) 17 3 2 3 2 (x 1) P(x) x 7x m 1 x 1 yazarsak (1 1) P(1) 1 7.1 m 1 0 1 7 m 1 0 9 m m 9 dur. O hald : e; (x Çözüm 3 2 3 2 3 2 2 2 2 2 2 1) P(x) x 7x 9 1 (x 1) P(x) x 7x 8 (x 1) P(x) x x 8x 8 (x 1) P(x) x x 1 8(x 1) (x 1) P(x) x x 1 8(x 1)(x 1) (x 1) P(x) x x 1 8(x 1)(x 1) (x 1) P(x) x 1 2 2 x 8(x 1) P(x) x 8x 8 dir. Polinomun katsayılar toplamı 1 8 8 17 dir. 28
www.matematikkolay.net İkinci dereceden P x polinomu x 4 , x 1 , x 2 ile bölündüğünde kalanlar sırasıyla 4, 4, 22 oluyor. Buna göre, Px in x 3 ile bölümünden kalan kaç – tır? A) 2 B) 4 C) 6 D) 8 E) 9 www.matematikkolay.net 2 P(4) 4, P(1) 4 ve P( 2) 22 dir. P(x) ax bx c şeklinde bir polinom olsun. Sırasıyla b : Çözüm u değerleri yazalım. x 4 için 16a 4b c 4 x 1 için a b c 4 x 2 için 4a 2b c 22 Bu denklemlerden, a b c değerlerini bulalım. 2.denklemi 2 ile çarpalım ve denklemleri taraf tarafa toplayalım. 1 1 16a 4b c 4 2a 2b 2c 8 4a 2b c 22 18a 18 a 1 dir. a b c 4 b c 3 4a 2b c 22 2b c 18 / b c 3 2b c 18 b c 3 2b c 18 3b 15 b 5 tir. b c 2 2 3 5 c 3 c 8 dir. O halde; P(x) x 5x 8 polinomudur. P(3) sorulmuştu. P(3) 3 5.3 8 9 15 8 17 15 2 buluruz. 29
www.matematikkolay.net P x üçüncü dereceden bir polinomdur. P x polinomu x 2 , x 1 ve x 2 ile tam bölünebilmektedir. P x polino munun x 1 ile bölümünden kalan 36 olduğuna göre, P x polinomunun x ile bölümünden kalan kaçtır? A) 24 B) 18 C) 0 D) 18 E) 24 P(x) a(x 2)(x 1)(x 2) şeklinde yazabiliriz. P(1) 36 ise; a’yı bulalım. P(1) a(1 2)(1 ) : 1 (1 2) Çözüm 36 a.( 1).2.3 36 6a a 6 dır. O halde; P(x) 6(x 2)(x 1)(x 2) polinomunu bulmuş buluruz. Bize P(0) sorulmuş. P(0) 6(0 2)(0 1)(0 2) P(0) 6( 2)(1)(2) P(0) 6.( 4) P(0) 24 buluruz. 30
Baş katsayısı 2 olan ikinci dereceden bir P x poli – nomunda P 2 P 1 4 olduğuna göre, P 3 P 0 far kı kaçtır? A) 8 B) 9 C) 10 D) 12 E) 15 2 2 2 P x 2x ax b P(2) P(1) 4 2.2 2a b 2.1 a b 4 8 a b : 2 Çözüm 2 a b 2 2 4 6 a 4 a 2 dir. P(x) 2x 2x b dir. O halde; P(3) P(0) 2.3 2.3 b 0 0 b 18 6 b b 12 buluruz. www.matematikkolay.net 35
2.dereceden bir P x polinomu için P x P x 1 2x 4 eşitliği veriliyor. P 0 2 olduğuna göre, P x aşağıdakile 2 2 2 2 2 rden hangisidir? A) x 3x 2 B) x 3x 2 C) x 4x 2 D) x 4x 2 E) x 5x 2 2 2 P x , ikinci dereceden bir polinom ise; P x ax bx c olmalı. P 0 2 c 2 dir. P x P x 1 2x 4 ax x : bx 2 a Çözüm 2 2 1 b x 1 2 2x 4 ax bx 2 2 ax 2ax a bx b 2 2 2x 4 2ax a b 2x 4 2a 2 a 1 dir. 1 b 4 b 3 tür. P x x 3x 2 bulunur. 40
www.matematikkolay.net 2 2 2 2 P 3x 1 x x 1 olduğuna göre, P 6x 1 aşağıdakilerden hangisi – dir? A) x x 2 B) 2x x 1 C) 4x 2 2 2 x 1 D) 4x 3x 1 E) 4x x 1 2 2 x 1 3 2 P(3x 1) x x 1 x 1 x yerine yazalım 3x 1 in tersi 3 P(3 x 1) x x 1 x 1 x 1 P(x) 3 3 : Çözüm 2 2 2 2 1 6x 1 1 6x 1 1 P(6x 1) 1 3 3 6x 6x 1 3 3 2x 2x 1 4x 2x 1 buluruz. 41
2 2 P x bir polinomdur. x a .P x x x a 3 eşitliği daima doğru olduğuna göre, P 1 kaçtır? A) 5 B) 4 C) 0 D) 2 E) 4 www.matematikkolay.net 2 2 2 2 0 2 x a .P x x x a 3 x a olsun. a a .P : a a a a 3 12:00 AM Çözüm 2 a a 2 2 2 3 0 a 3 a 3 tür. Buna göre; x 3 .P x x x 3 3 x 3 .P x x x 12 x 3 .Px x 4 x 3 P(x) x 4 tür. P 1 1 4 5 buluruz. 57
3 x ax 1 x 1 .P x olduğuna göre, P 1 kaçtır? A) 13 B) 8 C) 6 D) 5 E) 3 www.matematikkolay.net 3 0 3 x 1 yazarak, a’yı bulalım. x ax 1 x 1 .P(x) 1 a 1 1 1 .P(1) a : 0 olmalıdır. x 1 x 1 .P(x) Çözüm olur. x 1 2 x x 1 x 1 2 .P(x) P(x) x x 1 dir. O halde; P(1) 1 1 1 3 buluruz. 58
2 Başkatsayısı 2 olan üçüncü dereceden P x polino – mu x x 2 ile tam bölünüyor. P x in katsayıları topl 2 amı 2 olduğuna göre, P x aşağıdakilerden hangisi ile tam bölünür? A) 2x 3 B) x 2 C) x 1 D) x E) 2x 3 2 P(x), başkatsayısı 2 olan üçüncü dereceden bir polinom ise; P(x) 2 x x 2 x a şeklinde bir l : po Çözüm 2 inomdur. Katsayıları toplamı 2 ise P(1) 2 dir. Yerine yazalım. P(1) 2 1 1 2 1 a 2 2 2 2 1 a 1 1:00 AM 2 3 a dır. 2 3 P(x) 2 x x 2 x 2 P(x) 2 2 2x 3 x x 2 2 2 P(x) x x 2 2x 3 2x 3’e tam bölünür. 63
www.matematikkolay.net 3. dereceden bir P x polinomu x 1, x 1, x 2 ile tam bölünebilmektedir. P x polinomunun x 2 ile bölümün den kalan 24 ise x ile bölümünden kalan kaçtır? A) 2 B) 4 C) 6 D) 7 E) 8 P(x) a x 1 x 1 x 2 şeklinde bir polinomdur. x 2 ile bölümünden kalanı bulmak için x 2 yazarı : z Çözüm . P 2 24 ise a 2 1 2 1 2 2 24 a.1.3.4 24 a 3 tür. O halde; P(x) 3 x 1 x 1 x 2 dir. x ile bölümünden kalanı bulmak için x 0 yazarız. P(0) 3 0 1 0 1 0 2 3. 1 .1.2 6 buluruz. 82
P x polinomunu x 2 ve x 3 e tam bölünebi – len baş katsayısı 5 olan bir polinomdur. P 1 x polinomunun x 2 ile bölümünden kalan 12 olduğuna göre, P 1 kaçtır? A) 32 B) 30 C) 28 D) 24 E) 16 www.matematikkolay.net P(x) polinomu 3.dereceden bir polinom ve iki çarpanı verilmişse P(x)’i şöyle ifade edebi : liriz Çözüm 2 3 2 . P(x) (ax b).(x 2)(x 3) P(x) (ax b)(x x 6) x lü terimin katsayısı 5 olması için a 5 olmalıdır. P(x) (5x b)(x x 6) x 2 0 yapan x değeri 2 dir. P(1 x)’ te x yerine 2 yazarsak P(3) olur. 2 2 Yani; P(3) 12 dir. Bunu kullanarak b’yi bulalım. P(x) (5x b)(x x 6) idi. P(3) (5.3 b)(9 3 6) 12 (15 b)(6) 12 15 b 2 b 13 dir. P(x) (5x 13)(x x 6) polinomunu elde ederiz. P(1) ( 8 )(4) 32 buluruz. 91
4 3 2 P x x ax 8x bx 36 polinomu tam kare oduğuna göre, b 6a ifadesi – nin değeri kaçtır? A) 6 B) 4 C) 0 D) 8 E) 12 2 2 4 3 2 3 2 2 2 4 3 2 2 2 P x x cx 6 şeklinde olmalıdır. x cx 6x cx c x 6cx 6x 6cx 36 x 2cx 12x c x 12cx 36 P : Çözüm 4 x x 3 2 ax 8x bx 36 4 x 3 2 2 2 2cx 12x c x 12cx 36 3 3 2cx ax a 2c dir. 12cx bx b 12c b 6a 12c 6.2c 12c 12c 0 bulunur. 33
www.matematikkolay.net P x polinomu x 3 ile bölündüğünde bölüm Q x , kalan 1 dir. Q x polinomu x 1 ile bölündüğün – de kalan 2 2 dir. Buna göre, P x polinomunun x 2x 3 ile bölümünden kalan aşağıdakilerden hangisidir? A) 2x 2 B) 2x 4 C) 2x 7 D) 2x 9 E) x 1 P x x 3 .Q x 1 yazılabilir. Q x x 1 R x 2 bu polinomu yukarıya yazalım. P x x 3 . x 1 R x 2 1 olur : . P x x Çözüm 2 2 Burası tam bölünür 3 x 1 R x 2 x 3 1 x 2x 3 R x 2x 6 1 x 2x 3 R x 2x 7 Kalan 2x 7 buluruz. www.matematikkolay.net 34

