Soru Sor sayfası kullanılarak Polinomlar konusu altında Karmaşık sayılı kökü olan polinomlar ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU

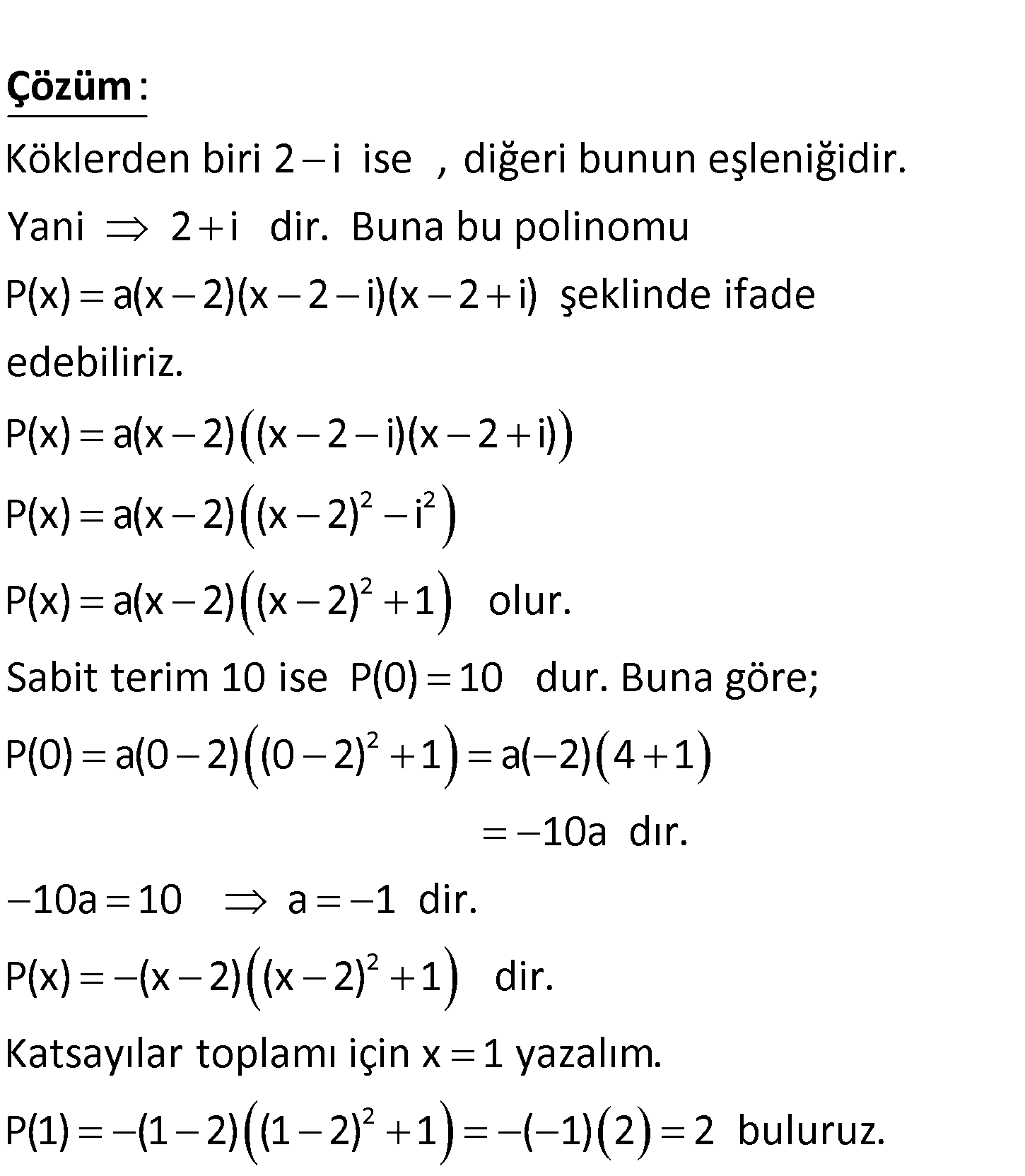
5.SORU


6.SORU


7.SORU


8.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Başkatsayısı 2 olan, 2i ve 3i karmaşık sayılarını kök kabul eden dördüncü dereceden gerçel katsayı – lı P x polinomunun sabit terimi kaçtır? A) 48 B) 52 C) 56 D) 60 E) 72 Karmaşık sayıların eşlenikleri de polinomun kökleridir. Buna göre; P(x) polinomunu P(x) 2 : (x 2 Çözüm 2 2 i)(x 2i)(x 3i)(x 3i) şeklinde yazabiliriz. Sabit terim P(0) 2(0 2i)(0 2i)(0 3i)(3i) P(0) 2( 4i )( 9i ) 02.04.2009 7 2 buluruz. www.matematikkolay.net 13
Baş katsayısı 1 olan, i ve 2i karmaşık sayılarını kök kabul eden dördüncü dereceden gerçel katsayı lı P x polinomu için P 0 kaçtır? A) 2 B) 4 C) 6 D) 7 E) 8 www.matematikkolay.net Dördüncü dereceden gerçek katsayılı bir polinomun iki kökü i ve 2i ise diğer iki kökü bu kö : k Çözüm 4 lerin eşleniği olan i ve 2i olmalıdır. Başkatsayısı 1 olan P(x) polinomu; P(x) (x i)(x i)(x 2i)(x 2i) olur. P(0) (0 i)(0 i)(0 2i)(0 2i) P(0) ( i).i.( 2i).2i 4.i 4.1 4 bulunur. 16
www.matematikkolay.net P x baş katsayısı 2 ve sabit terimi 13 olan üçüncü dereceden gerçek katsayılı bir polinomdur. P x 0 d enkleminin köklerinden biri 3 2i olduğuna göre P 2 kaçtır? : Bir kökü 3 2i ise,diğeri 3 2i dir. Buna göre; P(x) 2.(x 3 2i)(x 3 2i)(x a) şeklinde yaz bil a Çözüm iriz. P(0) 2.( 3 2i)( 3 2i)( a) 13 2.(9 4).( a) 13 Şub.13 .(a) 13 1 a dir. 2 1 P(x) 2.(x 3 2i)(x 3 2i)(x ) 2 1 P(2) 2.(2 3 2i)(2 3 2i)(2 ) 2 5 2.( 1 2i)( 1 2i) 2 5 2.(1 4) 2 2 5 .(1 4) 2 5.5 25 buluruz. 18
Üçüncü dereceden gerçek katsayılı bir polinom kökleri 2 ve 2- i dir. Bu polinomunun sabit terimi 10 olduğuna göre, bu polinomun katsayılar toplamı kaçtır? A) -2 B) 0 C) 2 D) 4 E) 6 Köklerden biri 2 i ise , diğeri bunun eşleniğidir. Yani 2 i dir. Buna bu polinomu P(x) : Çözüm 2 2 2 2 a(x 2)(x 2 i)(x 2 i) şeklinde ifade edebiliriz. P(x) a(x 2) (x 2 i)(x 2 i) P(x) a(x 2) (x 2) i P(x) a(x 2) (x 2) 1 olur. Sabit terim 10 ise P(0) 10 dur. Buna göre; P(0) a(0 2) (0 2) 1 a( 2) 4 1 2 2 10a dır. 10a 10 a 1 dir. P(x) (x 2) (x 2) 1 dir. Katsayılar toplamı için x 1 yazalım. P(1) (1 2) (1 2) 1 ( 1) 2 2 buluruz. www.matematikkolay.net 25
www.matematikkolay.net Köklerden ikisi 4 2i ve 6 olan üçüncü dereceden rasyonel katsayılı P x polinomunun sabit terimi 120 d ir. Buna göre, P 1 değeri kaçtır? A) 40 B) 50 C) 65 D) 75 E) 80 Köklerden biri 4 2i ise , diğeri bunun eşleniğidir. Yani 4 2i dir. Buna bu polinomu P(x : Çözüm 2 2 2 2 ) a(x 6)(x 4 2i)(x 4 2i) şeklinde ifade edebiliriz. P(x) a(x 6) (x 4 2i)(x 4 2i) P(x) a(x 6) (x 4) 2i P(x) a(x 6) (x 4) 4 olur. Sabit terim 120 ise P(0) 120 dir. Buna göre; P(0) a(0 6) (0 4) 4 a( 6) 1 2 2 6 4 120a dır. 120a 120 a 1 dir. P(x) (x 6) (x 4) 4 tür. P(1) (1 6) (1 4) 4 ( 5) 9 4 65 buluru z. www.matematikkolay.net 37
www.matematikkolay.net Baş katsayısı 1 olan, i ve 3i karmaşık sayılarını kök kabul eden üçüncü dereceden P x polinomu veri – liyor. P 0 6 olduğuna göre, üçüncü kök kaçtır? A) 2 B) 1 C) 1 D) 2 E) 3 P(x) 1. x i x 3i x a şeklinde bir polinomdur. P 0 6 bilgisini kullanarak a’yı bulalım. 1. 0 i 0 : Çözüm 3.kök burada 3i 0 a 6 i.3i. 0 a 6 3.a 6 a 2 dir. P(x) 1. x i x 3i x 2 şeklinde bir polinomdur. 3.Kök : x 2 0 x 2 dir. 71
www.matematikkolay.net P x polinomunun katsayıları toplamı P 1 dir. Başkatsayısı 2 olan dördüncü dereceden rasyonel katsayılı P x polinomunun köklerinden iki tanesi 3 2 ve 2i olduğuna göre, P x polinomunun katsayılar toplamı kaçtır? A) 12 B) 20 C) 36 D) 40 E) 60 Polinomun katsayıları rasyonel ise, diğer kökler, verilen köklerin eşlenikleri olmalıdır : . 3 2 Çözüm 2 2 nin eşleniği 3 2 dir. 2i nin eşleniği 2i dir. Buna göre; P x 2 x 3 2 x 3 2 x 2i x 2i Katsayılar toplamı P(1) ile bulabiliriz. P 1 2 1 3 2 1 3 2 1 2i 1 2i 2 2 2 2 2 1 2i 1 2i 2 2 2 1 4 24 25 02.02.2005 20 buluruz. 72
www.matematikkolay.net P x başkatsayısı 2 ve sabit terimi 13 olan üçüncü dereceden gerçek katsayılı bir polinomdur. P x 0 den kleminin köklerinden biri 3 2i olduğu – na göre, P 2 kaçtır? A) 35 B) 30 C) 25 D) 20 E) 15 2 P(x) (x 3 2i)(2x bx c) Bir kökü 3 2i ise diğer kökü 3 2i dir. Toplamları 6, çarpı : mları 13 tür Çözüm 2 2 2 . Buna uygun 2.dereceden denklem x 6x 13 Buna göre; P(x) (ax b)(x 6x 13) tür. Baş katsayı 2 ise a 2 dir. Sabit terim 13 ise; P(0) b.13 13 b 1 dir. P(x) (2x 1)(x 6x 13) polinomunu elde ederiz. P(2) 5.5 25 buluruz. 150

