Soru Sor sayfası kullanılarak Üçgende Açıortay konusu altında Paraleller arası açıortay, Açıortaylardan çevre bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

3.SORU

4.SORU
5.SORU

6.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
ABC üçgen DE // BC B K ve CK açıortay AB 10 birim AC 8 birim Yukarıdaki verilere göre, ADE üçgeninin çevresi kaç birimdir? A) 15 B) 16 C) 18 D) 20 E) 24 Çözüm: DE//BC olduğundan m KBC m(DKB) dir. Yöndeş Açılar BDK üçgeni ikizkenar bir üçgen olur. BD a ise DK a dır. mKCB m(EKC) dir. Yöndeş Açılar ECK üçgeni ikizkenar bir üçgen olur. EC b ise KE b dir. AB 10 ise AD 10 a dır. AC 8 ise AE 8 b dir. ADE üçgeninin çevresi; 10:00 AM a b10 b 20 birim buluruz. 3
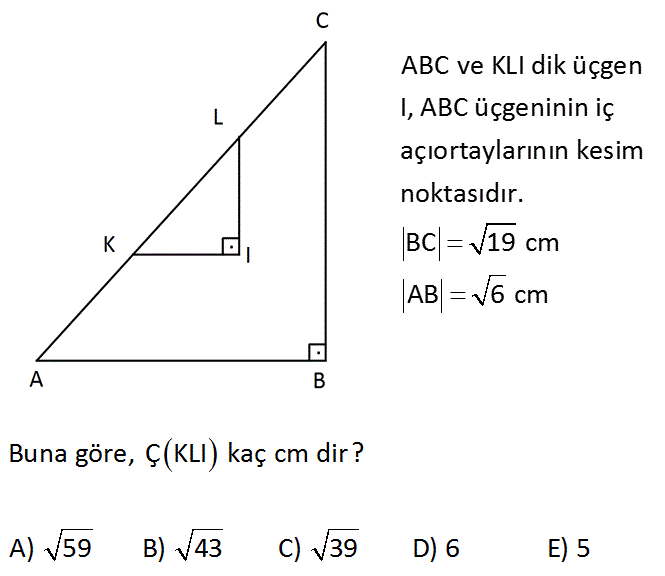
ABC ve KLI dik üçgen I, ABC üçgeninin iç açıortaylarının kesim noktasıdır. BC 19 cm AB 6 cm Buna göre, ÇKLI kaç cm dir? A) 59 B) 43 C) 39 D) 6 E) 5 Çözüm: İki üçgen de dik üçgen olduğundan; KI//AB ve LI//BC dir. AI açıortayının ayırdığı açılara a diyelim. m KIA a olur. İç ters açılar AKI üçgeni ikizkenar bir üçgen olur. KI KA x olur. 2 2 Aynı durum diğer açıortay için de geçerli. LI y olur. Çevre KLI x y z AC dir. AC 19 6 Pisagor AC 25 AC 5 buluruz. 8
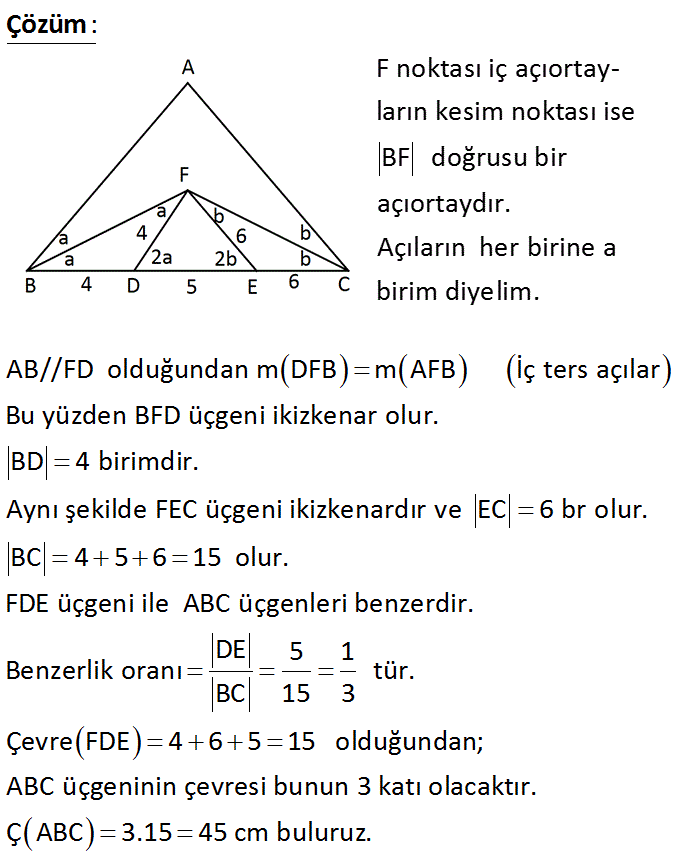
ABC üçgen F: iç açıortayların kesim noktası DF // AB EF // AC DF 4 cm EF 6 cm DE 5 cm Yukarıda verilenlere göre, ÇABC kaç cm dir? A) 45 B) 36 C) 30 D) 24 E) 21 Çözüm: F noktası iç açıortayların kesim noktası ise BF doğrusu bir açıortaydır. Açıların her birine a birim diyelim. AB//FD olduğundan mDFB mAFB İç ters açılar Bu yüzden BFD üçgeni ikizkenar olur. BD 4 birimdir. Aynı şekilde FEC üçgeni ikizkenardır ve EC 6 br olur. BC 4 5 6 15 olur. FDE üçgeni ile ABC üçgenleri be nzerdir. DE 5 1 Benzerlik oranı tür. BC 15 3 Çevre FDE 4 6 5 15 olduğundan; ABC üçgeninin çevresi bunun 3 katı olacaktır. Ç ABC 3.15 45 cm buluruz. 11
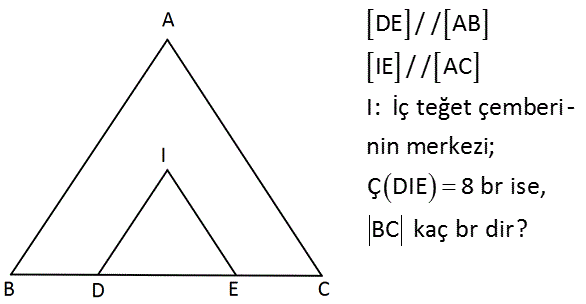
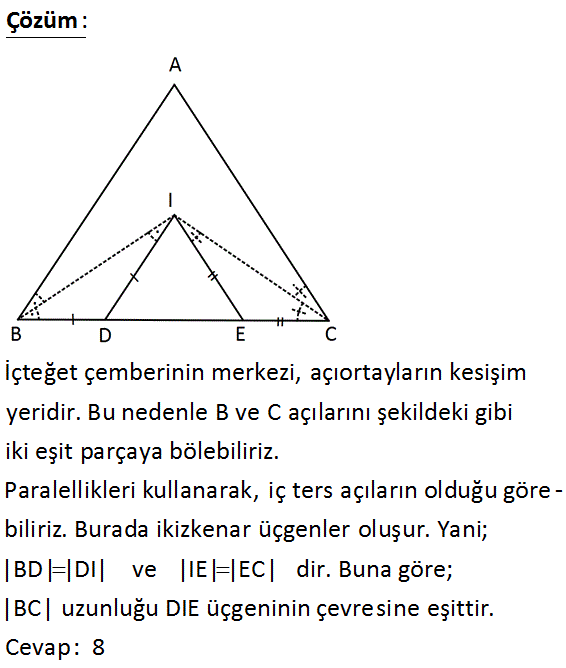
DE / / AB IE / / AC I: İç teğet çemberi – nin merkezi; Ç DIE 8 br ise, BC kaç br dir? : Çözüm İçteğet çemberinin merkezi, açıortayların kesişim yeridir. Bu nedenle B ve C açılarını şekildeki gibi iki eşit parçaya bölebiliriz. Paralellikleri kullanarak, iç ters açıların olduğu göre – biliriz. Burada ikizkenar üçgenler oluşur. Yani; |BD| |DI| ve |IE| |EC| dir. Buna göre; |BC| uzunluğu DIE üçgeninin çevresine eşittir. Cevap: 8 13
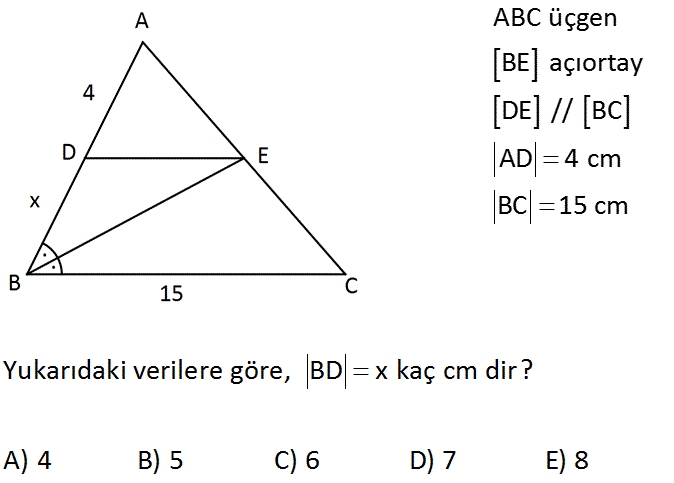
ABC üçgen BE açıortay DE // BC AD 4 cm BC 15 cm Yukarıdaki verilere göre, BD x kaç cm dir? A) 4 B) 5 C) 6 D) 7 E) 8 : Çözüm 2 2 x 6 [DE] // [BC] olduğundan; m(EBC) m(BED) dir. (İç ters açılar) BDE ikizkenar üçgendir ve |DE| x olur. ADE üçgeni ile ABC üçgeni arasındaki benzerlikten; x 4 15 4 x 4x x 60 x 4x 60 0 (x 10)(x 6) 0 x 6 buluruz. 32
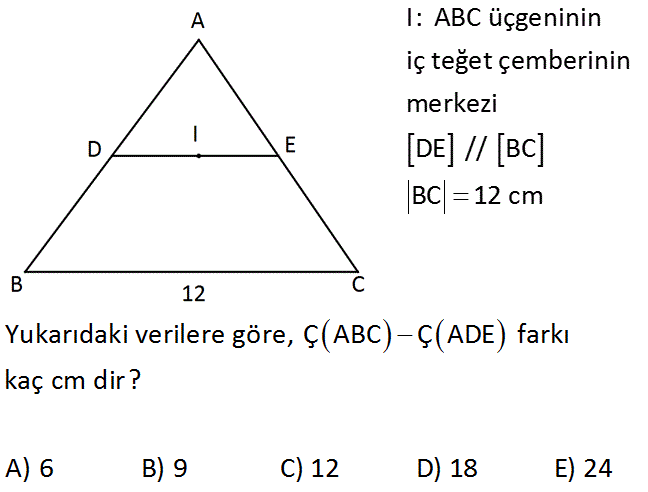
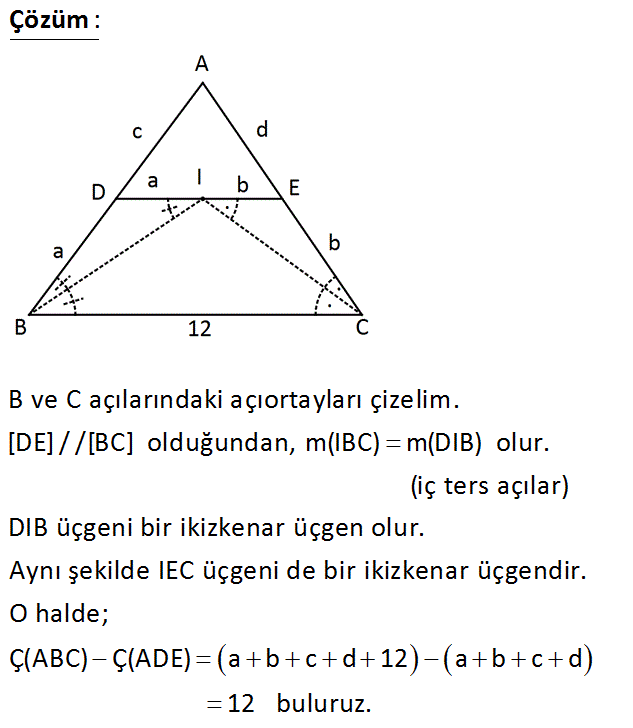
I: ABC üçgeninin iç teğet çemberinin merkezi DE // BC BC 12 cm Yukarıdaki verilere göre, ÇABC ÇADE farkı kaç cm dir? A) 6 B) 9 C) 12 D) 18 E) 24 : Çözüm B ve C açılarındaki açıortayları çizelim. [DE] / /[BC] olduğundan, m(IBC) m(DIB) olur. (iç ters açılar) DIB üçgeni bir ikizkenar üçgen olur. Aynı şekilde IEC üçgeni de bir ikizkenar üçgendir. O halde; Ç(ABC) Ç(ADE) a b c d 12 a b c d 12 buluruz.

