Soru Sor sayfası kullanılarak Üçgende Açıortay konusu altında Açıortayda kollara inen yükseklik, Açıortaydan kenarlara inilen dikme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU

3.SORU

4.SORU
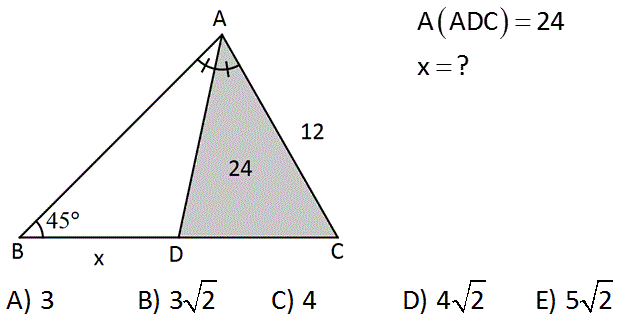
5.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
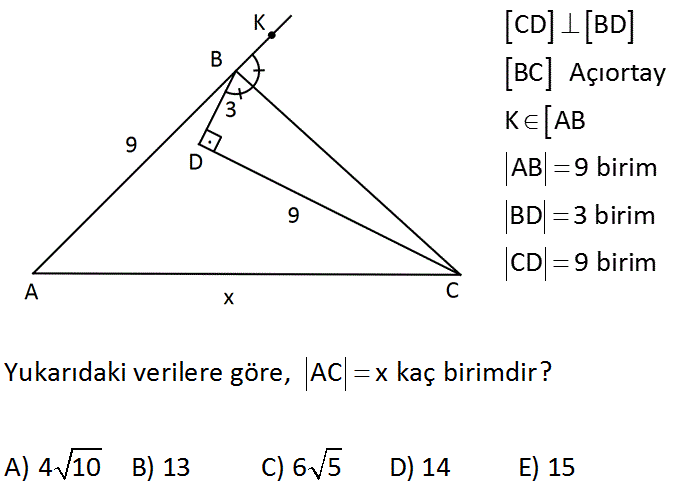
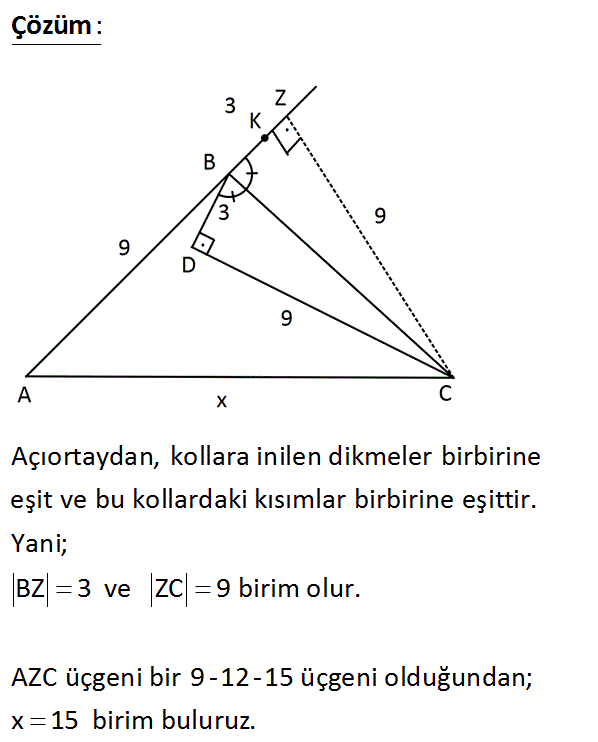
CD BD BC Açıortay K AB AB 9 birim BD 3 birim CD 9 birim Yukarıdaki verilere göre, AC x kaç birimdir? A) 4 10 B) 13 C) 6 5 D) 14 E) 15 Çözüm: Açıortaydan, kollara inilen dikmeler birbirine eşit ve bu kollardaki kısımlar birbirine eşittir. Yani; BZ 3 ve ZC 9 birim olur. AZC üçgeni bir 9 -12-15 üçgeni olduğundan; x 15 birim buluruz. 5
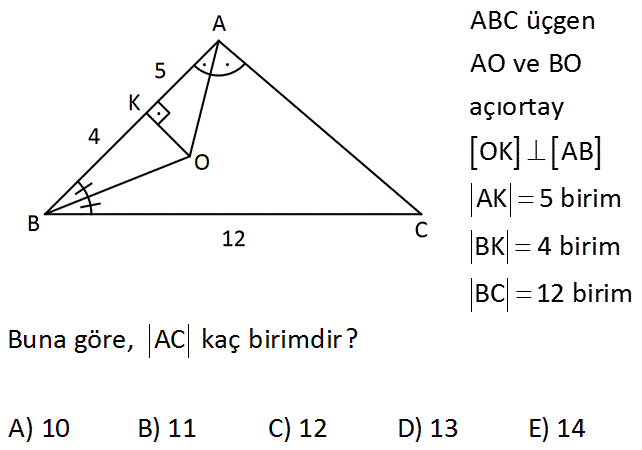
ABC üçgen AO ve BO açıortay OK AB AK 5 birim BK 4 birim BC 12 birim Buna göre, AC kaç birimdir? A) 10 B) 11 C) 12 D) 13 E) 14 Çözüm: Açıortayda kollara inilen dikmeler birbirine eşittir. BK 4 ise BM 4 tür. MC 12 4 8 olur. LC 8 olur. AK 5 ise AL 5 olur. AC 5 8 13 br buluruz. 10
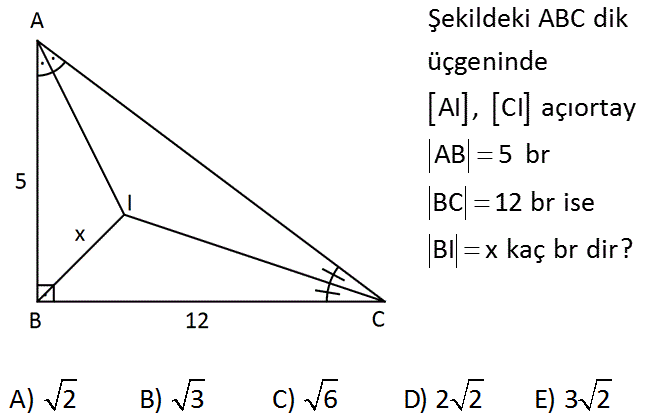
Şekildeki ABC dik üçgeninde AI , CI açıortay AB 5 br BC 12 br ise BI x kaç br dir? A) 2 B) 3 C) 6 D) 2 2 E) 3 2 : Çözüm Açıortaydan kenarlara inilen dikmeler birbirine eşittir. Üçgendeki hipotenüs 13′ tür. (5-12-13 üçgeni) 13 5 a 12 a 13 17 2a 2a 4 a 2 dir. x a 2 2 2 buluruz. (45- 45-90 üçgeni) 12
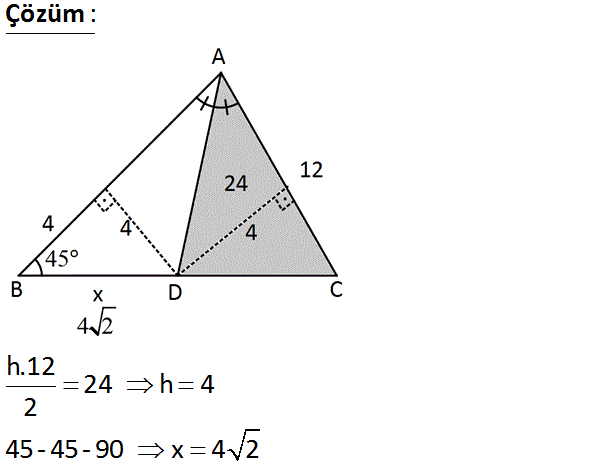
AADC 24 x ? A) 3 B) 3 2 C) 4 D) 4 2 E) 5 2 : Çözüm h.12 24 h 4 2 45- 45-90 x 4 2 19
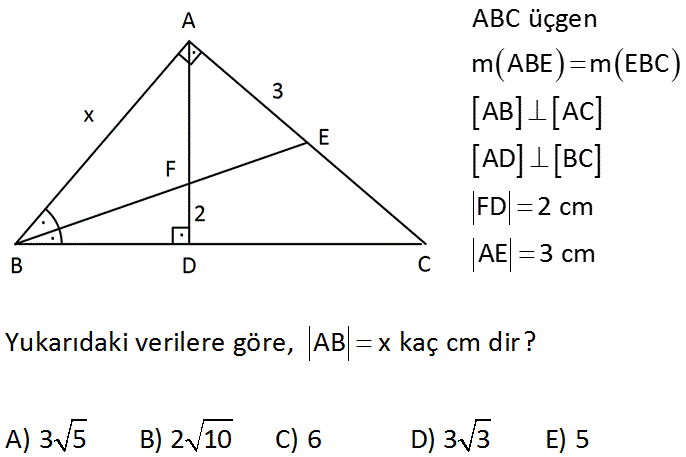
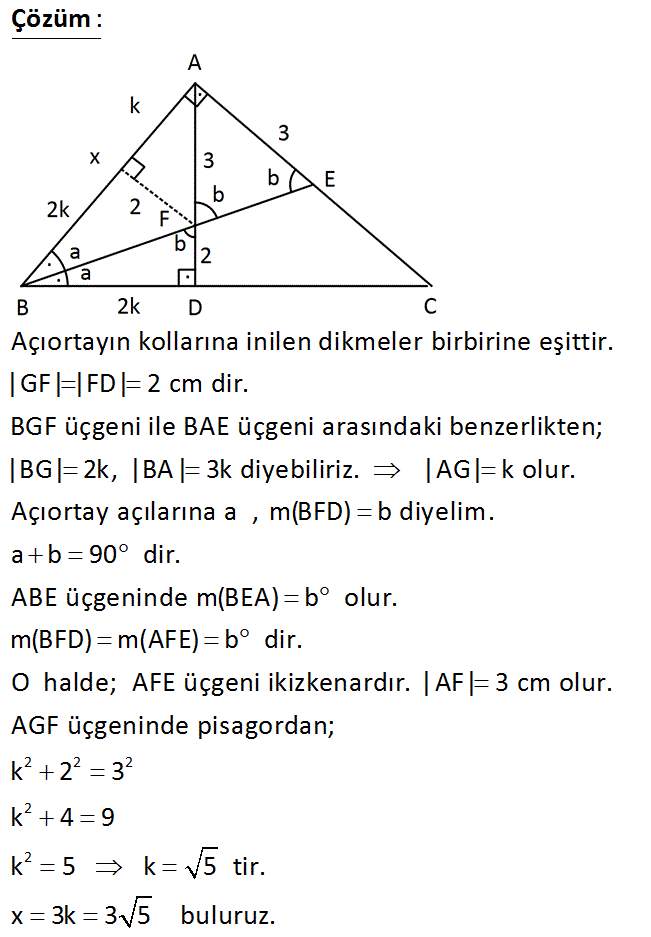
ABC üçgen m ABE m EBC AB AC AD BC FD 2 cm AE 3 cm Yukarıdaki verilere göre, AB x kaç cm dir? A) 3 5 B) 2 10 C) 6 D) 3 3 E) 5 Çözüm: Açıortayın kollarına inilen dikmeler birbirine eşittir. |GF| |FD| 2 cm dir. BGF üçgeni ile BAE üçgeni arasındaki benzerlikten; |BG| 2k, |BA| 3k diyebiliriz. |AG| k olur. Açıortay açılarına a , m(BFD) 2 2 2 2 2 b diyelim. a b 90 dir. ABE üçgeninde m(BEA) b olur. m(BFD) m(AFE) b dir. O halde; AFE üçgeni ikizkenardır. |AF| 3 cm olur. AGF üçgeninde pisagordan; k 2 3 k 4 9 k 5 k 5 tir. x 3k 3 5 bulur uz. 30


Çıktı almak istiyorum pdf atar mısınız