Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında L’hospital ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

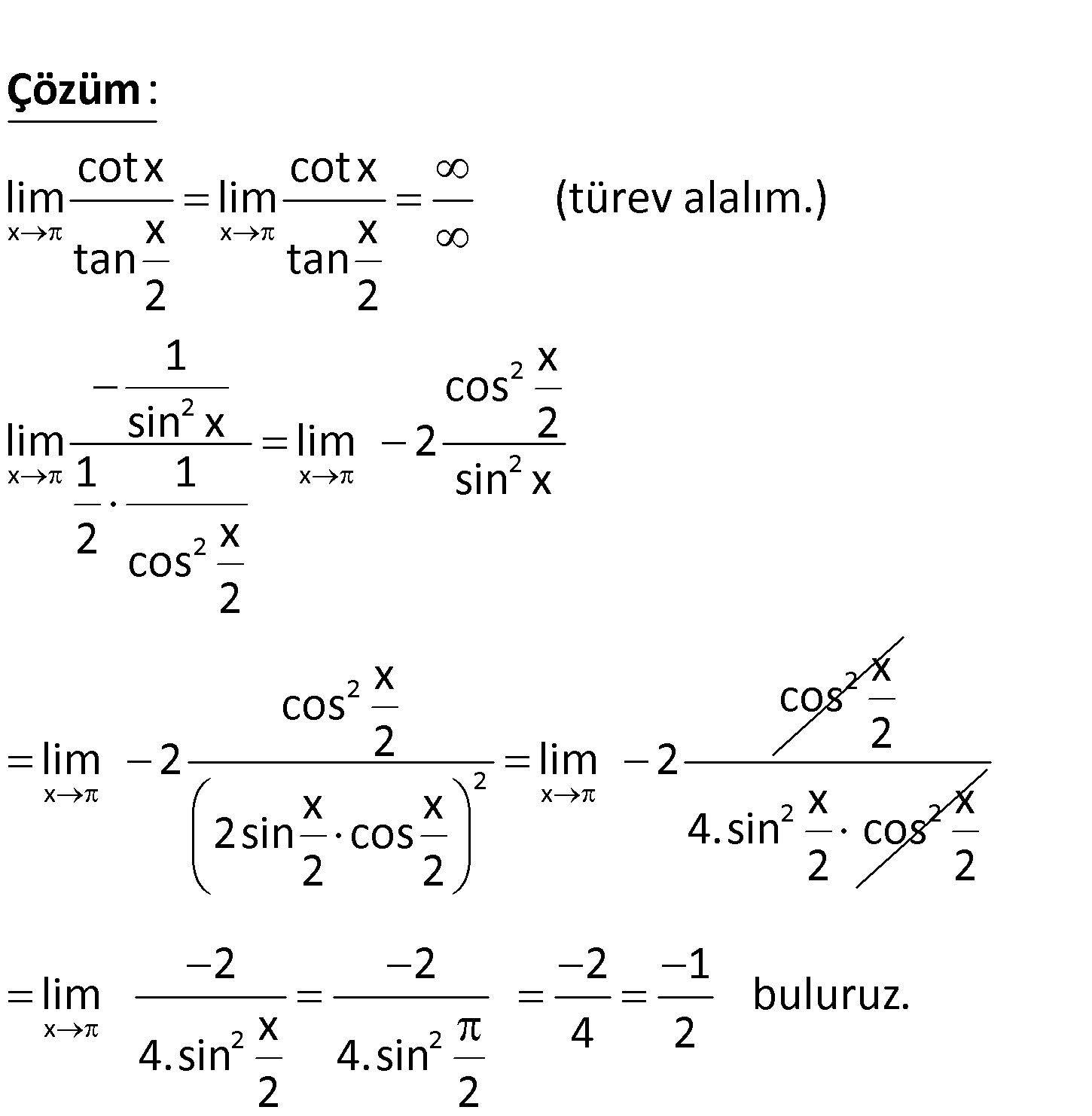
2.SORU


3.SORU

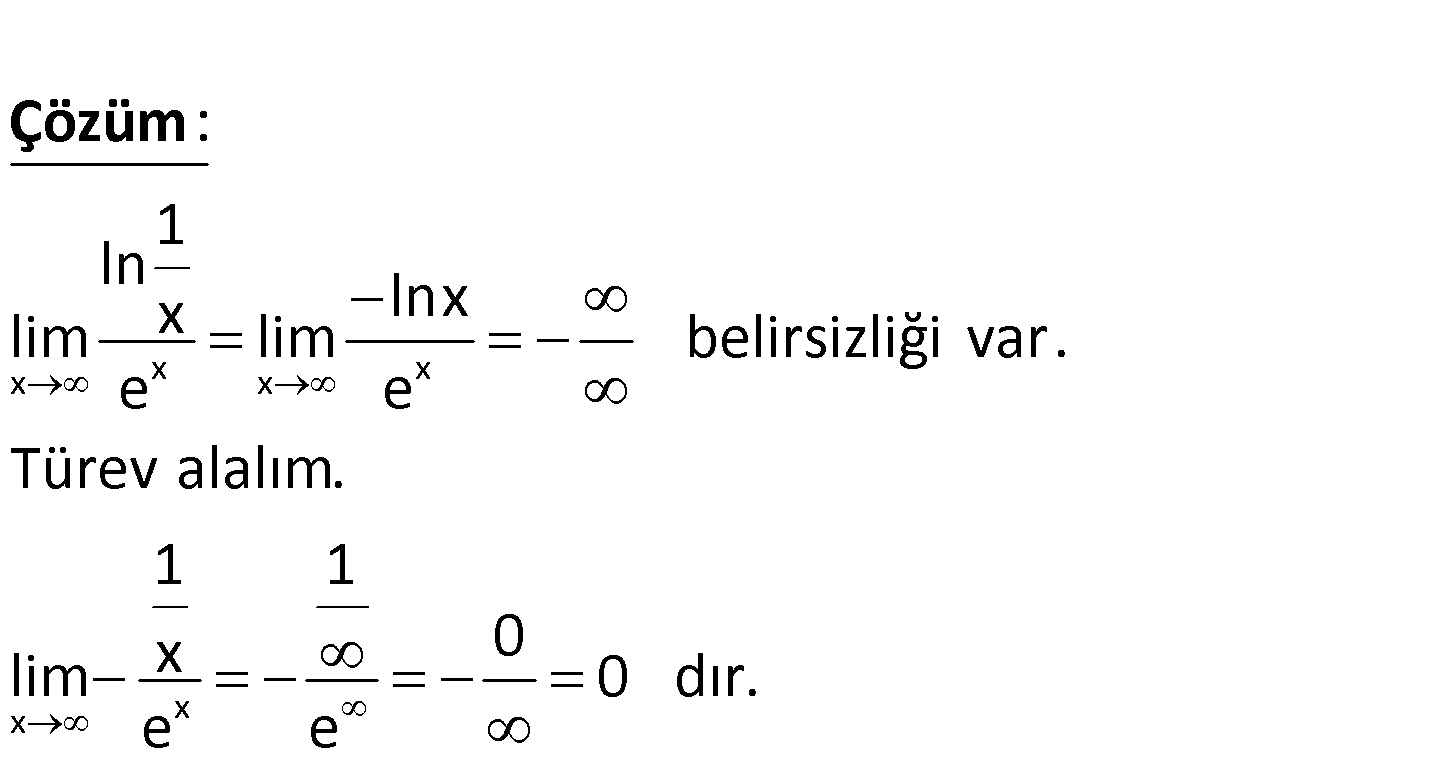
4.SORU
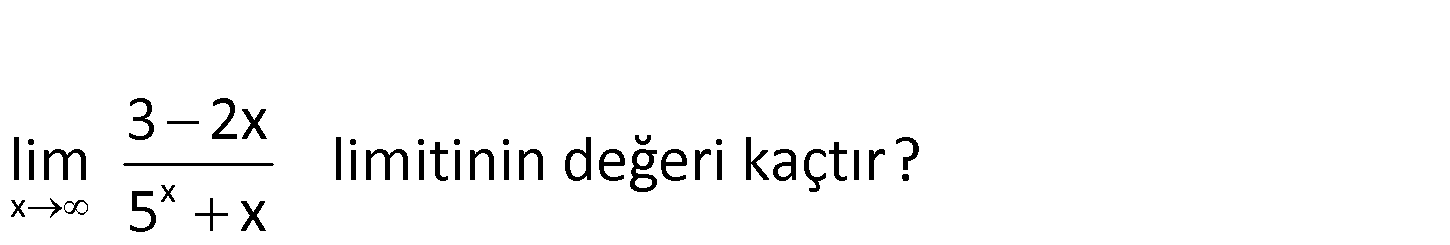

5.SORU
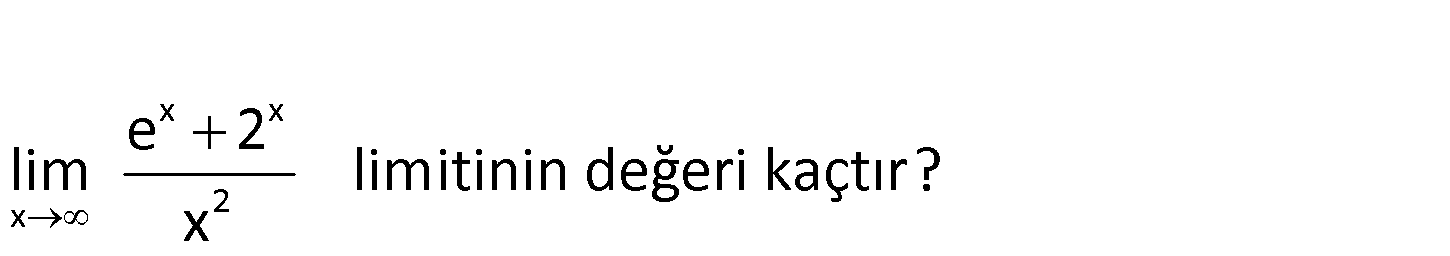

6.SORU

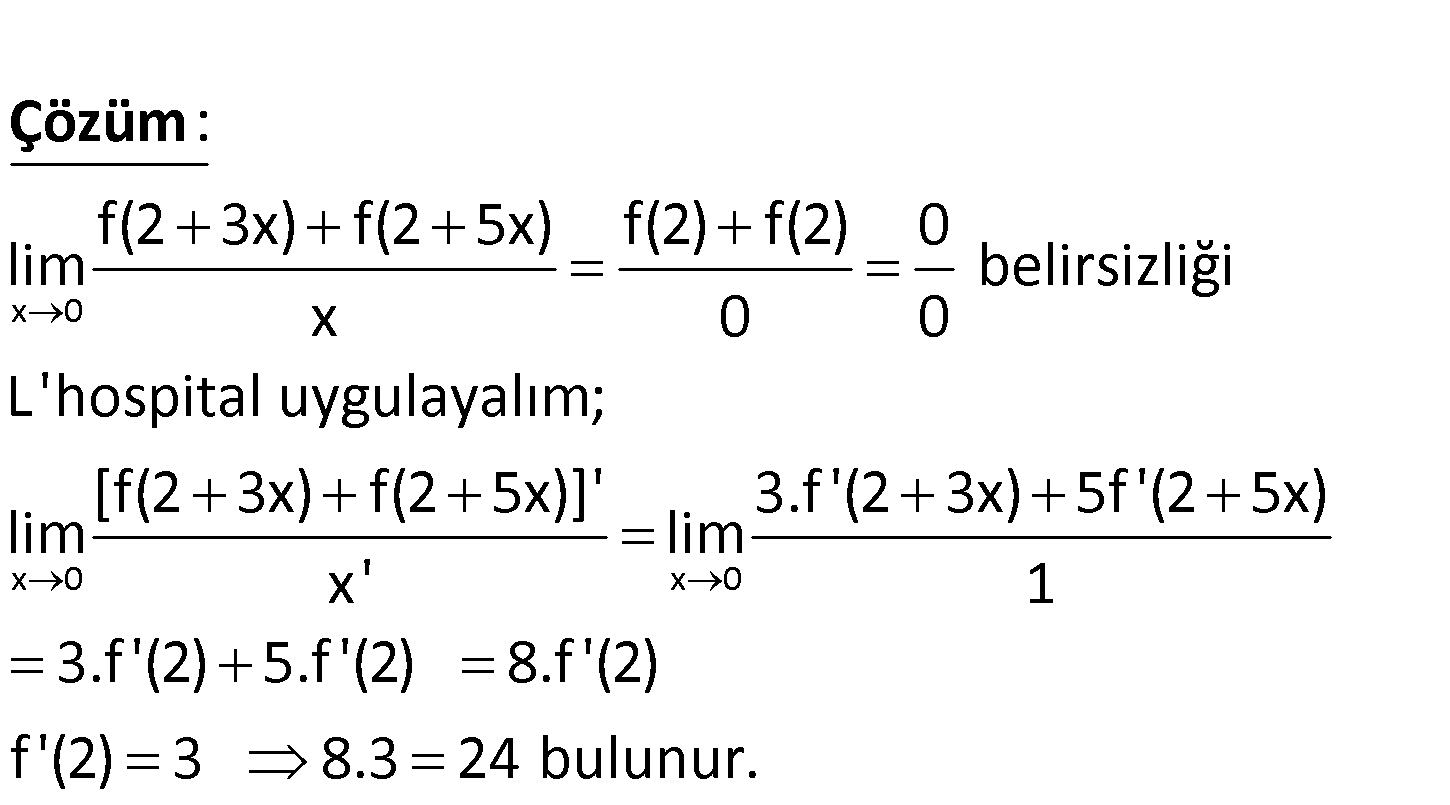
7.SORU

8.SORU
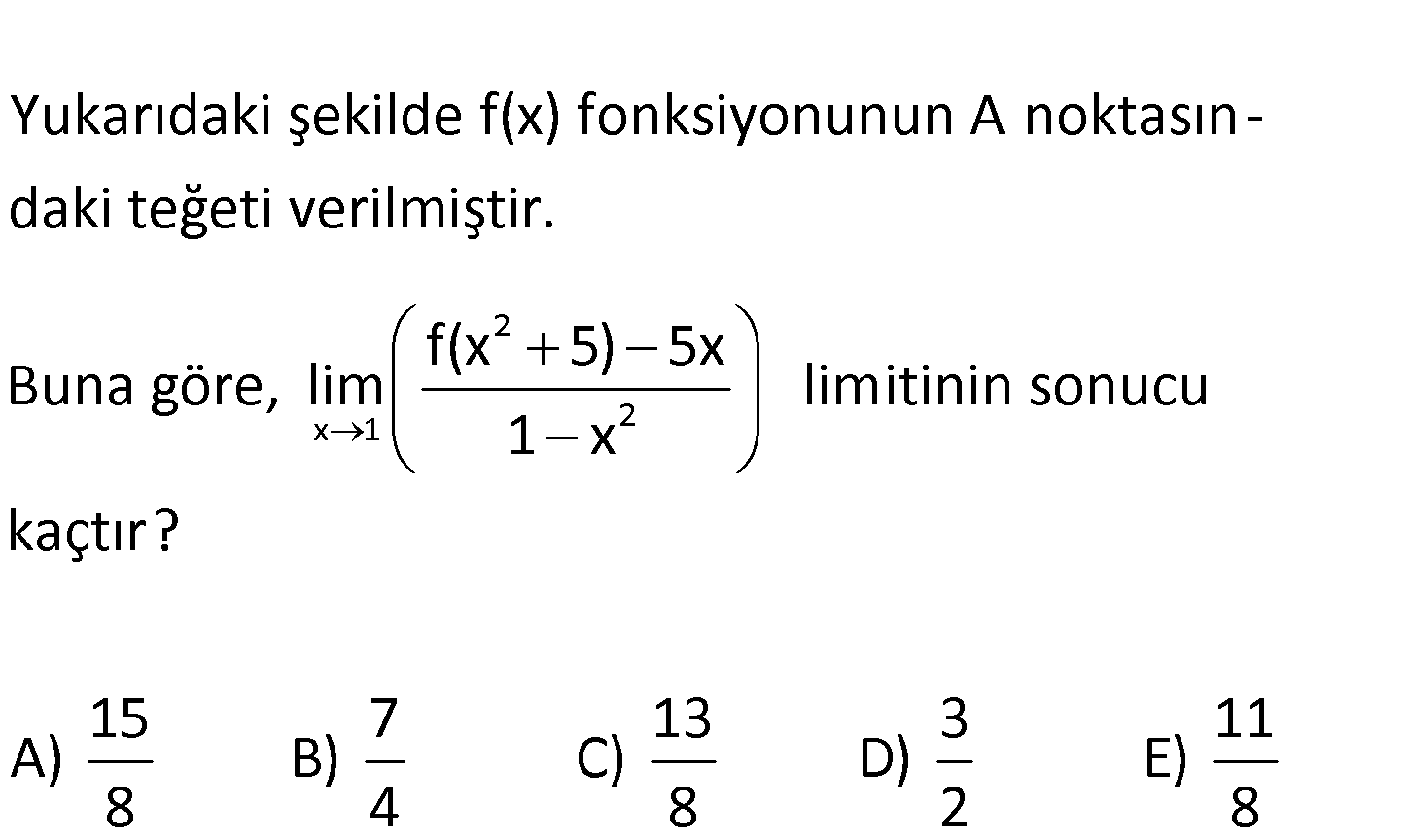

9.SORU

10.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
x cotx lim limitinin değeri kaçtır? x tan 2 www.matematikkolay.net x x 2 x x 2 cotx cotx lim lim (türev alalım.) x x tan tan 2 2 1 cos lim sin x lim 2 1 1 2 x cos 2 : Çözüm 2 2 2 2 x 2 x x 2 sin x x x cos cos 2 2 lim 2 lim 2 x x 2sin cos 2 2 2 x 2 x 4.sin cos 2 2 x 2 2 2 2 2 1 lim buluruz. x 4 2 4.sin 4.sin 2 2 24
2x x e 2x lim limitinin değeri kaçtır? ln x 1 www.matematikkolay.net 2x x 2x 2 x x e 2x lim belirsizliği var dır. Türev alalım. ln(x 1) 2e 2 lim lim (x 1)(2e 1 1 : x Çözüm x 2) buluruz. 26
x x 1 ln lim x limitinin değeri kaçtır? e www.matematikkolay.net x x x x x x 1 ln x lnx lim lim belirsizliği var. e e Türev alalım. 1 1 x 0 lim 0 dır e e : Çözüm . 32
x x 3 2x lim limitinin değeri kaçtır? 5 x x x x x 3 2x lim belirsizliği var. Türev alalım. 5 x 2 2 2 lim 0 dır. 5 ln5 1 5 l : n5 1 Çözüm 33
x x x 2 e 2 lim limitinin değeri kaçtır? x www.matematikkolay.net x x x 2 2 e 2 e 2 lim belirsizliği x L’hospital uygulayalım. Payın ve paydanın türevi : ni alal Çözüm x x x x x 2 x ım. e 2 .ln2 lim belirsizliği 2x Tekrar türev alalım. e 2 .ln 2 lim bulunur. 2 34
www.matematikkolay.net x 0 f ‘ gerçek sayılarda sürekli bir fonksiyon, f(2) 0 ve f ‘(2) 3 olduğuna göre, f(2 3x) f(2 5x) lim x limitinin değeri kaçtır? A) 28 B) 24 C) 20 D) 16 E) 12 x 0 x 0 f(2 3x) f(2 5x) f(2) f(2) 0 lim belirsizliği x 0 0 L’hospital uygulayalım; [f(2 3x) f( : 2 5 lim Çözüm x 0 x)]’ 3.f ‘(2 3x) 5f ‘(2 5x) lim x’ 1 3.f ‘(2) 5.f ‘(2) 8.f ‘(2) f ‘(2) 3 8.3 24 bulunur. 41
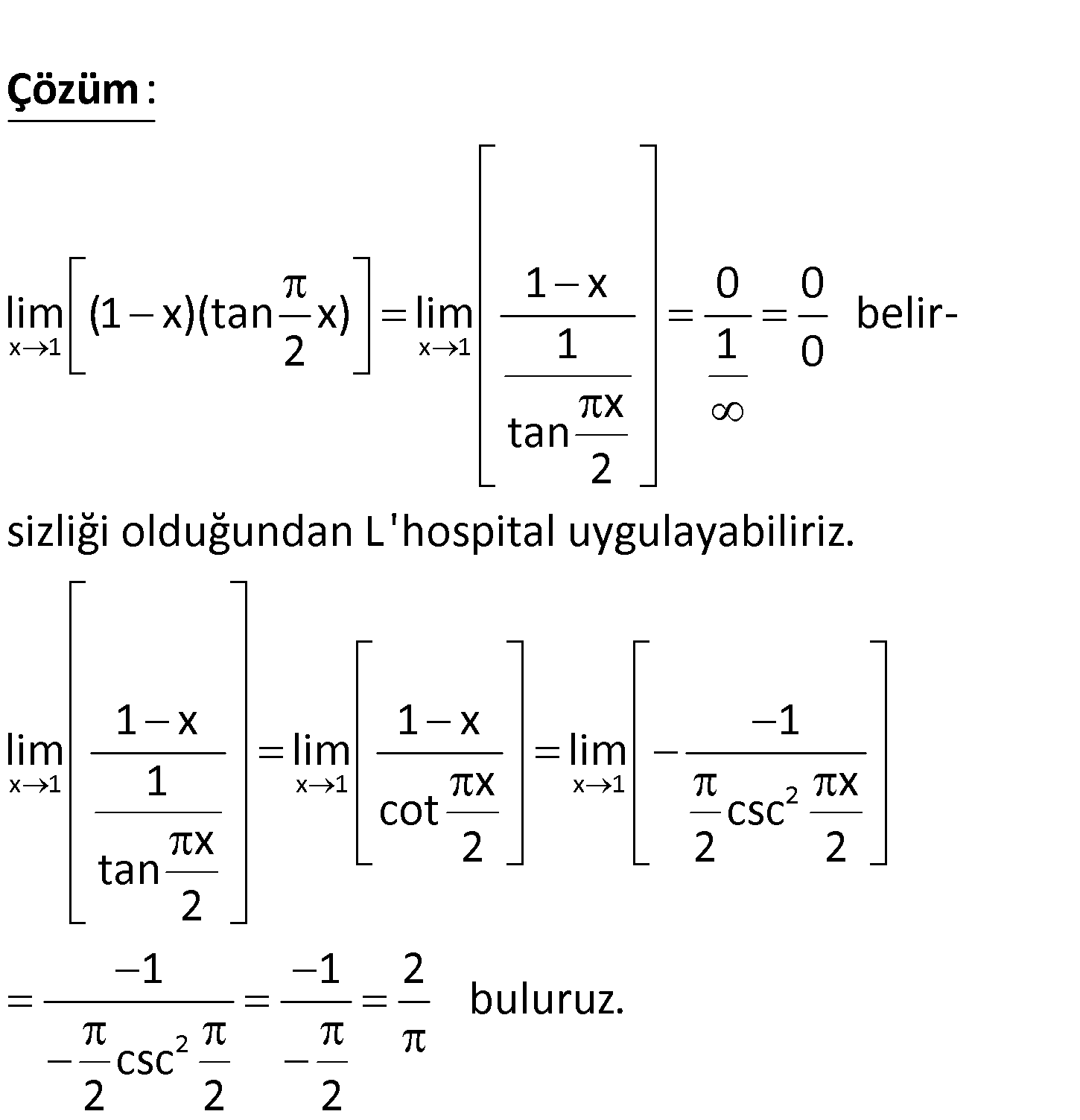
x 1 lim (1 x)(tan x) ? 2 x 1 x 1 1 x 0 0 lim (1 x)(tan x) lim belir- 2 1 1 0 x tan 2 sizliği olduğundan : Çözüm x 1 x 1 x 1 2 2 L’hospital uygulayabiliriz. 1 x 1 x 1 lim lim lim 1 x x cot csc x 2 2 2 tan 2 1 1 2 buluruz. csc 2 2 2 85
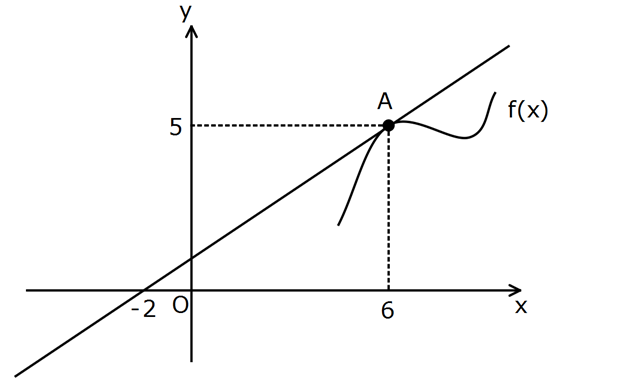
2 x 1 Yukarıdaki şekilde f(x) fonksiyonunun A noktasın – daki teğeti verilmiştir. f(x 5) Buna göre, lim 2 5x limitinin sonucu 1 x kaçtır? 15 7 13 3 11 A) B) C) D) E) 8 4 8 2 8 2 x 1 2 x f(x 5) 5x f(6) 5 5 5 0 lim 2 belirsizliği 1 x 1 1 0 0 L’hospital uygulayabiliriz. l : im Çözüm 2 1 2xf ‘(x 5) 5 2f ‘(1 5) 5 2f ‘(6) 5 2x 2 2 5 (x 6 noktasındaki teğetin eğimi f ‘(6) dir.) 8 5 5 15 2 5 5 8 4 4 15 buluruz. 2 2 2 8 www.matematikkolay.net 88
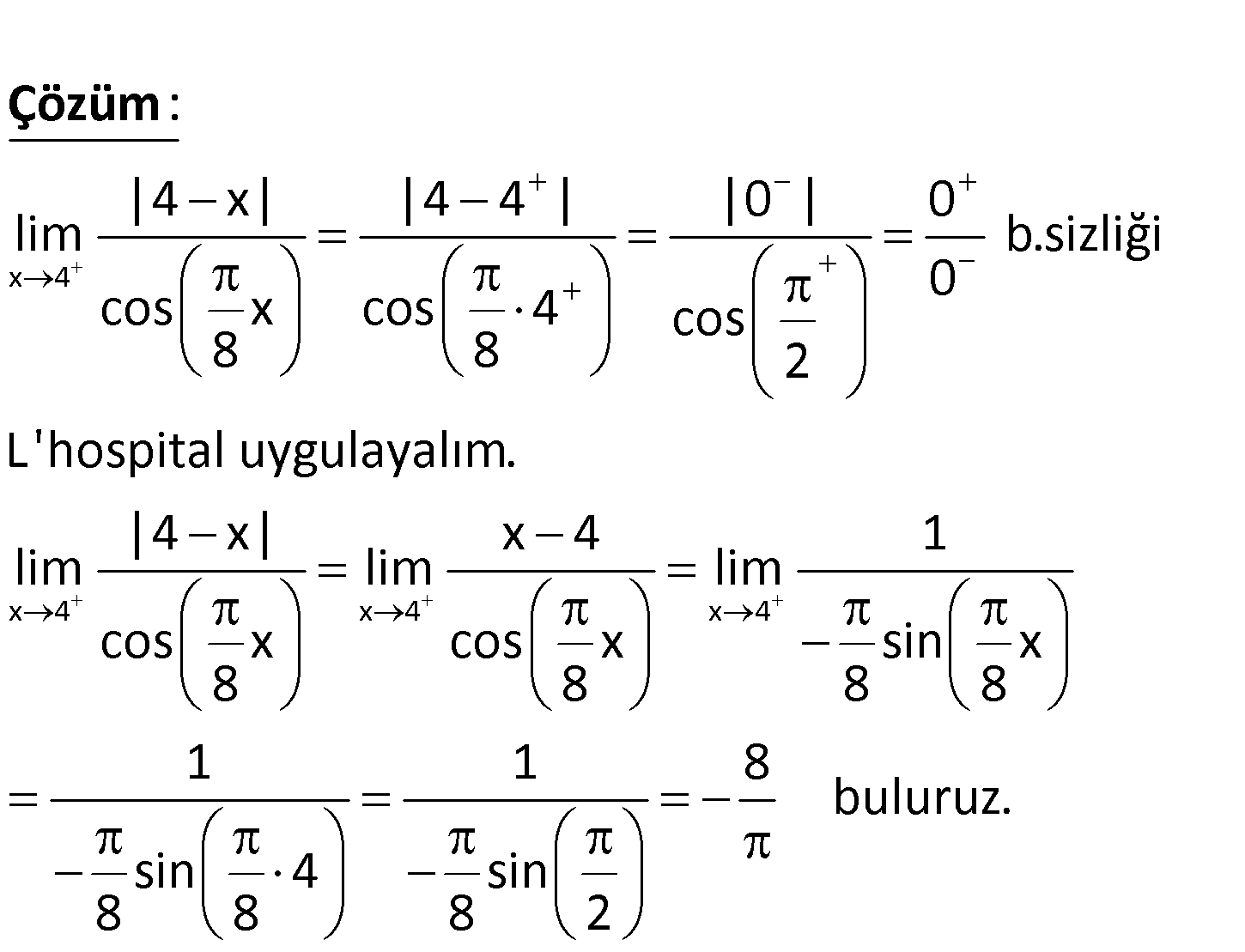
x 4 |4 x| lim ifadesinin değeri nedir? cos x 8 x 4 |4 x| |4 4 | |0 | 0 lim b.sizliği 0 cos x cos 4 cos 8 8 2 L’hospital uy : gu Çözüm x 4 x 4 x 4 layalım. |4 x| x 4 1 lim lim lim cos x cos x sin x 8 8 8 8 1 1 8 buluruz. sin 4 sin 8 8 8 2 www.matematikkolay.net 105
www.matematikkolay.net 3 2 2 a 3 olmak üzere, (a 3)x ax 5x 1 y 5 x eğrisinin yatay asimptotunun denklemi aşağıdaki – l erden hangisidir? A) y 3 B) y 2 C) y 1 D) y -2 E) y -3 3 x Bu eğrinin yatay asimptotu var sa, x sonsuza giderken bir limiti var demektir. (a 3)x ax lim : Çözüm 2 2 2 x x 5x 1 k 5 x belirsizliği var. L ‘hospital uygulayalım. 3.(a 3)x 2ax 5 lim 2x belirsizliği var. Bir daha L ‘hospital uygulayalım. 6.(a 3)x 2a lim 2 belirsizliği artık yok. Pay da x ‘ ten kurtu x lmalı ki bu ifade sonsuza gitmesin. O zaman a 3 olmalıdır. Bu durumda 6.(3 3)x 2.3 lim 3 buluruz. 2 Asimptotun denklemi y 3 tür. www.matematikkolay.net 114

