Soru Sor sayfası kullanılarak Trigonometri-2 konusu altında Şekilli tanjant toplam fark soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…

1.SORU
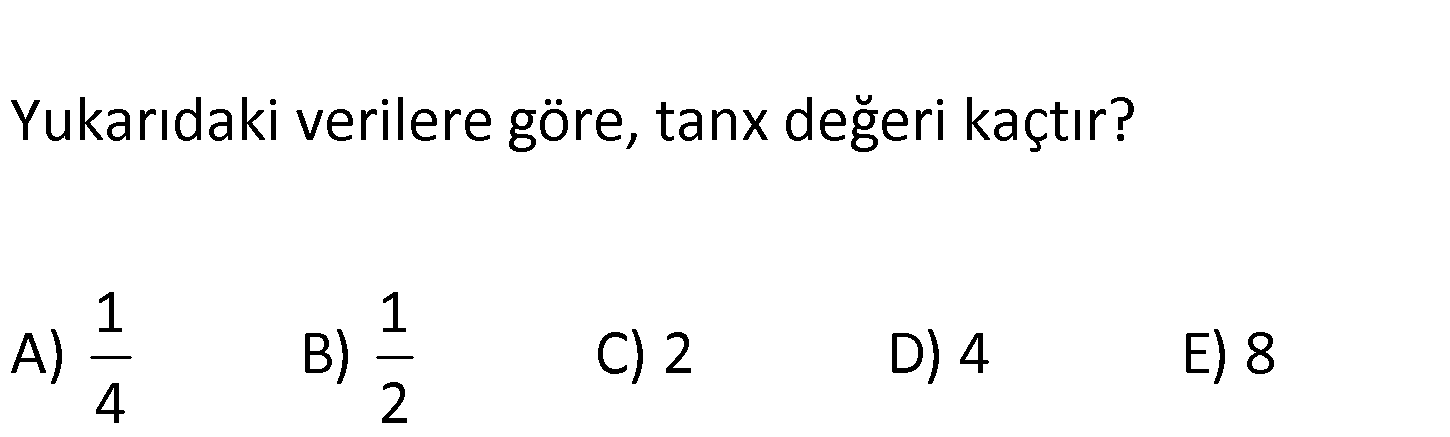
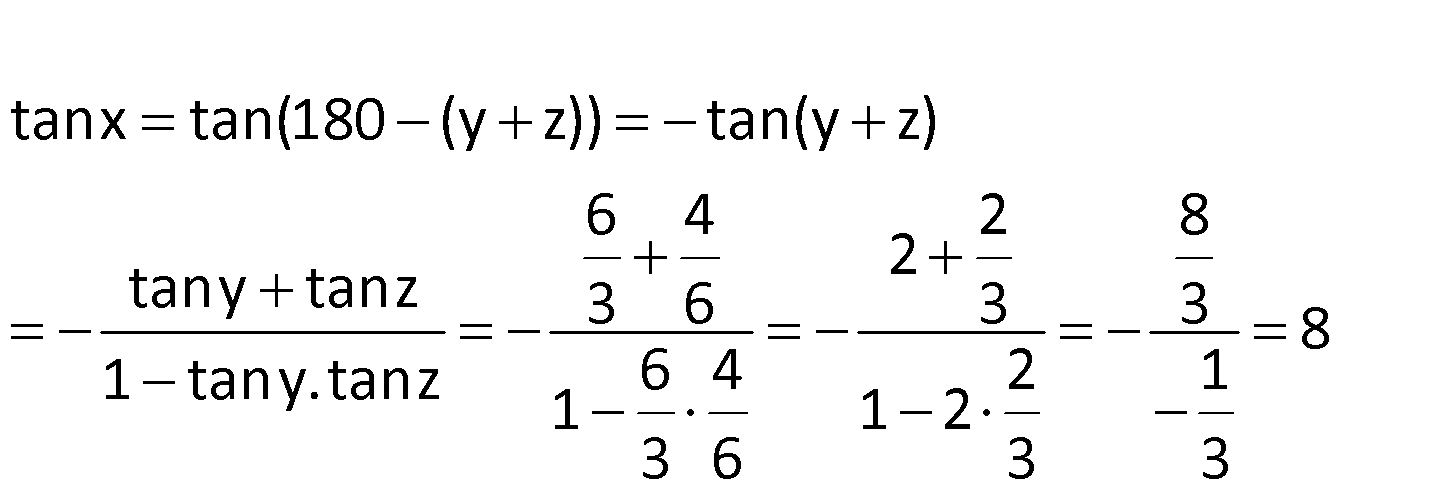
2.SORU
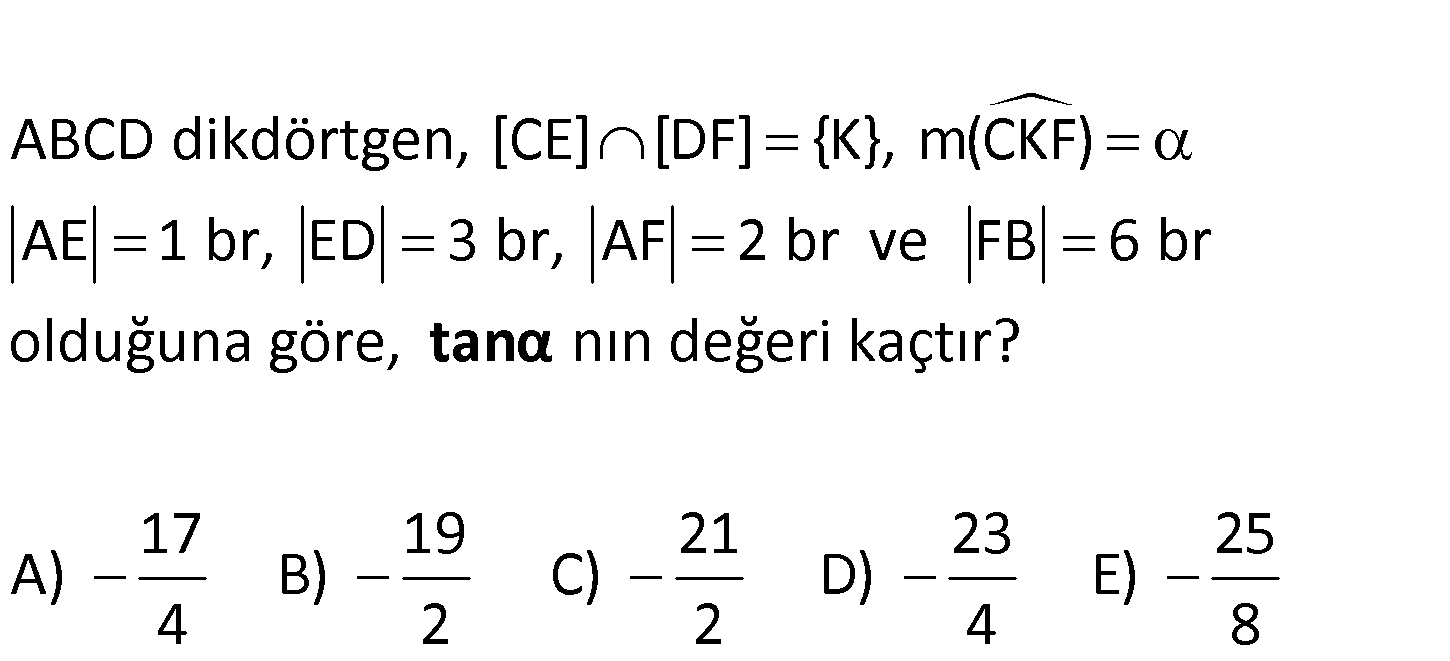
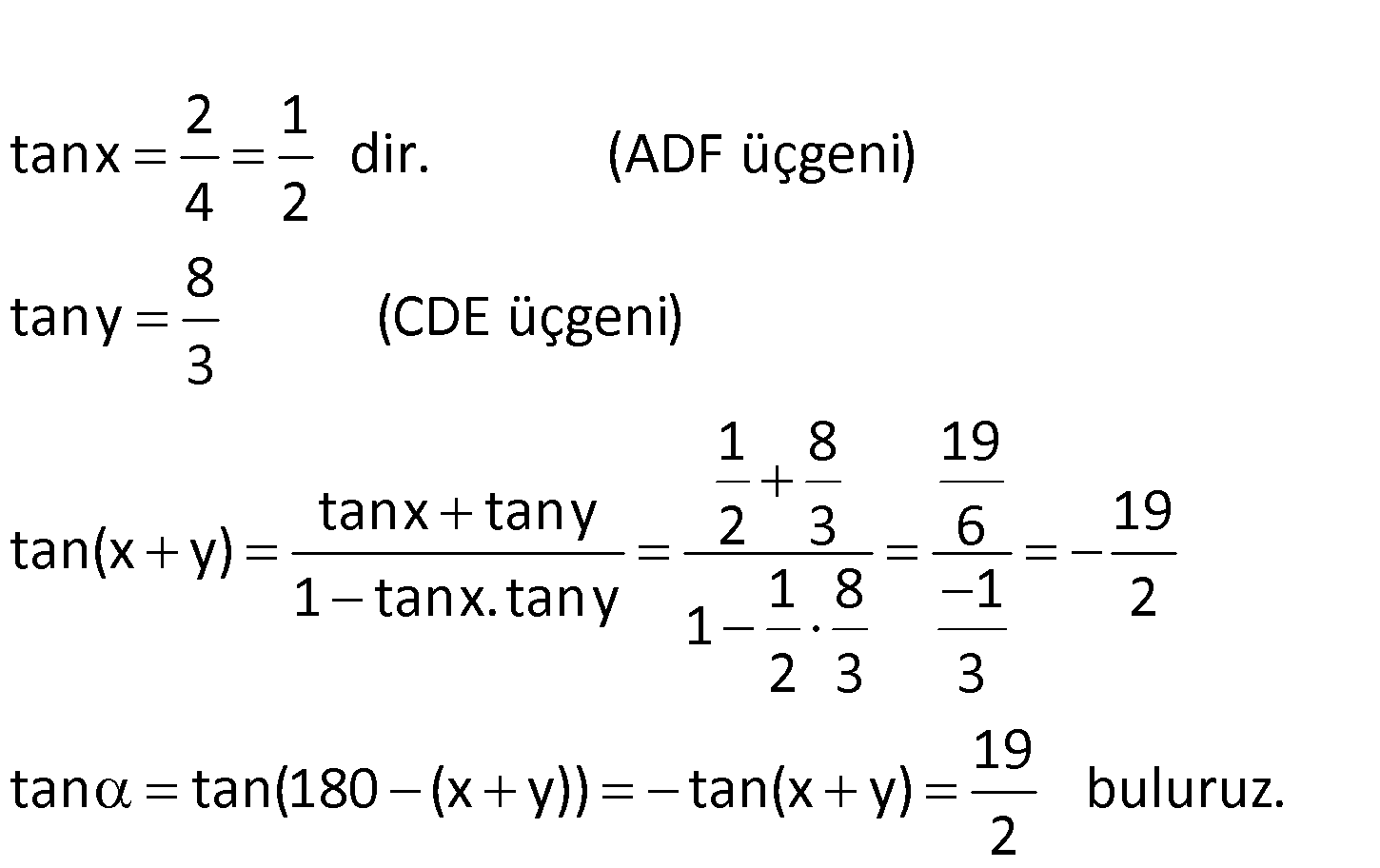
3.SORU
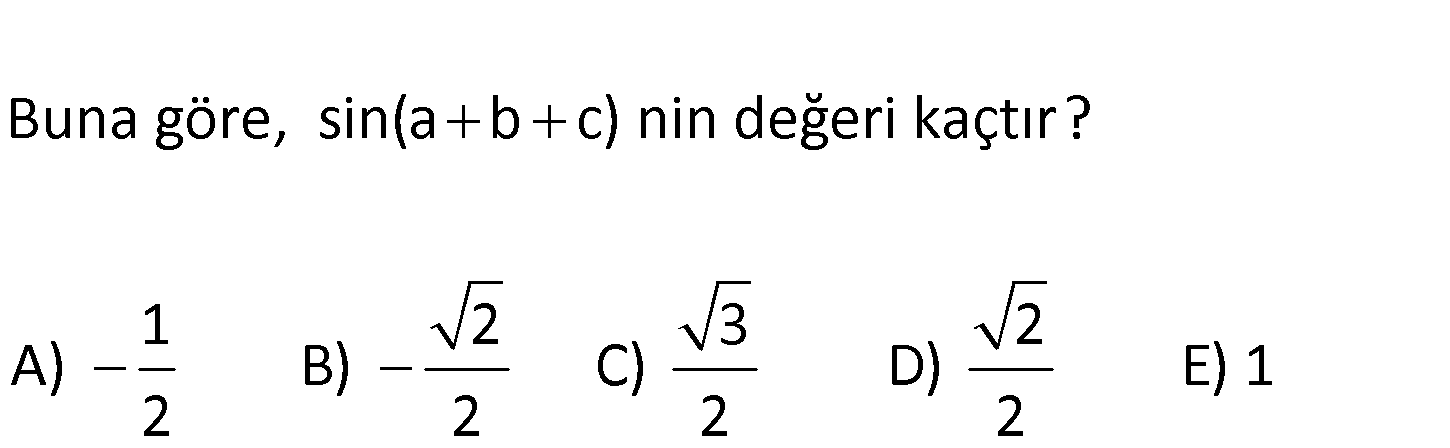

4.SORU
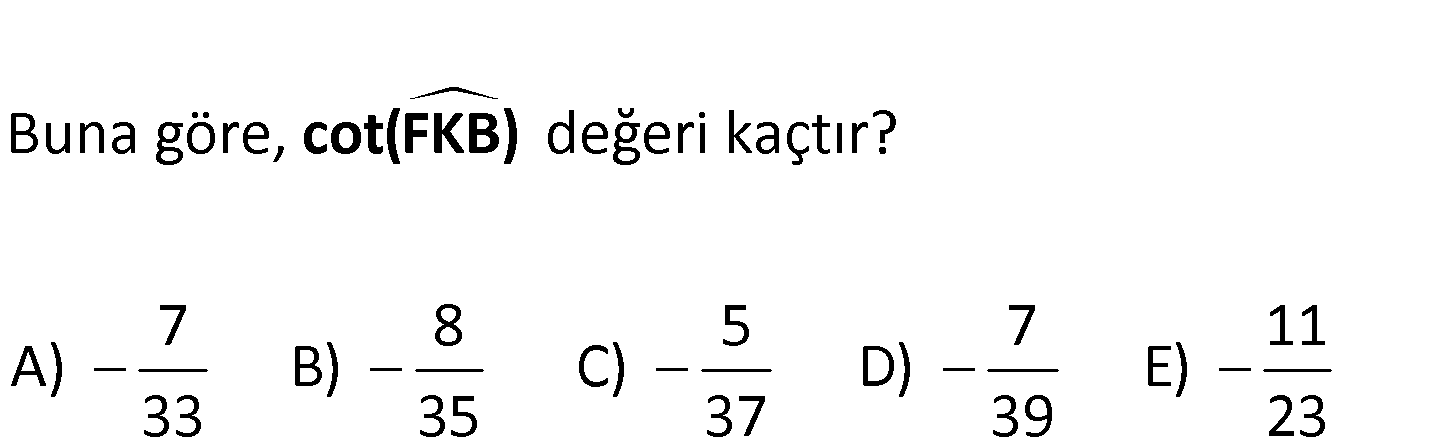
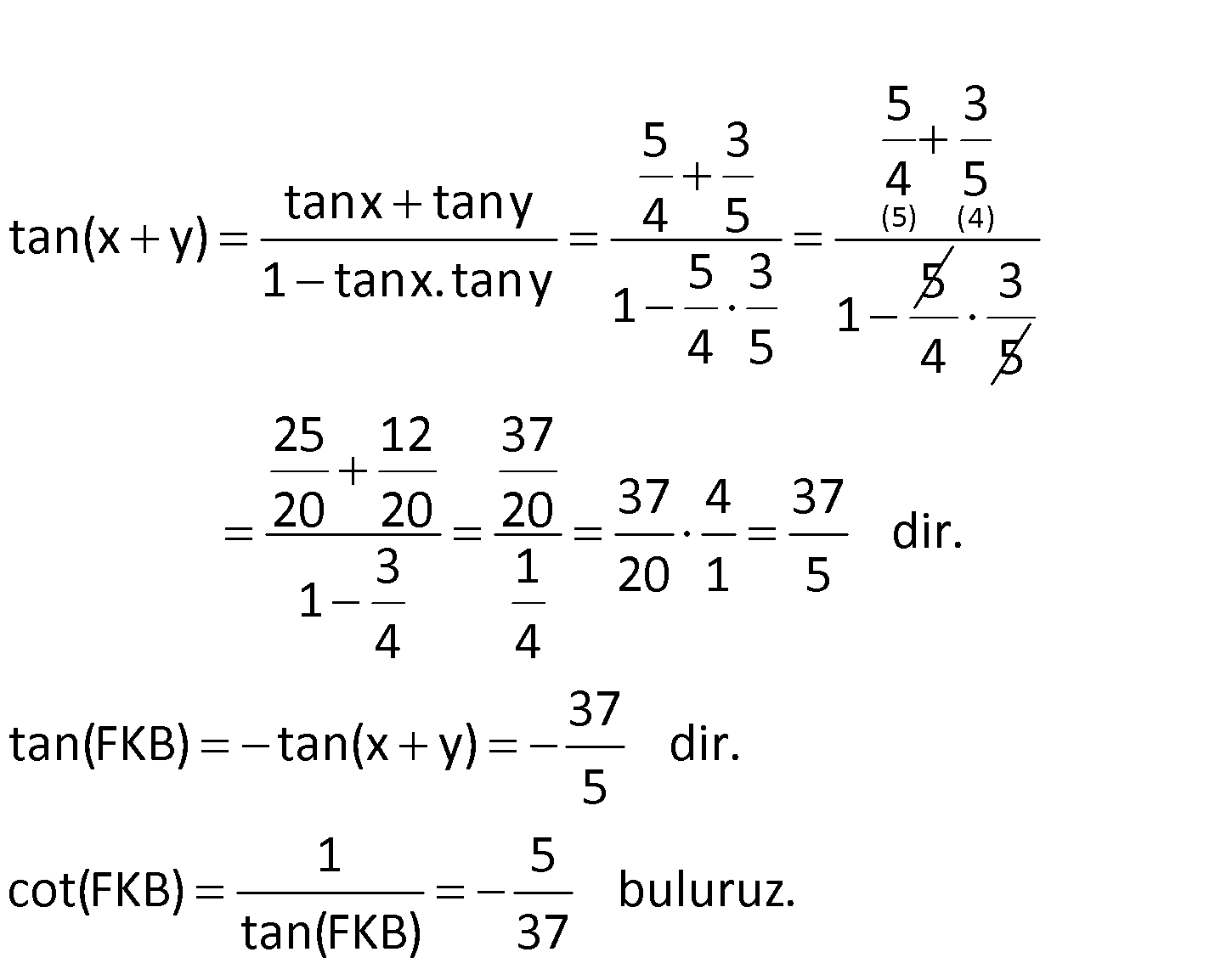
5.SORU


6.SORU

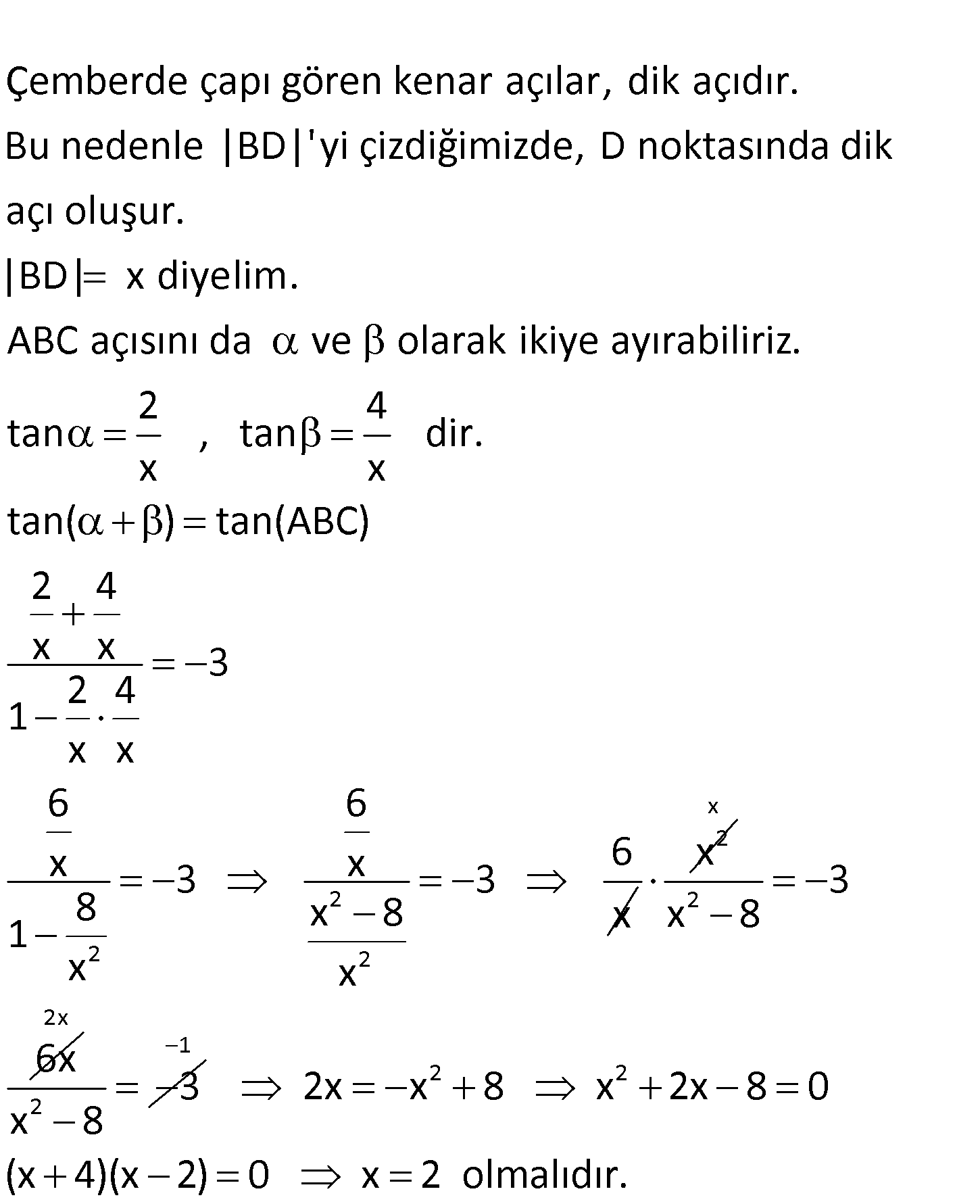
7.SORU
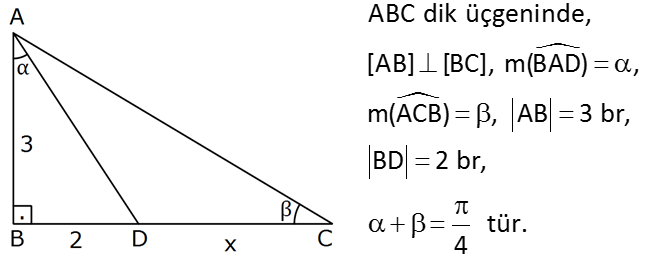

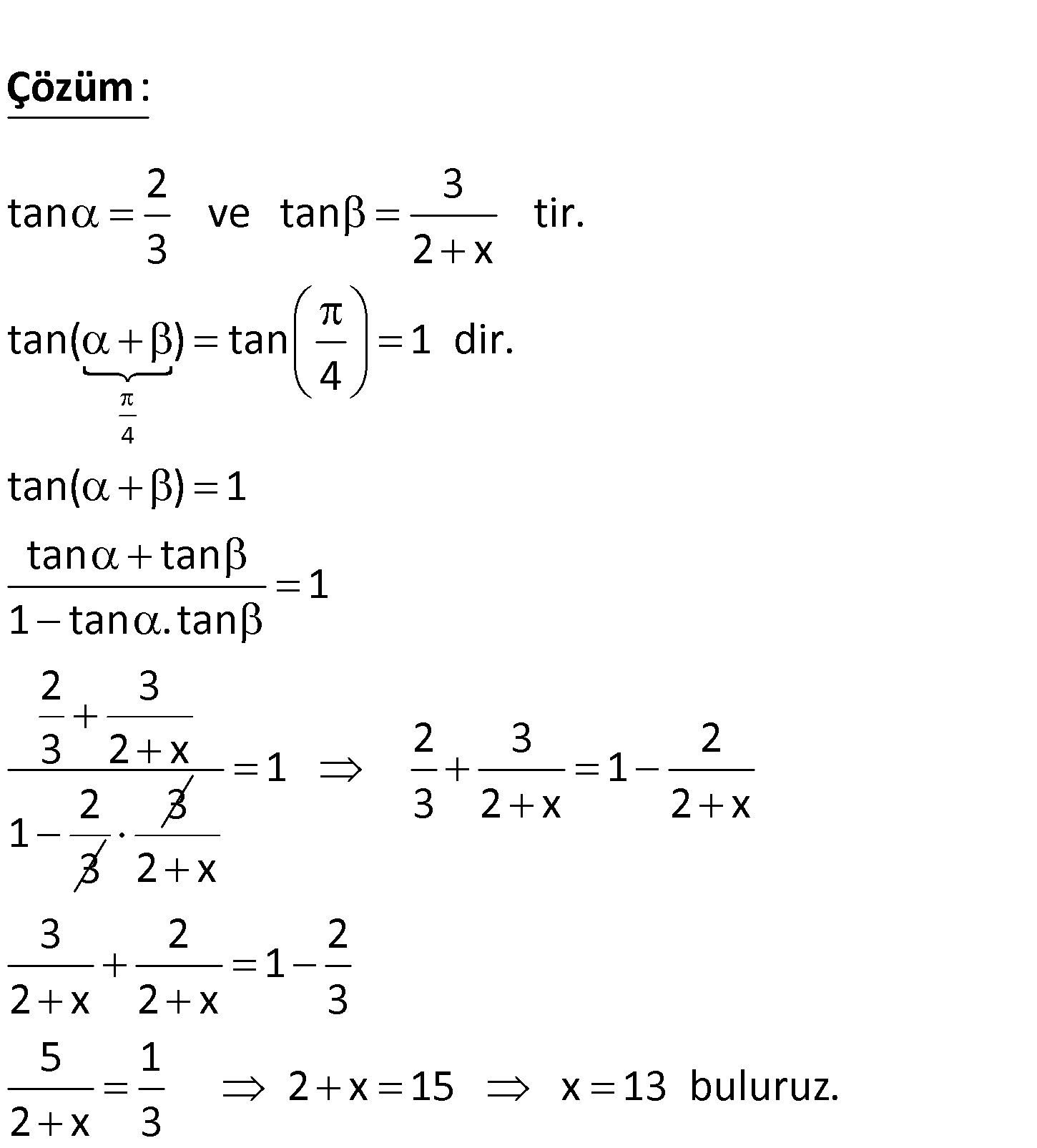
8.SORU

9.SORU
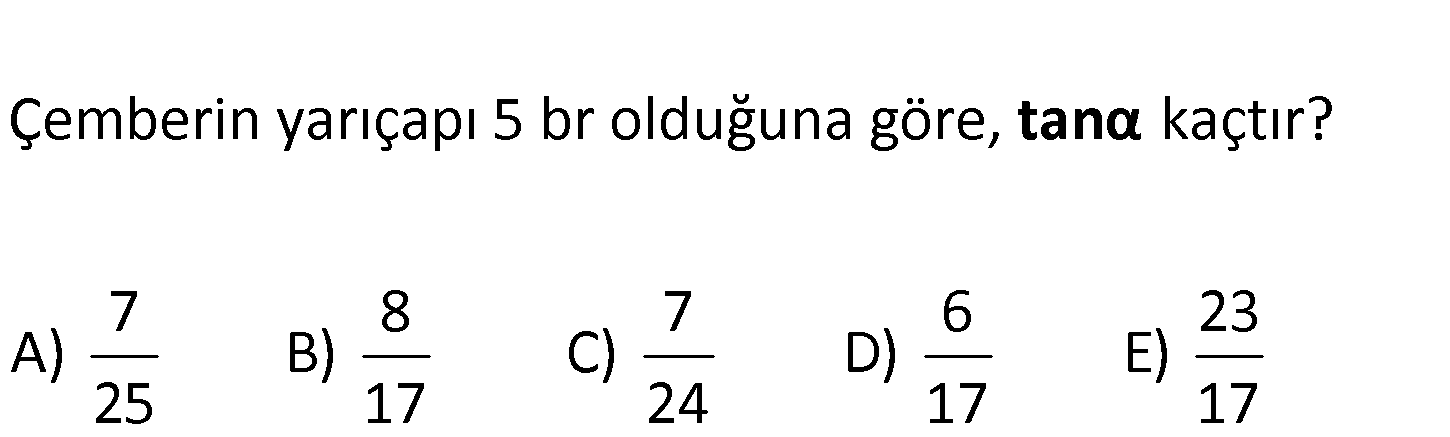
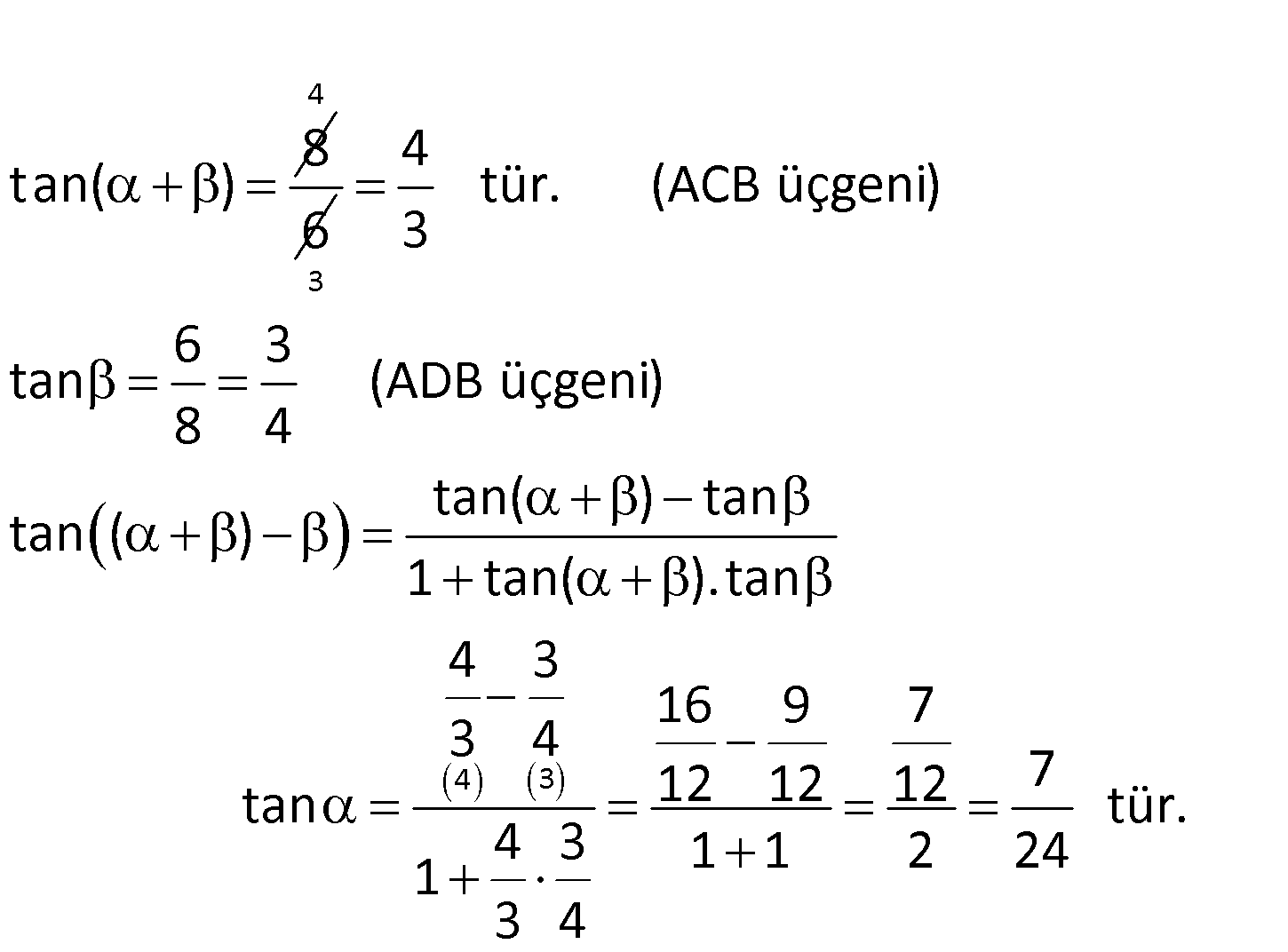
10.SORU


11.SORU
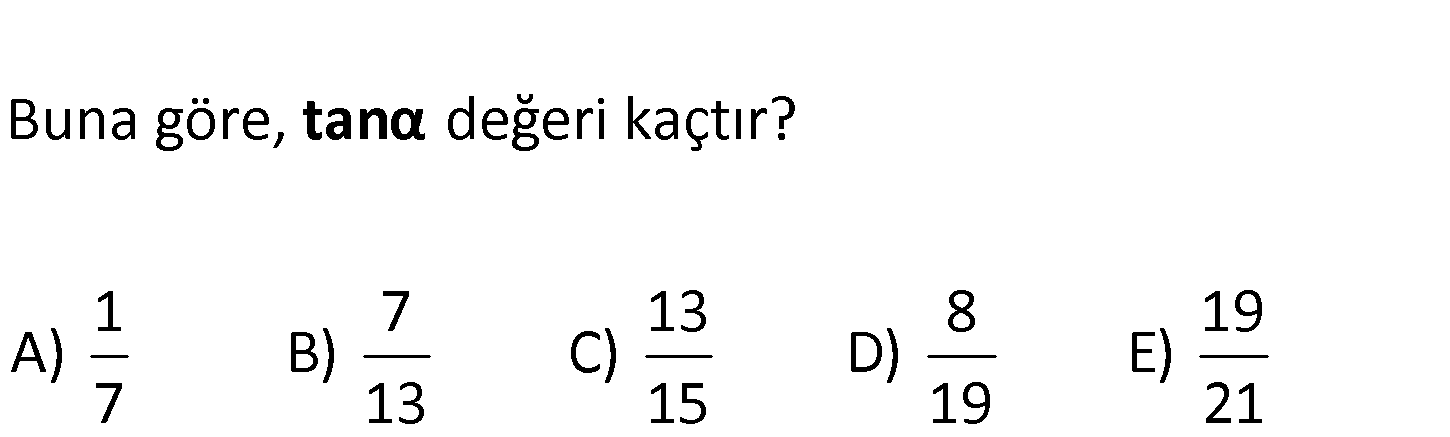
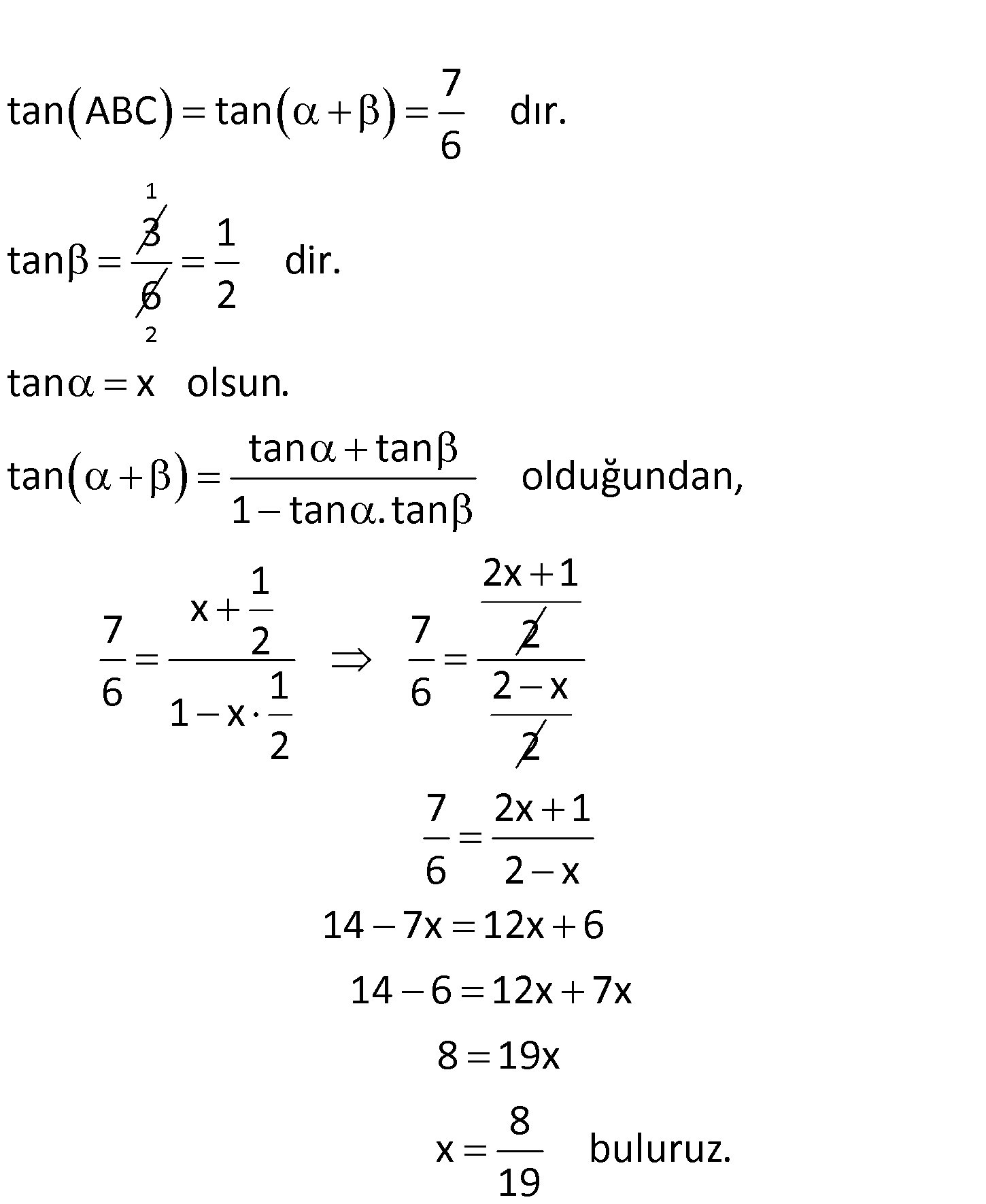
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
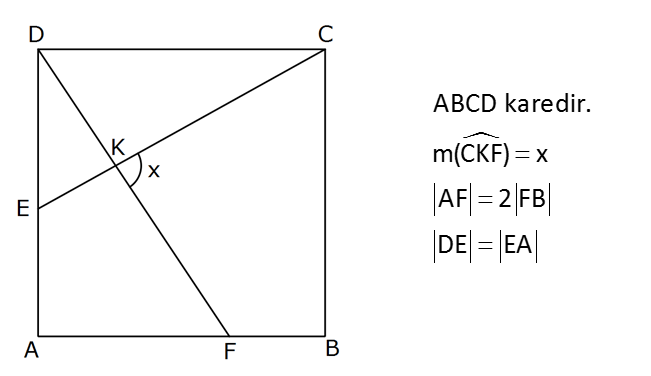
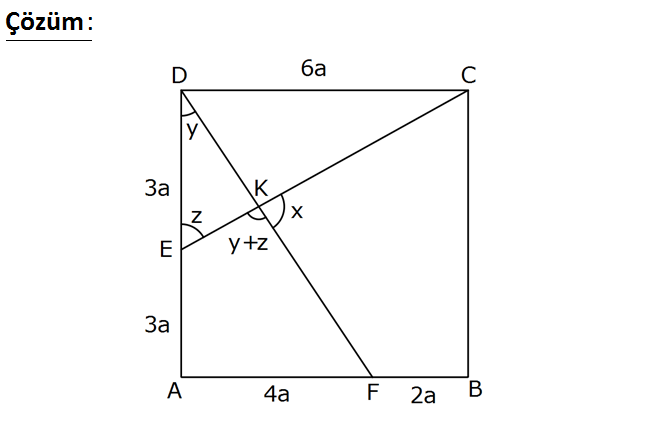
ABCD karedir. m(CKF) x AF 2 FB DE EA Yukarıdaki verilere göre, tanx değeri kaçtır? 1 1 A) B) C) 2 D) 4 E) 8 4 2 : Çözüm tanx tan(180 (y z)) tan(y z) 6 4 2 8 2 tany tanz 3 6 3 3 8 1 tany.tanz 6 4 2 1 1 1 2 3 6 3 3 5
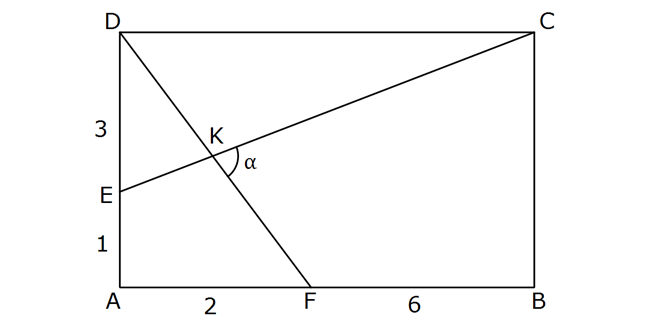
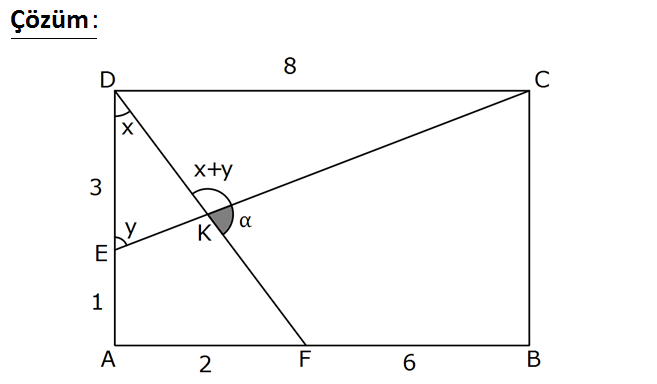
ABCD dikdörtgen, [CE] [DF] {K}, m(CKF) AE 1 br, ED 3 br, AF 2 br ve FB 6 br olduğuna göre, tanα nın değeri kaçtır? 17 19 21 23 25 A) B) C) D) E) 4 2 2 4 8 : Çözüm 2 1 tanx dir. (ADF üçgeni) 4 2 8 tany (CDE üçgeni) 3 tanx tany tan(x y) 1 tanx. ta 1 8 19 2 3 6 19 ny 1 8 1 2 1 2 3 3 19 tan tan(180 (x y)) tan(x y) buluruz. 2 18
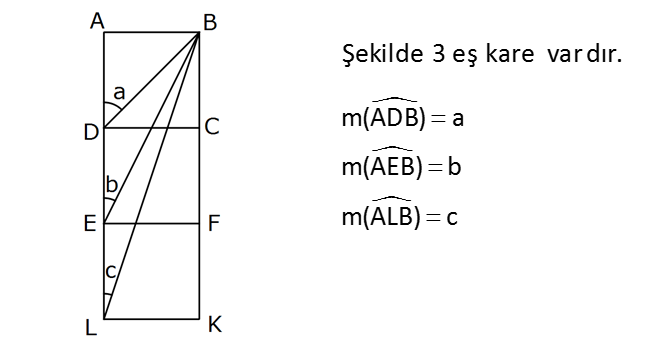
Şekilde 3 eş kare var dır. m(ADB) a m(AEB) b m(ALB) c Buna göre, sin(a b c) nin değeri kaçtır? 1 2 3 2 A) B) C) D) E) 1 2 2 2 2 1 1 tana 1 ; tanb ; tanc 2 3 1 3 1 tan(a b) 2 2 3 1 1 1 1 2 2 1 10 3 tan(a b c) 3 3 1 1 3 3 : Çözüm 0 tan90 dur. Buna göre a b c 90 dır. sin90 1 buluruz. 28
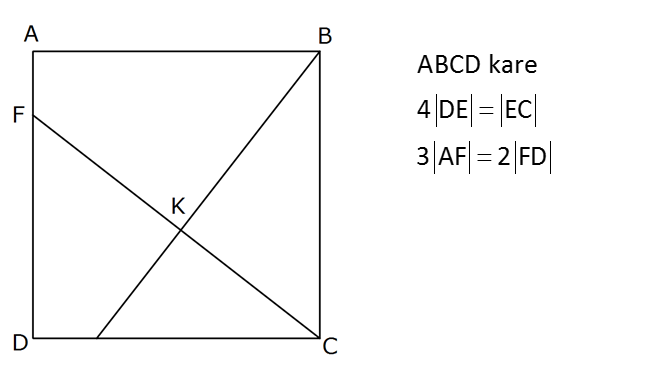
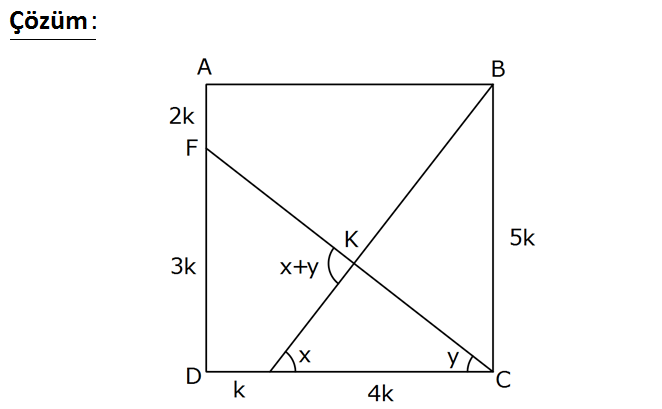
ABCD kare 4 DE EC 3 AF 2 FD Buna göre, değeri kaçtır? 7 8 5 7 11 A) B) C) D) E) 33 35 37 39 23 cot(FKB) : Çözüm (5) (4) 5 3 5 3 tanx tany 4 5 tan(x y) 4 5 1 tanx. tany 5 3 5 1 1 4 5 3 4 5 25 12 37 20 20 20 37 4 37 dir. 3 1 20 1 5 1 4 4 37 tan(FKB) tan(x y) dir. 5 1 5 cot(FKB) buluruz. tan(FKB) 37 45
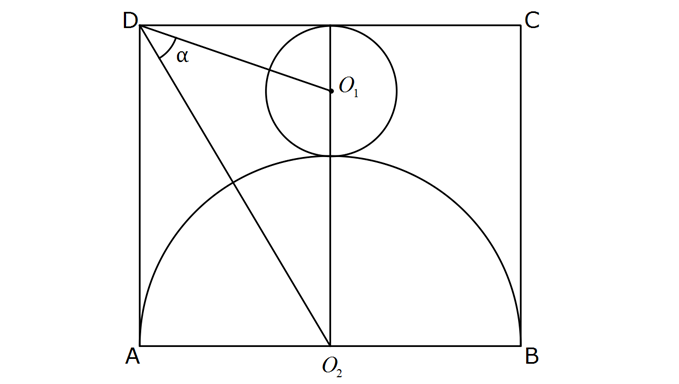
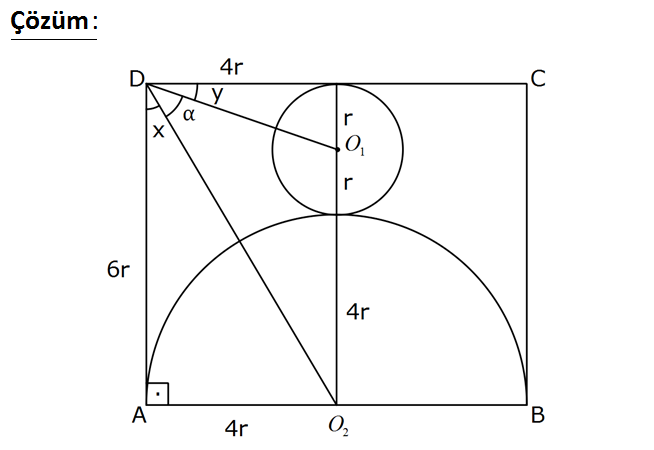
2 1 2 ABCD dikdörtgeninde O merkezli yarım dairenin alanı, O merkezli dairenin alanının 8 katıdır. m(O D 1 O ) olduğuna göre, nın değeri kaçtır? 5 5 11 13 17 A) B) C) D) E) 6 11 10 15 21 cotα : Çözüm 2 1 2 2 2 2 O merkezli yarım dairenin yarıçapı R, O merkezli dairenin yarıçapı r olsun. R 2 8 R 16r R r o (2) (3) 4r dir. x y 90 x y 90 tan(x y) tan(90 ) cot olur. 4 1 tanx tany 6 4 tan(x y) 1 tanx. tany 4 1 1 6 4 8 3 12 11 6 11 bulunur. 5 12 5 10 6 53
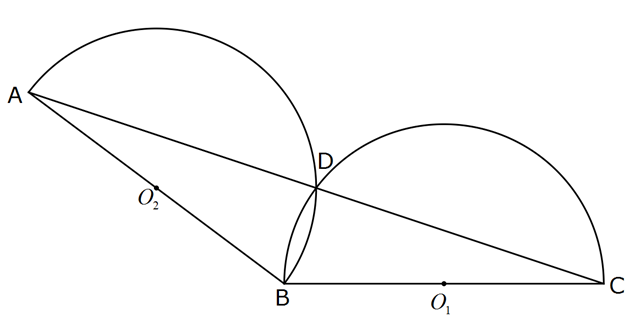
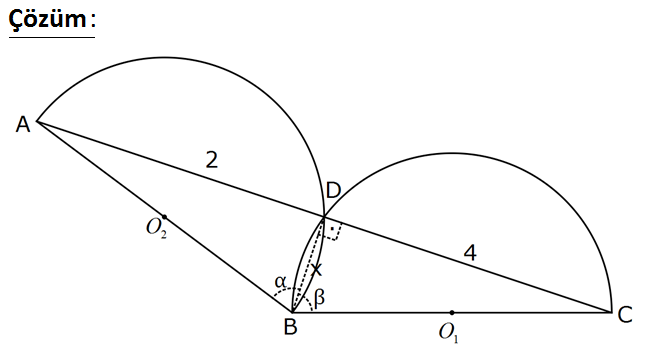
1 2 Şekilde O ve O merkezli yarım çemberler B ve D noktalarında kesişmiştir. AD 2 br , DC 4 br dir. tan(ABC) 3 olduğuna göre, B ile D noktaları arasındaki kaç birimdir? 1 3 5 A) B) 1 C) D)2 E) 2 2 2 en kısa mesafe : Çözüm Çemberde çapı gören kenar açılar, dik açıdır. Bu nedenle |BD|’yi çizdiğimizde, D noktasında dik açı 2 2 2 oluşur. |BD| x diyelim. ABC açısını da ve olarak ikiye ayırabiliriz. 2 4 tan , tan dir. x x tan( ) tan(ABC) 2 4 x x 3 2 4 1 x x 6 6 x x 6 3 3 8 x 8 x 1 x x 2 x x 2 3 x 8 6x 2x 2 3 x 8 1 2 2 2x x 8 x 2x 8 0 (x 4)(x 2) 0 x 2 olmalıdır. 56
ABC dik üçgeninde, [AB] [BC], m(BAD) , m(ACB) , AB 3 br, BD 2 br, tür. 4 Buna göre, kaç birimdir? A) 5 B) 12 C) 13 D)17 E) 21 DC = x 4 2 3 tan ve tan tir. 3 2 x tan( ) tan 1 dir. 4 tan( ) 1 tan tan 1 1 tan . t : an Çözüm 2 3 3 2 x 2 1 3 3 2 3 2 1 1 3 2 x 2 x 2 x 3 2 2 1 2 x 2 x 3 5 1 2 x 15 x 13 buluruz. 2 x 3 57
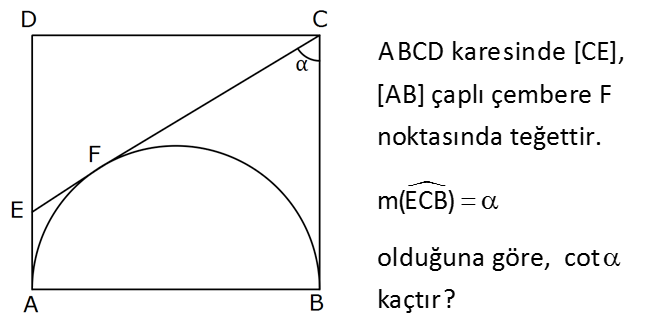
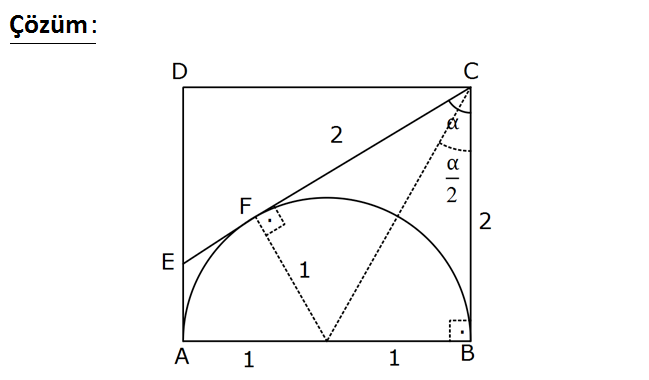
ABCD karesinde [CE], [AB] çaplı çembere F noktasında teğettir. m(ECB) olduğuna göre, cot kaçtır? 2 3 4 5 6 A) B) C) D) E) 3 4 5 6 7 : Çözüm Çemberin yarıçapı 1 birim olsun. Karenin bir kenarı 2 birim olur. C köşesinden çemberin merkezine çizilen doğru, açıortaydır. Buradan tan ‘nin değerini kullanarak, 2 cot değerine ulaşabiliriz. 1 tan 2 2 1 1 2 2 1 1 4 tan tür. 1 1 1 3 3 1 1 2 2 4 4 1 3 cot buluruz. tan 4 59
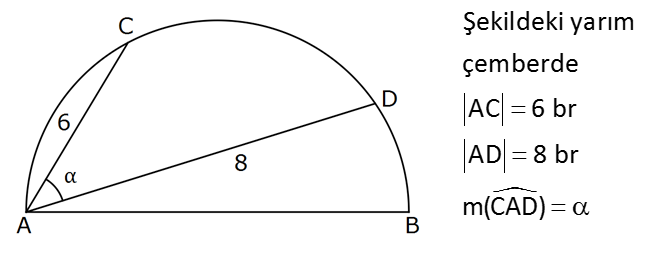
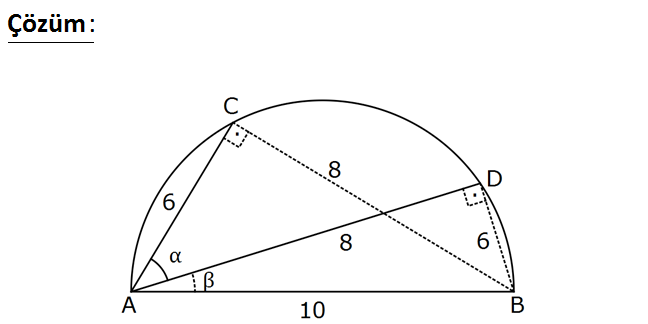
Şekildeki yarım çemberde AC 6 br AD 8 br m(CAD) Çemberin yarıçapı 5 br olduğuna göre, kaçtır? 7 8 7 6 23 A) B) C) D) E) 25 17 24 17 17 tanα : Çözüm 8 tan( ) 4 6 3 4 3 4 tür. (ACB üçgeni) 3 6 3 tan (ADB üçgeni) 8 4 tan( ) tan tan ( ) 1 tan( ). tan 4 3 16 9 7 3 4 12 12 12 7 tan tür. 4 3 1 1 2 24 1 3 4 63
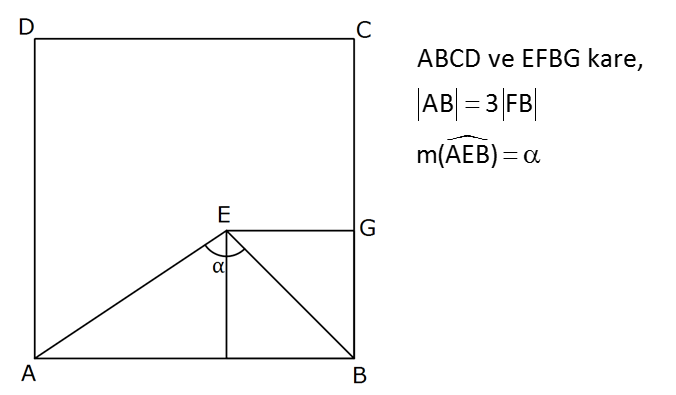
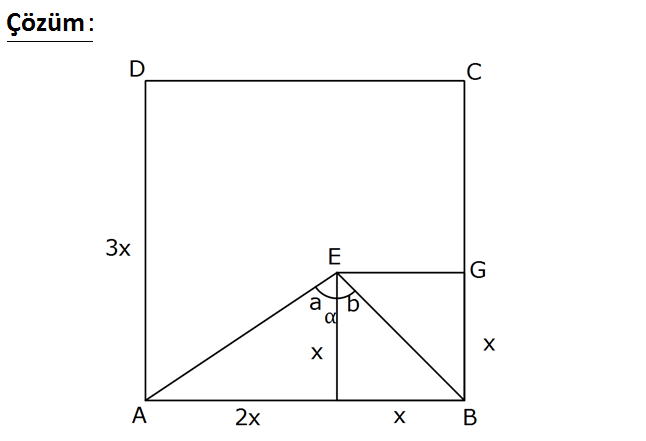
ABCD ve EFBG kare, AB 3 FB m(AEB) Buna göre, ifadesinin değeri kaçtır? 3 1 A) B) C) 2 D) 3 E) 4 2 2 tanα : Çözüm FB x dersek, AB 2x olur. 2x Buna göre; tana 2 dir. x x tanb 1 dir. x a b olduğundan; tan tan(a b) tana tanb 1- tana. tanb 2 1 3 3 buluruz. 1 2.1 1 67
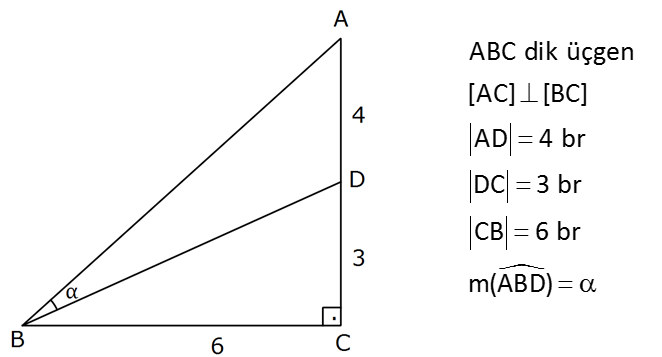
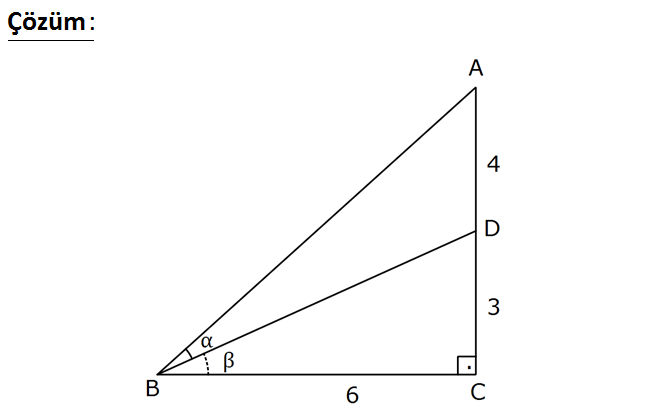
ABC dik üçgen [AC] [BC] AD 4 br DC 3 br CB 6 br m(ABD) Buna göre, değeri kaçtır? 1 7 13 8 19 A) B) C) D) E) 7 13 15 19 21 tanα : Çözüm 7 tan ABC tan dır. 6 3 tan 1 6 2 1 dir. 2 tan x olsun. tan tan tan olduğundan, 1 tan . tan 1 2x 1 x 7 2 7 2 6 1 6 1 x 2 2 x 2 7 2x 1 6 2 x 14 7x 12x 6 14 6 12x 7x 8 19x 8 x buluruz. 19 72


teşekkürler.