Soru Sor sayfası kullanılarak Rasyonel Sayıların Sıralanması konusu altında Paylar eşitse ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
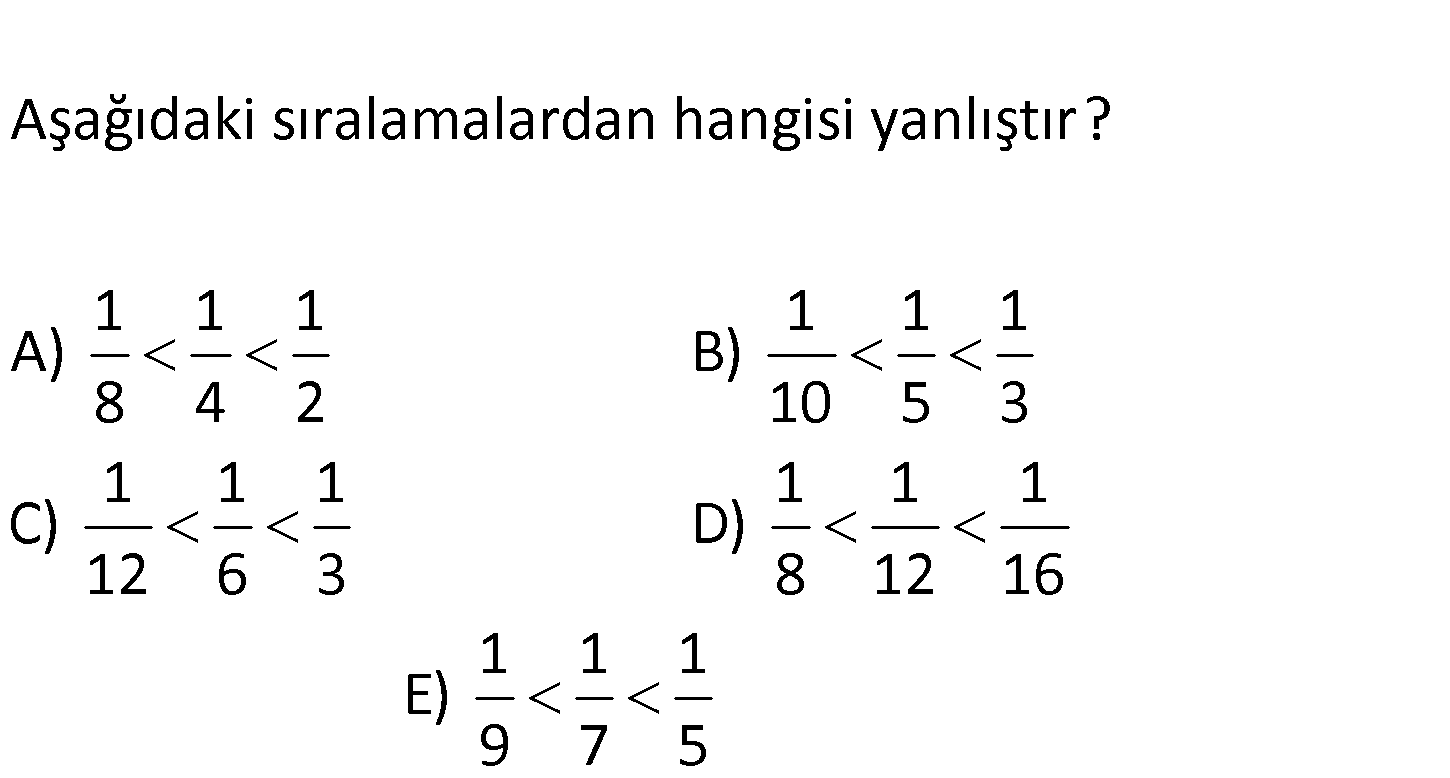

2.SORU
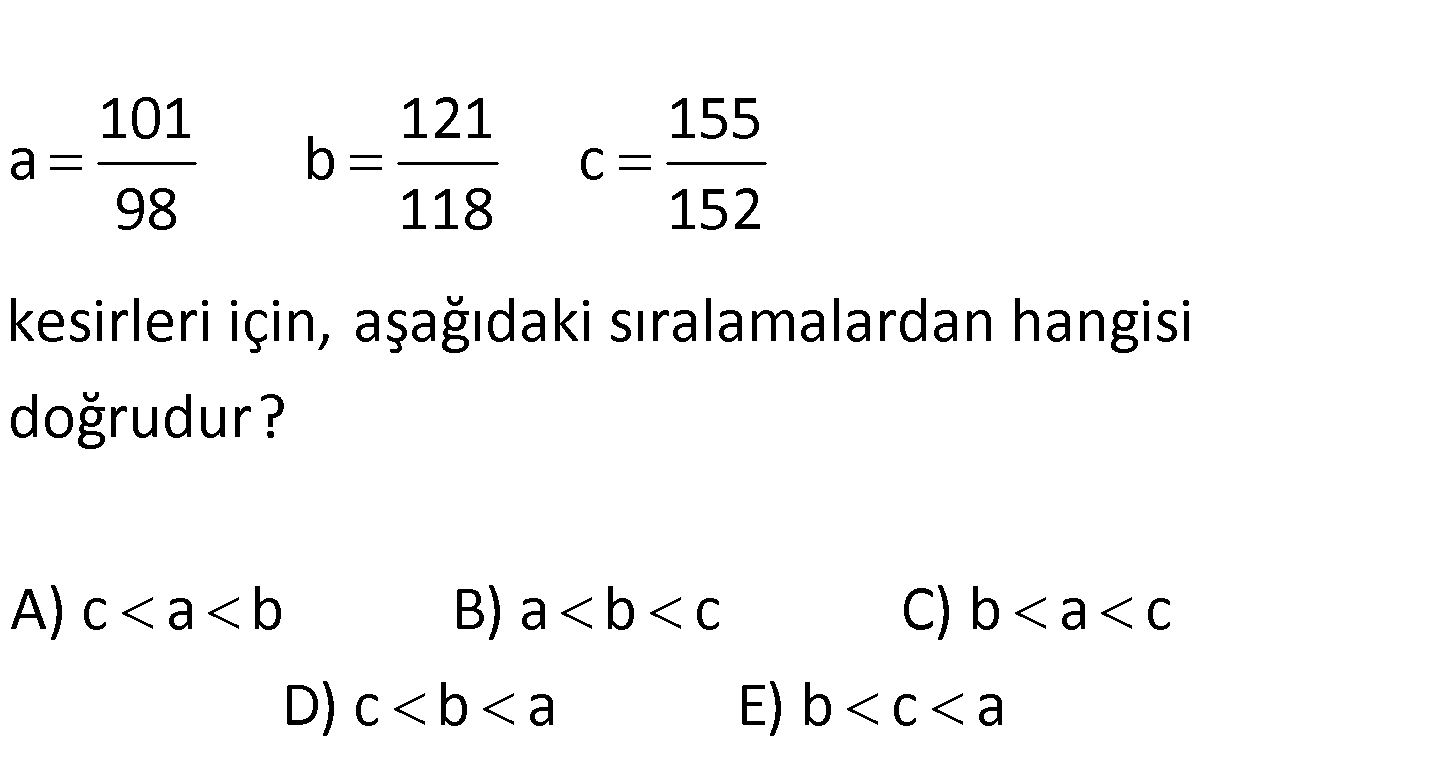

3.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
5 2 x kesri bileşik kesir olduğuna göre, x yerine gelebi – lecek tam sayıların toplamı kaçtır? A) 20 B) 21 C) 22 D) 23 E) 24 www.matematikkolay.net a a a Not : bileşik kesir ise 1 veya 1 dir. b b b 1.durum Payda pozitif ise x 2 : ise 5 1 2 x Çözüm 5 2 x 3 x 3 x x 3 tür. 3, 2 2.durum Payda negatif ise x 2 ise 5 1 2 x Negatif paydadan dolayı eşitsizlik 5 2 x yön değiştirdi. 5 x 2 7 x x 7 dir. 2,7 Bu durumlara uygun x tam sayıları n toplamı; 3 2 1 0 1 3 4 5 6 7 20 dir. 3
x bir tamsayı olmak üzere, 2x 3 x 9 ve x 9 2x 3 ifadeleri tamsayı olduğuna göre, x ‘in alab ileceği değerlerin toplamı kaçtır? A) 14 B) 12 C) 10 D) 9 E) 8 www.matematikkolay.net 2x 3 x 9 2x 3 ve tam sayı ise 1 dir. x 9 2x 3 x 9 1.Durum: 2x 3 1 2x 3 x 9 x 9 2x x 9 3 x 12 d . : ir Çözüm 2.Durum: 2x 3 1 2x 3 x 9 x 9 2x x 9 3 3x 6 6 x 2 dir. 3 12 2 12 2 10 bulunur. 10
1 1 3 1 x 1 ifadesini tanımsız yapan x değerlerinin toplamı kaçtır? A) 3 B) 1 C) 1 D) 3 E) 5 www.matematikkolay.net Paydayı 0 yapan x değeri, kesri tanımsız yapar. 1 1 x 1 x 1 olamaz. 3 1 x 1 İşlem : leri y Çözüm apmaya devam edelim. 1 1 1 x 1 1 1 1 1 3 x 1 3 x 2 x 2 1 x 1 x 1 x 1 x 2 olamaz. İki değer bulduk. Bunları toplayalım. 1 2 1 buluruz. 13

