Soru Sor sayfası kullanılarak Rasyonel Sayılarda Dört İşlem konusu altında Sonsuza giden kesirler ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
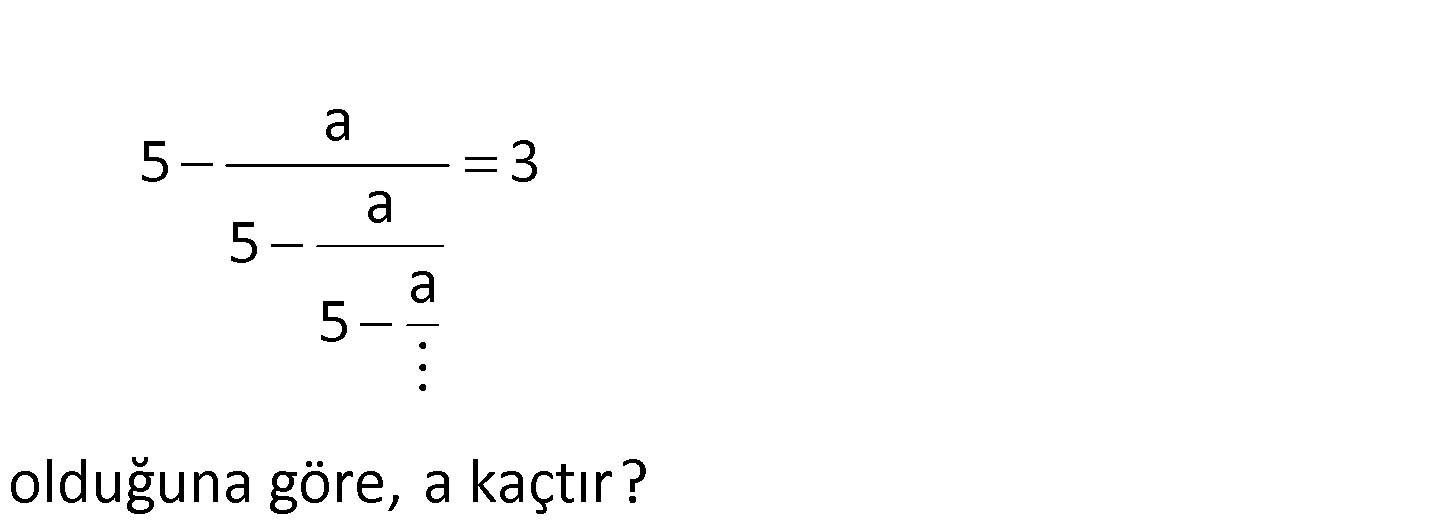

2.SORU


3.SORU


4.SORU


5.SORU

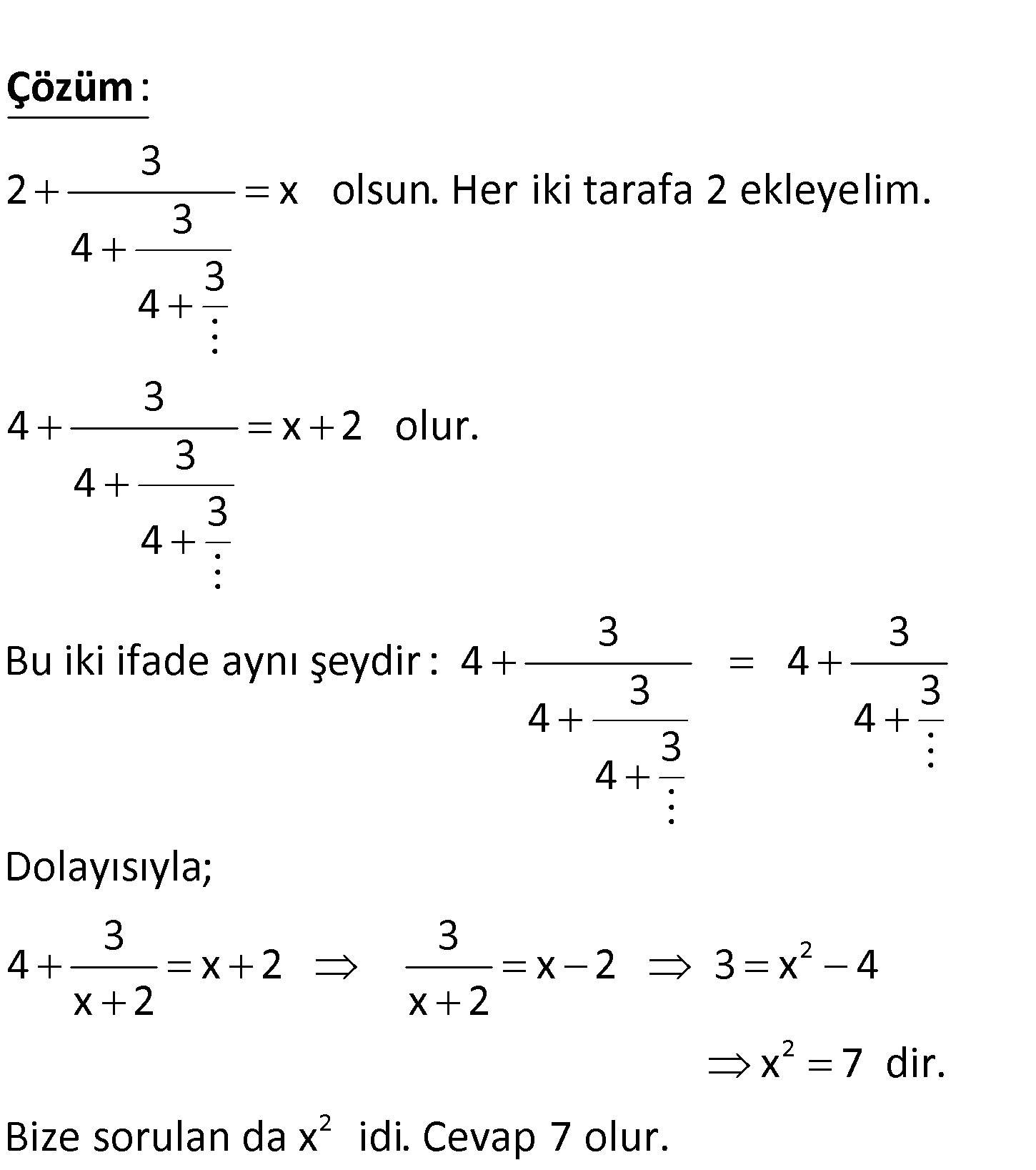
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
a 5 3 a 5 a 5 olduğuna göre, a kaçtır? www.matematikkolay.net Aşağdaki üç ifade de sonsuza kadar uzadığı için, 3’ü de aynı ifade olarak kabul edilir. : Bu ne Çözüm denle hepsi 3′ e eşit olacaktır. a a a 5 5 5 a a 5 5 a 5 Bu sebeple ; a a 5 3 ifadesini 5 3 şeklinde a 3 5 a 5 sadeleştirip, kolaylıkla çözebiliriz. a a 5 3 2 a 6 dır. 3 3 17
12 işleminin sonucu kaçtır? 6 1 6 1 6 1 A) 2 B) 3 C) 4 D) 6 E) 12 www.matematikkolay.net 12 6 1 6 1 6 1 Kutu içerisine aldığımız kısmın sonucu x olsun. 6 1 x 6 1 6 1 Tekrar eden kısım : da Çözüm 2 2 x’ e eşit olur. 6 1 x x 6 x 1 6 x x x x x 6 0 (x 3)(x 2) 0 x 3 ve x 2 bulunur. Soruda verilen ifadede hiç negatif sayı olmadığından sonuç negatif olamaz. O halde yalnız 3’ü alırız. 12 4 bulunur. 3 21
www.matematikkolay.net 25 işleminin sonucu kaçtır? 25 10 25 10 25 10 A) 5 B) 10 C) 20 D) 25 E) 50 25 25 10 25 10 25 10 Sürekli tekrar eden kısmı kutu içerisine alalım ve bunun sonucu x olsun. 10 : Çözüm 25 x ise; 25 10 25 10 Sürekli devam eden benzer kısma da x diyebiliriz. O halde; 25 10 x şeklinde bir denklem kurabiliriz. x (Bu aşamada x ‘in 5 olduğunu görebiliriz. Görmedi – ğimizi düşünerek işleme2 2 2 devam ediyoruz) 10x 25 x 10 x 25 x x 0 x 10x 25 0 (x 5) x 5 tir. Kutu içerisindeki ifade 5 ise; sorudaki ifade 25 25 5 buluruz. x 5 www.matematikkolay.net 22
20 3 20 1 20 1 işleminin sonucu kaçtır? www.matematikkolay.net 2 1 20 3 x 20 1 20 1 20 1 x 2 tür. 20 1 20 1 Sürekli tekrar eden ifade x 2 ise , payda kısm : ı Çözüm 5 4 nda da aynı ifade yerine x 2 yazabiliriz. Yani; 20 1 x 2 olur. Bunu çözelim. x 2 20 x 3 20 (x -2)(x -3) x 7 buluruz. x 2 49
3 2 3 4 3 4 ifadesinin karesi kaçtır? www.matematikkolay.net 3 2 x olsun. Her iki tarafa 2 ekleyelim. 3 4 3 4 3 4 x 2 olur. 3 4 3 4 Bu iki ifade ay : nı şe Çözüm 2 2 2 3 3 ydir : 4 4 3 3 4 4 3 4 Dolayısıyla; 3 3 4 x 2 x 2 3 x 4 x 2 x 2 x 7 dir. Bize sorulan da x idi. Cevap 7 olur. 61

