
Matematik Diline Çevirme
Verilen problemi anladıktan sonra bilinmeyenleri x, y, a, b gibi sembollerle ifade etmeye matematik diline çevirme denir.
Örnek:

Örnek:

Çözüm:

Örnek:

Çözüm:

Not: Sayı problemlerinde bilinmeyen sayısını mümkün olduğu kadar az tutmak, çözümü kolaylaştırır.
Örnek:

Çözüm:

Örnek:

Çözüm:

Örnek:

Çözüm:
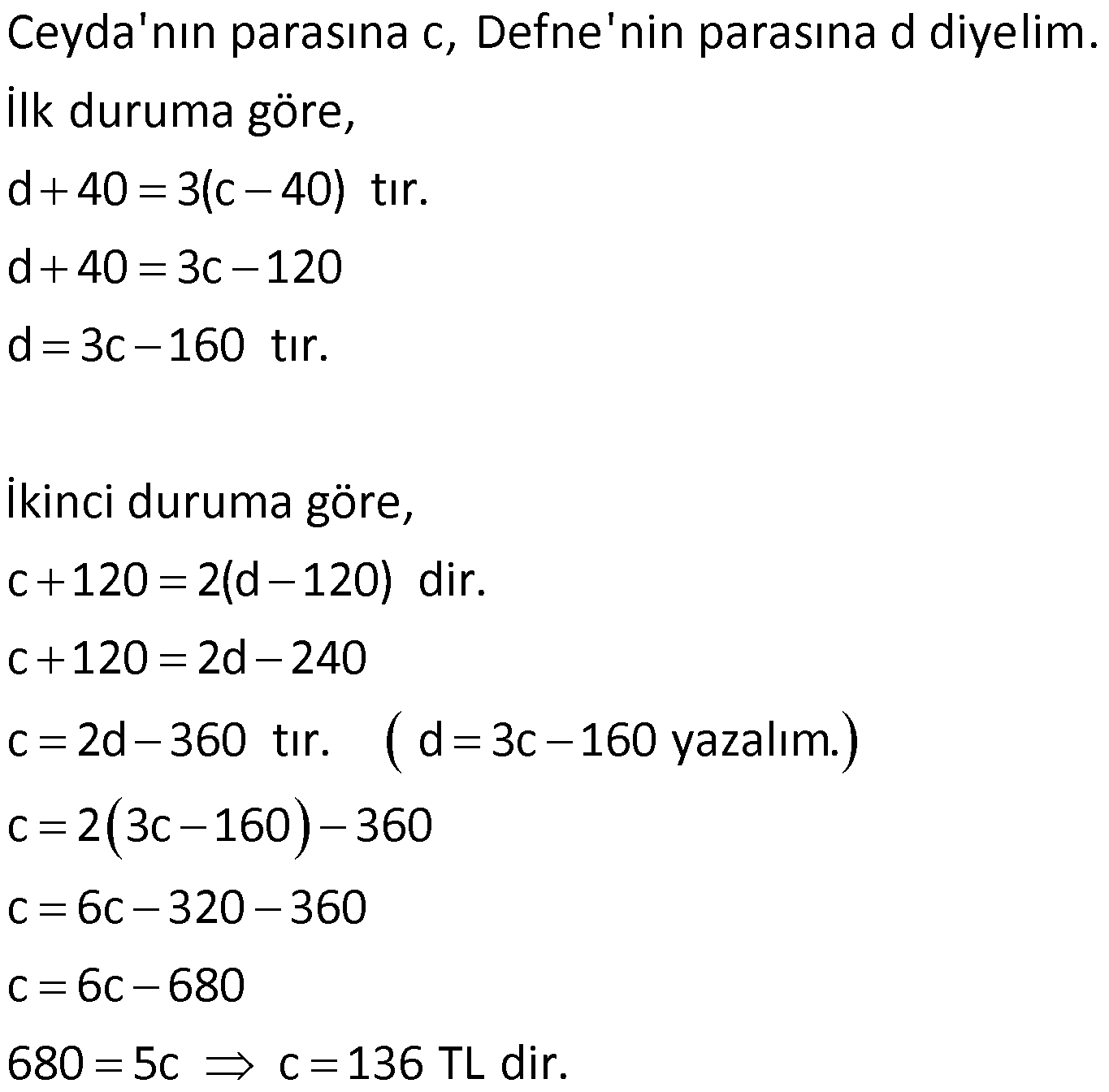
Örnek:

Çözüm:

Örnek:

Çözüm:

Örnek:

Çözüm:

Örnek:

Çözüm:

Çözümlü Sorular veya Daha Fazlası için Tıkla
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)SAYI PROBLEMLERİ KONU ANLATIMI www.matematikkolay.net Matematik Diline Çevirme Verilen problemi anladıktan sonra bilinmeyenleri x, y, a, b gibi sembollerle ifade etmeye matematik diline çevirme denir. Örnek: Bir sayının 3 fazlası : x 3 x 2 Bir sayının 2 fazlasının yarısının 4 fazlası : 4 2 Bir sayının 3 fazlasının 7 katı Recep ile Fatih’in yaşları farkı 8 dir : x y 8 Bir sayının karekökü, karesinden büyüktür: 2 2 2 x x İki sayının kareleri toplamı 25 tir: x y 25 Örnek: Toplamları 25 olan iki sayıdan büyüğü, küçüğünün 3 katından 1 fazladır. Buna göre, küçük sayı kaçtır? Çözüm: Küçük sayı x olsun. Büyük sayı 3x 1 olur. İkisinin toplamı 25 ise, x 3x 1 25 4x 24 x 6 dır (Küçük Sayı). Örnek: Ardışık iki çift sayının toplamları 30 dur. O halde büyük sayı kaçtır? Çözüm: Büyük sayı x olsun. Küçük sayı x 2 olur. İkisinin toplamı 30 ise, x x 2 30 2x 32 x 16 dır Büyük Sayı . Not: Sayı problemlerinde bilinmeyen sayısını mümkün olduğu kadar az tutmak, çözümü kolaylaştırır. Örnek: Bir sınıfta Ayşe’nin kız arkadaşları sayısı, erkek arka – daşlarının sayısının 2 katıdır. Hüseyin’in erkek arkadaşlarının sayısı ise, kız arkadaşlarının sayısından 14 eksiktir. O halde bu sınıfın mevcudu kaçtır? Çözüm: Erkeklerin sayısı x olsun. Ayşe’nin erkek arkadaşlarının sayısı da x olur. Ayşe’nin kız arkadaşlarının sayısı ise 2x olur. Ayşe’ yi de dahil edersek, bu sınıfta 2x 1 kız var dır. Hüseyin’in erkek arkadaşlar ının sayısı x 1 dir. kız arkadaşlarının sayısı da 2x 1 dir. Aradaki fark 14 ise, 2x 1 x 1 14 2x 1 x 1 14 x 2 14 x 12 dir. Sınıf mevcudu x 2x 1 12 24 1 12 25 37 dir. Örnek: Bir şişede başlangıçta bir miktar su vardır. Şişeden 3 bardak su alınırsa, şişenin yarısı kadar su kalmış oluyor; 2 bardak su eklenirse şişe tamamen doluyor. O halde, başlangıçta kaç bardak su var dır? Çözüm: Başlangıçtaki su miktarına a lt diyelim. Bir bardağın aldığı su miktarına b lt diyelim. a 3b Şişenin yarısı a 2b Şişenin tamamı ise a 2b değeri a 3b ‘nin 2 katıdır. a 2b 2 a 3b a 2b 2a 6b 8b a dır. Başlangıçta 8 bardak su var dır. www.matematikkolay.net Örnek: Ceyda, Defne’ye 40 TL verirse, Defne’nin parası Ceyda’nın parasının 3 katı oluyor. Eğer, Defne Ceyda’ya 120 lira verirse, Ceyda’nın parası Defne’ nin 2 katı oluyor. Buna göre, başlangıçta Ceyda’nın parası kaç TL dir? Çözüm: Ceyda’nın parasına c, Defne’nin parasına d diyelim. İlk duruma göre, d 40 3(c 40) tır. d 40 3c 120 d 3c 160 tır. İkinci duruma göre, c 120 2(d 120) dir. c 120 2d 240 c 2d 360 tır. d 3c 160 yazalım. c 2 3c 160 360 c 6c 320 360 c 6c 680 680 5c c 136 TL dir. Örnek: Bir sınıftaki sıralara 2’şerli oturulursa 5 öğrenci ayak – ta kalıyor. Eğer 3’erli otururlarsa 3 sıra boş kalıyor Oturulan sıralarda herkes 3’erli oturuyor . Buna göre, sınıfta kaç öğrenci var dır? Çözüm: 14 Sıra sayısına x diyelim. İlk duruma göre öğrenci sayısı 2x 5 tir. İkinci duruma göre öğrenci sayısı 3 x 3 tür. Bu ikisini birbirine eşitleyelim. 2x 5 3x 9 14 x tir. Öğrenci sayısı 2 x 5 28 5 33 tür. Örnek: Elif, en az birer tane A ve B markalarından sakız alacaktır. A marka sakızın fiyatı 50 kuruş, B marka sakızın fiyatı ise 75 kuruştur. Elif ‘in 7 lirası olduğuna göre, parasının tamamıyla en fazla kaç sakız alabilir? Çözüm: 7 lira 700 kuruştur. 50.A 75.B 700 eşitliği sağlanmalıdır. Her tarafı 25’e bölelim. 2A 3B 28 olur. En fazla sakız için, B değerini düşük tutmalıyız. B 1 dersek 2A 3 28 2A 25 A tam sayı değil. B 2 dersek 2A 6 28 2A 22 A 11 olur. O halde, A B 11 2 13 tür (En fazla). Örnek: Bir tırtıl ağaca tırmanırken günde 3 metre ileri çık – makta, sonra 2 metre aşağı inmektedir. 30 metrelik bir ağacın en yüksek noktasına ilk defa kaçıncı gün ulaşır? Çözüm: Bir günde 3 2 1 metre ilerler. 30 30 metrelik ağacın tepesine 30 gün sonra ulaşır, 1 dersek hatalı olur. Çünkü daha önceden buraya ulaşmıştır. 26.günün sonunu düşünelim. 26.1 26 metre yukarıdadır. 27.gün 2 6 3 29 metreye çıkar. Sonra 29 2 27 metreye geri iner. 28.gün 27 3 30 metreye çıkar. Sonra geri iner ama 30. metreye bir kere ulaşmıştır artık. O yüzden cevap 28. www.matematikkolay.net Örnek: Hilmi, ilk gün 12 sayfa kitap okumuştur. Sonraki günlerde ise, bir önceki güne göre 2 sayfa daha fazla okumuştur. Bu şekilde ilerledikten sonra araya yazılılar girdiği için, bu günlerde her gün 15 sayfa kitap okumuştur ve kitap bitmiştir. 15 sayfa kitap okuduğu gün sayısı 6 olduğuna göre, 300 sayfalık kitabı kaç günde bitirmiştir? Çözüm: 1.gün 2.gün 3.gün n.gün n İlk gün Son Gün 2 15.6 90 300 90 210 sayfayı yazılılardan önce okumuştur. 12 12 2 12 4 … 12 (n 1).2 210 dur. Terim Sayısı. Ortalama 210 12 12 (n 1).2 n 210 2 2 n 10.Kas 4 2n 2 210 2 22 2n n 210 2 n (11 n) 210 n 10 dur. O halde, tüm kitap 10 6 16 günde bitmiştir.


güzel anlatılmış
çok iyi anlatmışsınız hocam 🙂
hocam projem vardı bu derste anlatım çok azdı sadece soru çözulmus uzun uzun keske konuyu anlatsaydınız
müthiş… elinize sağlık
hocam öncelikle ellerinize sağlık, şuanlık öğrenmişim gibi görünüyor umarım sorularda da bu bilgimi kullanabilirim tekrardan çok teşekkürler:)
teşekkür ederim hocam.çok işime yaradı.