Permütasyon Konu Anlatımı

Tekrarlı Permütasyon

n tane nesnenin $\displaystyle {{n}_{1}}$ tanesi 1. çeşitten, $\displaystyle {{n}_{2}}$ tanesi 2. çeşitten, … , $\displaystyle {{n}_{r}}$ tanesi de r. çeşitten olsun.
$\displaystyle n={{n}_{1}}+{{n}_{2}}+...+{{n}_{r}}$ olmak üzere bu n tane nesnenin n li permütasyonlarının sayısı, $\displaystyle \frac{{n!}}{{{{n}_{1}}!.{{n}_{2}}!...{{n}_{r}}!}}$ dir.

Örnek:

ANNE kelimesinin harflerinin yerleri değiştirilerek anlamlı ya da anlamsız dört harfli kaç kelime yazılabilir?

Çözüm

ANNE kelimesinde 4 harf vardır ama 2 harf aynıdır. Dolayısıyla $\displaystyle \frac{{4!}}{{2!}}=\frac{{24}}{2}=12$ farklı kelime yazılabilir.

Alıştırma 12

Çözüm

Alıştırma 13

Çözüm

Alıştırma 14

Çözüm

Alıştırma 15

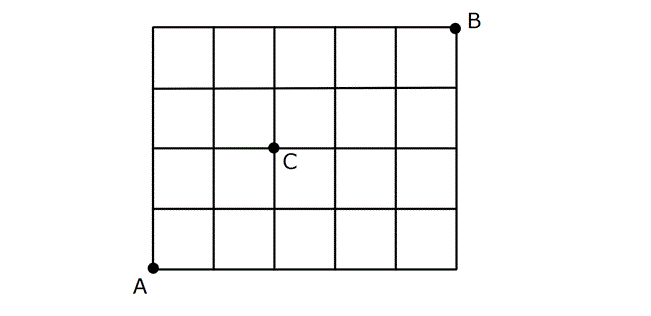
Çözüm

Alıştırma 16 (Ayraç Yöntemi)

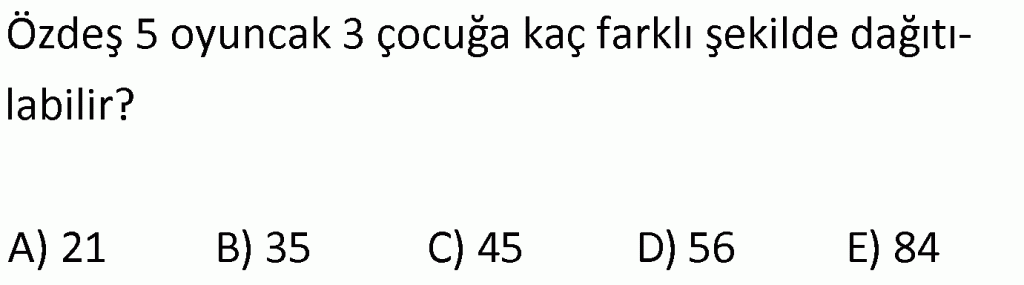
Çözüm

Alıştırma 17 (Ayraç Yöntemi)

Çözüm

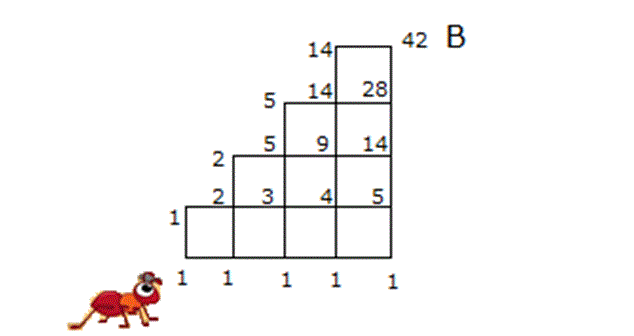
Alıştırma 18 (Şekilden Toplayarak Sayma)

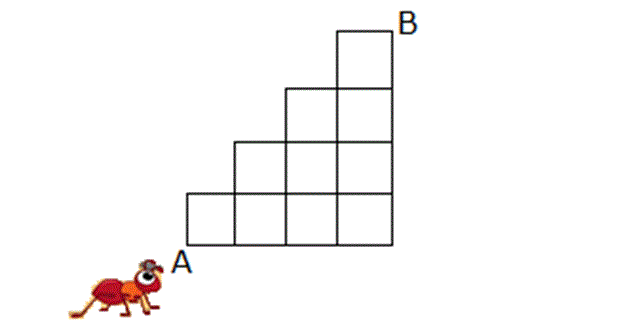
Çözüm

Dairesel (Dönel) Permütasyon (Fen Liseleri için)

n tane farklı elemanın dönel (dairesel) sıralamasına, n elemanın dönel (dairesel) sıralaması denir. Elemanlardan biri sabit tutularak n elemanın dönel (dairesel) sıralamalarının sayısı (n – 1)! ile bulunur.

Örnek:

Anne, Baba ve 3 çocuk yuvarlak bir masa etrafında kaç farklı şekilde oturabilirler?

Çözüm

Aile 5 kişiden oluşmaktadır. (5-1)!=4!=24 farklı şekilde yuvarlak masaya otururlar.

Örnek:

Bu sefer, 3 çocuk yanyana olmak koşuluyla yuvarlak bir masa etrafına kaç farklı şekilde oturabilirler?

Çözüm

3 çocuğu tek bir kişi olarak düşüneceğiz. Anne, Baba ve Çocuk Grubu yani 3 kişi yuvarlak bir masaya (3-1)!=2! şekilde oturur.

3 çocuk da kendi arasında 3! şekilde yer değiştirebilir.

O halde,

2!.3!=2.6=12 farklı şekilde oturabilirler.

Halka

n tane farklı eleman bir halkada $\displaystyle \frac{{(n-1)!}}{2}$ farklı şekilde sıralanır.

Örnek:

6 farklı anahtar bir halkaya kaç farklı şekilde dizilebilir?

Çözüm

$\displaystyle \frac{{(6-1)!}}{2}=\frac{{5!}}{2}=\frac{{120}}{2}=60$ farklı şekilde dizilebilir.

Not: Anahtarlıkta maskot varsa 1 eksiltme işlemi yapılmaz. Çünkü sabit bir eleman vardır. Ama 2’ye bölme işlemi yapılır. Çünkü halkaların tersi ya da düzü diye bir ayrımı yoktur.

Örnek:

6 farklı anahtar dairesel ve maskotlu bir anahtarlığa kaç farklı şekilde dizilebilir?

Çözüm

$\displaystyle \frac{{6!}}{2}=\frac{{720}}{2}=360$ farklı şekilde dizilebilir.

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)

Konu Bitti. Çözümlü Soruları ve Çıkmış Soruları Görmek için Tıkla

Sayfalar: 1 2 3