Konu ile ilgili Çözümlü Soruları veya Çıkmış Soruları Görmek için Tıkla
SAYMA YÖNTEMLERİ
1.Toplama Yöntemi
A ve B ayrık iki işlem olsun. A işi m yolla, B işi de n yolla yapılabiliyorsa A veya B işi m+n yoluyla yapılabilir.
Örnek:
Fırat’ın 3 farklı futbol topu, 2 farklı basketbol topu ve 4 farklı voleybol topu vardır. Bu toplardan birini arkadaşına vermek üzere seçecektir. Bu seçimini kaç farklı şekilde yapabilir?
Cevabı Görmek için Tıklayınız.
Topların sayısını toplamalıyız.
3+2+4=9 dur. Fırat, bu 9 toptan birini seçecektir. Dolayısıyla
Fırat, 9 farklı seçim yapabilir.
2. Çarpma Yöntemi
A ve B ayrık iki işlem olsun. A işi m yolla, B işi de n yolla yapılabiliyorsa; Bu iki işlem birlikte m.n yoluyla yapılabilir.
Örnek:
Özlem’in 3 farklı pantolonu, 5 farklı tişörtü ve 2 farklı ayakkabısı vardır. Özlem, bunlardan birer tane seçerek kaç farklı şekilde giyinebilir?
Cevabı Gör.
3.5.2=30 farklı şekilde giyinebilir.
Alıştırma 2

| | | | | |
Çözüm

Alıştırma 3

| | | | | |
Çözüm
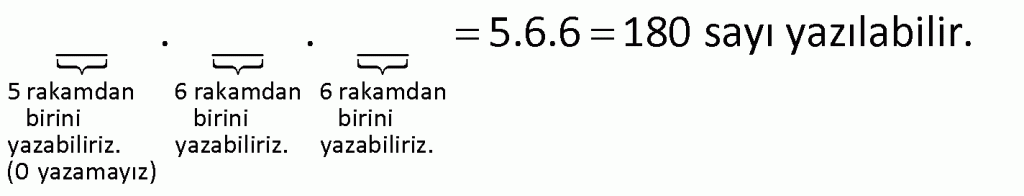
Alıştırma 4

 | | | | |
Çözüm

Alıştırma 5

| | | | | |
Çözüm

Alıştırma 6 (Posta Kutusu)

| | | | | |
Çözüm