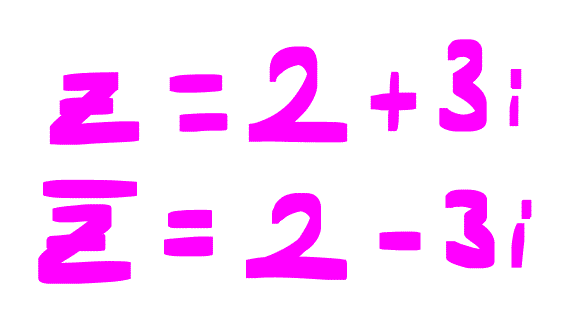
Sanal (İmajiner) Sayı Birimi
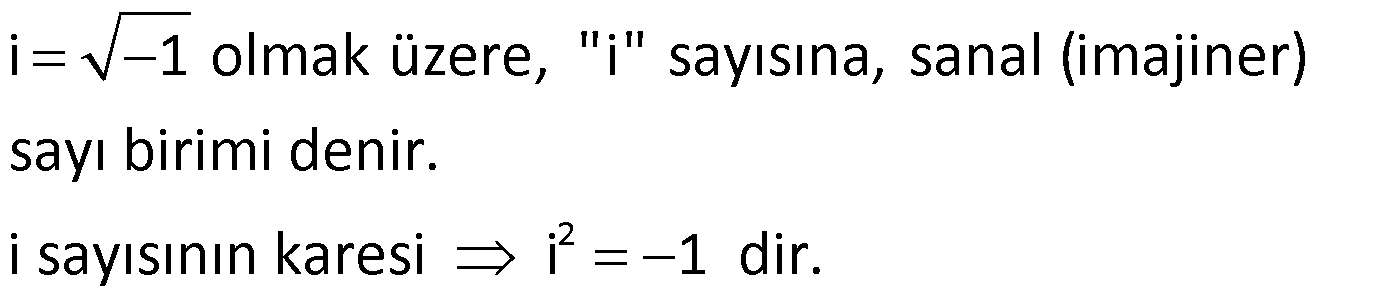
Örnek:

Çözüm:
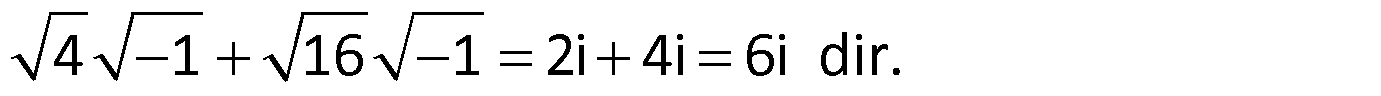
Not:

Örnek:

Çözüm:
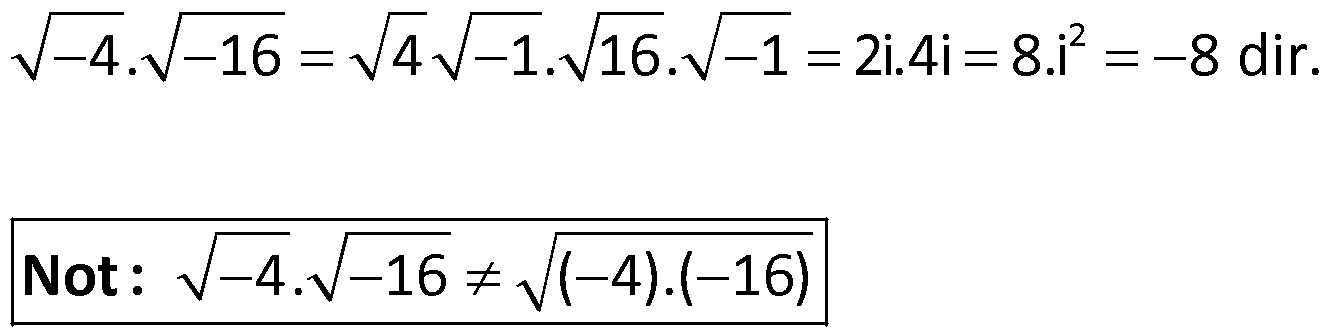
Not:
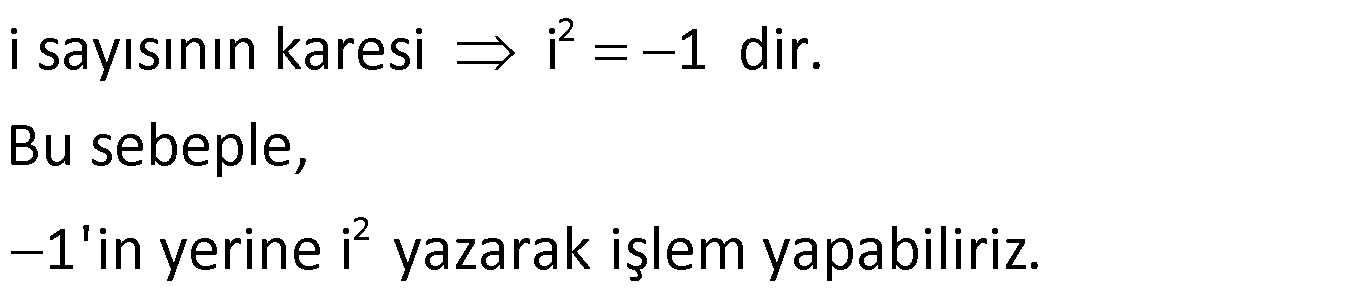
Örnek:
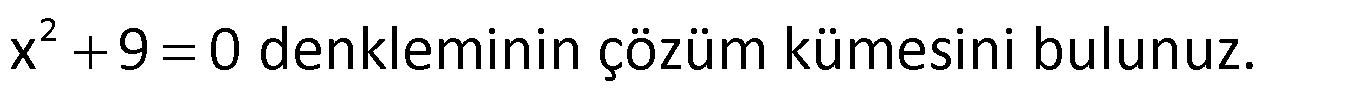
Çözüm:
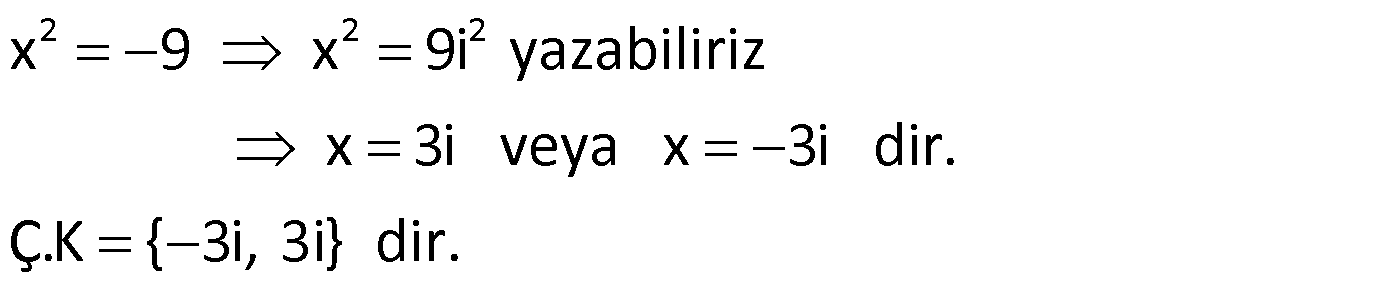
Örnek:
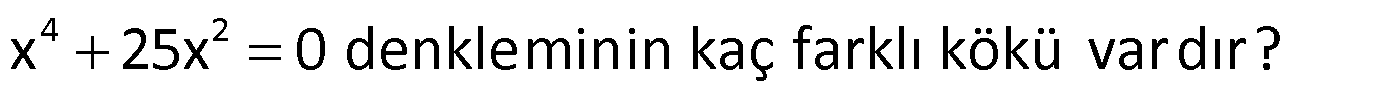
Çözüm:
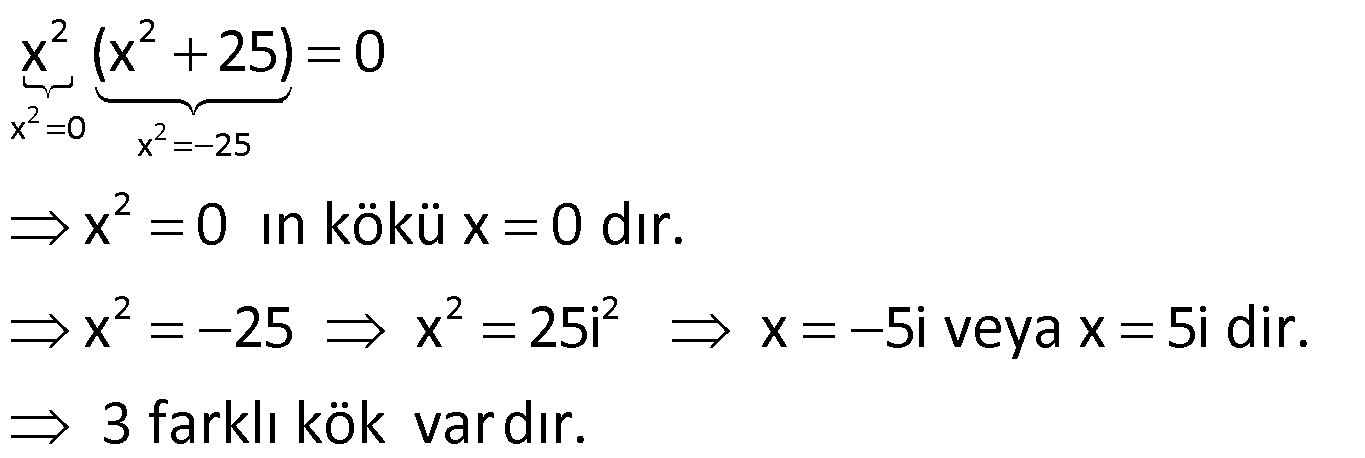
Örnek:
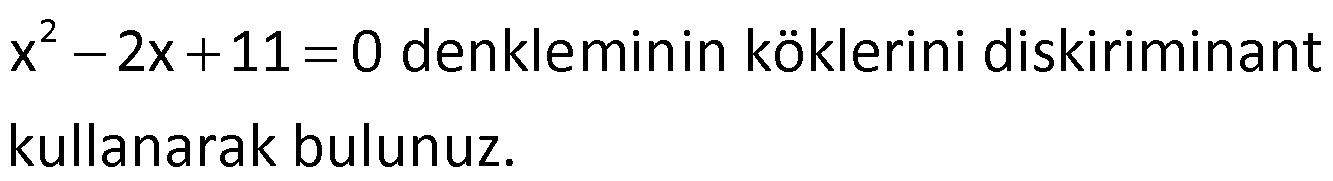
Çözüm:

i’nin Kuvvetleri
i’nin kuvvetleri her 4’te bir kendini tekrarlar. Yüksek dereceden bir kuvvet verilmişse, onun 4 ile bölümünden kalana bakmamız yeterlidir.
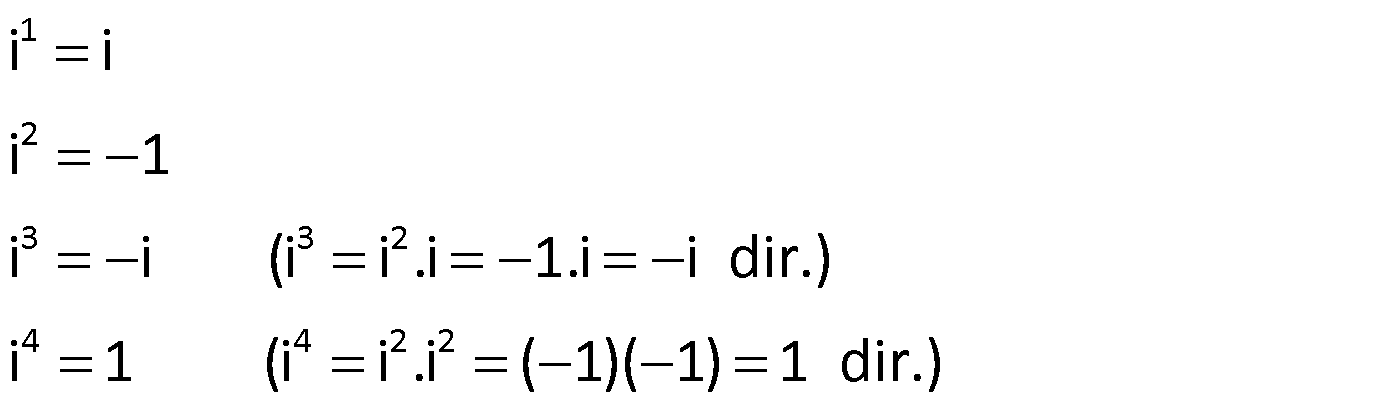
Örnek:

Çözüm:

Not: Ardışık 4 kuvvetin toplamı 0 dır.
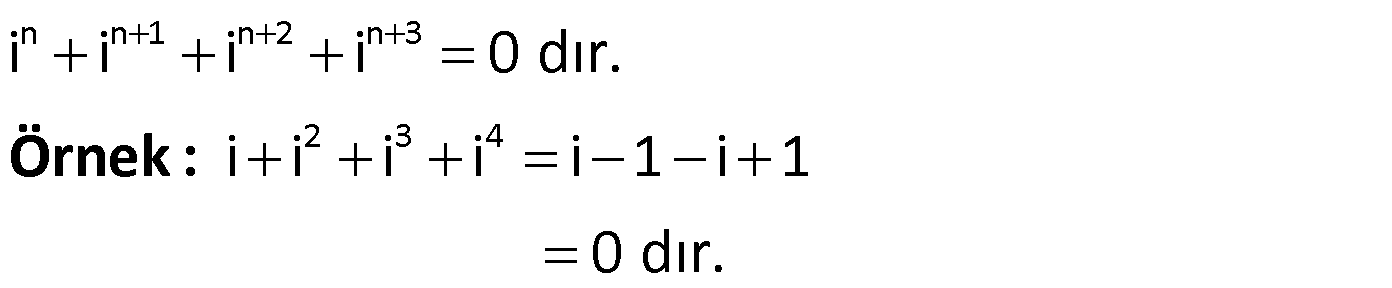
Örnek:

Çözüm:

Not: Eğer i’nin kuvveti negatif tam sayı ise, üstüne 4’ün katları eklenerek neye eşit olduğu bulunabilir.
Örnek:

Çözüm:

Karmaşık Sayılar Kümesi

Örnek:
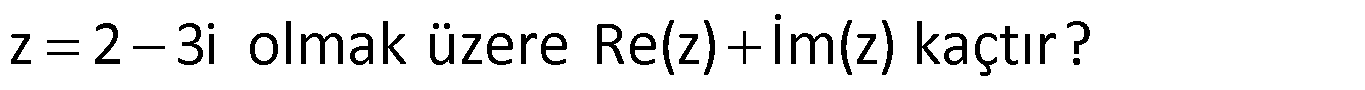
Çözüm:

Örnek:
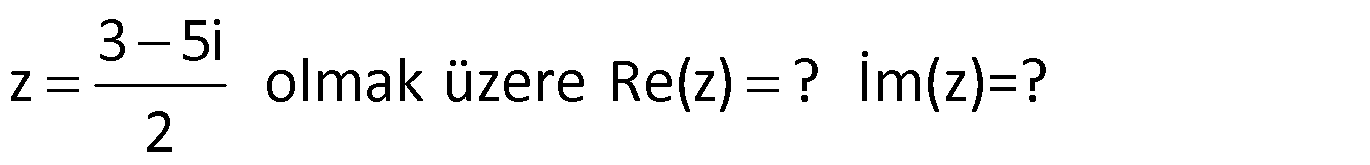
Çözüm:
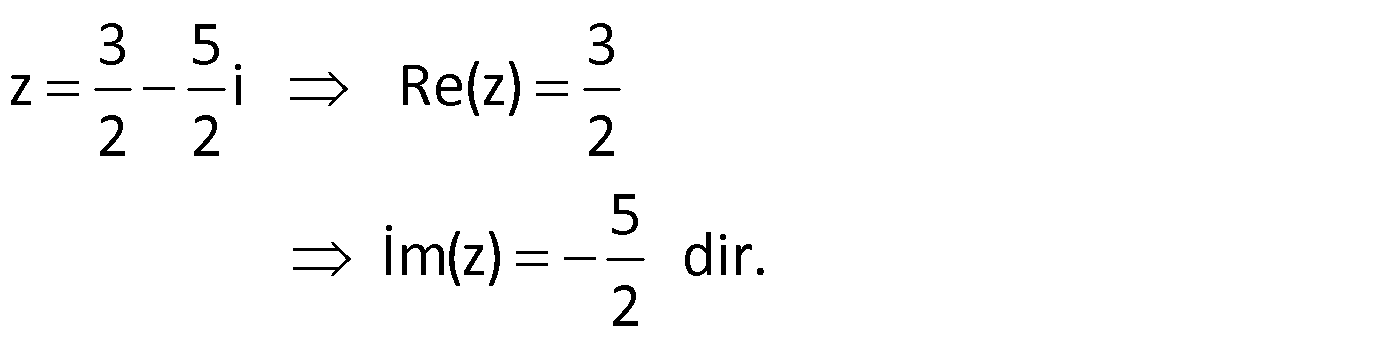
Örnek:

Çözüm:

Karmaşık Sayıların Eşitliği
İki karmaşık sayının eşit olması için reel ve imajiner kısımların ayrı ayrı eşit olması gerekir.
Örnek:
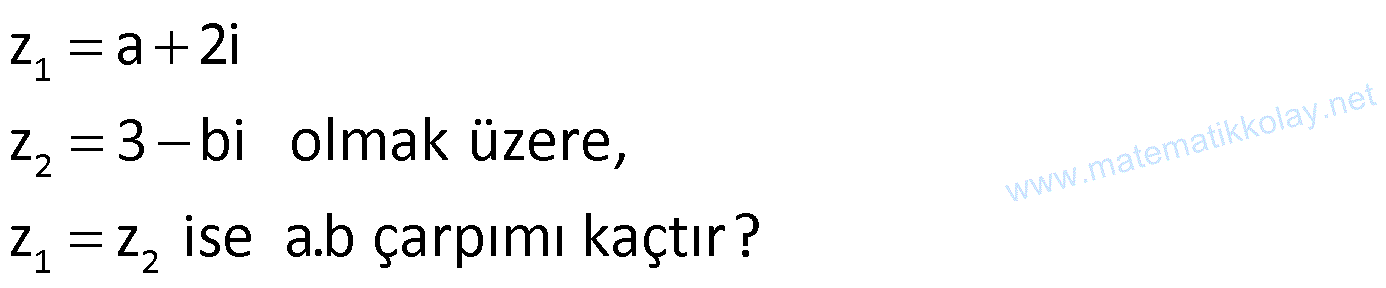
Çözüm:
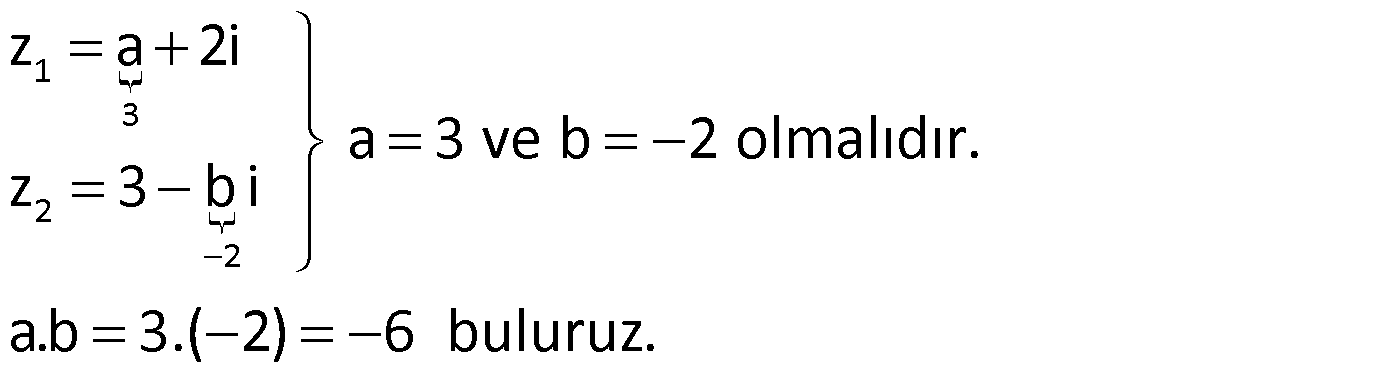
Örnek:
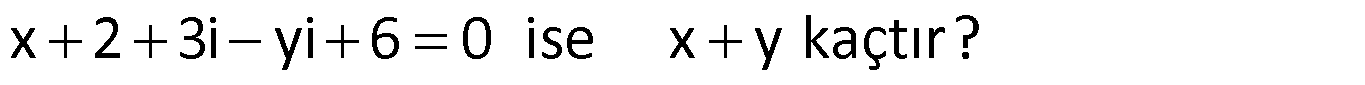
Çözüm:

Karmaşık Sayılarda Toplama Çıkarma
Reel kısımlar kendi arasında, imajiner kısımlar da kendi arasında toplanır ve çıkarılır.
Örnek:
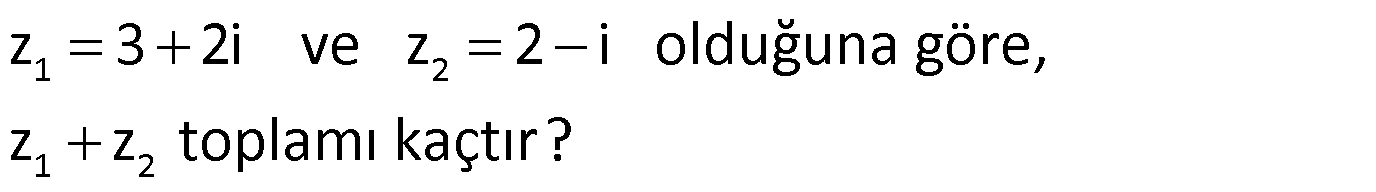
Çözüm:
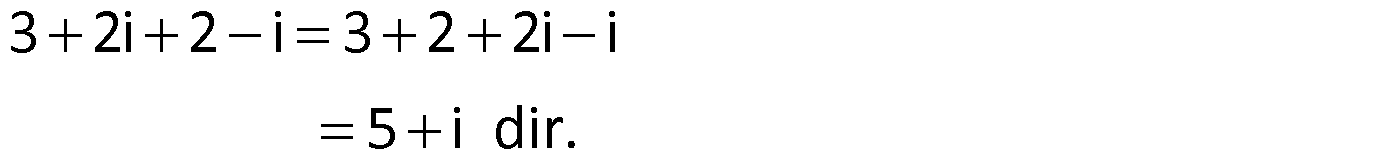
Örnek:
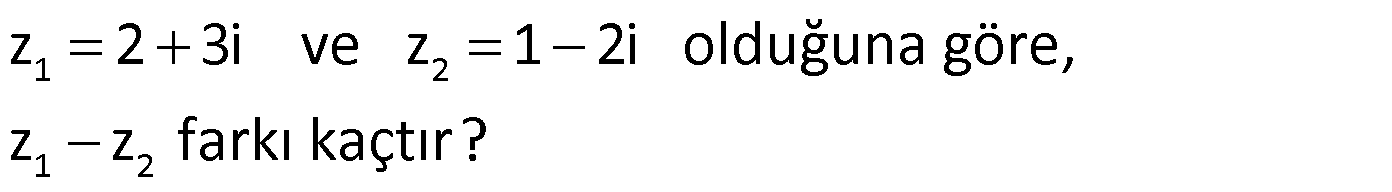
Çözüm:
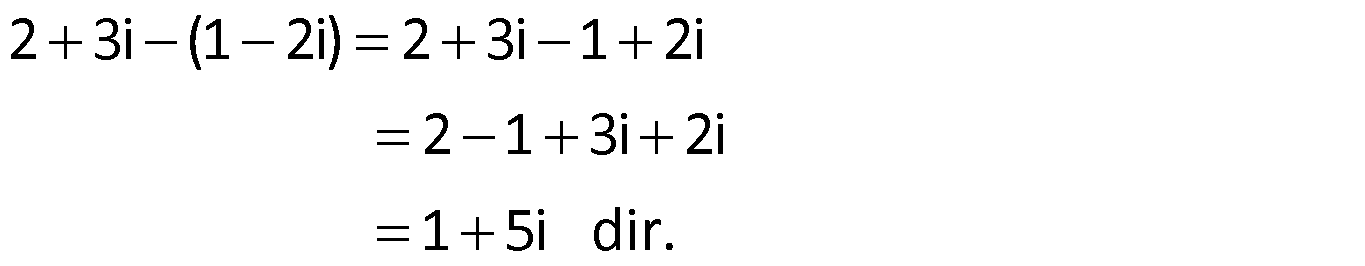
Karmaşık Sayılarda Çarpma
Dağılma özelliğinden yararlanarak çarpma yapabiliriz.
Örnek:
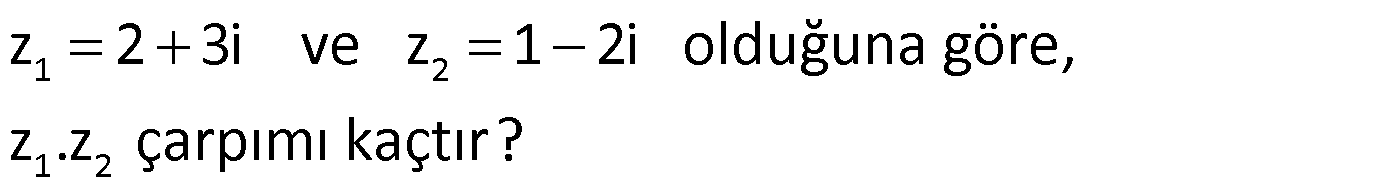
Çözüm:
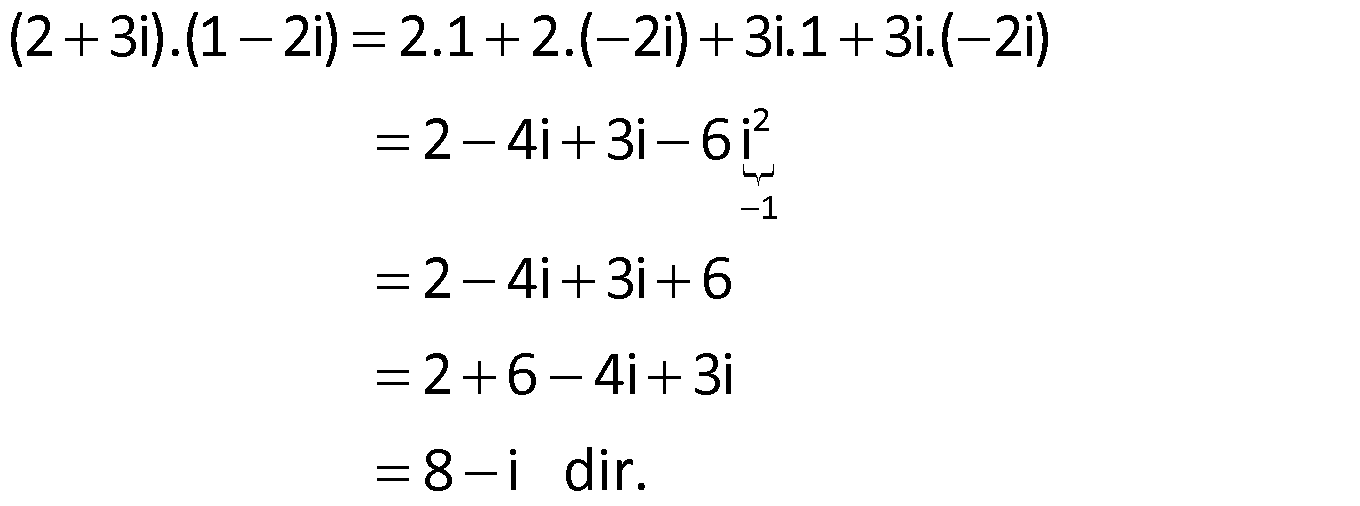
Örnek:
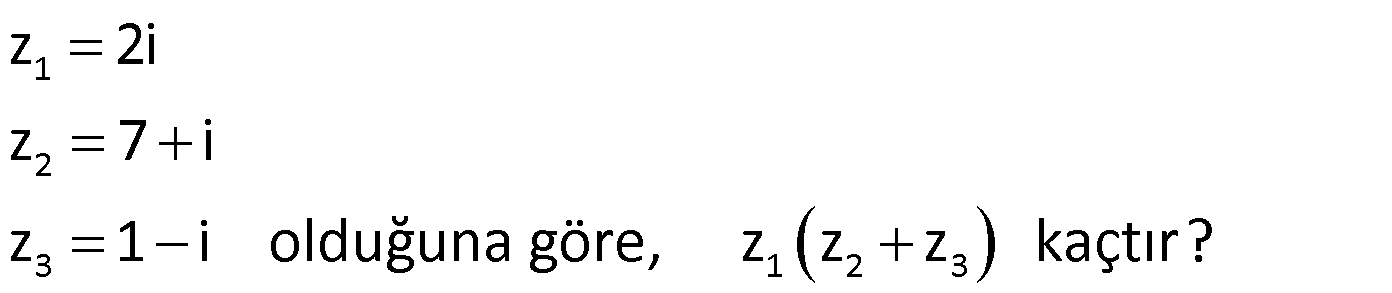
Çözüm:
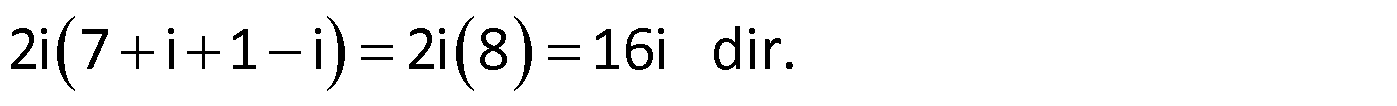
Not:

Örnek:

Çözüm:
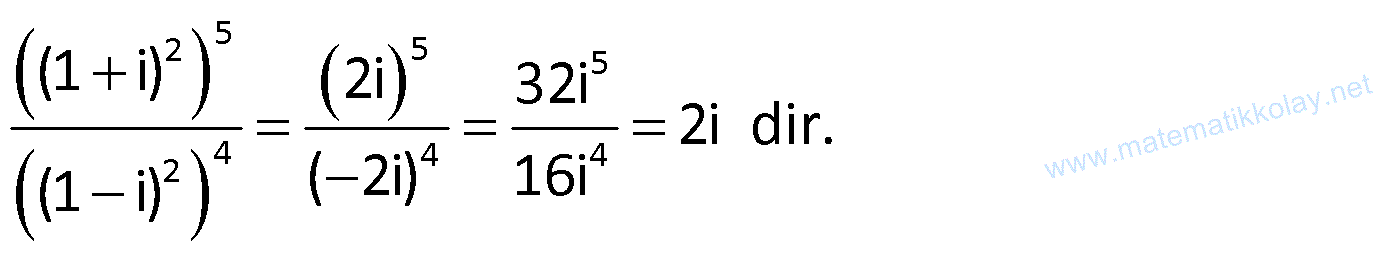
Örnek:

Çözüm:
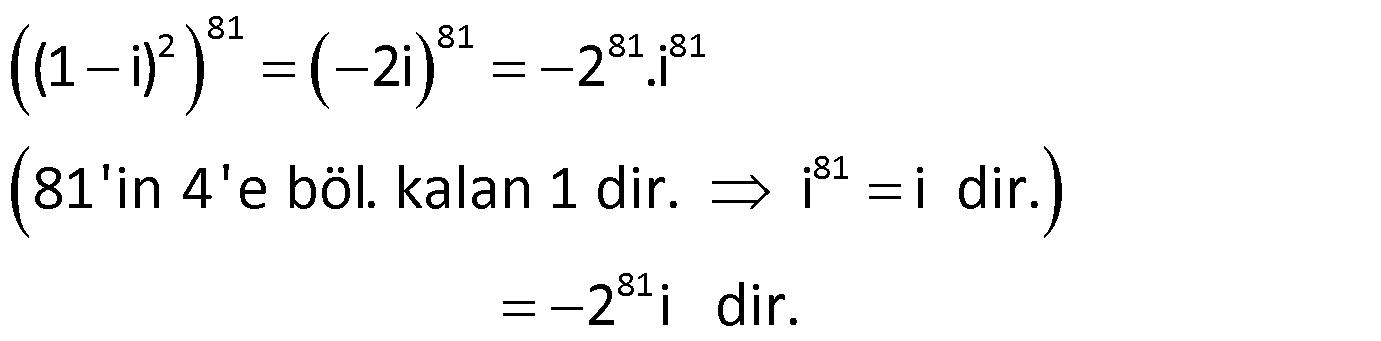
Karmaşık Sayının Eşleniği

Örnek:

Örnek:
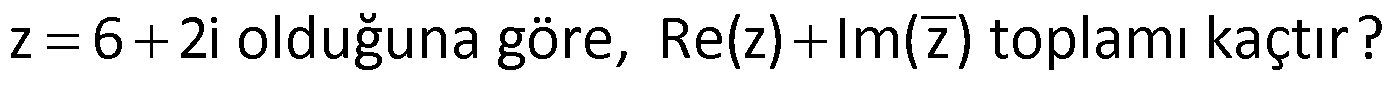
Çözüm:
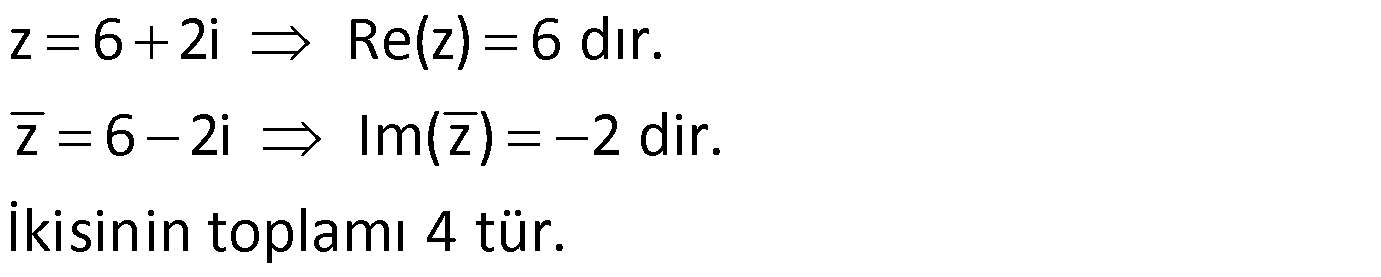
Örnek:
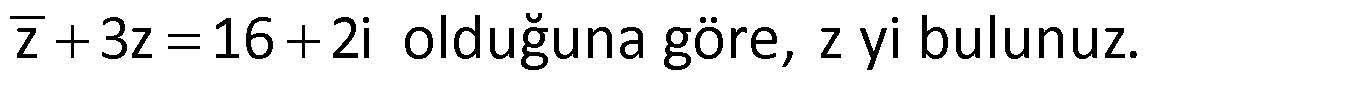
Çözüm:

Not: Karmaşık sayının eşleniğinin eşleniği kendisine eşittir.

Örnek:

Çözüm:

Not: Karmaşık sayı ile eşleniğinin çarpımı, reel ve imajiner kısımlarının kareleri toplamına eşittir.
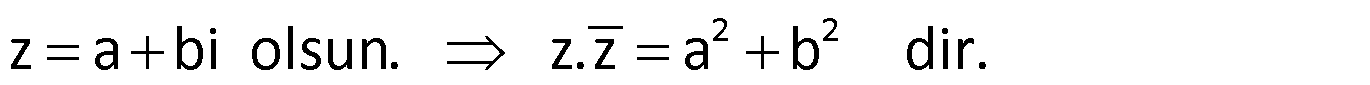
Örnek:

Çözüm:
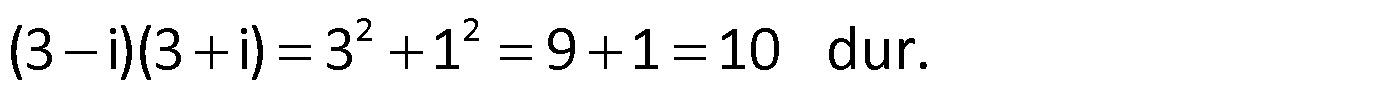
Not: Eğer paydada karmaşık sayı varsa, paydayı reel yapmak için eşlenikle çarparız.
Örnek:

Çözüm:
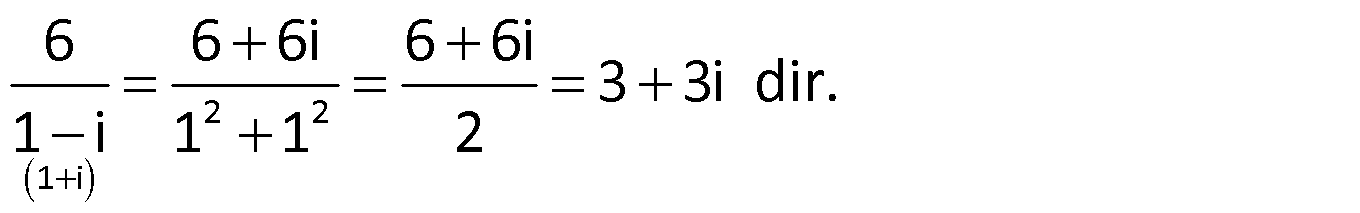
Not: (Kökler Karmaşık Sayı ise)

Örnek:

Çözüm:
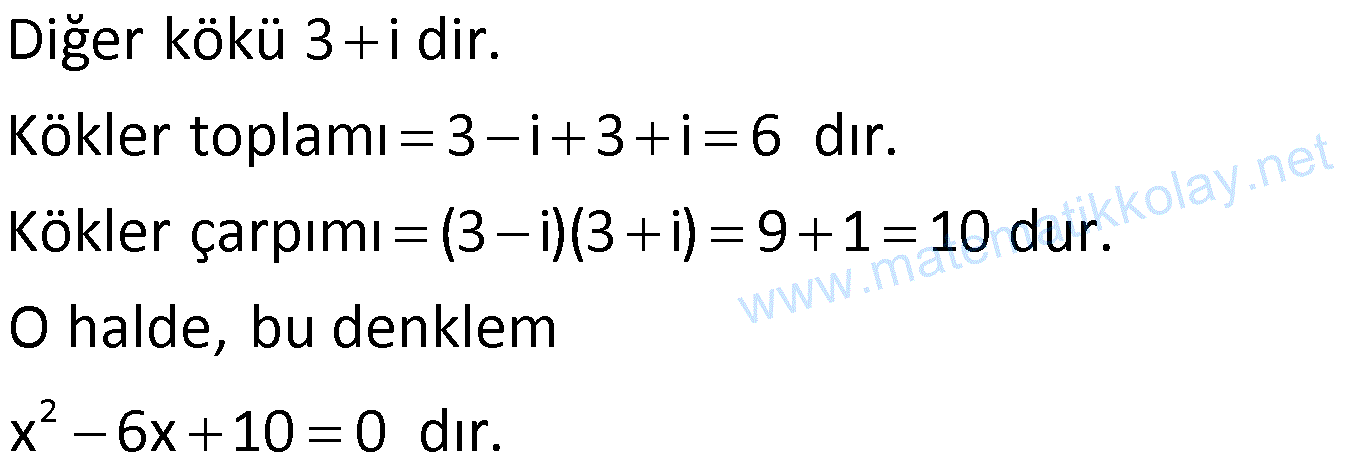
Çözümlü Sorular veya Çıkmış Sorular için Tıkla
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
KARMAŞIK SAYILAR KONU ANLATIMI www.matematikkolay.net Sanal (İmajiner) Sayı Birimi 2 i 1 olmak üzere, “i” sayısına, sanal (imajiner) sayı birimi denir. i sayısının karesi i 1 dir. Örnek: 4 16 ? Çözüm: 4 1 16 1 2i4i 6i dir. Not: Örnek: 4. 16 ? Çözüm: 2 4. 16 4 1. 16. 1 2i.4i 8.i 8 dir. 4. 16 ( 4).( 16) Not : Not: 2 2 i sayısının karesi i 1 dir. Bu sebeple, 1’in yerine i yazarak işlem yapabiliriz. Örnek: 2 x 9 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2 2 x 9 x 9i yazabiliriz x 3i veya x 3i dir. Ç.K { 3i, 3i} dir. Örnek: 4 2 x 25x 0 denkleminin kaç farklı kökü vardır? Çözüm: Örnek: 2 x 2x 11 0 denkleminin köklerini diskiriminant kullanarak bulunuz. Çözüm: 2 2 1 b 4ac ( 2) 4.1.11 4 44 40 tır. 0 olduğu için reel kökü yoktur. Ancak i sayısını kullanarak karmaşık köklerini bulabiliriz. b 2 40 2 40 1 2 2 10.i x 2a 2 2 2 2 1 10 i dir. Diğer kökü de x 1 10 i dir. i’nin Kuvvetleri 1 2 3 3 2 4 4 2 2 i i i 1 i i (i i .i 1.i i dir.) i 1 (i i .i ( 1)( 1) 1 dir.) i’nin kuvvetleri her 4’te bir kendini tekrarlar. Yüksek dereceden bir kuvvet verilmişse, onun 4 ile bölümünden kalana bakmamız yeterlidir. Örnek: 102 103 i i ? Çözüm: www.matematikkolay.net Not: Ardışık 4 kuvvetin toplamı 0 dır. Örnek: 13 14 15 82 i i i …i ? Çözüm: 13 14 15 16 80 81 82 81 82 0 82 13 Terim Sayısı= 1 70 dir. 1 70’in 4 ile bölümünden kalan 2 dir. Son 2 terim hariç diğerlerinin toplamı 0 olacaktır. i i i i … i i i i i 1 2 i i i 1 1 i dir. Not: Eğer i’nin kuvveti negatif tam sayı ise, üstüne 4’ün katları eklenerek neye eşit olduğu bulunabilir. Örnek: 83 83 i i ? Çözüm: 4’ün katı 83 1 83 3 83’e 84 ekleyelim. i i i dir. 83’ün 4 ile bölümünden kalan 3 tür. i i i dir. İkisinin toplamı i ( i) 0 dır. Karmaşık Sayılar Kümesi Örnek: z 23i olmak üzere Re(z)İm(z) kaçtır? Çözüm: reel imajiner z 2 3 i Re(z) İm(z) 2 3 1 dir. Örnek: 3 5i z olmak üzere Re(z) ? İm(z)=? 2 Çözüm: 3 5 3 z i Re(z) 2 2 2 5 İm(z) dir. 2 Örnek: 9 9 sayısının reel kısmı ile imajiner kısmının toplamı kaçtır? Çözüm: 9 9. 1 3 3i dir Reel kısmı 3 Toplamları 6 dır. İmajiner kısmı 3 Karmaşık Sayıların Eşitliği İki karmaşık sayının eşit olması için reel ve imajiner kısımların ayrı ayrı eşit olması gerekir. Örnek: Çözüm: 1 3 2 2 z a 2i a 3 ve b 2 olmalıdır. z 3 b i a.b 3.( 2) 6 buluruz. www.matematikkolay.net Örnek: x 23iyi6 0 ise x y kaçtır? Çözüm: Burası 0 olmalı Burası da 0 olmalı Reel kısım ile sanal kısmı ayıralım. x 2 6 (3 y) i 0 x 8 dir. y 3 tir. x y 8 3 5 buluruz. Karmaşık Sayılarda Toplama Çıkarma Reel kısımlar kendi arasında, imajiner kısımlar da kendi arasında toplanır ve çıkarılır. Örnek: 1 2 1 2 z 3 2i ve z 2 i olduğuna göre, z z toplamı kaçtır? Çözüm: 3 2i 2 i 3 2 2i i 5 i dir. Örnek: 1 2 1 2 z 2 3i ve z 1 2i olduğuna göre, z z farkı kaçtır? Çözüm: 2 3i (1 2i) 2 3i 1 2i 2 1 3i 2i 1 5i dir. Karmaşık Sayılarda Çarpma Dağılma özelliğinden yararlanarak çarpma yapabiliriz. Örnek: 1 2 1 2 z 2 3i ve z 1 2i olduğuna göre, z .z çarpımı kaçtır? Çözüm: 2 1 (2 3i).(1 2i) 2.1 2.( 2i) 3i.1 3i.( 2i) 2 4i 3i 6i 2 4i 3i 6 2 6 4i 3i 8 i dir. Örnek: 1 2 3 1 2 3 z 2i z 7 i z 1 i olduğuna göre, z z z kaçtır? Çözüm: 2i7i1i 2i8 16i dir. Not: Örnek: 10 8 1 i ? (1 i) Çözüm: 2 5 5 5 2 4 4 4 (1 i) 2i 32i 2i dir. (1 i) ( 2i) 16i Örnek: 162 (1i) ? Çözüm: 2 81 81 81 81 81 81 (1 i) 2i 2 .i 81’in 4’e böl. kalan 1 dir. i i dir. 2 i dir. www.matematikkolay.net Karmaşık Sayının Eşleniği a ve b birer gerçek sayı olmak üzere, z a ib nin eşleniği z a ib dir. Yani, imajiner kısım işaret değiştirir. Örnek: Örnek: z 6 2i olduğuna göre, Re(z) Im( z) toplamı kaçtır? Çözüm: z 6 2i Re(z) 6 dır. z 6 2i Im(z) 2 dir. İkisinin toplamı 4 tür. Örnek: z 3z 162i olduğuna göre, z yi bulunuz. Çözüm: Not: Karmaşık sayının eşleniğinin eşleniği kendisine eşittir. (z) z dir. Örnek: (z) z z 92i olduğuna göre z kaçtır? Çözüm: 3 2 z a bi olsun. (z) z z 9 2i denkleminde yerine yazarsak, a bi a bi a bi 9 2i 3a b i 9 2i z 3 2i dir. Not: Karmaşık sayı ile eşleniğinin çarpımı, reel ve imajiner kısımlarının kareleri toplamına eşittir. 2 2 z abi olsun. z.z a b dir. Örnek: (3i)(3i) ? Çözüm: 2 2 (3i)(3i) 3 1 9110 dur. Not: Eğer paydada karmaşık sayı varsa, paydayı reel yapmak için eşlenikle çarparız. Örnek: 6 ? 1 i Çözüm: 2 2 1 i 6 6 6i 6 6i 3 3i dir. 1 i 1 1 2 Not: (Kökler Karmaşık Sayı ise) Gerçek katsayılı ikinci dereceden bir denklemin köklerinden biri a bi ise diğer kökü a bi dir. Yani eşleniğidir. Örnek: Köklerinden biri 3 i olan rasyonel katsayılı ikinci dereceden denklemi bulunuz. Çözüm:


elinize sağlık
Teşekkürler.