Soru Sor sayfası kullanılarak Geometrik Kavramlar ve Açı konusu altında Paralel iki doğru arasındaki açıların toplamı, Kalem Ucu, U kuralı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU

3.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
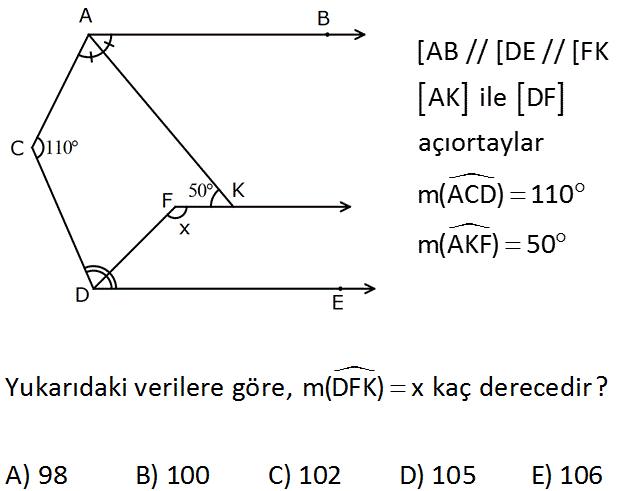
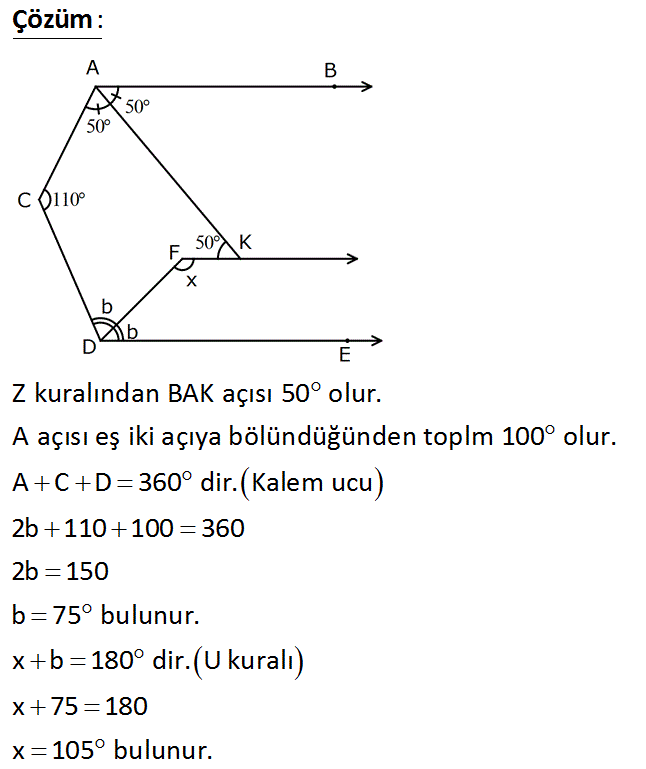
www.matematikkolay.net [AB // [DE // [FK AK ile DF açıortaylar m(ACD) 110 m(AKF) 50 Yukarıdaki verilere göre, m(DFK) x kaç derecedir? A) 98 B) 100 C) 102 D) 104 E) 106 : Çözüm Z kuralından BAK açısı 50 olur. A açısı eş iki açıya bölündüğünden toplm 100 olur. A C D 360 dir. Kalem ucu 2b 110 100 360 2b 150 b 75 bulunur. x b 180 dir. U kuralı x 75 180 x 105 bulunur. www.matematikkolay.net 30
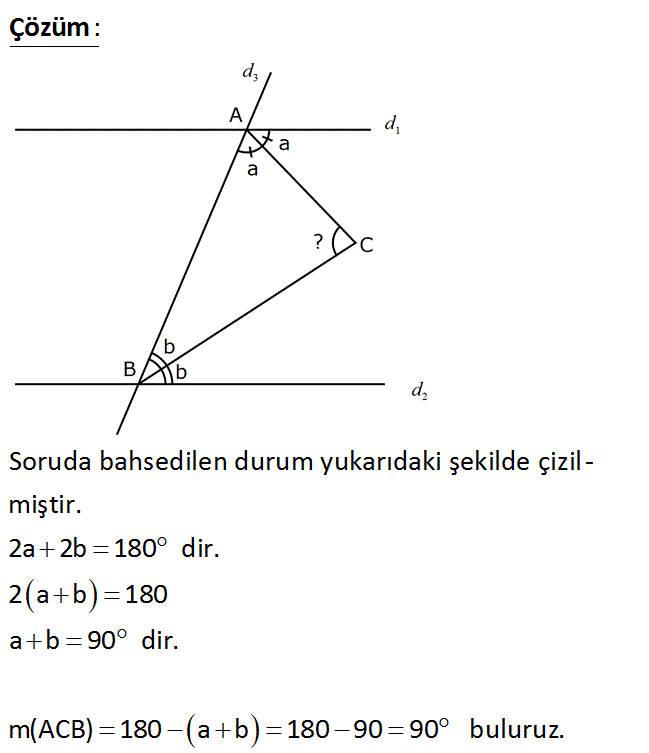
1 2 3 Düzlemde birbirine paralel olan d ve d doğruları ile bu doğruları A ve B noktalarında kesen bir d doğ – rusu veriliyor. A ve B noktalarındaki açılara çizilen açıortay doğru – larından ikisi C noktasında kesiştiğine göre, m(ACB) kaç derecedir? A) 75 B) 80 C) 85 D) 90 E) 95 Çözüm: www.matematikkolay.net Soruda bahsedilen durum yukarıdaki şekilde çizil – miştir. 2a 2b 180 dir. 2 a b 180 a b 90 dir. m(ACB) 180 a b 180 90 90 buluruz.
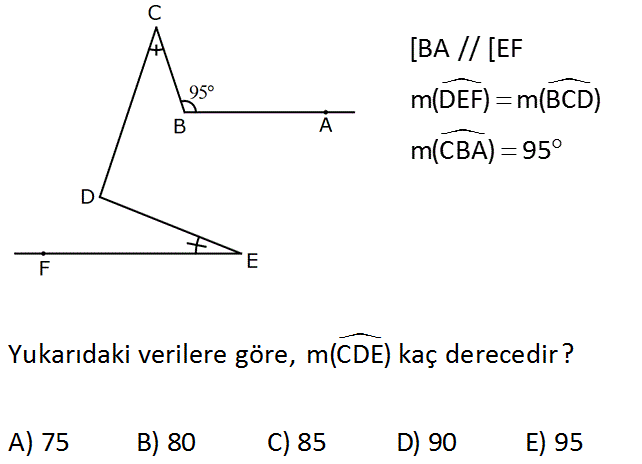
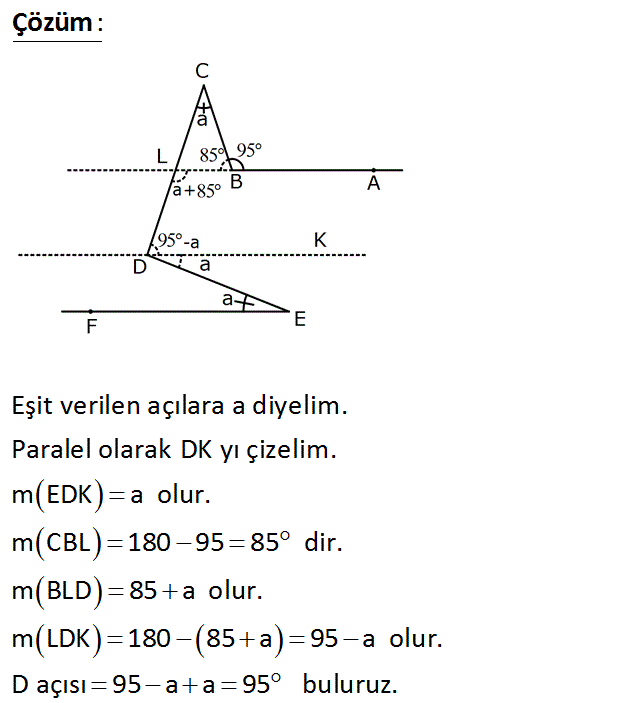
[BA // [EF m(DEF) m(BCD) m(CBA) 95 Yukarıdaki verilere göre, m(CDE) kaç derecedir? A) 75 B) 80 C) 85 D) 90 E) 95 Çözüm: www.matematikkolay.net Eşit verilen açılara a diyelim. Paralel olarak DK yı çizelim. m EDK a olur. m CBL 180 95 85 dir. m BLD 85 a olur. m LDK 180 85 a 95 a olur. D açısı 95 a a 95 buluruz. 36


Çok iyi bir site olmuş.
ADAMSINIZZ👌👊👏
Merhabalar, ilk soruda cevap şıklarda yok, bunu lütfen düzeltebilir misiniz?
Sitenizi çok seviyorum…
Uyarınız için teşekkürler. Yazım hatası düzeltildi.