Soru Sor sayfası kullanılarak Fonksiyonlar konusu altında Fonksiyonda değer bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
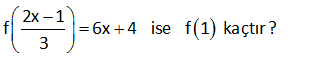

2.SORU
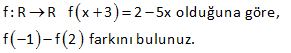

3.SORU


4.SORU


5.SORU


6.SORU
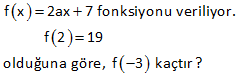
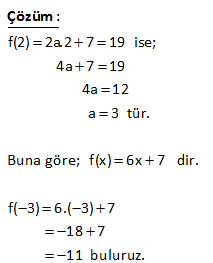
7.SORU
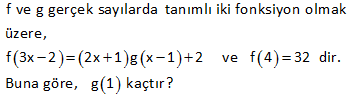

8.SORU

9.SORU
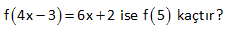

10.SORU
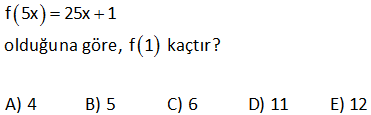
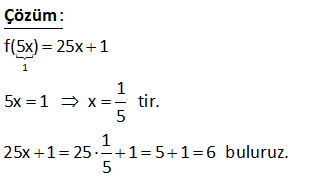
11.SORU
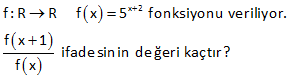
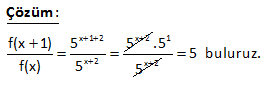
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
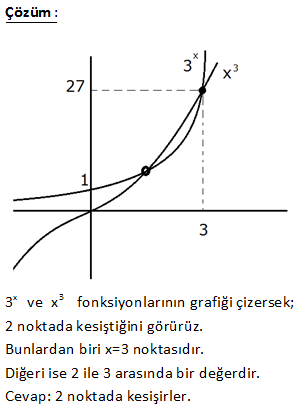
2x 1 f 6x 4 ise f 1 kaçtır? 3 1 2 Fonksiyonun içini 1’e eşitleyelim. Sonra bulduğumuz x değerini karşı tarafta kullanalım. 2x 1 f 6x 4 3 2x 1 1 2x 1 3 2x 4 x 2 dir. 3 Buna göre; 6x 4 6.2 4 12 4 16 bulur : uz Çözüm . f(1) 16 dır. 50 f :R R f x 3 2 5x olduğuna göre, f 1 f 2 farkını bulunuz. 1 4 2 1 f(x 3) 2 5x x 3 1 x 4 yazılacak f( 1) 2 5 x 2 5.( 4) 2 20 22 buluruz. f(x 3) 2 5x x 3 2 x 1 yazılacak f( 1) 2 5 x 2 5.( 1) 2 5 7 buluruz. f( 1) f(2) 22 7 15 buluruz : . Çözüm 72 www.matematikkolay.net f : R R, f x 2x 1 olarak tanımlanan f fonksi – yonuna göre, f a 1 f a 4 f 5 f a eşitliğini sağlayan a değeri kaçtır? f(a 1) f(a) 4 f(5) f(a) 2(a 1) 1 (2a 1) 4 2.5 1 2a 1 2a 2 1 2a 1 4 10 1 2a 1 2 12 2a 14 2a a 7 buluruz : . Çözüm 73 2 f : R R fonksiyonu x 1 x 1 f x x 1 1 x 3 4 x x 3 f 2 f 1 f 1 f 5 toplamının değeri kaçtır ? A) 4 B) 5 C) 6 D) 7 E) 8 www.matematikkolay.net 2 2 x hangi aralıktaysa o fonkisyonu uygulamalıyız. x 2 için f(x) x 1 f(2) 2 1 5 tir. x 1 için f(x) x 1 f(1) 1 1 2 dir. x 1 için f(x) x 1 f( 1) 1 1 0 dır. x 5 için : Çözüm f(x) 4 x f(5) 4 5 1 dir. Buna göre; f(2) f(1) f( 1) f(5) 5 2 0 1 6 buluruz. 79 x 1 f x 2 3 fonksiyonu veriliyor. f a 35 olduğuna göre, a kaçtır ? www.matematikkolay.net a 1 a 1 a 1 5 f(a) 2 3 35 ise; 2 32 2 2 Üsler eşit olmalıdır. a 1 5 a 6 b : uluruz. Çözüm 92 f x 2ax 7 fonksiyonu veriliyor. f 2 19 olduğuna göre, f 3 kaçtır ? f(2) 2a.2 7 19 ise; 4a 7 19 4a 12 a 3 tür. Buna göre; f(x) 6x 7 dir. f( 3) 6.( 3) 7 18 7 11 buluruz. : Çözüm 94 f ve g gerçek sayılarda tanımlı iki fonksiyon olmak üzere, f 3x 2 2x 1 g x 1 2 ve f 4 32 dir. Buna göre, g 1 kaçtır ? 2 2 2 f(3x 2) (2x 1).g(x 1) 2 x 2 yazarsak f(4)’ü kullanabiliriz. f(3x 2) (2x 1).g(x 1) 2 f(4) 5.g(1) 2 32 5.g(1) 2 30 5.g(1) g(1) 6 bulur : uz. Çözüm 98 www.matematikkolay.net 3 x f x x g x 3 fonksiyonları kaç farklı noktada kesişir? A) 1 B) 2 C) 3 D) 4 E) 5 : Çözüm x 3 3 ve x fonksiyonlarının grafiği çizersek; 2 noktada kesiştiğini görürüz. Bunlardan biri x=3 noktasıdır. Diğeri ise 2 ile 3 arasında bir değerdir. Cevap: 2 noktada kesişirler. 104 f 4x 3 6x 2 ise f 5 kaçtır? 2 : Fonksiyonun içini 5 yapan x deeğerini bulalım. 4x 3 5 4x 8 x 2 dir. Şimdi x yerine 2 yazalım. f(5) 6.x 2 6.2 2 12 2 14 buluruz. Çözüm 118 f 5x 25x 1 olduğuna göre, f 1 kaçtır? A) 4 B) 5 C) 6 D) 11 E) 12 1 f(5x) 25x 1 1 5x 1 x tir. 5 1 25x 1 25 1 5 1 6 buluru : z. 5 Çözüm 130 x 2 f :R R f x 5 fonksiyonu veriliyor. f x 1 ifadesinin değeri kaçtır? f x x 1 2 x 2 x 2 : f(x 1) 5 5 f(x) 5 Çözüm 1 x 2 .5 5 5 buluruz. 71


2. sorunun sadece yarısı yapılmış
Uyarınız için teşekkürler. Tam hali eklendi.