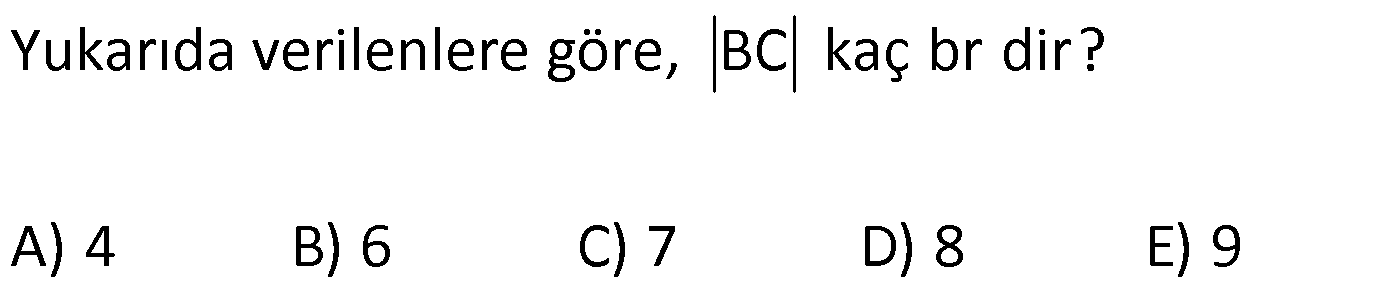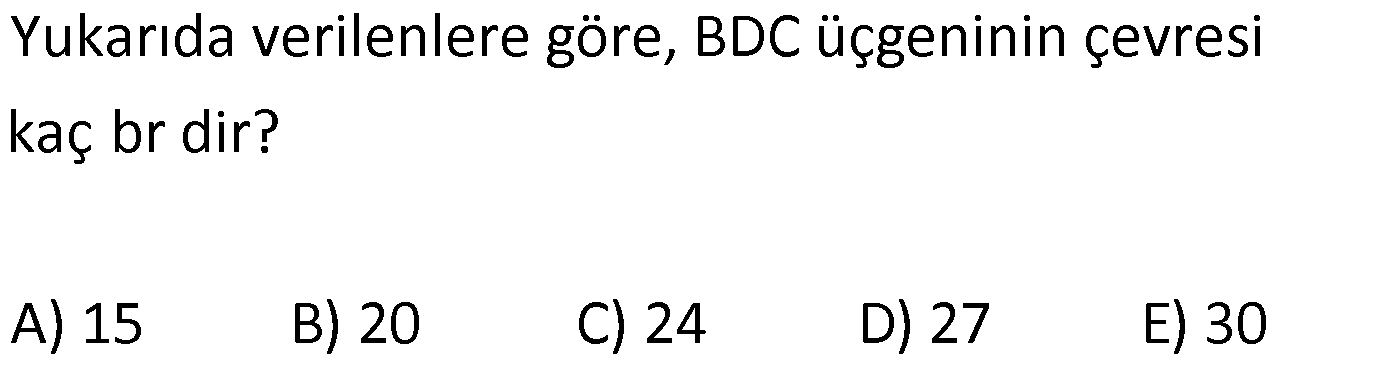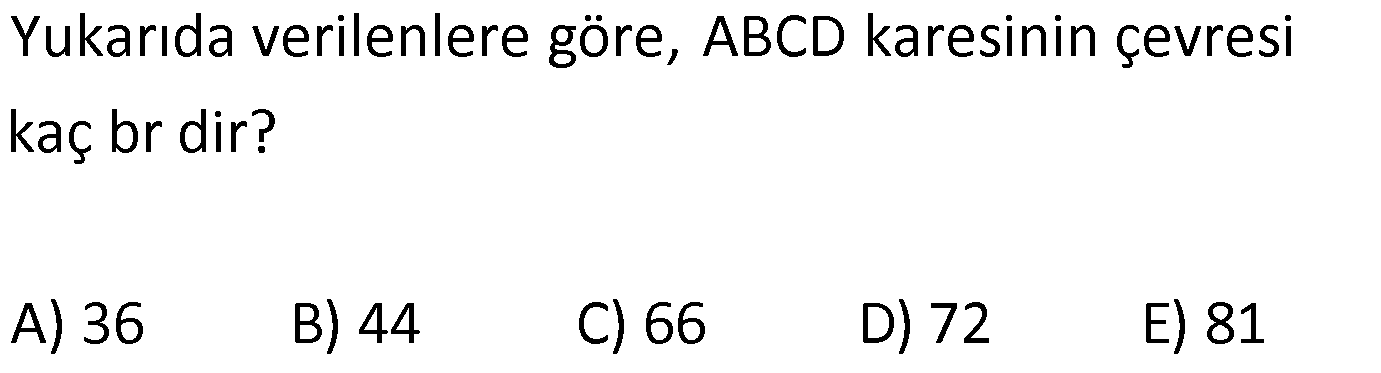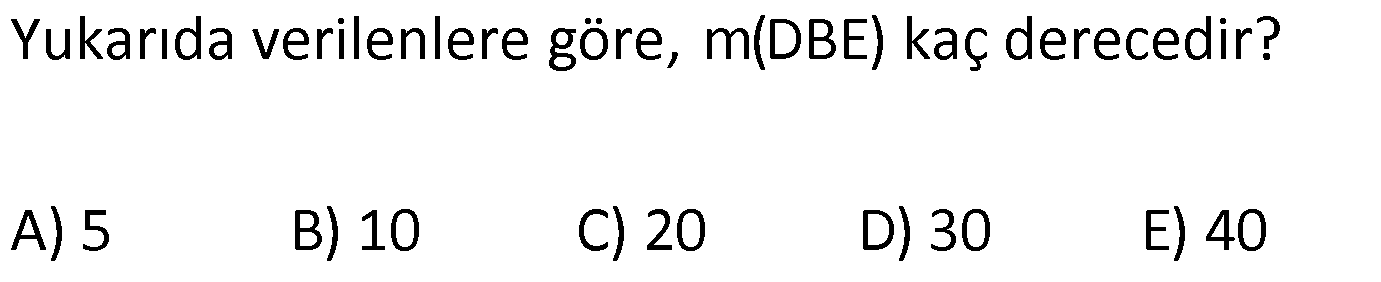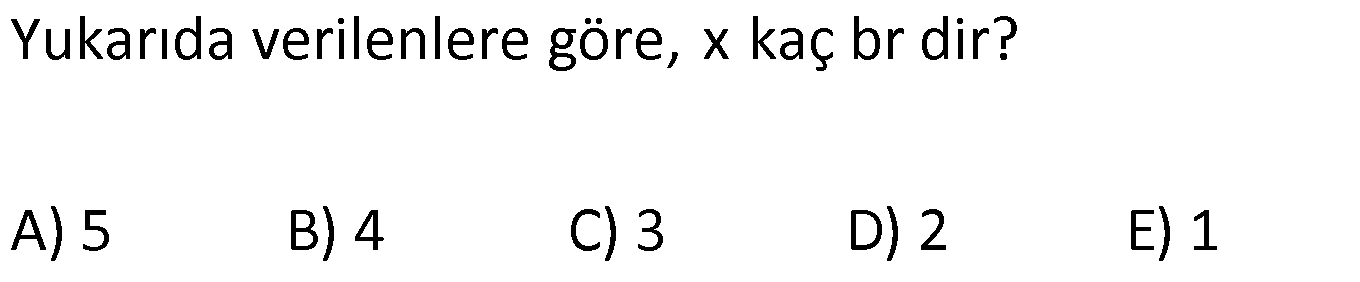Bu bölümde Üçgenlerde Eşlik ile ilgili 7 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
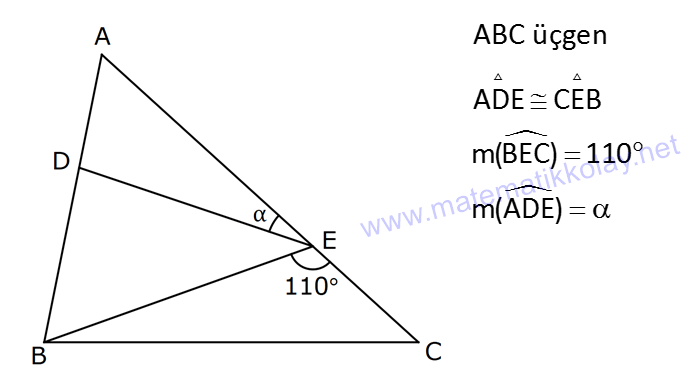
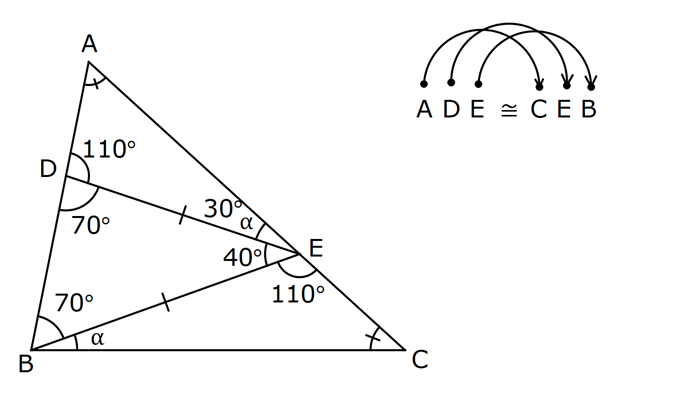
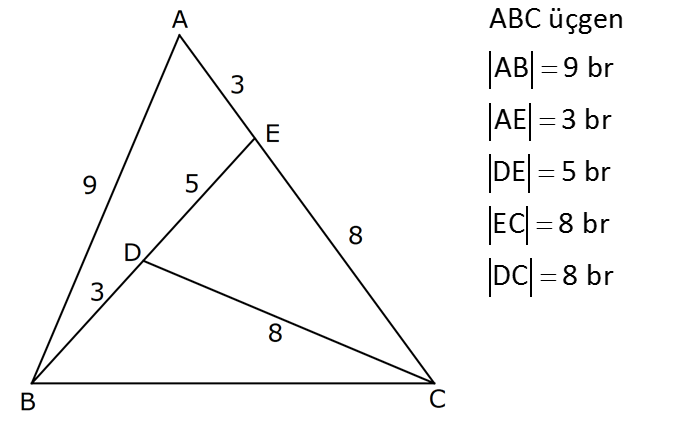
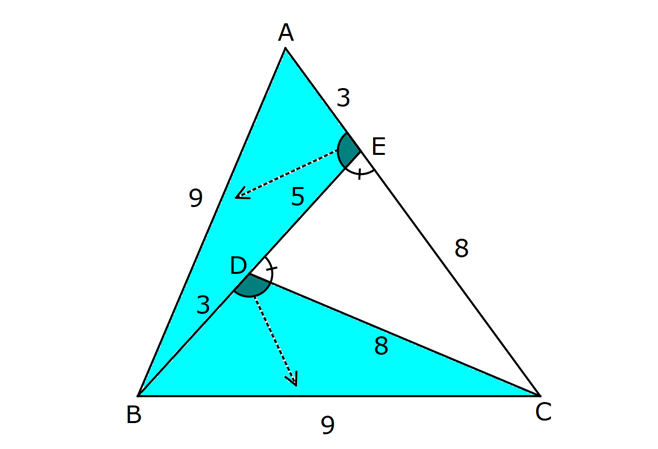
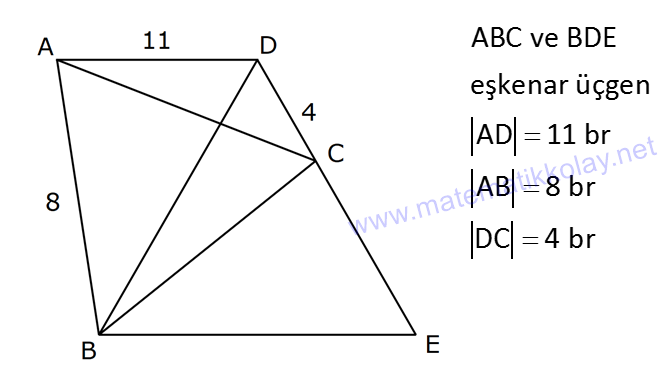
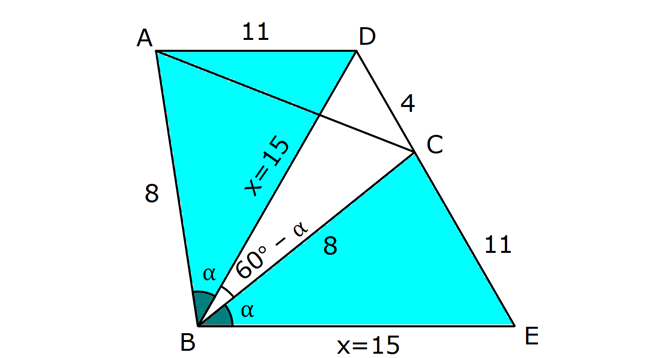
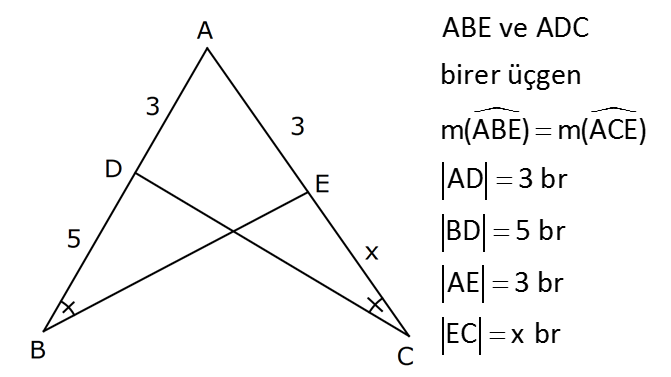
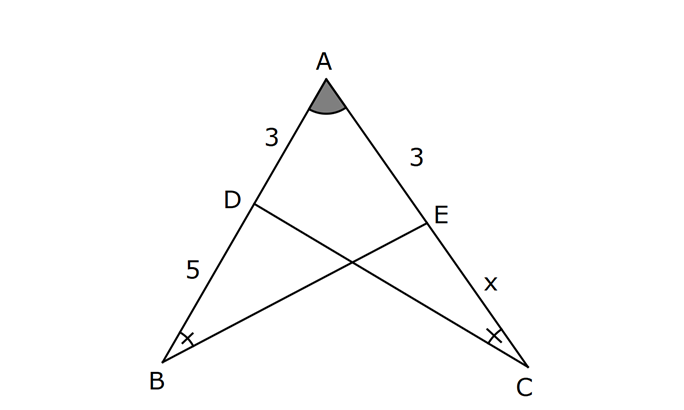
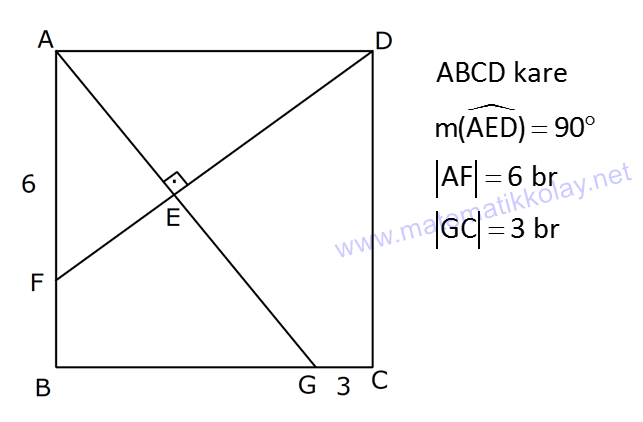
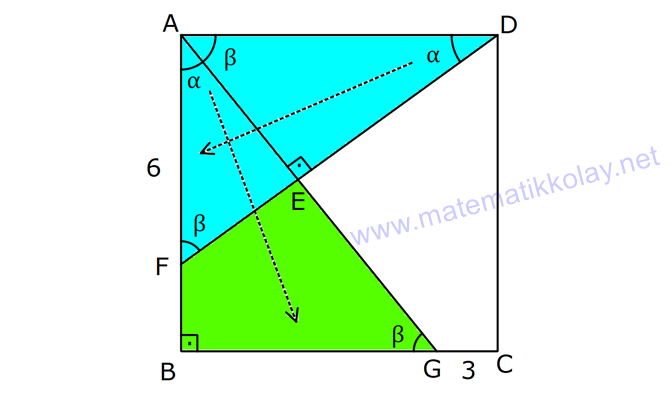
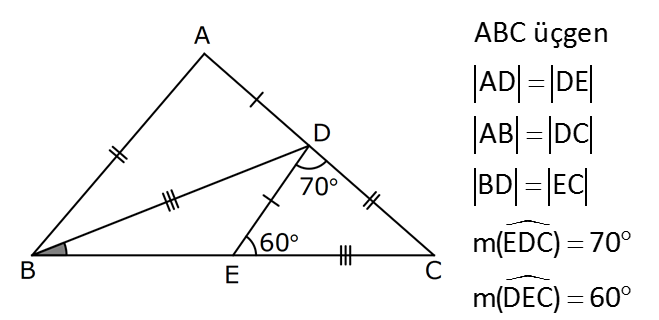
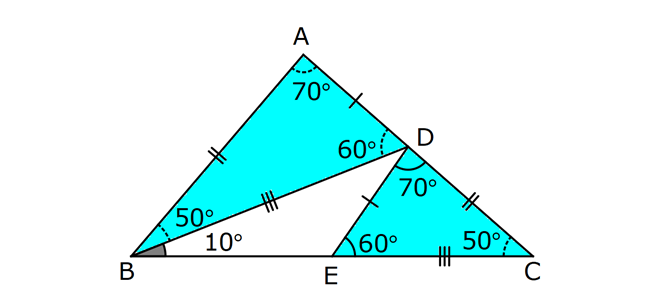
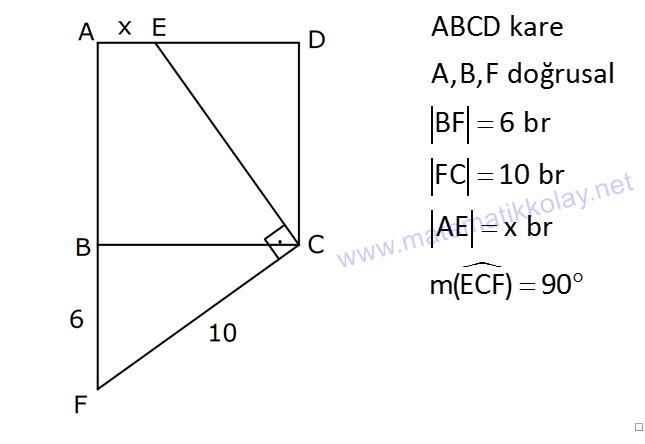
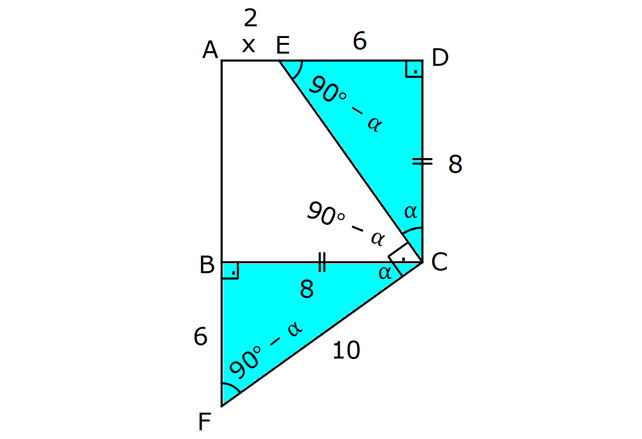
ÜÇGENLERDE EŞLİK www.matematikkolay.net 1) ABC üçgen ADE CEB m(BEC) 110 m(ADE) Yukarıda verilenlere göre kaç derecedir? A) 20 B) 30 C) 40 D) 50 E) 60 ÇÖZÜM: ADE CEB ADE üçgeni ile CEB üçgeni eş üçgenlermiş. Bu nedenle tüm uzunlukları ve açıları birbirine eşittir. Eşitlikte harflerin sırasıyla uyumlu olarak açılar birbirine eşittir. Yani, CEB üçgenind eki E açısı ile ADE üçgenindeki D açısı birbirine eşittir. m(ADE) 110 olur. m(BDE) 180 110 70 olur. ADE CEB olduğu için, ADE üçgenindeki A açısının karşısındaki kenar ile CEB üçgenindeki C açısının karşısındaki kenar birbirine eşittir. DE BE Bu sebeple m(DBE) 70 olur. DBE üçgeninin iç açıları toplamından, m(DEB) 180 70 70 140 dir. E noktasındaki açıların toplamı 180 olması gerek – tiğinden, 4 0 110 180 30 dir. Cevap : B 2) ABC üçgen AB 9 br AE 3 br DE 5 br EC 8 br DC 8 br Yukarıda verilenlere göre, BC kaç br dir? A) 4 B) 6 C) 7 D) 8 E) 9 ÇÖZÜM: DE EC olduğu için m(EDC) m(DEC) dir. Dolayısıyla bu açıların, dış kısımları da birbirine eşittir. m(BDC) m(BEA) olur. ABE üçgeni ile BCD üçgenine dikkat edelim. İkisinin de 3 ve 8 br olan kenarları va r ve bu kenar – lar arasındaki açı aynı. Bu sebeple bu iki üçgen eştir. (Kenar – Açı-Kenar Eşliği ( )) Dolayısıyla diğer uzunluklar da birbirine eşittir. BC AB 9 br olur. Cevap: E K.A.K. 3) www.matematikkolay.net ABC ve BDE eşkenar üçgen AD 11 br AB 8 br DC 4 br Yukarıda verilenlere göre, BDC üçgeninin çevresi kaç br dir? A) 15 B) 20 C) 24 D) 27 E) 30 ÇÖZÜM: m(CBE) olsun. m(DBC) 60 olur. ABC üçgeni de eşkenar üçgen olduğundan bir iç açısı 60 dir. Bu sebeple m(ABD) olur. BDE eşkenar üçgeninin bir kenarı x br olsun. ABD üçgeni ile CBE üçgeni eştir. Çünk ü ikisinin de x ve 8 br uzunluğunda kenarları var ve arasındaki açıları (K.A.K.). Buna göre, yı gören CE 11 br olur. x 11 4 15 br olur. Ç(BCD) 8 15 4 27 br olur. Cevap : D 4) ABE ve ADC birer üçgen m(ABE) m(ACE) AD 3 br BD 5 br AE 3 br EC x br Yukarıda verilenlere göre, x kaç br dir? A) 3 B) 4 C) 5 D) 6 E) 7 ÇÖZÜM: ABE üçgeni ile ACD üçgenine dikkat edelim. A açısı ikisinde de ortak olduğu için aynıdır. B ve C açıları da birbirine eşit. İki açıları eşit oldu. B ve C açılarının karşısındaki kenarlar da birbirine eşit. AE AD 3 br Bu sebeple bu iki üçgen eştir. (Açı Kenar Açı Eşliği (A.K.A) ) AEB açısının karşısındaki kenar 8 br olduğuna göre, ADC açısının karşısındaki kenar da 8 br olmalıdır. x 8 3 5 br dir. Cevap : C 5) www.matematikkolay.net ABCD kare m(AED) 90 AF 6 br GC 3 br Yukarıda verilenlere göre, ABCD karesinin çevresi kaç br dir? A) 36 B) 44 C) 66 D) 72 E) 81 ÇÖZÜM: m(BAC) , m(EAB) olsun. 90 olur. m(AFE) olur. (AFE üçgeni) m(BGA) olur. (BGA üçgeni) m(ADE) olur. (ADE üçgeni) AFD üçgeni ile BGA üçgenine dikkat edelim. İki üçgenin de açıları 90 , , şekl indedir. Ayrıca ‘yi gören kenarları eşittir (Kareden dolayı). Dolayısıyla bu iki üçgen eştir. yı gören kenar 6 br ise, BG 6 br olur. Karenin bir kenarı 6 3 9 br olur. Karenin çevresi de 4.9 36 br olur. Cevap : A 6) ABC üçgen AD DE AB DC BD EC m(EDC) 70 m(DEC) 60 Yukarıda verilenlere göre, m(DBE) kaç derecedir? A) 5 B) 10 C) 20 D) 30 E) 40 ÇÖZÜM: m(DCE) 180 60 70 50 dir. ABD üçgeni ile DCE üçgeni eş üçgenlerdir. Çünkü üç kenarı da birbirine eşit. (Kenar Kenar Kenar Eşliği ) ABD DCE A açısı D açısına eşittir. 70 D açısı E açısına eşittir (K.K.K.) . 60 B açısı C açısına eşittir. 50 ABC üçgeninin iç açıları toplamından 70+50+m(ABC)=180 120+m(ABC)=180 m(ABC) 60 dir. m(DBE)=60 50 10 dir. Cevap: B 7) www.matematikkolay.net ABCD kare A,B,F doğrusal BF 6 br FC 10 br AE x br m(ECF) 90 Yukarıda verilenlere göre, x kaç br dir? A) 5 B) 4 C) 3 D) 2 E) 1 ÇÖZÜM: m(ECD) olsun. m(ECB) 90 olur. m(BCF) olur. EDC üçgeni ile FBC üçgenine dikkat edelim. Açıları aynı. 90 nın karşısındaki kenarlar da aynı. Çünkü karenin birer kenarını görüyorlar. Bu sebeple eş üçg enlerdir. ( ) BCF üçgeni bir 6 – 8 -10 üçgeni olduğundan karenin bir kenarı 8 br dir. ED BF 6 br dir ( nın karşısındaki kenarlar). x 8 6 2 br olur. Cevap : D A.K.A
