 Bu bölümde Sayma Konusu ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Sayma Konusu ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…










Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
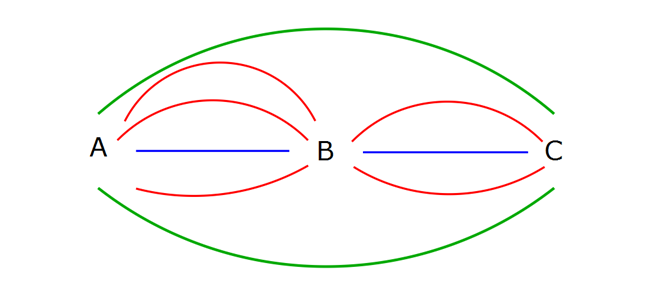
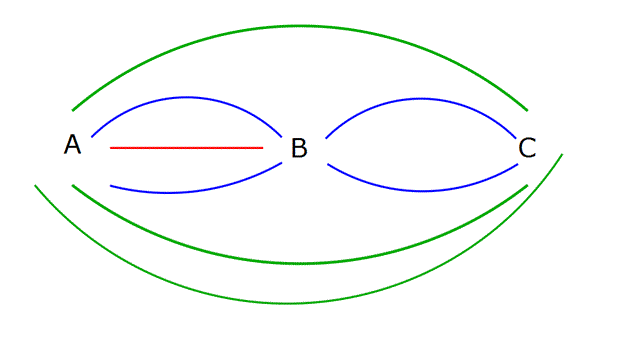
Sayma www.matematikkolay.net 1) Ahmet gittiği lokantada önüne gelen menüdeki 3 çeşit etli, 4 çeşit tavuklu ve 5 çeşit sebzeli yemekten bir tanesini kaç farklı şekilde seçebilir ? A) 3 B) 7 C) 12 D) 20 E) 60 ÇÖZÜM: Ahmet tek bir seçim yapacağı için tüm seçenekleri toplarız. 3 4 5 12 farklı şekilde seçebilir. Cevap : C 2) Serap arkadaşlarıyla buluşmaya gitmek için dolabındaki 6 bluz, 5 pantolon, 3 çanta ve 4 çift ayakkabı arasından birer seçim yaparak kombin oluşturmak istiyor. Serap buluşma için kaç farklı şekilde giyinebilir? A) 18 B) 60 C) 120 D) 360 E) 720 ÇÖZÜM: Serap her kıyafet türünden birer tane seçeceği için tüm seçenekleri çarpmalıyız. 6 5 3 4 360 bulunur. Cevap : D 3) Tatlılar İçecekler Sütlaç Çay Puding k Kahve Profiterol Soda Baklava Kola Künefe L Aslı m a g a itt o i i n t ği afede bir çeşit tatlı ve bir çeşit içecek sipariş vermek istiyor. Baklava ya da künefe yediğinde kahve içmediğine; Ve çayı sadece şerbetli tatlı- larla tükettiğine göre kaç farklı seçim yapabilir? A) 25 (Şerbetli Tatlılar: Baklava ile Künefe) B) 20 C) 15 D) 12 E) 10 ÇÖZÜM: Koşullara dikkat edelim. Çay içerse baklava ya da künefe yiyebilir. 2 durum. Kahve içerse sütlaç, puding veya profiterol yiyebilir. 3 durum. Diğer 3 içecek için tatlı sınırlaması yok. 3 5 15 durum. Topl am 2 3 15 20 şekilde sipariş verebilir. Cevap : B 4) Hüseyin bir bilgisayar uygulaması için şifre oluşturmak istiyor. Şifre 4 harf ve 2 rakamdan oluşm i alı Şifre rakamla başlayıp, rakamla bitmeli H arflerden biri büyük y za ılmalı Rakamlardan b 4 4 4 ri çift biri tek olmalı Hüseyin, şifredeki harfleri adını oluşturan harflerden seçmiştir. Kaç farklı şifre oluşturabilir ? A) 6! B) 7! C) 10 7 D) 25 7 E) 200 7 ÇÖZÜM: Rakam:R, Harf : H ile gösterilmek üzere; RHHHHR şeklinde şifreler oluşturulacak. H,Ü,S,E,Y,İ,N 7 harf 0,2,4,6,8 5 çift rakam 1,3,5,7,9 5 tek rakam var. Şifre, çift rakamla veya tek rakamla başlayabilir. Rakamlar 4 harften R R Harfler Çift Tek 1’i büyük veya Tek Çift 2 durum 4 harften 1 tanesi büyük olacak 4 durum. 2 4 5 7 7 7 7 5 4 4 8 25 7 200 7 bulunur. Cevap : E 5) Sayma www.matematikkolay.net A’dan B’ye 4 yol, B’den C’ye 3 yol ve A’dan C’ye direkt 2 yol vardır. Gidilen yolları tekrar kullanmamak şartıyla A’dan C’ye kaç farklı şekilde gidip, dönülebilir? A) 122 B) 120 C) 108 D) 98 E) 96 ÇÖZÜM: Dönüş A’dan C’ye B’ye uğrayarak giderse; 4 3 12 yoldan gider. Dönerken B’ye uğrarsa aynı yolları kullanmadan 2 3 6 yoldan döner. Dönerken direkt dönerse 2 yoldan döner. 12 (6 2) 96 yol. A’dan C’ye di Dönüş rekt 2 yoldan gider. Dönerken B’ye uğrarsa 3 4 12 yoldan döner. Dönerken direkt dönerse kulandığı yol dışında kalan 1 yolla dönebilir. 2 (12 1) 26 yol 96 26 122 yolla gidip dönebilir. Cevap : A 6) A’dan B’ye 3 farklı yol, B’den C’ye 2 farklı yol, A’dan C’ye direkt 3 farklı yol vardır. Gidilen yol aynen kullanılmamak koşuluyla kaç farklı yoldan gidilip dönülebilir? A) 96 B) 90 C) 72 D) 60 E) 54 ÇÖZÜM: Bu soruda yol kelimesine dikkat edelim. Burdaki kasıt güzergahın aynen kullanılmaması. A’dan C’ye B’ye uğrayarak 3 2 6 yoldan gider. Yine B’ye uğrayarak dönerse gidilen 6 yoldan birini kullanamaz 5 yolla döner. Direkt dönerse 3 yolla döner. 6 5 3 48 yol A’dan C’ye direkt giderse 3 yolla gider. Dönerken B’ye uğrasa 2 3 6 yolla döner. Direkt dönerse giderken kullandığı yollar dışında kalan 2 yoldan biriyle 2.Mar dönebilir. 3 6 2 24 yol 48 24 72 yolla gidip dönebilir. A’dan B’ye gitmek için 9 farklı yol var. (6 3 9) Dönerken 8 yol kullanabilir. 9.8 72 yolla gidip dönebilir. Cevap : C II.Yol : 7) A {0,1,2,3,4,8,9} kümesinin elemanları kullanılarak 3 basamaklı rakamları farklı kaç farklı çift sayı yazılabilir? A) 120 B) 100 C) 90 D) 80 E) 75 ÇÖZÜM: Sayma www.matematikkolay.net Diğer 6 rakamdan biri gele A {0,1,2,3,4,8,9} Rakamları farklı dediği için ve kümede 0 da olduğu için 0’ın durumunu ayrı inceliyeceğiz. Önce birler basamağını yerleştirerek başlıyacağız. 6 0 olursa 2 veya 4 0 dışında olursa Kalan kalan 5 0 la beraber bilir. 5 rakamdan rakamdan kalan 5 rakamdan biri geleblir. biri gelebilir. biri gelebilir. 5 1 5 5 2 30 50 80 bulunur. Cevap : D 8) A {0,1,2,3,4,5} kümesinin elemanları kullanılarak yazılabilecek 4 basamaklı sayıların kaç tanesinin en az 2 basamağı aynıdır? A) 1080 B) 960 C) 900 D) 780 E) 720 ÇÖZÜM: 0 dışındaki rakamlar tekrar edebilir tüm rakamlar 0 dışında rakamlar tekrarsız tüm rakamlar A {0,1,2,3,4,5} 4 basamaklı tüm sayılar 5 6 6 6 1080 Rakamları farklı sayılar 5 5 4 3 olduğu için azalarak ilerliyoruz.0’ı burda kullanabiliyoruz. 300 Tüm durumdan rakamları farklı olanları çıkartırırsak en az 2 rakamı aynı olanlar kalır. 1080 300 780 bulunur. Cevap : D 9) A {0,1,2,3,4,5,8} kümesinin elemanlarıyla 300’den büyük 3 basamaklı kaç farklı doğal sayı yazılabilir? A) 200 B) 196 C) 195 D) 168 E) 120 ÇÖZÜM: 3,4,5,8 rakamlar tekrar edebilir A {0,1,2,3,4,5,8} 4 7 7 196 Bu 196 sayı arasında 300 de var. 300’den büyüklerin sayısı 196 1 195 bulunur. Cevap : C 10) A {0,1,2,3,4,5,6} kümesinin elemanları ile rakamları farklı 200 den küçük kaç tek sayı yazılır? A) 33 B) 28 C) 23 D) 15 E) 10 ÇÖZÜM: Sadece 1 başa gel Burada dikkat edilmesi gereken şey basamak sayısı ile ilgili bir şey söylenmemiş. 200’den küçük bir sayı 3 basamaklı, 2 basamaklı ve 1 basamaklı olabilir. A {0,1,2,3,4,5,6} 3 basamaklı 1 ebilir. 3 ve 5 Geriye ten biri kalan gelebilir 5 rakamdan biri gelebilir. 1,3 ve 5 ten 0 ve birler biri geleiblir. basamağındaki sayı dışında kalan 5 sayıdan biri gelebiir. 5 2 10 2 basamaklı 5 3 15 1 basama klı 1,3,5 3 tane 10 15 3 28 bulunur. Cevap : B
 Bu bölümde Sayma Konusu ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Sayma Konusu ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…



















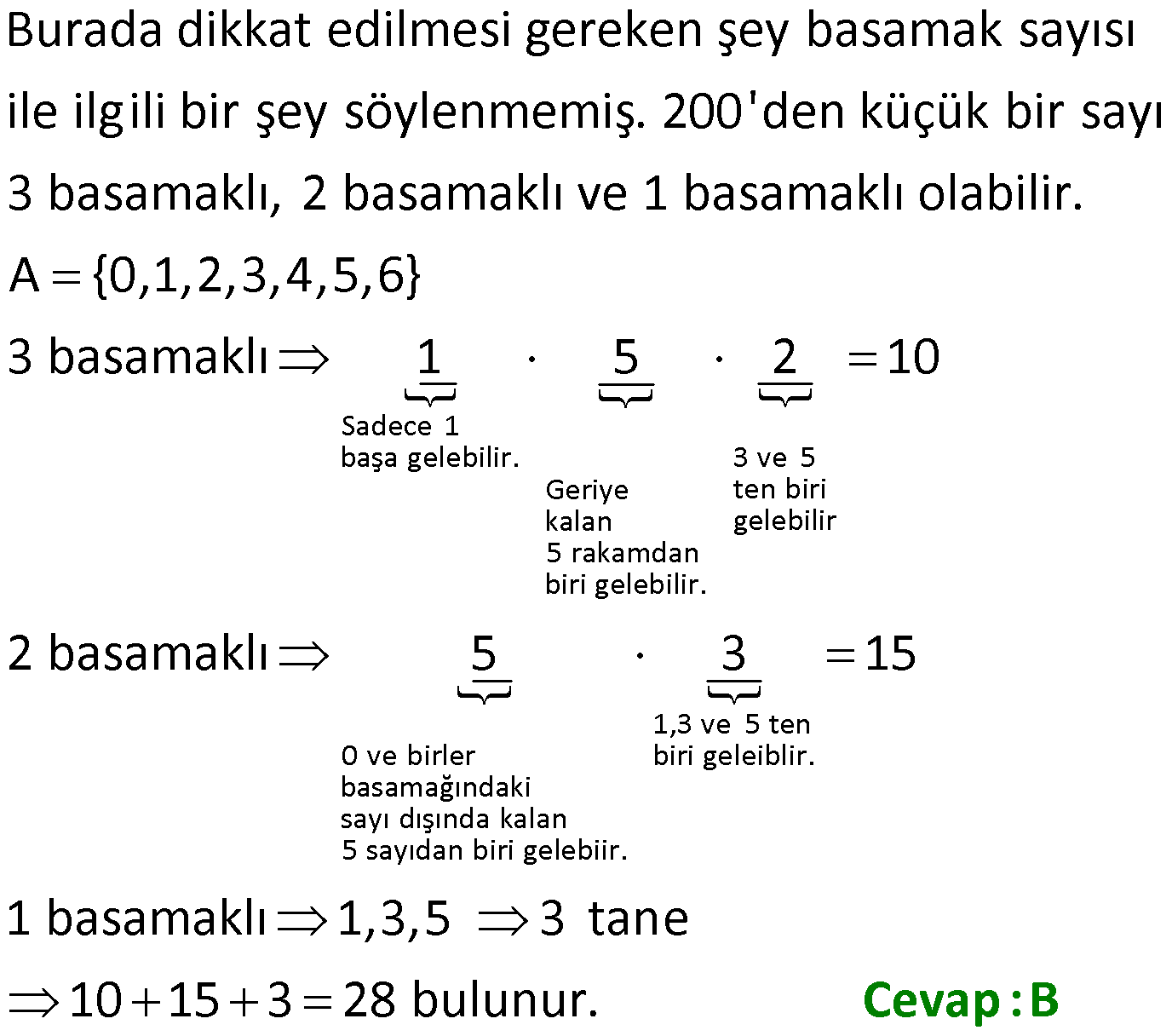



10. soruda yanlışlık var
Tekrar inceledik ama hata göremedik. 3 basamaklı olmak zorunda değil. Buna dikkat ettiniz, değil mi?
16. Soruda bir yanlışlık yok mu? Çünkü oluşturulacak kelimenin harf sayısıyla ilgili bir bilgi vermemiş. Acaba açıklayabilir misiniz? Tam anlamadım da..
Uyarınız için teşekkürler. Netlik kazanması için harf sayısını belirterek yazdık şimdi.
çok teşekkürler
Rica ederiz.
15. Soruda her soruda 4 seçenek kalması gerekmezmi
Hayır. Ard arda gelen herhangi üç sorunun cevabı aynı olmayacak denmiş. Yani bir sorunun cevabı önceki 2 soruyla aynı olamaz. Bu sebeple 3 seçenek kalır.
Faydalı oldu teşekkür ederim.
Arkadaslar Ben bazi sorulari yapamadim 10sinifim bunlar nana bi Tik Zor geldi
10.soruda yanlışlik yok mu 3 basmakli da 1 gittiğinde 6 seçenek kalıyor ama siz 5 seçenek yazmissiniz . 0 eklediğimozde 6 seçenek kalıyor 1
1’i başa yazdıktan sonra, birler basamağına rakam yazıyoruz. En son, onlar basamağına rakam koyuyoruz. O yüzden 5 seçenek kalıyor.
10. soruda sanırım bir hata var nedeni şu:
3 basmaklı ve 1 basmaklı sayıları doğru hesaplamışsınız tmmda ama 2 basamaklılarda yanlış hesaplama var soru rakamları farklı demiş siz son basamağa 1,3,5 yazmışsınız 2. basamağada sıfır hariç ve bir tane sayı 1ler basamğında kullandığı için onlar basamğına 5 yazmışsınız bu yanlış habuki bu yanlış gerçek cevap bence böyle olmalıydı;rakamları farklı dediği için 1ler basmağını ayrı incelememiz lazm yani 3 adet 2 bas. sonra bunları toplayacaktık
Çözümü tekrar inceledik ama hata göremedik.
İki basamaklı, rakamları farklı tek sayılar yine 15 tane çıkıyor. İstersen tek tek yazalım.
13, 15, 21, 23, 25, 31, 35, 41, 43, 45, 51, 53, 61, 63, 65
tşk tekrar baktım benim anlattığım çözümde doğruydu sadece ilem hatası yapmıştım ondan direk soru yanlış dedim
10.sınofım ve bu soruların neredeyse hiçbirini bilemedim. Ve sınava 3 gün var. Evettt BEN BİR MALIM..
11. soruyu anlayamadım
ok
Bazı soruları yapamıyorum. Ve sınavıma 2 gün kaldı napıcam
Abi karantinadayim k3ndim çalışmaya çalışıyorum hoca falan yok hiç birsey anlamadım bir 5ane böle soru doğru yapamadım. ağlamak :(😱
ok
geçmişler ola
sorular mükemmel teşekkür ederim