 Bu bölümde Merkezi Eğilim ve Yayılım Ölçüleri ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Merkezi Eğilim ve Yayılım Ölçüleri ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…












Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
VERİ (MERKEZİ EĞİLİM VE YAYILIM ÖLÇÜLERİ) www.matematikkolay.net 1) Gün Pzt Salı Çrş Prş Cuma Ct Pzr Saat 1 1,5 1 0,5 2 5 3 Yukarıdaki tabloda, Oğuz’un hangi gün kaç saat bilgisayar oyunu oynadığı verilmiştir. Buna göre, Oğuz günde ortalama kaç saat bilgisayar oyunu oynamaktadır? A) 1,5 B) 2 C) 2,1 D) 2,2 E) 2,5 ÇÖZÜM: 1 2 n Tüm verilerin toplamının veri sayısına bölü- müne aritmetik ortalama denir. Tüm veriler Ortalama Veri Sayısı x x … x X n Buna göre, 1 1,5 1 0,5 2 5 3 14 Ortalama= 2 saat 7 7 oyun o Not : ynamaktadır. Cevap: B 2) 30 kişilik bir sınıfın matematik sınavındaki puanı ortalama 42 dir. Eğer sınıftan ortalama puanı 30 olan 6 kişi ayrılırsa, sınıfın yeni ortalaması kaç olur? A) 45 B) 46 C) 47 D) 48 E) 50 ÇÖZÜM: 30 kişinin puanları toplamı 30.42 1260 tır. Ayrılan 6 kişinin puanları toplamı 6.30 180 dir. Geriye 1260 180 1080 puan ve 24 kişi kalır. 1080 Yeni ortalama 270 24 6 270 90 6 2 45 tir. Cevap: A 3) 9 kişilik bir grubun, bir yılda okudukları kitap sayıları 5, 2, 1, 6, 18, 11, 8, 4, 2 şeklindedir. Bu veri grubunun medyanı (ortanca) kaçtır? A) 4 B) 4,5 C) 5 D) 6,3 E) 7 ÇÖZÜM: Tüm veriler küçükten büyüğe doğru sıralandığında tam ortadaki terime ) denir. Veri sayısı çift olduğunda, tam ortadaki terim olmayacaktır. Bu durumda, ortadaki 2 terimin ortalamas Not : ortanca (medyan Medyan (Ortanca) ı alınır. Buna göre, kitap sayılarını sıralayalım. 1, 2, 2, 4, 5 , 6, 8, 11, 18 Medyan 5 tir. Cevap : C 4) 8 kişinin evlerinin hastaneye olan uzaklıkları km cinsinden, 12, 2, 4, 5, 14, 3, 16, 10 şeklindedir. Bu veri grubunun medyanı ile ortalaması arasındaki farkın mutlak değeri kaçtır? A) 0 B) 0,25 C) 0,5 D) 0,75 E) 1 www.matematikkolay.net ÇÖZÜM: 5 10 Medyan 7,5 2 Tam ortada veri olmadığı için, ortadaki iki terimin ortalaması alındı. Verileri küçükten büyüğe doğru sıralayalım. 2, 3, 4, 5, 10, 12, 14, 16 Medyan 7,5 tir. 2 3 4 5 10 12 14 1 Ortalama 6 8 66 33 8 4 8,25 tir. Fark 8,25 7,5 0,75 tir. Cevap: D 5) Sezai’nin, 10 gün boyunca topladığı fındık miktarları kg cinsinden, 75, 80, 84, 84, 78, 92, 78, 84, 76, 74 şeklindedir. Buna göre, bu veri grubunun tepe değeri (mod) kaçtır? A) 76 B) 78 C) 80 D) 84 E) 92 ÇÖZÜM: Bir veri grubunda en çok tekrar eden veriye ) denir. Tepe değeri, birden fazla olabilir. Bütün veriler eşit sayıda tekrar ediyorsa tepe değeri yoktur. Buna göre, veri grubunu incele Not : tepe değeri (mod rsek, 3 kere 84 tekrar etmiş. 3 veya 3 ten daha fazla tekrar eden bir veri yok. Bu sebeple tepe değeri 84 tür. Cevap: D 6) 2, 3, 3, 4, 5, 6, a Yukarıdaki veri grubu ile ilgili aşağıdakilerden hangisi yanlıştır? A) a 8 olursa medyan 4 olur. B) a 6 olursa bu veri grubunun iki modu olur. C) a 1 olursa medyan ile aritmetik ota lama eşit olur. D) a 3 olursa tepe değeri 3 olur. E) a 5 olursa medyan ile aritmetik otalama eşit olur. ÇÖZÜM: medyan mod mod (tepe (tepe değeri) değeri) medyan Şıkları değerlendirelim. A) 2, 3, 3, 4 , 5, 6, 8 medyan 4 olur, doğru. B) 2, 3, 3 , 4, 5, 6, 6 İki modu olur, doğru. C) 1, 2, 3, 3 , 4, 5, 6 medyan 3 olur. mod (tepe değeri) medyan 1 2 3 3 4 5 6 24 Ortalama olur. 7 7 İkisi birbirine eşit değil. C şıkkı yanlış. D) 2, 3, 3, 3, 4, 5, 6 tepe değeri 3 olur, doğru. E) 2, 3, 3, 4 , 5, 5, 6 medyan 4 olur. Ortalama 2 3 3 4 5 5 6 28 4 olur. 7 7 İkisi birbirine eşit, doğru. Cevap : C 7) 12, 10, 8, 14, 11, 5, 16, 11, 9 Veri grubunun açıklığı x, medyanı y dir. x Buna göre, oranı kaçtır? y 5 3 7 A) 1 B) C) D) E) 2 4 2 4 ÇÖZÜM: www.matematikkolay.net En En medyan küçük büyük y Veri grubunu küçükten büyüğe doğru sıralayalım. 5 , 8, 9, 10, 11 , 11, 12, 14, 16 Açıklık 16 5 11 dir x . x 11 1 dir. Cevap : A y 11 Açıklık, bir veri grubunun en büyüğü ile Not : en küçüğü arasındaki farktır. 8) 12 14 15 11 x 17 16 13 Yukarıdaki veri grubunun açıklığı 11 ise, x’in alabile – ceği değerlerin çarpımı kaçtır? A) 76 B) 98 C) 116 D) 124 E) 132 ÇÖZÜM: x değeri en büyük ya da en küçük değer olmazsa, açıklık 17 11 6 olur. Demek ki, 11 olan açıklık, x ile sağlanmalı. En büyük sayı 17 ise, 17 x 11 x 6 olmalı. En küçük sayı 11 ise, x 11 11 x 22 olm alıdır. O halde, x değerlerinin çarpımı 6.22 132 dir. Cevap : E 9) FEN LİSESİ 11, 8, 9, 6, 5, 17, 6, 3, 13 Veri grubunun çeyrekler açıklığı kaçtır? 13 15 A) 6 B) C) 7 D) E) 8 2 2 ÇÖZÜM: 1 medyandan küçük değerlerdir. medyandan büyük değerlerdir. Alt grubun medyanıdır. Üst grubun medyanıdır. Üst çeyrek ile alt çey 3 Alt grup : Üst grup : Alt çeyrek (Q ): Üst çeyrek (Q ): Çeyrekler açıklığı (Q): medyan Alt grup Üst grup 5 6 11 11 13 Alt Çeyrek Üst Çeyrek 2 2 rek arasındaki farktır. Buna göre, 3, 5, 6, 6, 8 , 9, 11, 13, 17 12 2 11 13 Çeyrekler açıklığı 12 dir. Cevap : B 2 2 10) FEN LİSESİ 2, 4, 5, x, 7, 11 Veri grubunun çeyrekler açıklığı 4 ise, x’in alabileceği değerlerin toplamı kaçtır? A) 3 B) 8 C) 11 D) 14 E) 19 ÇÖZÜM: www.matematikkolay.net 2, 4, x, 5, 7, 11 6 elemanlı bir grup olduğu için, medyan ortadaki iki sayının ortalaması olacaktır. Eğer x 5 değilse, alt ve üst grup 3’er elemanlı olacaktır. Eğer x 5 ise Üst grup 5, 7, 11 olur. Medyanı 3 7 dir.(Üst Çeyrek) Çeyrekler açıklığı 4 idi. Alt çeyrek 7 4 3 olmalıdır. O halde x 3 olmalıdır. Alt grup (2, x , 4) Eğer x 5 ise Alt grup 2, 4, 5 olur. Medyanı 4 tür.(Alt Çeyrek) Çeyrekler açıklığı 4 8 Medyan 5 idi. Üst çeyrek 4 4 8 olmalıdır. O halde x 8 olmalıdır. Üst grup (7, x , 11) Eğer x 5 ise 2,4, 5,5 ,7,11 Alt grup 2, 4 olur. Medyanı 3 tür.(Alt Çeyrek) Üst grup 7, 11 olur. Medyanı 9 dur .(Üst Çeyrek) Çeyrekler açıklığı 6 olur, 4’ü sağlamaz. O halde x 5 olamaz. Buna göre, x’in değerleri toplamı 3 8 11 dir. Cevap : C 11) 3, 1, 4, 2, 5 Veri grubunun s tandart sapması kaçtır? 10 2 3 15 A) B) 5 C) D) 2 5 E) 2 3 5 ÇÖZÜM: 2 2 2 1 2 n (x X) (x X) … (x X) S n 1 Standart sapmayı hesaplamak için, 1. Aritmetik ortalama bulunur. (X) 2. Her bir verinin aritmetik ortalaması ile farkı bulunup, kareleri toplanır. 3. Bu toplam, ve Not : 2 2 2 2 2 ri sayısının 1 eksiğine bölünür ve karekökü alınır. Çıkan sonuç, bize standart sapmayı verir. Buna göre, 3 1 4 2 5 15 X 3 tür. (Ortalama) 5 5 (3 3) (1 3) (4 3) (2 3) (5 3) S 4 0 4 1 1 4 4 10 10 dir. Cevap: A 4 2 12) 3 sene boyunca birer kez yapılan yarışmalarda, 5 kişinin aldığı puanlar, aşağıdaki şıklarda gösterilmiştir. Buna göre, en istikrarlı olan kişi hangi şıktadır? 2020 Yılı 2021 Yılı 2022 Yılı A) 7 8 9 B) 3 5 1 C) 4 4 7 D) 3 7 8 E) 3 3 5 ÇÖZÜM: www.matematikkolay.net Standart sapması az olan kişi, ortalamadan daha az sapmıştır. Bu sebeple daha istikrarlıdır. Sırasyla, s tandart sapmaları hesaplayalım. A) X 8 dir. 1 0 1 S 1 dir. 2 B) X 3 tür. 0 4 4 S 2 Not : 2 dir. C) X 5 tir. 1 1 4 S 3 tür. 2 D) X 6 dır. 9 1 4 13 S 6,5 tur. 2 2 11 E) X tür. 3 4 4 16 24 9 9 9 9 12 4 S 1,3… tür. 2 2 9 3 En az s tandart sapma A şıkkındadır. Bu sebeple en istikrarlı olan kişidir. Cevap: A
 Bu bölümde Merkezi Eğilim ve Yayılım Ölçüleri ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Merkezi Eğilim ve Yayılım Ölçüleri ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar… 




























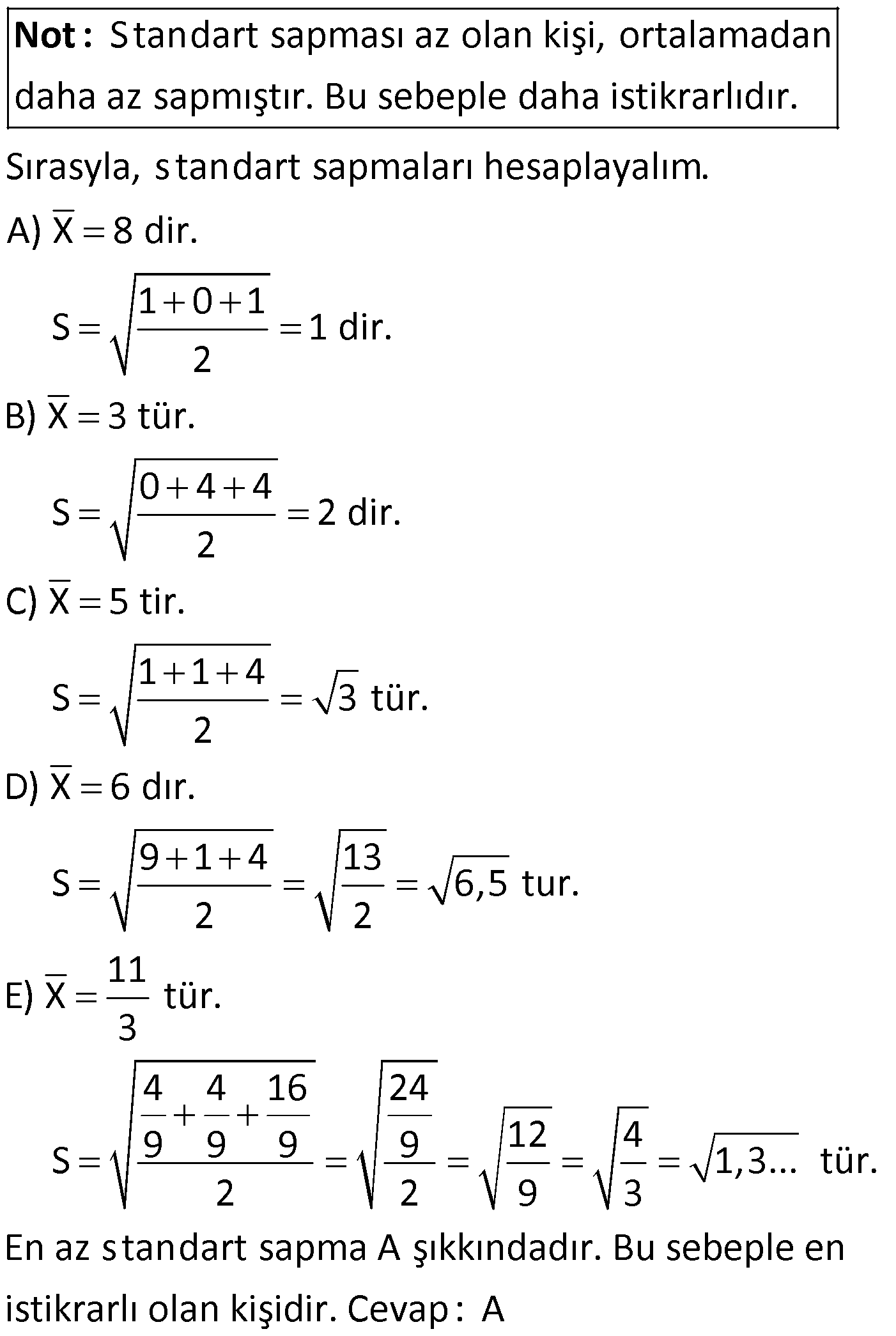



Acaba sorular hangi sınavda ne zaman çıkmış onları da yazar mısınız?
Burdaki sorular çıkmış sorular değil.
Bizim hazırladığımız sorulardır.
Çıkmış soruları telif hakları nedeniyle kullanamıyoruz.