Bu bölümde Kosinüs ve Sinüs Teoremi ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
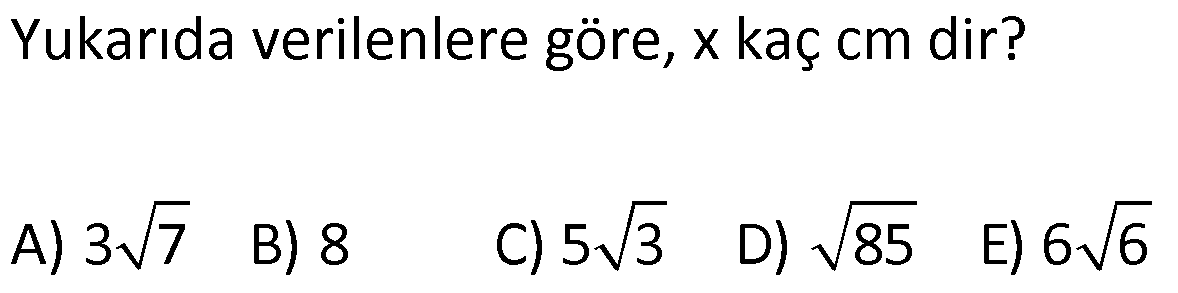
Çözüm için Tıklayınız.
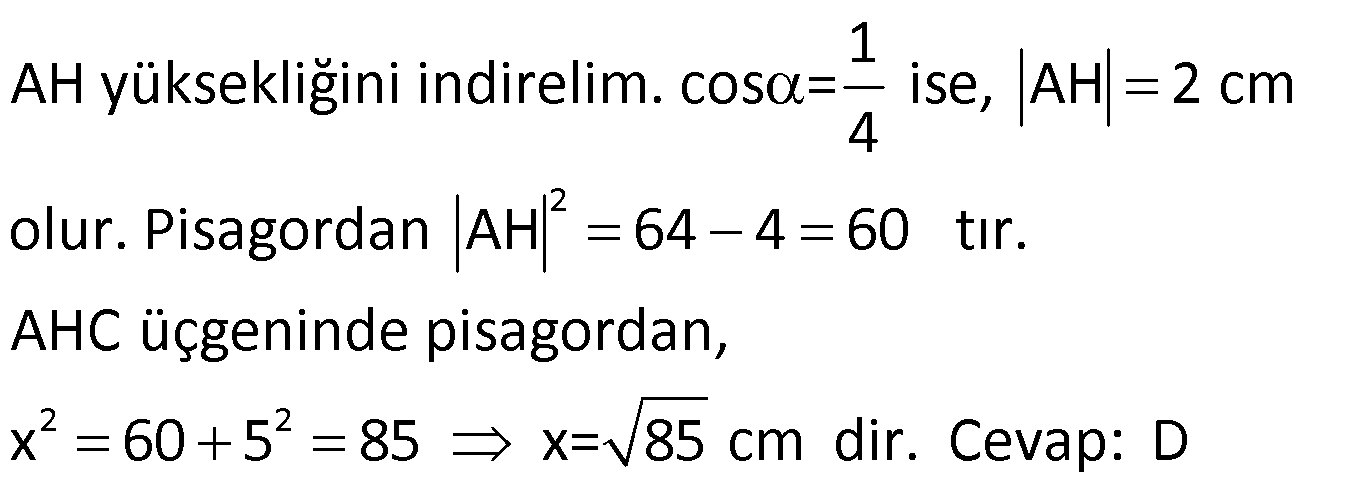
2.SORU
| | | | | |
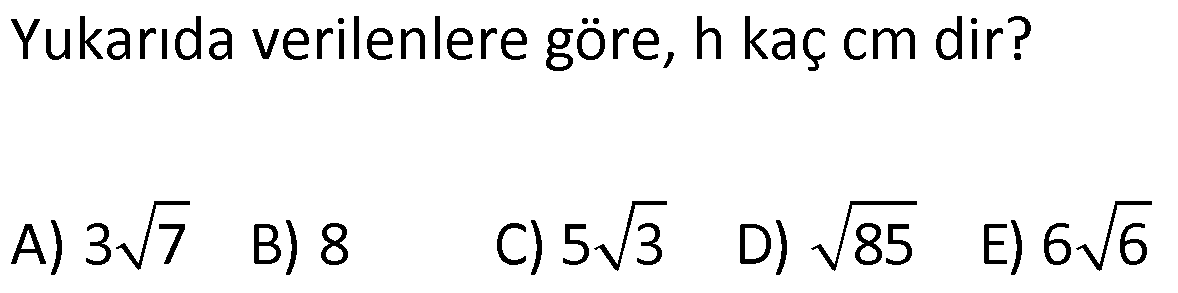
Çözüm için Tıklayınız.
3.SORU
| | | | | |
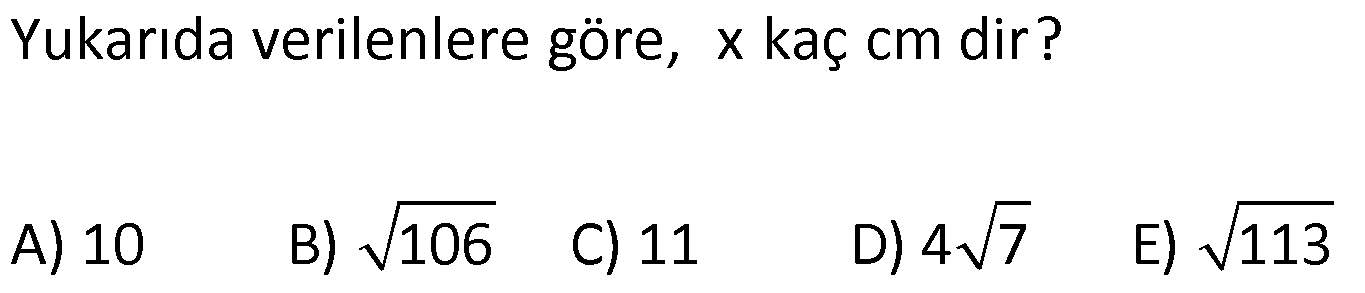
Çözüm için Tıklayınız.
4.SORU
| | | | | |
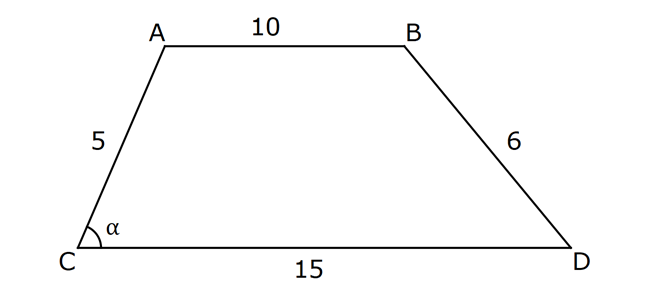
Çözüm için Tıklayınız.
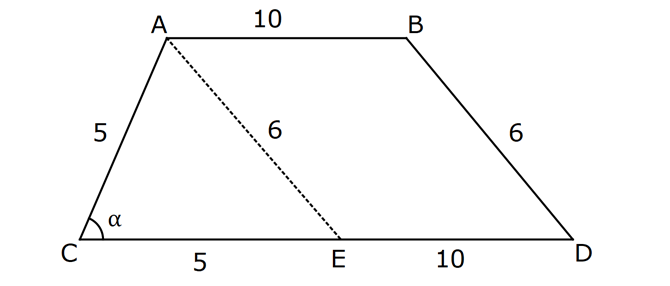
5.SORU
| | | | | |
Çözüm için Tıklayınız.
6.SORU
| | | | | |
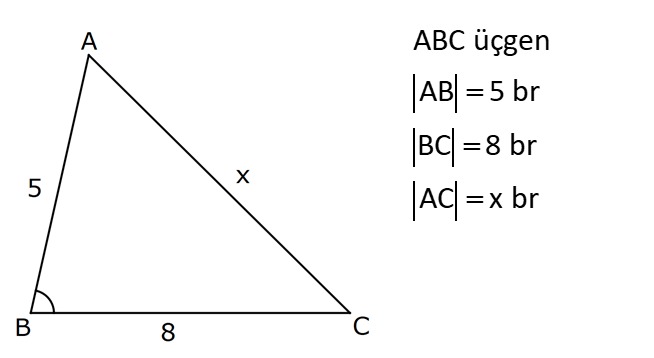
Çözüm için Tıklayınız.
7.SORU
| | | | | |
Çözüm için Tıklayınız.
8.SORU
| | | | | |
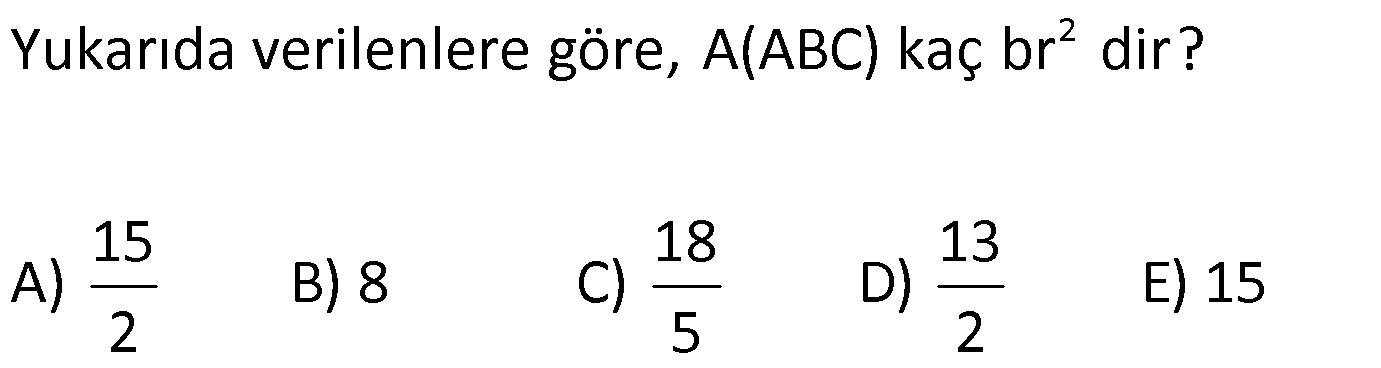
Çözüm için Tıklayınız.
9.SORU
| | | | | |
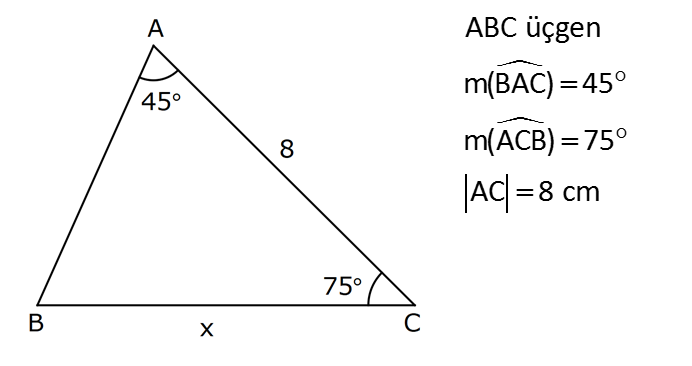
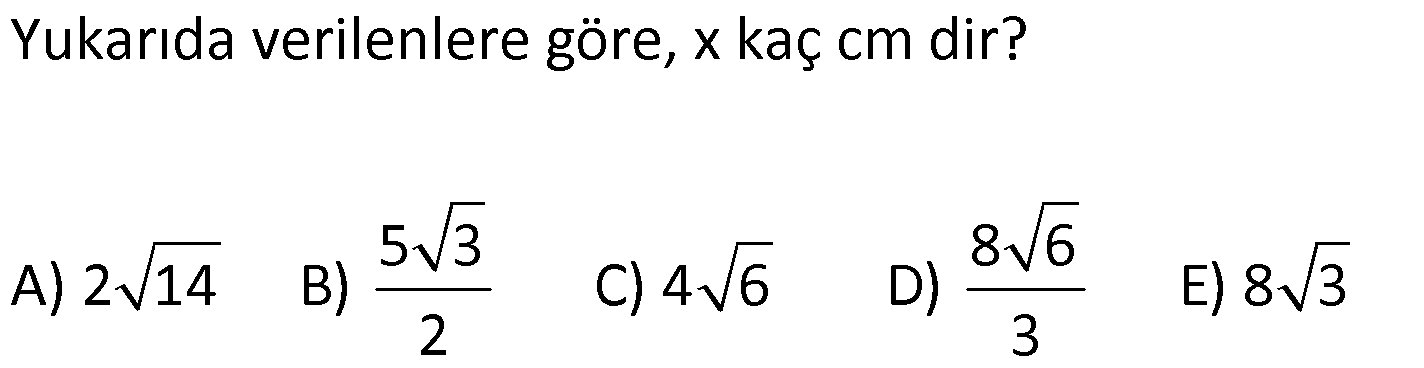
Çözüm için Tıklayınız.
10.SORU
| | | | | |
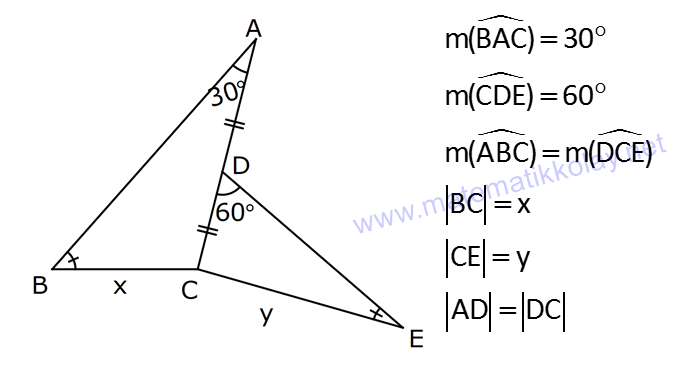
Çözüm için Tıklayınız.
11.SORU
| | | | | |
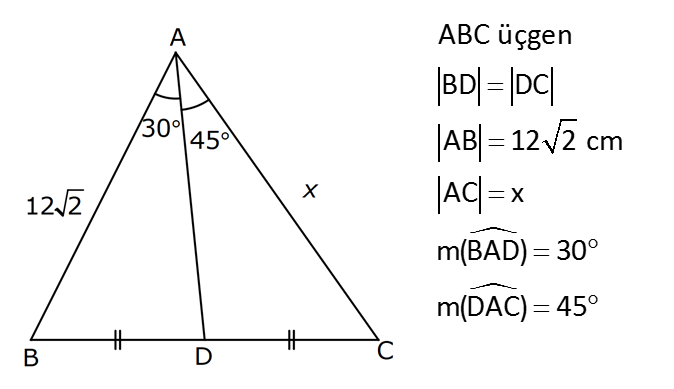
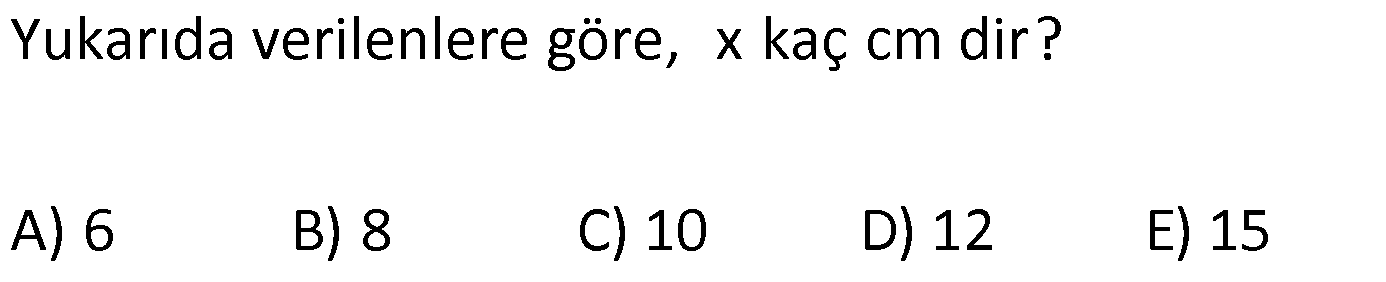
Çözüm için Tıklayınız.
12.SORU
| | | | | |
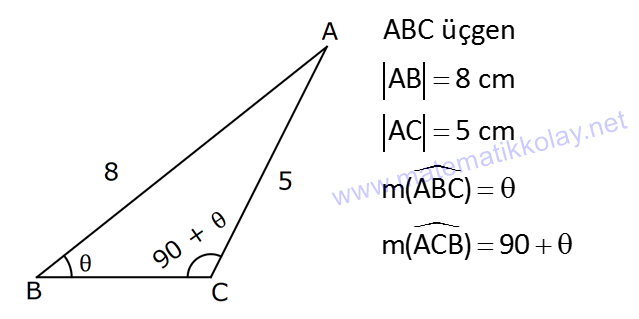
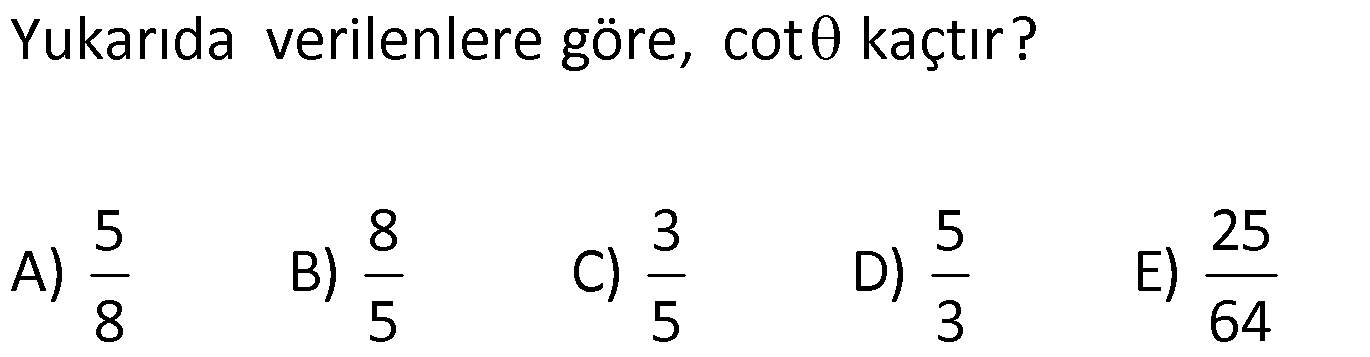
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan”Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
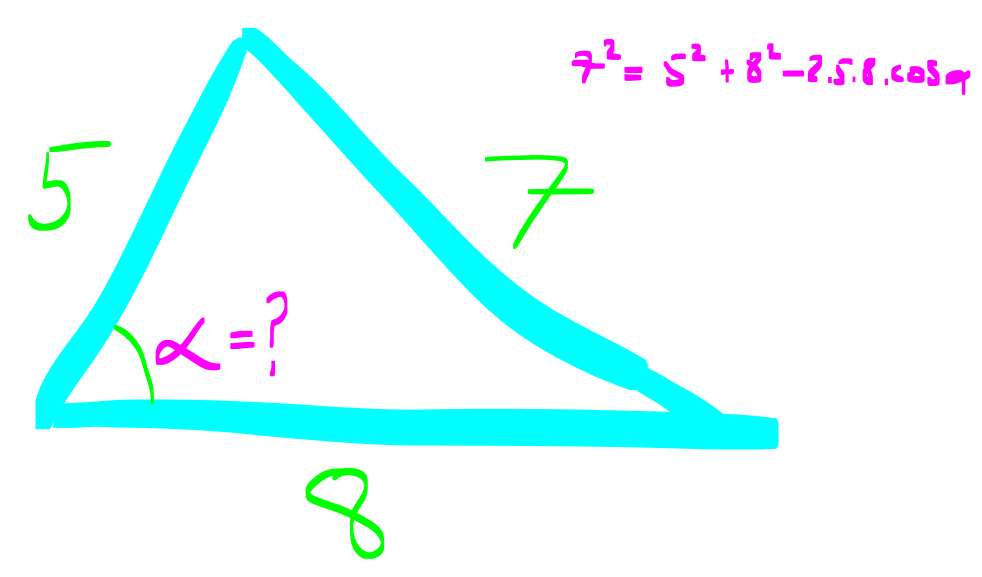
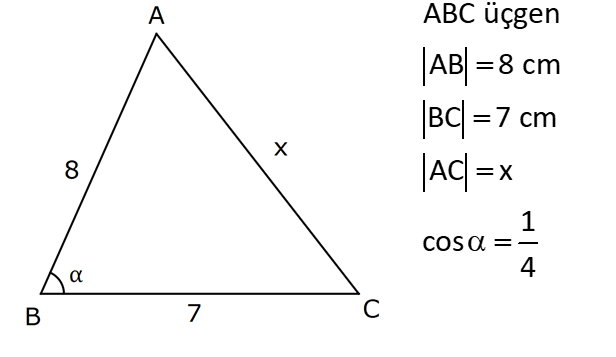
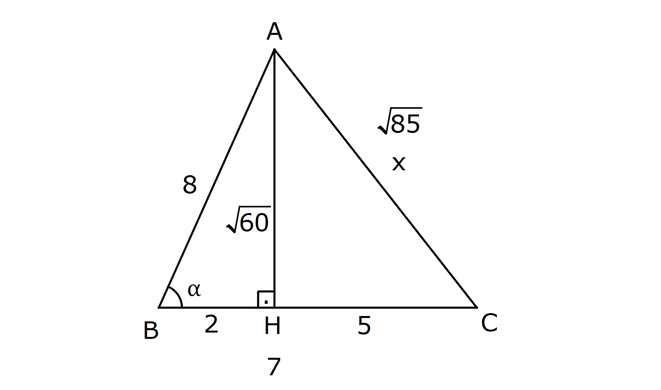
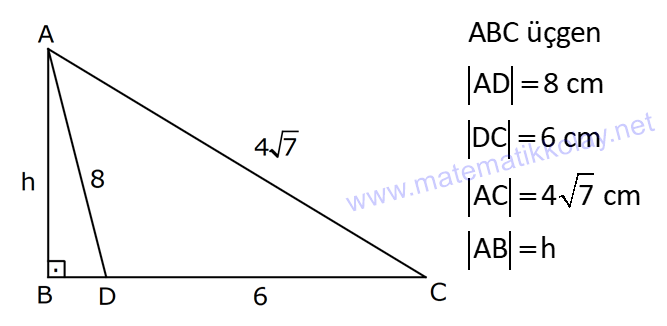
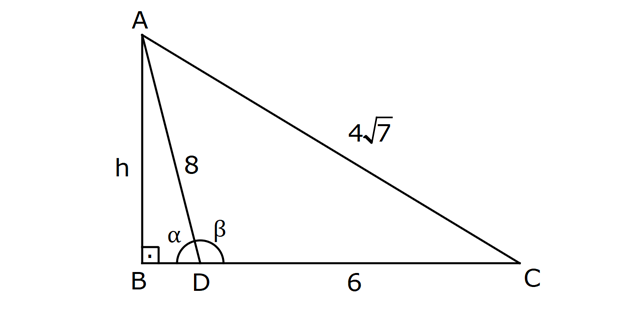
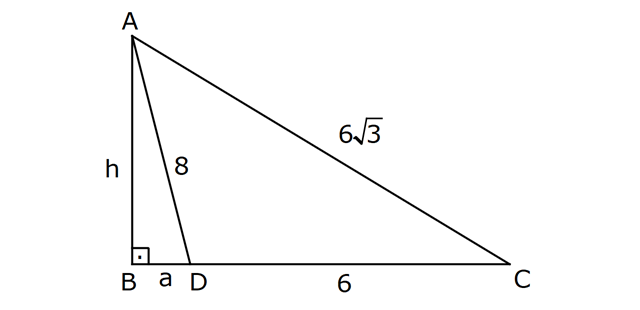
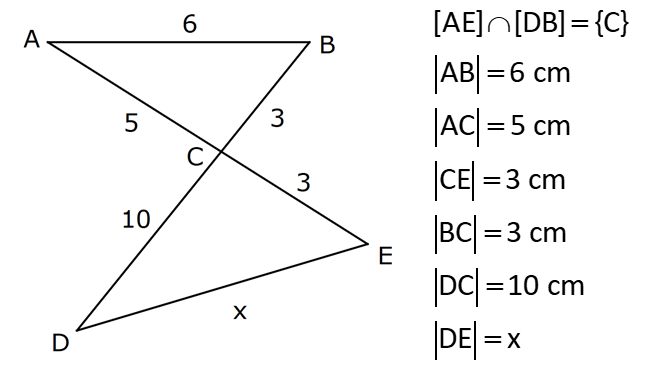
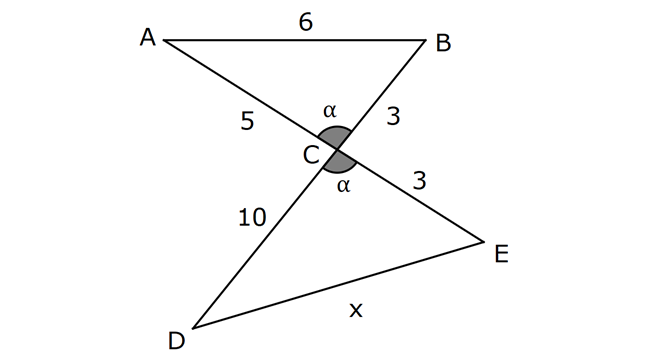
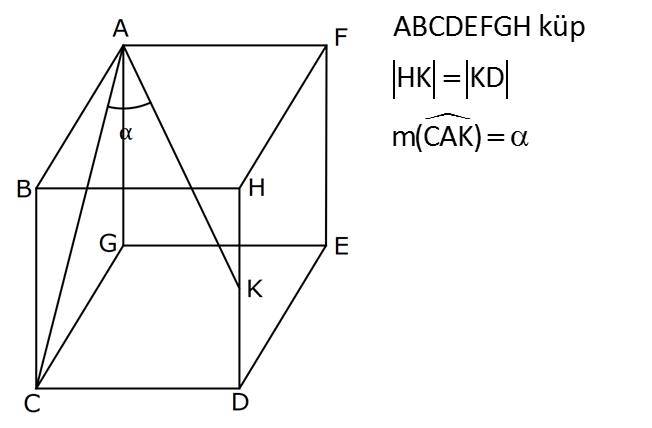
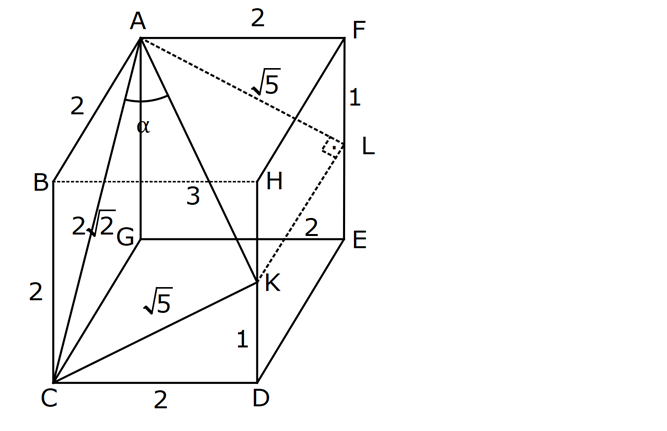
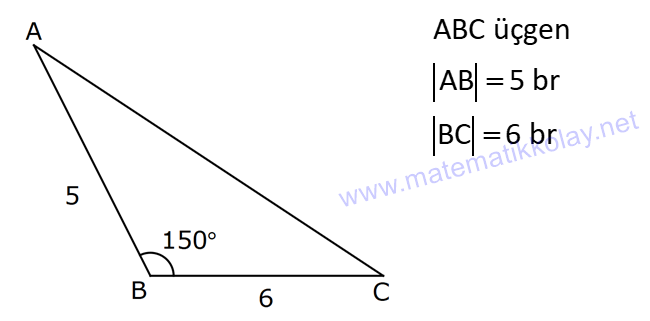
TRİGONOMETRİ -1 (11.SINIF) – (KOSİNÜS VE SİNÜS TEOREMİ) www.matematikkolay.net 1) ABC üçgen AB 8 cm BC 7 cm AC x 1 cos 4 Yukarıda verilenlere göre, x kaç cm dir? A) 3 7 B) 8 C) 5 3 D) 85 E) 6 6 ÇÖZÜM: 2 2 2 2 2 2 İki kenar ve arasındaki açının kosinüsü ile karşı kenar bulunabilir. Formülü, a b c 2.bc.cosA dır. Buna göre, x 8 7 2. 8 Not : 2 1 .7 4 2 2 x 64 49 28 x 85 x 85 cm dir. Cevap : D II.Yol: 2 2 2 1 AH yüksekliğini indirelim. cos = ise, AH 2 cm 4 olur. Pisagordan AH 64 4 60 tır. AHC üçgeninde pisagordan, x 60 5 85 x= 85 cm dir. Cevap: D 2) ABC üçgen AD 8 cm DC 6 cm AC 4 7 cm AB h Yukarıda verilenlere göre, h kaç cm dir? A) 3 7 B) 8 C) 5 3 D) 85 E) 6 6 ÇÖZÜM: 2 2 2 2 2 ADC üçgeninde kosinüs teoremi yaparak cos yi bulabiliriz. 4 7 8 6 2.8.6.cos 112 64 36 96.cos 12 96.cos 1 cos dır. 8 1 1 BD cos dir. BD 1 cm dir. 8 8 8 h 8 1 64 1 63 3 7 cm dir. Cevap : A II.Yol: www.matematikkolay.net 2 2 2 2 2 2 2 ABD üçgeninde pisagor h a 64 ABC üçgeninde pisaogr h (a 6) 112 Yukarıdaki eşitlikten, alttakini çıkarırsak (a 6) a 48 kalır. a 2 12a 36 a 2 48 12a 12 a 1 cm dir. h 8 1 63 3 7 cm dir. Cevap : A 3) [AE] [DB] {C} AB 6 cm AC 5 cm CE 3 cm BC 3 cm DC 10 cm DE x Yukarıda verilenlere göre, x kaç cm dir? A) 10 B) 106 C) 11 D) 4 7 E) 113 ÇÖZÜM: 2 2 2 2 2 2 2 2 2 ACB üçgeninden cos yı bulabiliriz. 6 5 3 2.5.3.cos 36 25 9 30.cos 36 34 30.cos 2 30cos 1 cos dır. Şimdi bunu CDE üçgeninde kulla – 15 nalım. x 10 3 2.10.3.cos 1 x 100 9 60 15 x 100 9 4 x 113 x 113 cm dir. Cevap: E 4) AB // CD ve AB 10 cm, AC 5 cm, BD 6 cm ve CD 15 cm olan ABCD yamuğunda cos kaçtır? 5 7 3 15 11 A) B) C) D) E) 6 25 4 17 15 ÇÖZÜM: www.matematikkolay.net 2 2 2 BD ye paralel olarak AE yi çizelim. AE 6 cm ve ED 10 cm olur. ACE üçgeninde kosinüs teoremini uygularsak, 6 5 5 2.5.5.cos 36 25 25 50.cos 36 50 50cos 14 50cos 7 cos dır. Cevap : B 25 5) 2 2 Bir ABC üçgeninin iç açılarının ölçüleri A, B ve C açı – larıdır ve karşısındaki kenarlar sırasıyla a, b ve c kenarlarıdır. b (a c) ac olduğuna göre, B açısı kaç derecedir? A) 30 B) 45 C) 60 D) 90 E) 120 ÇÖZÜM: 2 2 2 2 2 2 2 Kosinüs teoremine göre, b a c 2.a.c.cosB dir. Soruda verilen ifadeyle eşitleyelim. (a c) ac a c 2.a.c.cosB a 2 2ac c 2 ac a 2 c 2.a.c.cosB ac 2. ac .cosB 1 cosB dir. 2 1 0 ile 180 arasında kosinüsü olan açı 120 dir. 2 Cevap : E 30 45 60 120 135 150 3 2 1 1 2 3 cos 2 2 2 2 2 2 NOT : 6) ABC üçgen AB 5 br BC 8 br AC x br B açısı 60 den büyük olduğuna göre, x’in alabileceği kaç farklı tam sayı değeri vardır? A) 3 B) 4 C) 5 E) 6 D) 7 ÇÖZÜM: 2 2 2 2 2 2 B açısı 60 olsaydı, kosinüs teoremine göre x 5 8 2.5.8.cos60 1 x 25 64 80 2 x 89 40 x 49 x 7 olurdu. B açısı 60 den büyük olduğu için x 7 dir. Üçgen eşitsizliğine göre, x 5 8 x 13 tür. O halde, 7 x 13 x 8,9,10,11,12 5 tam sayı değeri vardır. Cevap: C 7) ABCDEFGH küp HK KD m(CAK) www.matematikkolay.net Yukarıda verilenlere göre, kaç derecedir ? A) 15 B) 30 C) 45 D) 60 E) 75 ÇÖZÜM: 2 2 2 2 Rahat işlem yapmak için, küpü bir ayrıtı 2 cm olsun. CDK dik üçgeninde, CK 1 2 5 cm olur. FE nin orta noktası L olsun. KL 2 cm olur. AL 5 cm olur. ALK dik üçgeninden, AK 2 5 3 cm olur. ABC üçgeninden, A 2 2 2 C 2 2 cm olur. ACK üçgeninde kosinüs teoremini uygularsak, 5 2 2 3 2.2 2.3.cos 5 8 9 12 2.cos 5 17 12 2.cos 12 12 2.cos 1 cos 45 dir. Cevap: C 2 8) ABC üçgen AB 5 br BC 6 br 2 Yukarıda verilenlere göre, A(ABC) kaç br dir? 15 18 13 A) B) 8 C) D) E) 15 2 5 2 ÇÖZÜM: 2 İki kenar ve aradaki açının sinüsünden üçgenin 1 alanını bulabiliriz. A a.c.sinB 2 Buna göre, 1 1 1 15 A(ABC) 5.6.sin(150) 5.6 br dir. 2 2 2 2 Cevap : A 30 45 60 120 135 150 1 2 3 3 2 1 sin 2 2 2 2 2 2 Not : Not : 9) ABC üçgen m(BAC) 45 m(ACB) 75 AC 8 cm Yukarıda verilenlere göre, x kaç cm dir? 5 3 8 6 A) 2 14 B) C) 4 6 D) E) 8 3 2 3 ÇÖZÜM: www.matematikkolay.net Üçgenin kenarları, karşısındaki açının sinüsleri orantılıdır. a b c dir. sinA sinB sinC B açısı 60 dir. 8 x 8 sin60 sin45 3 2 Not : x 2 2 3 8 2 x 3 8 6 x cm dir. Cevap : D 3 10) m(BAC) 30 m(CDE) 60 m(ABC) m(DCE) BC x CE y AD DC x Yukarıda verilenlere göre, oranı kaçtır? y 3 2 1 3 2 3 A) B) C) D) E) 2 3 2 4 3 ÇÖZÜM: CDE üçgeninde sinüs teoremini uygulayalım. DC y y.sin y.sin 2ysin DC sin sin60 sin60 3 3 2 2ysin 4ysin AC 2. DC 2 tür. 3 3 ABC üçgeninde sinüs teoremini uygulayalım. 4y sin x x AC sin30 sin 1 2 3 sin 2 4 x 2 3 y 3 x 2 2 3 tür. Cevap : E y 3 3 11) ABC üçgen BD DC AB 12 2 cm AC x m(BAD) 30 m(DAC) 45 Yukarıda verilenlere göre, x kaç cm dir? A) 6 B) 8 C) 10 D) 12 E) 15 ÇÖZÜM: www.matematikkolay.net BD DC olduğundan, A(ABD) A(ADC) dir. 1 2 12 2 AD 1 sin30 2 AD x sin45 12 2 1 2 2 x 2 12 x tir. Cevap : D 12) ABC üçgen AB 8 cm AC 5 cm m(ABC) m(ACB) 90 Yukarıda verilenlere göre, cot kaçtır? 5 8 3 5 25 A) B) C) D) E) 8 5 5 3 64 ÇÖZÜM: 2.bölgede sin dır. (fonksiyonun adı değişir.) ABC üçgeninde sinüs teoremini uygularsak, 8 5 8 5 sin 90 sin cos sin 8 cos 8 cot tir. Cevap: B 5 sin 5
burasi olmasaydi ders boş geçecekti