Bu bölümde Kartezyen Çarpım ile ilgili 10 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
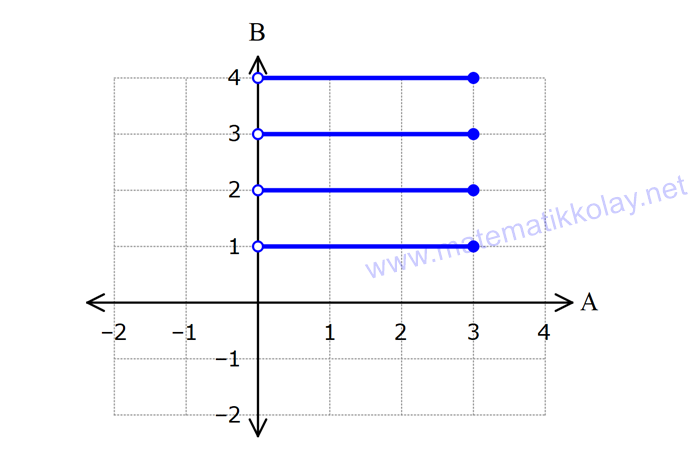
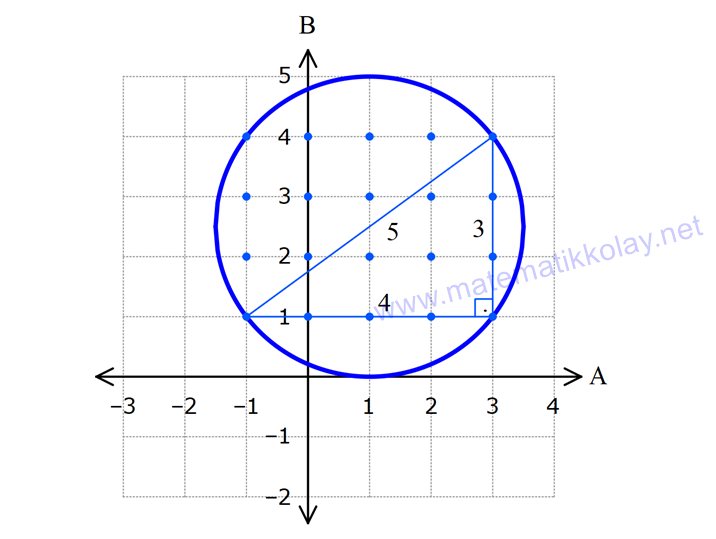
KARTEZYEN ÇARPIM www.matematikkolay.net 1) (3x 2y, 3) (4, x y) olduğuna göre, x.y kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: 2 3x 2y 4 2 / x y 3 tür. 3x 2y 4 2x 2y 6 5x 10 x 2 dir. x y 3 y 1 dir. O halde, x.y 2.1 2 dir. C 1.bileşen 2.bileşen evap : B a A, b B olmak üzere (a, b) şeklinde oluşturulan ikililere sıralı ikili denir. ( a , b ) sıralama değişirse, yeni bir ikili oluşur. Yani (a, b) (b, a) dir. Eğer iki tane sıra Not : lı ikili birbirine eşitse, 1.bileşenler birbirine, 2.bileşenler de birbirine eşittir. Yani, (a, b) (x, y) ise a x ve b y dir. 2) y 2 x 16, 81 x , 3 olduğuna göre, x y nin en küçük değeri kaçtır? A) 5 B) 3 C) 1 D) 3 E) 5 ÇÖZÜM: 2 y x xy 4 x 16 ise x 4 ya da x 4 tür. 3 81 3 3 xy 4 tür. x 4 olursa y 1 olur. x 4 olursa y 1 olur. x y 4 ( 1) 5 olur, en az. Cevap: A 3) A {a, b, c} B {x | 1 x 4, x Z } kümeleri veriliyor. A B kümesi aşağıdakilerden hangisinde doğru gösterilmiştir? A) {(a, b), (1, 3), (2, 2)} B) {(a, a), (b, b), (1, 1), (2, 2), (3, 3)} C) {(a, b), (1, 2, 3)} D) {(a, 2), (a, 3), (b, 2), (b, 3), (c, 2), (c, 3)} E) {(1, a), (1, b),(2, a), (2, b), (3, a), (3, b)} www.matematikkolay.net ÇÖZÜM: A {a, b, c} B {2, 3} tür. A B kartezyen çarpımında sıralı ikililerin birinci bileşeni A kümesinden, ikinci bileşeni de B kümesinden oluşacaktır. Buna göre, tüm ikilileri yazalım. (a, 2), (a, 3), (b, 2), (b, 3), (c, 2), (c, 3) tür. Bu elemanlar, D şıkkında doğru gösterilmiştir. Cevap : D A ve B boş olmayan iki küme olsun. a A ve b B olmak üzere (a, b) sıralı ikililerin tamamını bulunduran kümeye A ve Not : B kümelerinin kartezyen çarpımı denir. Ya da kısaca A kartezyen B denir. A B şeklinde gösterilir. A B {(x, y)| x A, y B} şeklinde de tanımlayabiliriz. A B değilse, A B ile B A birbirinden farklıdır. B 2 oş küme ile yapılan kartezyen çarpım, yine boş kümedir. A veya A dir. A A kartezyen çarpımı da A olarak gösterilebilir. 4) A B {(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,2),(3,3),(3,4)} kartezyen çarpımı veriliyor. Buna göre, s(A B) kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 ÇÖZÜM: Birinci bileşenler A kümesinin elemanlarıdır. A {1, 2, 3} tür. İkinci bileşenler B kümesinin elemanlarıdır. B {2, 3, 4} tür. s(A) 3, s(B) 3 tür. (A B) {2, 3} tür. s(A B) 2 dir. O halde, s(A B) 3 3 2 4 tür. Cevap : B 5) A B {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)} C D {(0, a), (0, b), (0, c), (1, a), (1, b), (1, c)} kartezyen çarpımları veriliyor. Buna göre, aşağıdakilerden hangisi (B C) A kümesinin elemanları n – dan biridir? A) (x, 1) B) (1, 2) C) (x, a) D) (2, a) E) (1, z) ÇÖZÜM: A {x, y, z} B {1, 2} C {0, 1} D {a, b, c} dir. B C {1} dir. (B C) A kartezyen çarpımı {1} {x, y, z} {(1, x), (1, y), (1, z)} olacaktır. E şıkkındaki sıralı ikili, bu kümenin bir elemanıdır. Cevap : E 6) A {x| x 12, x N} B {x| x asal sayıdır.} C {x| 12 x 60, x 3k, x N} kümeleri veriliyor. Buna göre, (A B) C kümesinin eleman sayısı kaçtır? A) 75 B) 90 C) 105 D) 120 E) 150 www.matematikkolay.net ÇÖZÜM: A B kümesi 12’den küçük, asal sayı olmayan doğal sayılardır. Bunlar 0, 1, 4, 6, 8, 9, 10 dur. Eleman sayısı 7 dir. C kümesi 15, 18, …, 57 dir. 57 15 Terim Sayısı 1 15 tir. 3 O halde, s((A B) C) s(A B) 2 .s(C) 7.15 105 tir. Cevap: C s(A) a, s(B) b olsun. s(A B) a.b dir. s(B A) b.a dır. Yani s(A B) ile aynıdır. s(A A) a.a a dir. Not : 7) s(A B) 45 s(A C) 35 tir. Buna göre, s(A A) nın alabileceği en büyük değer m, s(B C) nin en küçük değeri n dir. Buna göre, n m kaçtır? A) 10 B) 15 C) 27 D) 32 E) 38 ÇÖZÜM: 2 2 3.5 5.7 s(A) a, s(B) b, s(C) c olsun. a.b 45 a.c 35 tir. s(A A) a.a a dir. En büyük olması için a’yı büyük seçmeliyiz. EBOB(45, 35) 5 tir. a en fazla 5 olabilir. s(A A) 5.5 25 olur. m 25 tir. s(B C) nin en 5 5 küçük değeri için b ve c küçük olmalıdır. Bunun için de yine a değeri en büyük olmalıdır. a.b 45 b 9 olur. a.c 35 c 7 olur. s(B C) 9.7 63 olur, en az. n 63 O halde, n m 63 25 38 buluruz. Cev ap : E 8) A {x| x 90, x 3k, x Z} B {x| x 10, x 2k, x Z} C {x| 4 x 6, x N} kümeleri veriliyor. Buna göre, (A C) (B C) kümesinin eleman sayısı kaçtır? A) 65 B) 70 C) 78 D) 90 E) 102 www.matematikkolay.net ÇÖZÜM: (A C) (B C) (A B) C dir. A B kümesi de 10 ile 90 arasındaki hem 2’nin hem de 3’ün katı olan tam sayılardan oluşur. Yani 6’nın katı olan sayıları bulacağız. 84 12 72 Terim Sayısı 1 1 13 tür. 6 6 s(A B) 13 tür. C kümesinin elemanları ise 0, 1, 2, 3, 4, 5 tir. s(C) 6 dır. şimdi s (A B) C yi bulabiliriz. s(A B) s(C) 13.6 78 dir. Cevap : C Kartezyen çarpımının; Birleşim, kesişim, fark işlem – leri üzerine Not : dağılma özelliği vardır. A (B C) (A B) B C) A (B C) (A B) B C) A (B C) (A B) (B C) dir. 9) Yukarıdaki grafikte A B nin grafiği verilmiştir. Buna göre, A ve B kümeleri aşağıdakilerden hangisi olabilir? A) A {x| 0 x 3, x R} B) A {x| 0 x 3, x Z} B {x| 1 x 4, x Z} B {x| 1 x 5, x R} C ) A {x| 0 x 3, x Z} D) A {x| 0 x 3, x R} B {x| 0 x 5, x Z} B {x| 1 x 5, x Z} E) A {x| 0 x 4, x R} B {x| 1 x 5, x Z} ÇÖZÜM: Grafikte x değerleri, 0 ile 3 arasındaki tüm değerleri içermektedir. Ayrıca 3 de dahil edilmiştir. O halde A kümesi (0, 3] aralığından oluşmalıdır. Sadece tam sayılar dersek, eksik belirtmiş oluruz. y değerleri ise 1, 2, 3 ve 4 tam sayılarından oluşmak – tadır. Bu sebeple B {1, 2, 3, 4} kümesini ifade etmelidir. Buna uygun olarak ifade edilen kümeler, D şıkkında vardır. Cevap: D A B kartezyen çarpımının elemanları, koordinat sisteminde gösterilirken, A’nın elemanları x eksenindeki değerleri, B’nin elemanları y eksenindeki değer – leri ifade eder. Ör Not : nek : (2, 3) sıralı ikisi, x 2 ve y 3 olan bir noktayı ifade eder. 10) 2 A {x| 1 x 3, x Z} B {x| 1 x 4, x N} kümeleri veriliyor. A B kümesinin elemanlarını içeren en küçük dairenin alanı kaç br dir ? 25 15 A) 5 B) C) D) 10 E) 25 4 2 ÇÖZÜM: A { 1, 0, 1, 2, 3} tür. B {1, 2, 3, 4} tür. A B nin grafiğini aşağıdaki gibi gösterebiliriz. www.matematikkolay.net En uzak noktalar arası mesafeyi, bir dik üçgen yardı – mıyla hesaplayabiliriz. Burdaki dik üçgen bir 3- 4 – 5 üçgenidir. Yani en uzak mesafe 5 birimdir. Çemberin de çapı en az 5 br olmalıdır. 5 Yarıçapı br ol 2 2 2 2 ur. 5 25 Alanı .r br olur. Cevap : B 2 4
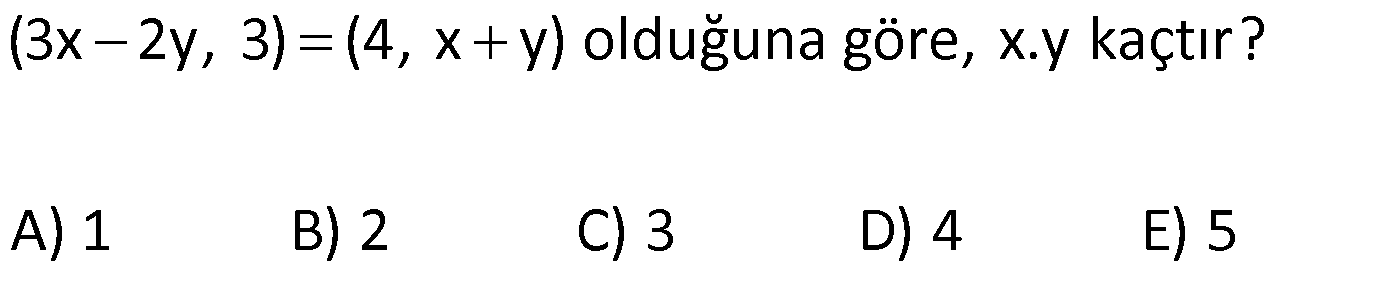
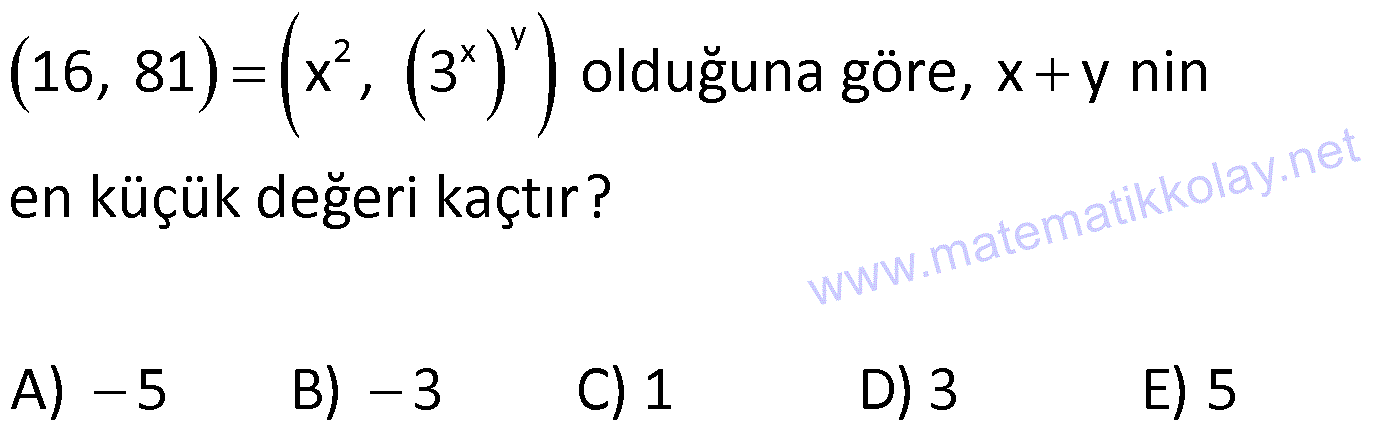
Çok iyi gercekten tesekurler oğrenci oldugum icin cokkkkkkk sansliyim