Bu bölümde Fonksiyon Uygulamaları ile ilgili 10 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
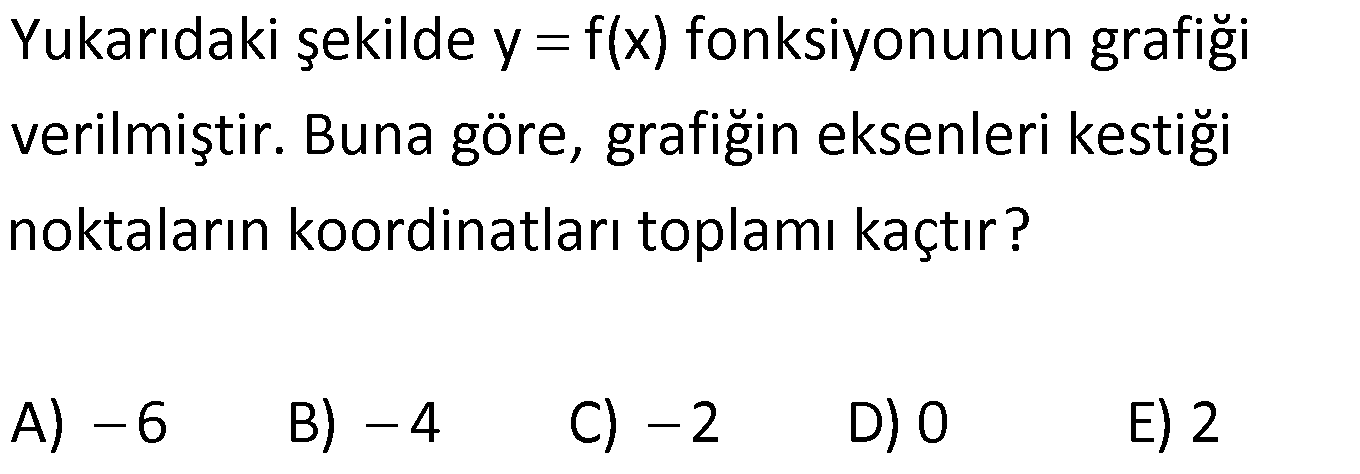
| | | | | |
Çözüm için Tıklayınız.

2.SORU

| | | | | |
Çözüm için Tıklayınız.

3.SORU

 | | | | |
Çözüm için Tıklayınız.

4.SORU

| | | | | |
Çözüm için Tıklayınız.

5.SORU

| | | | | |
Çözüm için Tıklayınız.

6.SORU

| | | | | |
Çözüm için Tıklayınız.

7.SORU
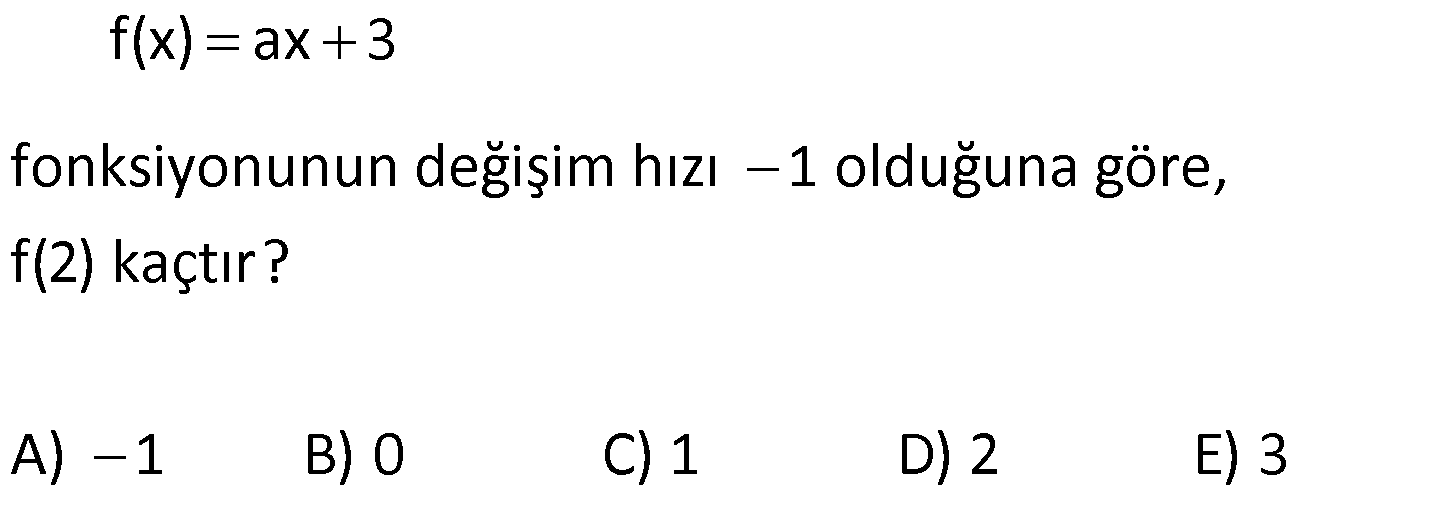
| | | | | |
Çözüm için Tıklayınız.

8.SORU

| | | | | |
Çözüm için Tıklayınız.

9.SORU

| | | | | |
Çözüm için Tıklayınız.
10.SORU
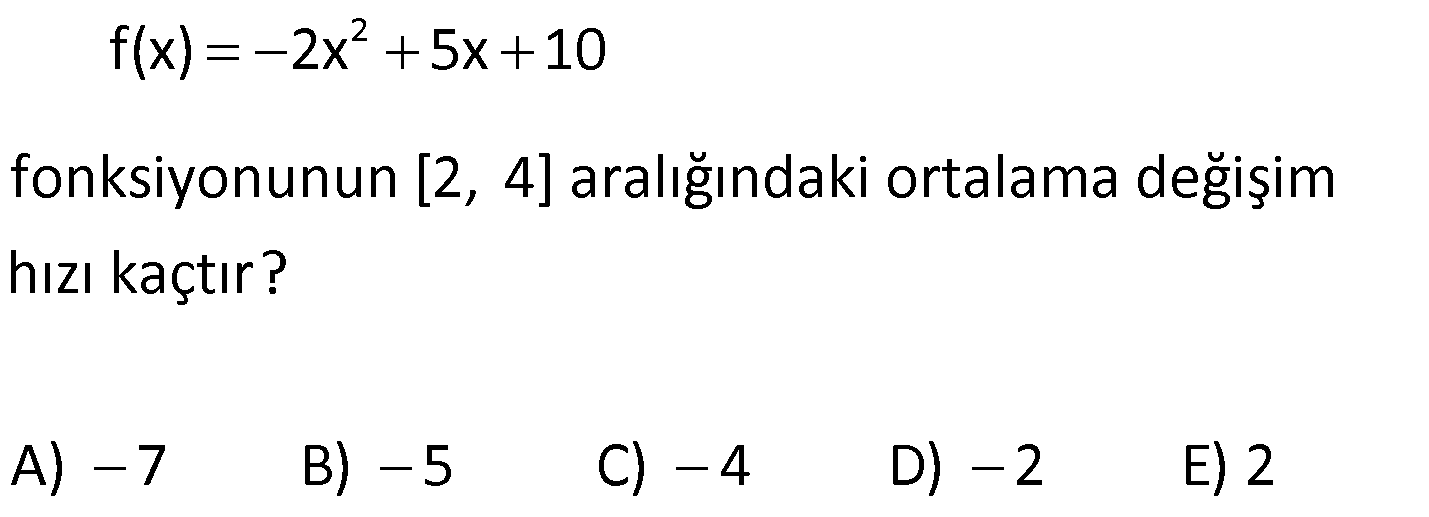
 | | | | |
Çözüm için Tıklayınız.
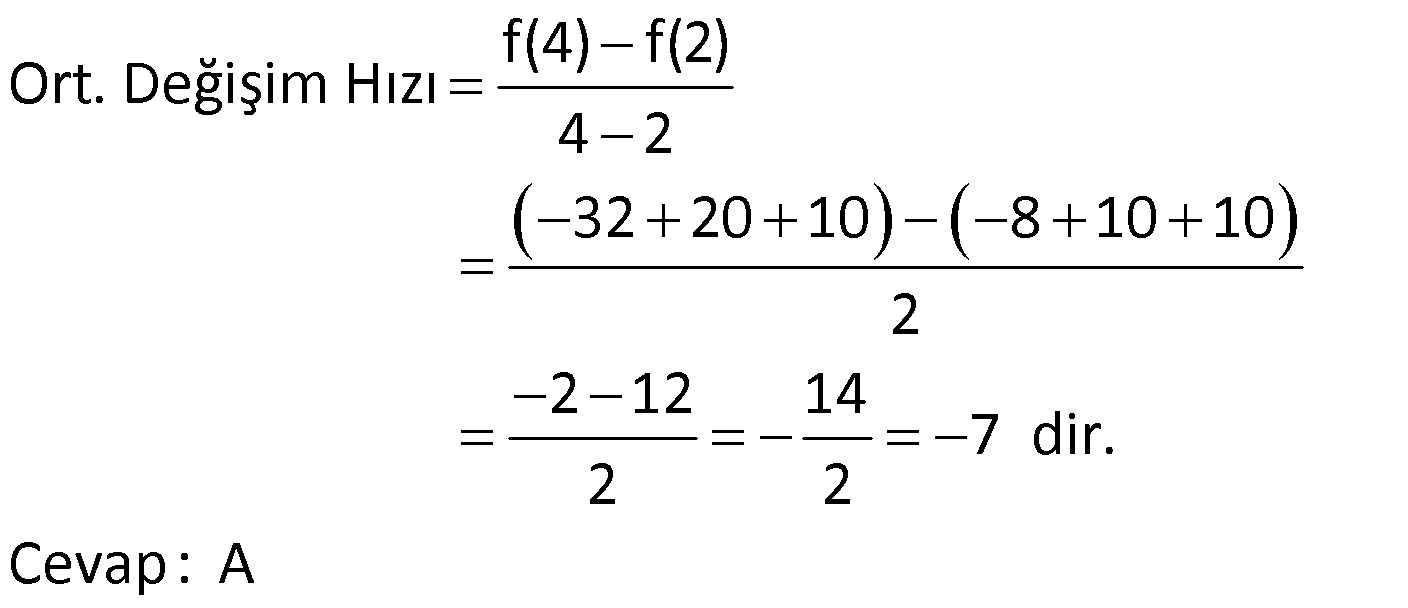
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
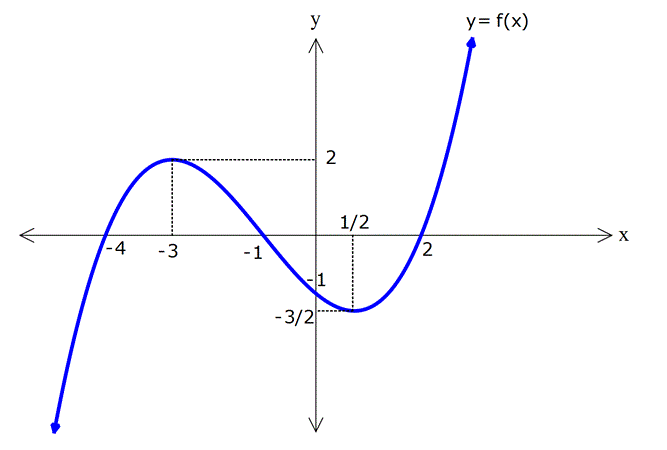
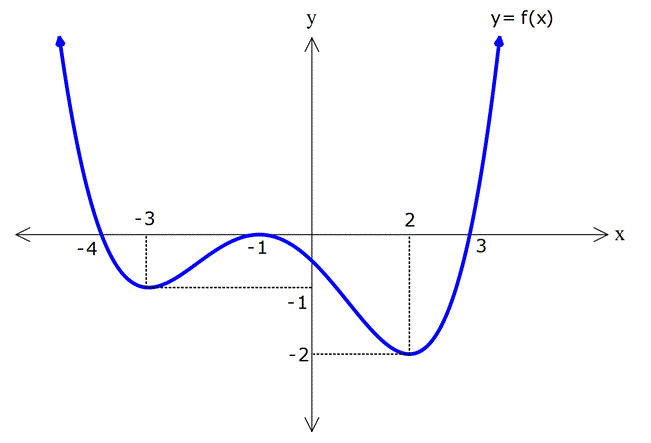
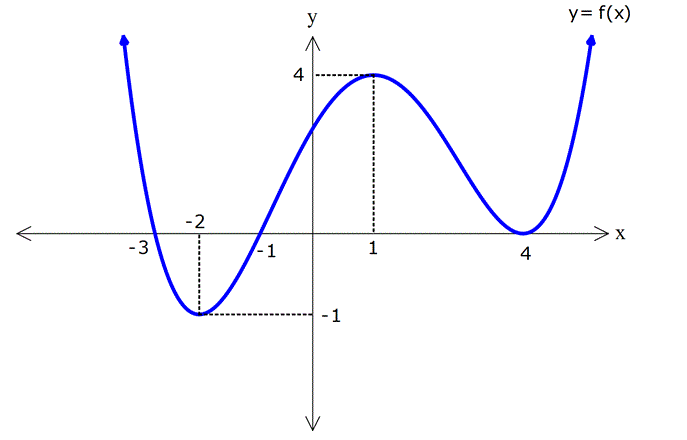
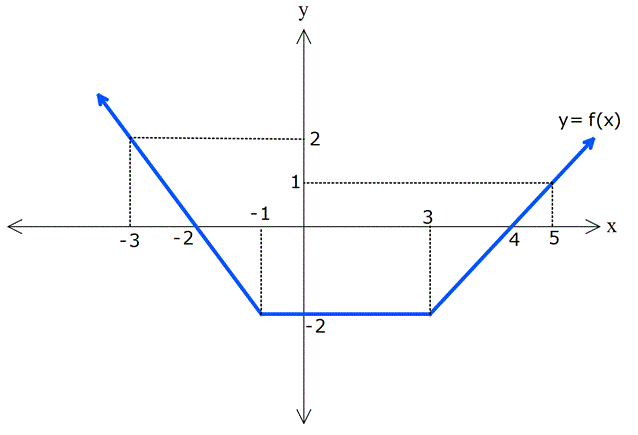
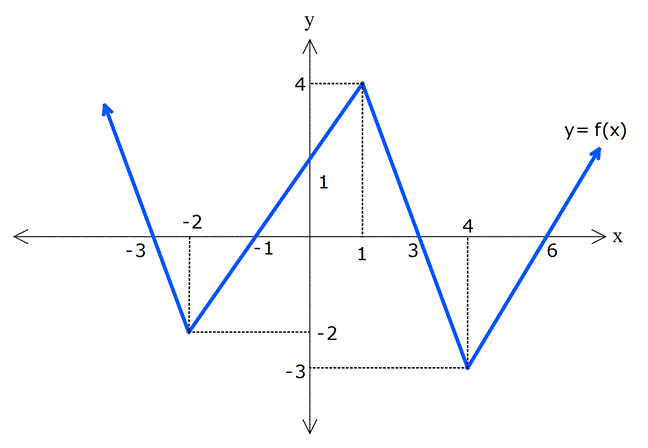
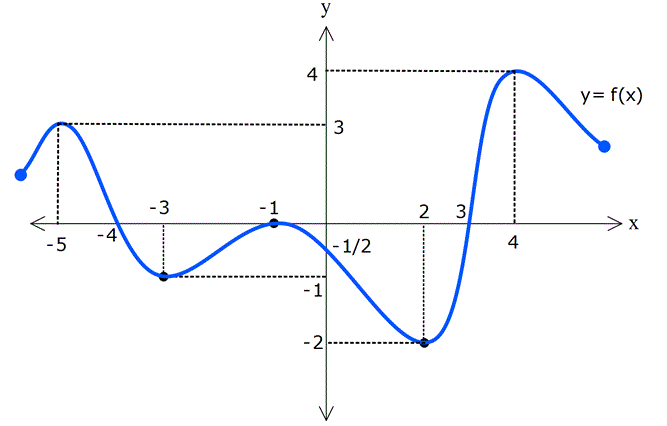
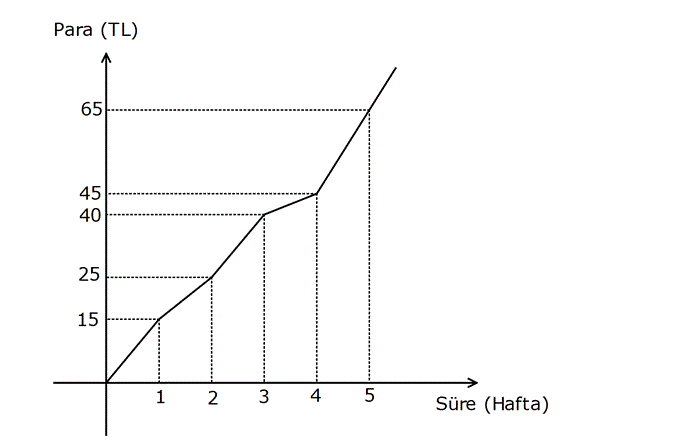
FONKSİYON UYGULAMALARI TESTİ www.matematikkolay.net 1) Yukarıdaki şekilde y f(x) fonksiyonunun grafiği verilmiştir. Buna göre, grafiğin eksenleri kestiği noktaların koordinatları toplamı kaçtır? A) 6 B) 4 C) 2 D) 0 E) 2 ÇÖZÜM: Grafik x eksenini ( 4,0) , ( 1, 0) ve (2, 0) noktala – rında kesiyor. y eksenini ise, (0, 1) noktasında kesiyor. Bunları toplarsak, 4 ( 1) 2 ( 1) 4 buluruz. Cevap: B 2) Yukarıdaki y f(x) fonksiyonunun grafiği verilmiştir. Buna göre, y f(x) fonksiyonunun negatif değerler aldığı en geniş aralık hangi şıkta doğru gösterilmiştir? A) ( , 3) ( 1, 2) B) ( 4, 3) C) ( 1, 2) (3, ) D) ( 4, 1) ( 1, 3) E) ( 4, 3) 2 ÇÖZÜM: Grafiğk, x ekseninin altında ise fonksiyon negatif değerler alır. Bu sebeple x 4′ ten 1’e kadar ve 1 den 3’e kadar olan bölgede f(x) negatiftir. Aralık olarak yazarsak, ( 4, 1) ( 1, 3) şeklinde ifade edebiliriz. Cevap:D 3) Yukarıdaki şekilde y f(x) fonksiyonunun grafiği verilmiştir. Buna göre, f(x)’in artan olduğu en geniş aralık aşağıdakilerden hangisidir? A) [ 2, 1] [4, ) B) [ 2, 1] [4, ) C) [ 2, 4] D) [ 3, 2] [1, ) E) [4, ) ÇÖZÜM: Grafiğe göre, x 2 den 1’e kadar fonksiyon artmak – tadır. Ayrıca x 4 ten sonra devamlı artmaktadır. O halde, ar tan aralıkları [ 2, 1] [4, ) şeklinde ifade edebiliriz. Not : Ar tan, azalan aralıklara uç nok talar da dahil edilir. Cevap: A www.matematikkolay.net 4) Yukarıdaki şekilde y f(x) fonksiyonunun grafiği verilmiştir. Buna göre, f fonksiyonu ile ilgili aşağıdakilerden hangisi doğrudur? A) (5, 6) aralığında negatif değerli ve azalandır. B) (3, 4) aralığında p ozitif değerli ve ar tandır. C) ( 1, 3) aralığında negatif değerli ve ar tandır. D) ( 2, 1) aralığında negatif değerli ve azalandır. E) ( 4, 3) aralığında pozitif değerli ve ar tandır. ÇÖZÜM: Şıklara tek tek bakalım. A) (5, 6) aralığında grafik, x ekseninin üstündedir, pozitiftir. A yanlış. B) (3, 4) aralığında grafik, x ekseninin altındadır. negatiftir. B yanlış. C) (1, 3) aralığında grafik, x ekseninin altındadır. negatiftir. Doğru. Ancak, f(x) burada sabittir. C yanlış. D) ( 2, 1) aralığında grafik, x ekseninin altındadır. negatiftir. Doğru. Ayrıca, grafi k sürekli olarak azalmaktadır. D şıkkı doğru. E) ( 4, 3) aralığında grafik, x ekseninin üstündedir, pozitiftir. Doğru. Ancak, grafik sürekli azalmaktadır. Ar tan olamaz. E yanlış. Ceva p: D 5) Yukarıdaki şekilde y f(x) fonksiyonunun grafiği verilmiştir. Buna göre, f fonksiyonunun ( 3, 6) aralığındaki maksimum değeri ile minimum değerinin çarpımı kaçtır? A) 24 B) 20 C) 18 D) 15 E) 12 ÇÖZÜM: ( 3, 6) aralığında f(x) en büyük değerini (1, 4) nok – tasında almıştır ve en büyük değeri 4 tür. En küçük değerini ise (4, 3) noktasında almıştır. En küçük değeri de 3 tür. Bu değerleri çarparsak, 4.( 3) 12 buluruz. Cevap:E 6) Yukarıdaki şekilde y f(x) fonksiyonunun grafiği verilmiştir. Buna göre, aşağıdaki ifadelerden hangisi yanlıştır? A) Fonksiyon ( 3, 1) aralığında negatif değerli artandır. www.matematikkolay.net B) Fonksiyon ( 1, 2) aralığında negatif değerli artandır. C) Grafiğin eksenleri kestiği noktaların koordinatları 5 toplamı dir. 2 D) Fonksiyonun ( 5, 4) aralığındaki maksimum değeri ile mi nimum değerinin farkının mutlak değeri 6 dır. E) Fonksiyon [2, 4] aralığında artandır. ÇÖZÜM: Şıklara tek tek bakalım. A) x 3 ile x 1 arasında fonksiyon, x ekseninin altındadır. Dolayısıyla negatiftir. Ayrıca bu aralıkta fonksiyon artmaktadır. A şıkkı doğru B) x 1 ile x 2 arasında fonks iyon, x ekseninin altındadır. Dolayısıyla negatiftir. Doğru. Ancak fonksiyon azalmaktadır. B şıkkı yanlış. C) Grafiğin eksenleri kestiği noktaların koordinatları 1 toplarsak 4 ( 1) 3 2 5 buluruz. 2 D) ( 5, 4) aralığında maksimum değeri 4, minimum değeri 2 dir. Farkı 4 ( 2) 6 dır, doğru. E) x 2 den 4’e doğru fonksiyon artmaktadır. E şıkkı doğru. Cevap : B 7) f(x) ax 3 fonksiyonunun değişim hızı 1 olduğuna göre, f(2) kaçtır? A) 1 B) 0 C) 1 D) 2 E) 3 ÇÖZÜM: Doğrusal fonksiyonun eğimi, aynı zamanda değişim hızıdır. Bu nedenle, f(x) x 3 tür. f(2) 23 1 dir. Cevap: C 8) f(x) (a 3)x 5 fonksiyonunun değişim hızı pozitif olduğuna göre, a’nın değer aralığı aşağıdakilerden hangisidir? A) (-3, 5) B) (-3, ) C) (3, 5) D) (5, ) E) (-3, 5) ÇÖZÜM: Değişim hızı pozitif ise, doğrusal fonksiyonun eğimi de pozitiftir. Bu nedenle, a 3 0 a 3 tür. a ( 3, ) dur. Cevap: B 9) Yukarıdaki grafik, Mert’in kumbarasında biriken parayı göstermektedir. 1 ile 4. haftalar arasında bu paranın ortalama değişim hızı kaçtır? A) 5 B) 6 C) 8 D) 10 E) 11 ÇÖZÜM: f(4) f(1) 45 15 30 Ort. Değişim Hızı 10 dur. 4 1 3 3 Cevap: D 10) 2 f(x) 2x 5x 10 fonksiyonunun [2, 4] aralığındaki ortalama değişim hızı kaçtır? A) 7 B) 5 C) 4 D) 2 E) 2 ÇÖZÜM: f(4) f(2) Ort. Değişim Hızı 4 2 32 20 10 8 10 10 2 2 12 14 7 dir. Cevap: A 2 2


8.sorunun cevabı doğru mu? bir önceki soru ile mukayese edince (a+3)x-5>0 olmalı. Bu durumda sonuç da değişir.
Tekrar kontrol ettik, çözümde bir hata göremedik.
Değişim hızı x’in katsayısı ile ilgili bir durum. O yüzden, x’in katsayısı 0 dan büyük olacak şekilde çözüme başlamalıyız.