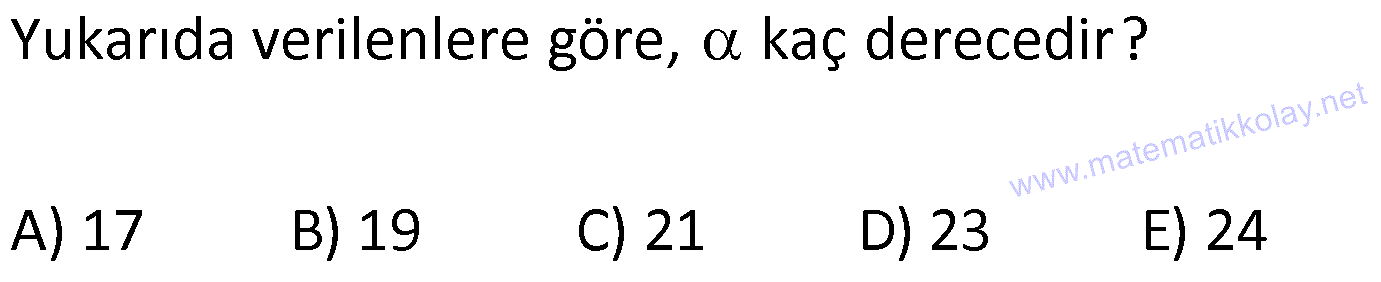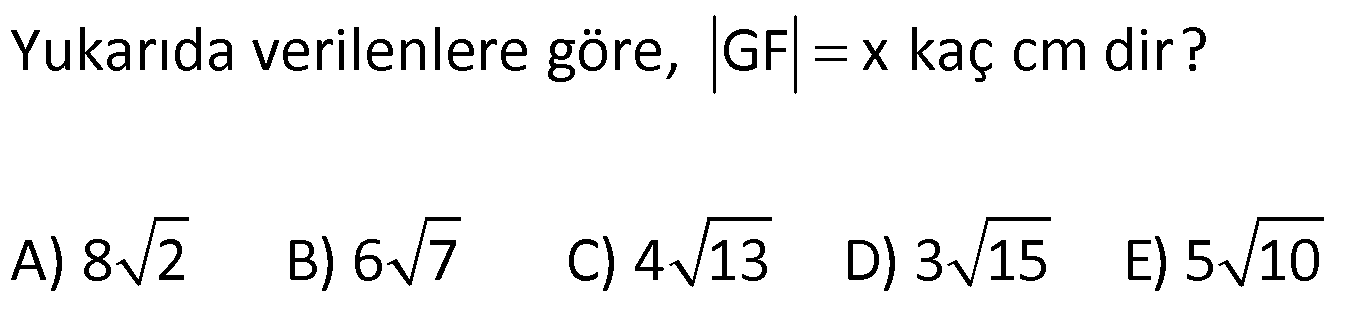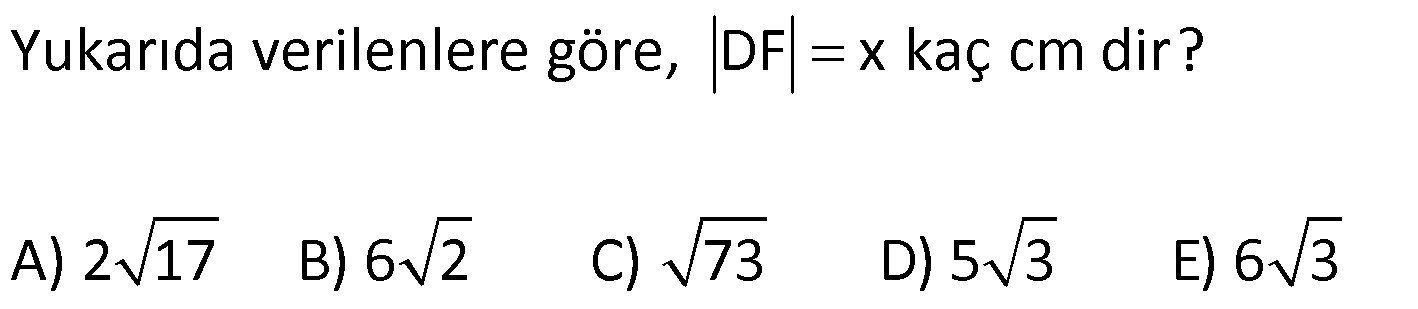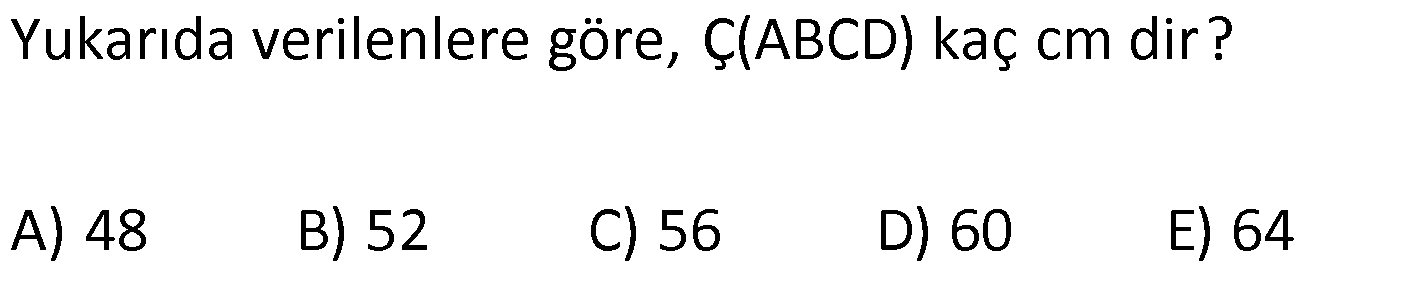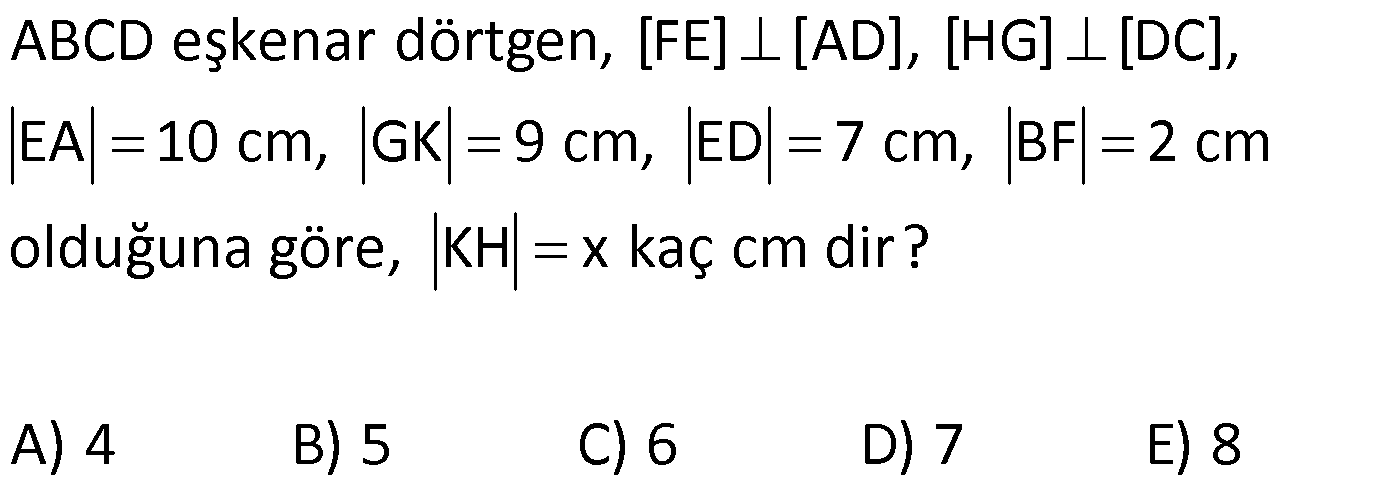Bu bölümde Eşkenar Dörtgen ile ilgili 20 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
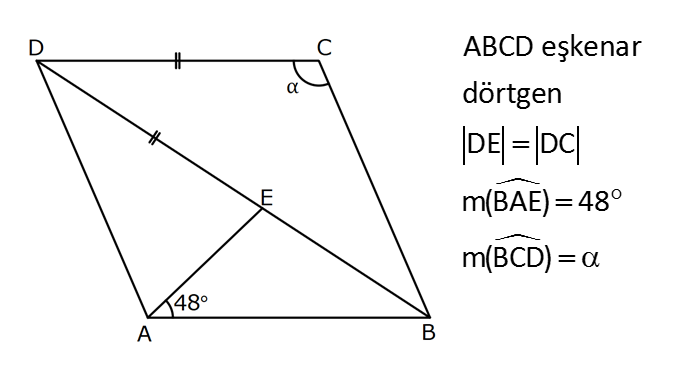
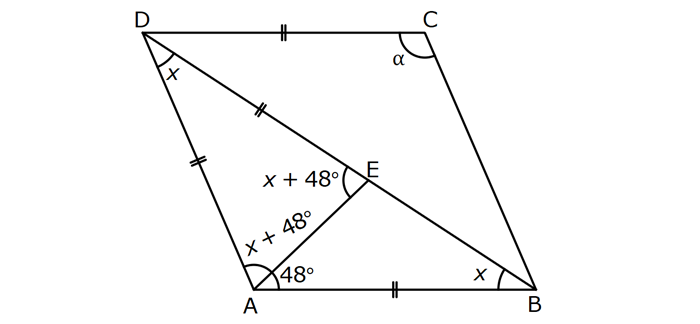
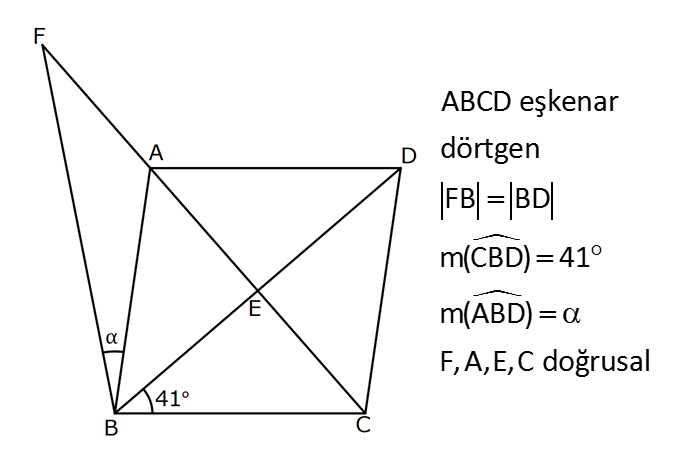
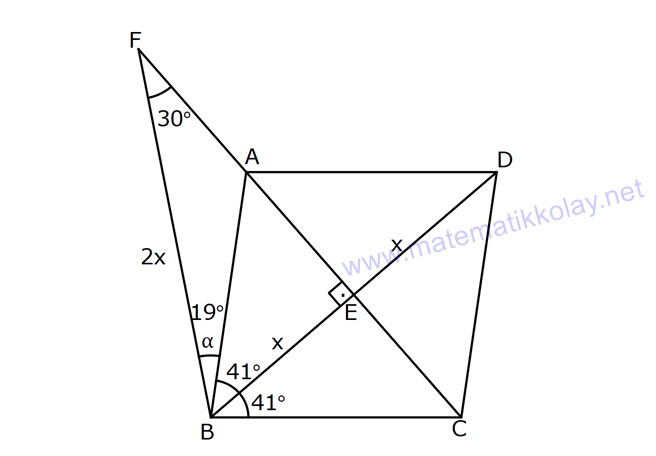
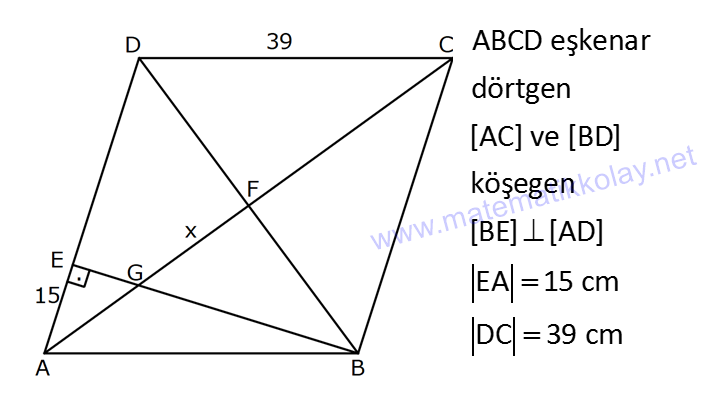
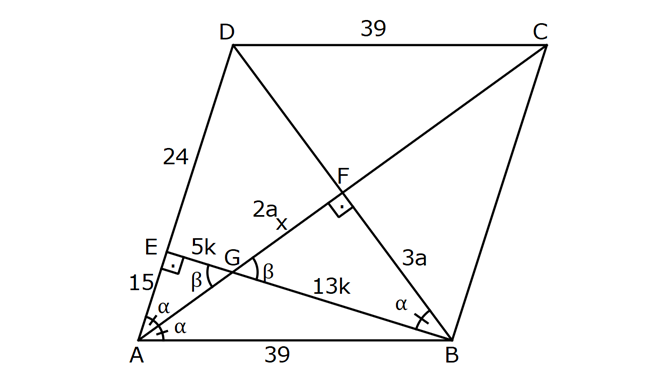
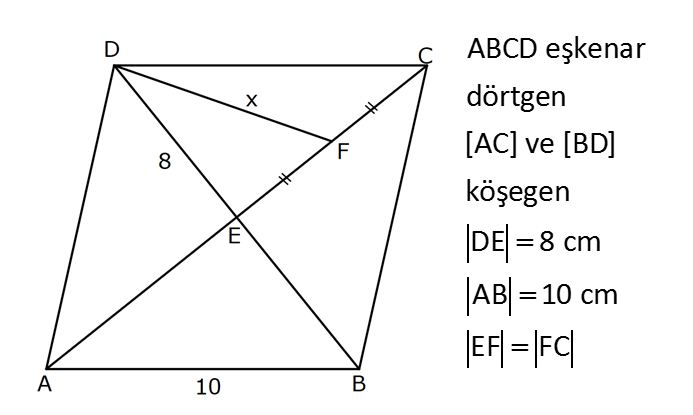
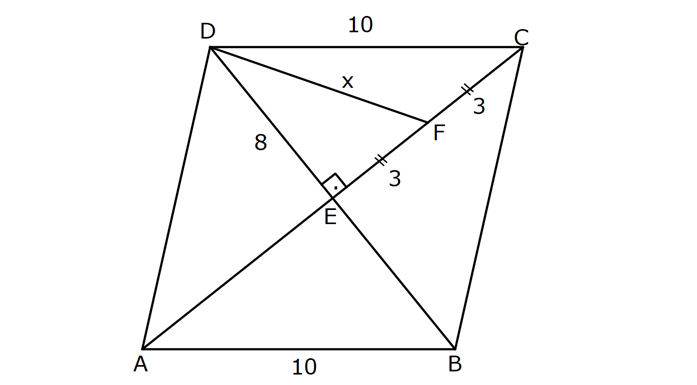
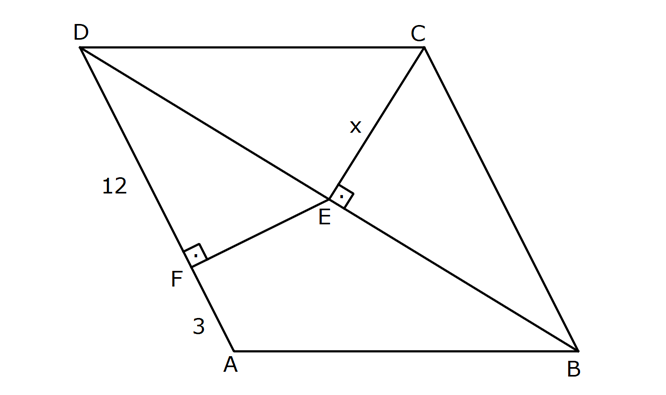
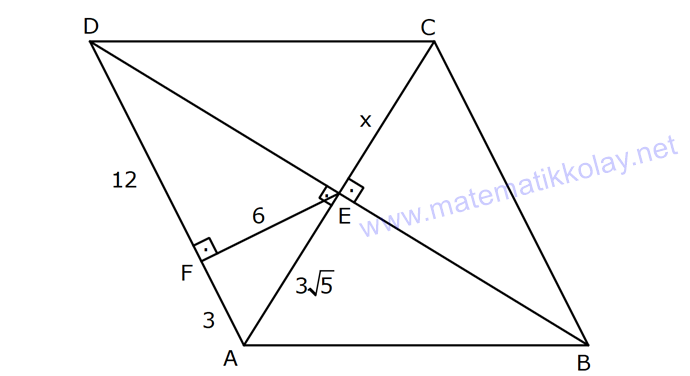
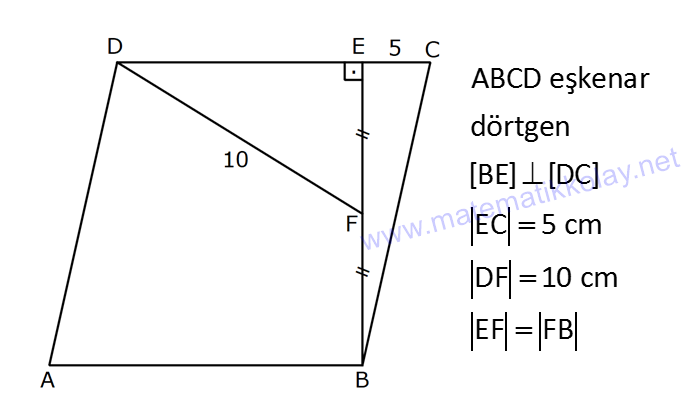
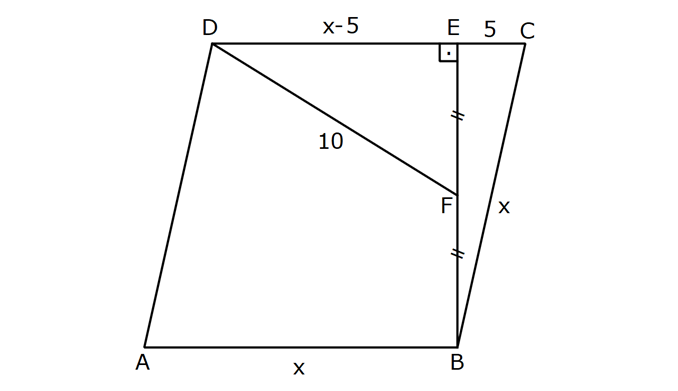
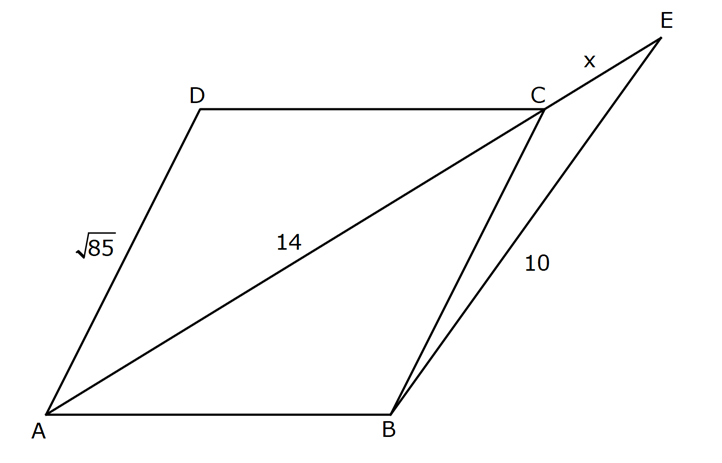
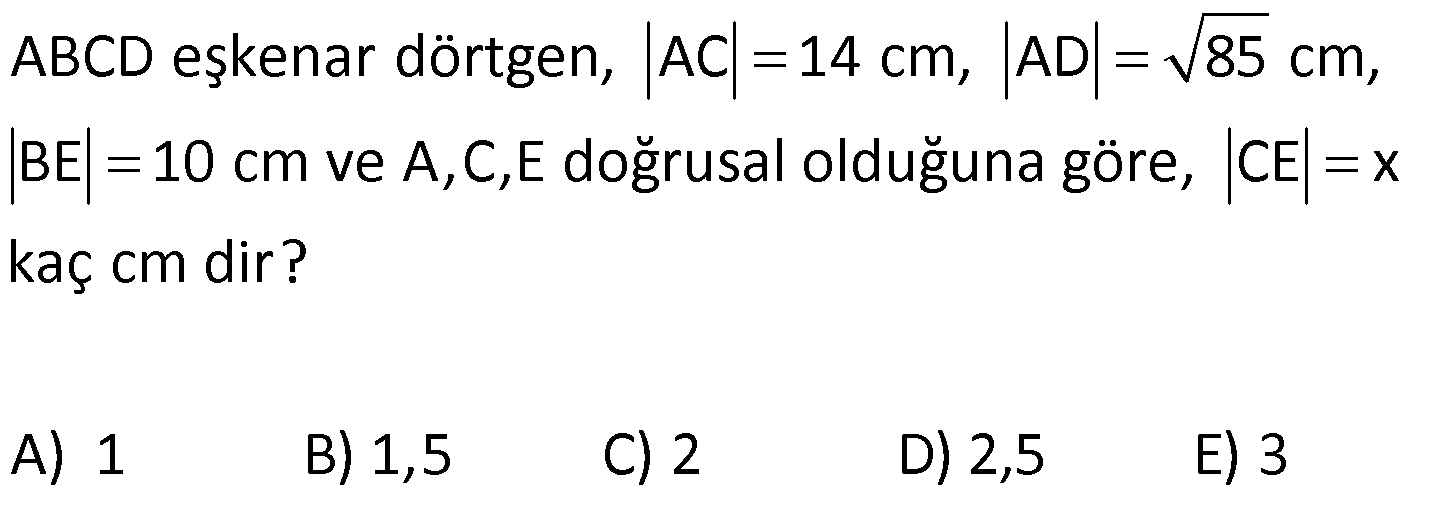
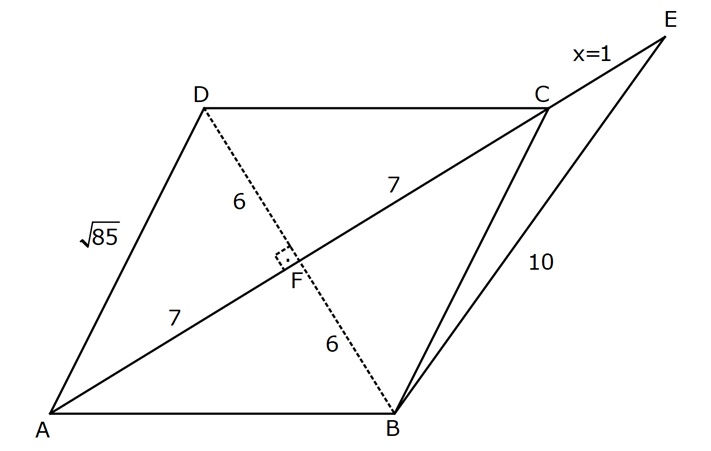
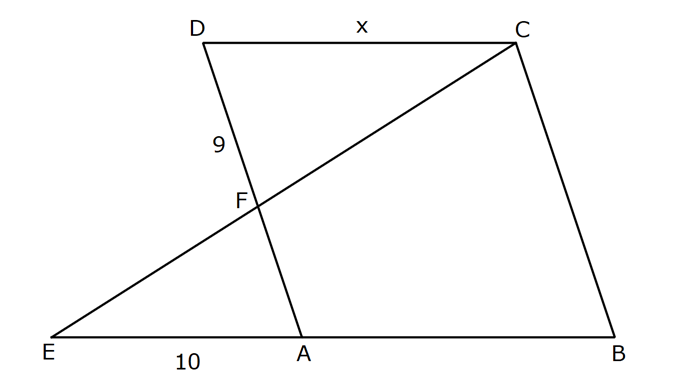
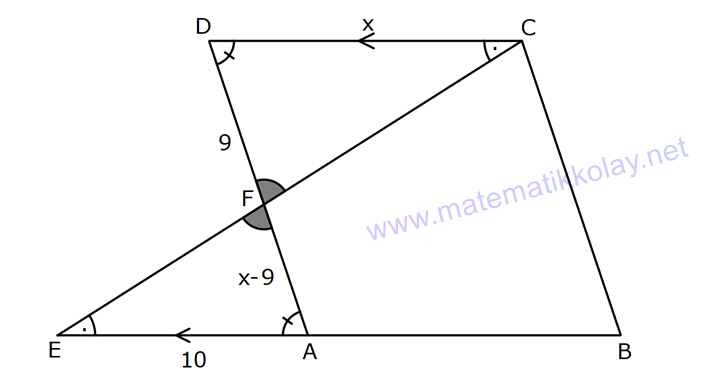
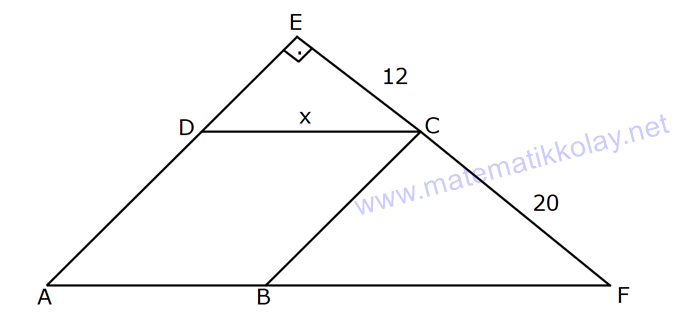
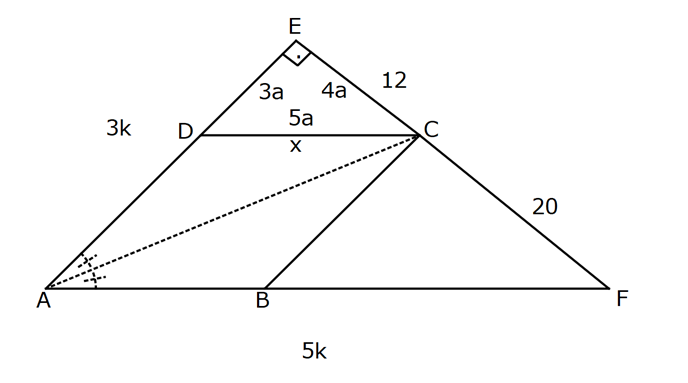
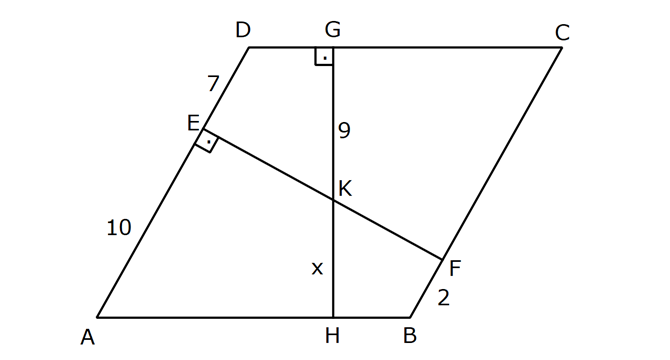
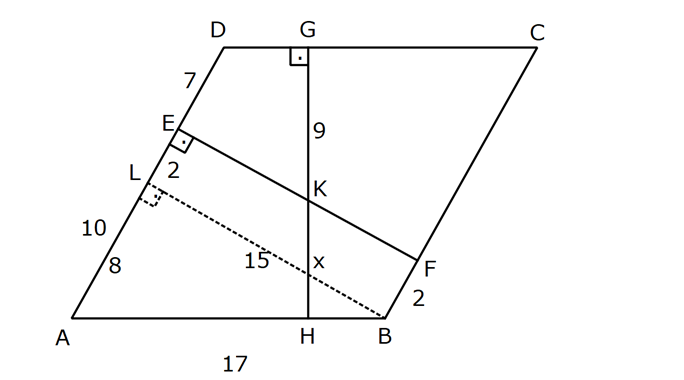
EŞKENAR DÖRTGEN www.matematikkolay.net 1) ABCD eşkenar dörtgen DE DC m(BAE) 48 m(BCD) Yukarıda verilenlere göre, kaç derecedir ? A) 96 B) 104 C) 114 D) 120 E) 124 ÇÖZÜM: m(ABD) x diyelim. Eşkenar dörtgenin tüm kenarları birbirine eşittir. Buna göre, AB AD olduğu için BAD üçgeni ikizkenar bir üçgendir ve m(ADB) x olur. m(AED) m(EBA) m((EAB) x 48 olur. AD DE olduğu için Not : 28 de ADE üçgeni ikizkenardır. Dolayısıyla m(DAE) x 48 olur. ADE üçgeninin iç açıları toplamından x (x 48 ) (x 48 ) 180 3x 96 180 3x 84 x 28 dir. m(BAD) x 48 48 124 olur. Eşkenar dörtgen, parale Not : lkenara ait tüm özellikleri taşır. Karşılıklı açılar birbirine eşit olacağı için, 124 buluruz. Cevap : E 2) ABCD eşkenar dörtgen FB BD m(CBD) 41 m(ABD) F,A,E,C doğrusal Yukarıda verilenlere göre, kaç derecedir ? A) 17 B) 19 C) 21 D) 23 E) 24 ÇÖZÜM: www.matematikkolay.net Eşkenar dörtgende köşegenler birbirini dik ortalar. Buna göre, m(BEF) 90 dir. BD 2x dersek, BE ED x olur. FB BD verildiği için de FB 2x tir. O halde, FBE üçgeni bir 30 – 60 – 90 üçgenidir. m(FBE) 60 dir. Not : Eşkenar dörtgende köşegenler aynı zamanda açıortaydır. Bu sebeple m(ABE) 41 dir. O halde, 60 41 19 dir. Cevap : B Not : 3) ABCD eşkenar dörtgen [AC] ve [BD] köşegen [BE] [AD] EA 15 cm DC 39 cm Yukarıda verilenlere göre, GF x kaç cm dir ? A) 8 2 B) 6 7 C) 4 13 D) 3 15 E) 5 10 ÇÖZÜM: [AC] açıortaydır. Buna göre, EF 15 5 FB 39 13 15 39 36 EF 5k, FB 13k diyebiliriz. Ayrıca EAB üçgeni, 5 -12 -13 üçgeninin katlarıyla oluşturulmuştur. Bu sebeple EB 36 dır. 18k 36 k 2 dir. EG 5.2 10 cm olur, GB 13.2 26 cm olur. Eşkenar dörtgende köşegenler dik kesiştiği için, m(BFG) 90 dir. Açıların aynı olmasından dolayı AEG üçgeni ile BFG üçgeni benzerdir. FB 15 3 x 10 2 2 2 2 2 2 2 FB 3a , x 2a diyebiliriz. BFG üçgeninde pisagordan (2a) (3a) 26 4a 9a 26 13 2 a 26 2 2 .26 a 52 a 2 13 cm dir. O halde, x 2a 4 13 cm buluruz. Cevap : C www.matematikkolay.net 4) ABCD eşkenar dörtgen [AC] ve [BD] köşegen DE 8 cm AB 10 cm EF FC Yukarıda verilenlere göre, DF x kaç cm dir ? A) 2 17 B) 6 2 C) 73 D) 5 3 E) 6 3 ÇÖZÜM: 2 2 2 2 2 DC 10 cm dir. Eşkenar dörtgende köşegenler dik kesiştiği için, m(DEC) 90 dir. O halde, DEC üçgeni bir 6 – 8 -10 üçgenidir. EF 3 cm olur. DEF üçgeninde pisagordan x 8 3 x 64 9 x 73 x 73 cm dir. C evap: C 5) ABCD eşkenar dörtgen, [BD] köşegen, DF 12 cm, FA 3 cm, [CE] [BD] olduğuna göre, CE x kaç cm dir? A) 3 5 B) 4 C) 2 6 D) 5 E) 34 ÇÖZÜM: 2 2 2 2 2 2 [CE] yi uzatırsak [AC] köşegeni olur. Çünkü eşkenar dörtgende köşegenler dik kesişirdi. DEA üçgeninde öklit yaparsak, EF 3.12 EF 6 cm olur. EFA üçgeninde pisagor yaparsak, EA 3 6 EA 9 36 EA 45 E A 3 5 cm olur. Köşegenler birbirini ortaladığı için x 3 5 cm dir. Cevap : A 6) www.matematikkolay.net ABCD eşkenar dörtgen [BE] [DC] EC 5 cm DF 10 cm EF FB Yukarıda verilenlere göre, Ç(ABCD) kaç cm dir? A) 48 B) 52 C) 56 D) 60 E) 64 ÇÖZÜM: 2 2 2 2 2 2 2 Eşkenar dörtgenin bir kenarına x diyelim. DE x 5 cm olur. DEF üçgeninde pisagordan, EF 100 (x 5) EF 100 (x 5) dir. BEC üçgeninde pisagordan, EB x 25 EB x 25 tir. EB 2 EF olduğundan, x 25 2 2 2 2 2 2 2 2 2 2 2 2 2 2 13.May x 13 100 (x 5) kare alalım. x 25 4(100 (x 5) ) x 25 4(100 (x 10x 25)) x 25 4(100 x 10x 25) x 25 4(75 x 10x) x 25 300 4x 40x 5x 40x 325 0 5’e bölelim. x 8x 65 0 (x 13)(x 5) 0 x 13 cm dir. Ç(ABCD) 4.13 52 cm buluruz. Cevap : B 7) ABCD eşkenar dörtgen, AC 14 cm, AD 85 cm, BE 10 cm ve A,C,E doğrusal olduğuna göre, CE x kaç cm dir? A) 1 B) 1,5 C) 2 D) 2,5 E) 3 www.matematikkolay.net ÇÖZÜM: 2 2 2 [BD] köşegenini çizelim. Köşegenler birbirini dik ortalayacağı için, AF FC 7 cm olur. ADF üçgeninde pisagordan, DF 85 7 DF 36 DF 6 cm olur. FB 6 cm dir. O halde, FEB üçgeni bir 6 – 8 -10 üçgenid ir. FE 8 cm olur. x 8 7 1 cm buluruz. Cevap : A 8) ABCD eşkenar dörtgen, EA 10 cm, DF 9 cm, E,A,B doğrusal ve E,F,C doğrusal olduğuna göre, DC x kaç cm dir? A) 12 B) 13 C) 15 D) 16 E) 18 ÇÖZÜM: 2 2 15.Haz x 15 Eşkenar dörtgenin bir kenarı x cm olduğundan, FA x 9 cm dir. [DC] // [EA] olduğundan, FDC üçgeni ile FAE üçgeni arasında kelebek benzerliği yapabiliriz. x 9 10 x 9 x 9x 90 x 9x 90 0 (x 15)(x 6 ) 0 x 15 cm buluruz. Cevap : C 9) ABCD eşkenar dörtgen, AEF üçgen, [AE] [EF], EC 12 cm, CF 20 cm olduğuna göre, DC x kaç cm dir? A) 15 B) 16 C) 18 D) 20 E) 21 ÇÖZÜM: www.matematikkolay.net Eşkenar dörtgenin köşegenleri açıortay olduğundan, [AC] açıortaydır. AE 12 3 AF 20 5 AE 3k ve AF 5k diyebiliriz. E açısı 90 olduğundan AEF üçgeni bir 3k – 4k – 5k üçgenidir. [DC] // [AF] olduğundan, DEC üçgeni de AEF üçgenine benzerdir. Yani DEC üçgeni de bir 3a- 4a- 5a üçgenidir. 4a 12 3 a 3 tür. x 5a 15 cm buluruz. Cevap : A 10) ABCD eşkenar dörtgen, [FE] [AD], [HG] [DC], EA 10 cm, GK 9 cm, ED 7 cm, BF 2 cm olduğuna göre, KH x kaç cm dir? A) 4 B) 5 C) 6 D) 7 E) 8 ÇÖZÜM: ALB dik üçgenini oluşturalım. AL 8 cm olur. AB 17 cm dir. O halde bu bir 8 -15-17 üçgenidir. LB 15 cm dir. Yani, eşkenar dörtgenin yüksekliği 15 cm dir. Eşkenar dörtgenin yüksekliği her yerde aynıdır. Not : Buna göre, x 15 9 6 cm dir. Cevap : C
