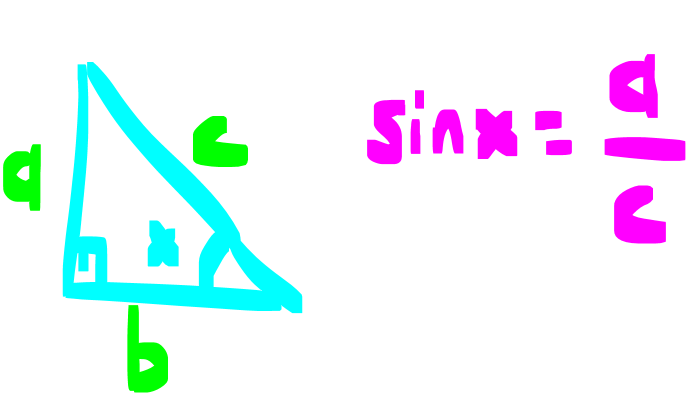 Bu bölümde Dik Üçgende Trigonometri ile ilgili 19 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Dik Üçgende Trigonometri ile ilgili 19 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
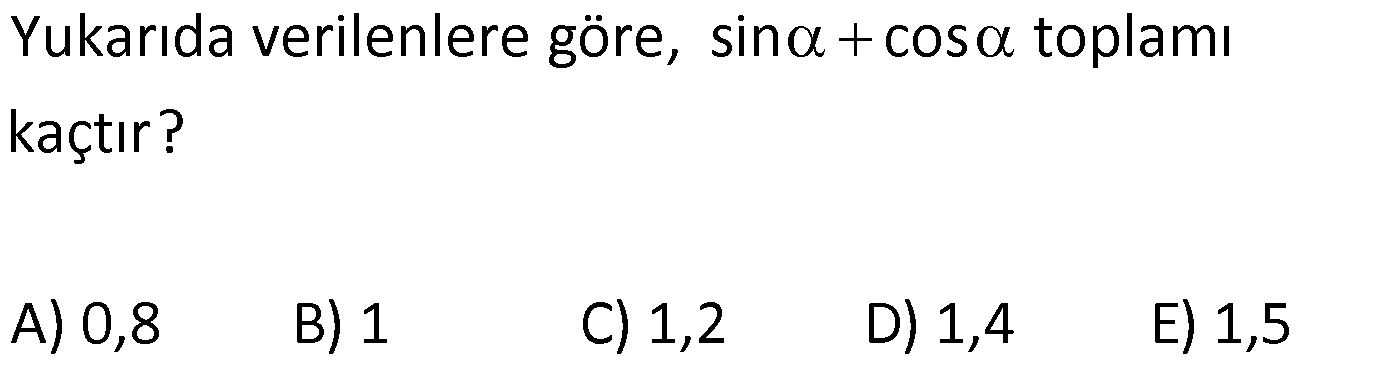
| | | | | |
Çözüm için Tıklayınız.

2.SORU
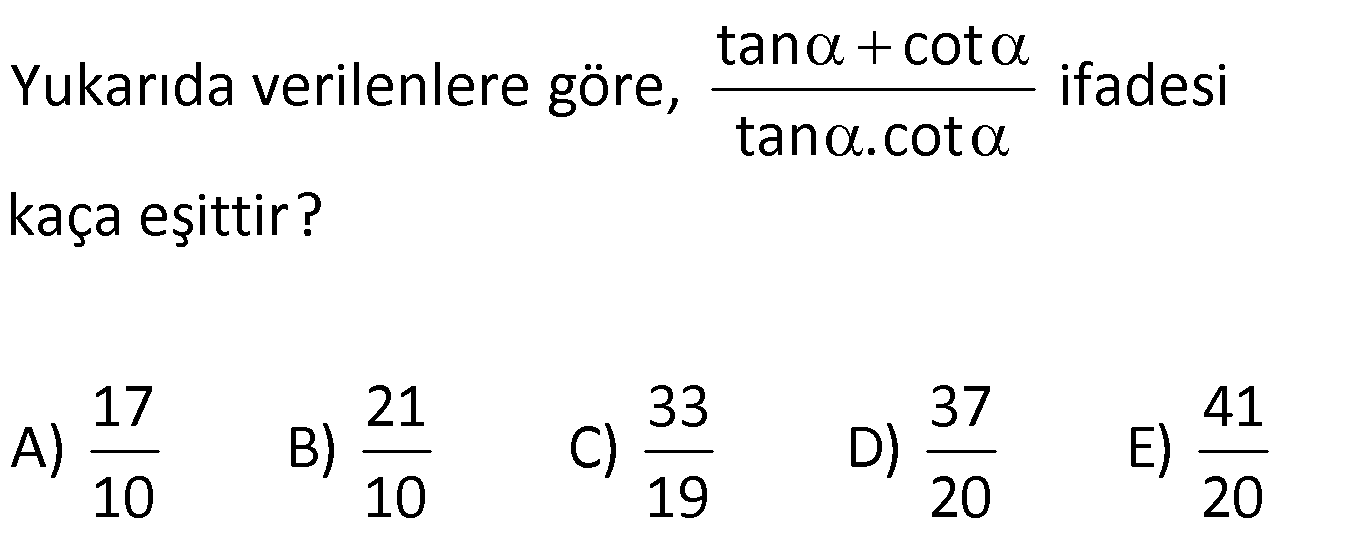
| | | | | |
Çözüm için Tıklayınız.

3.SORU
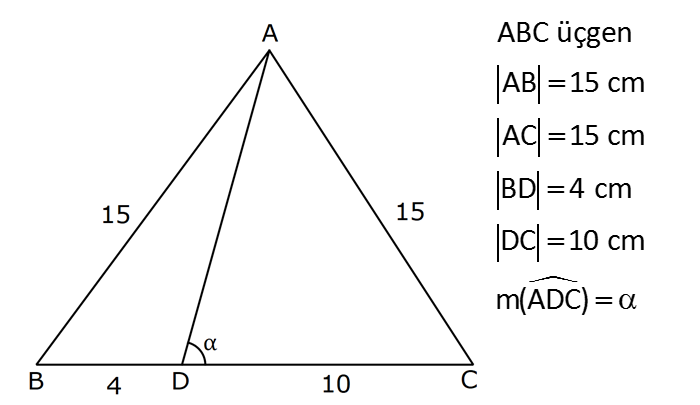
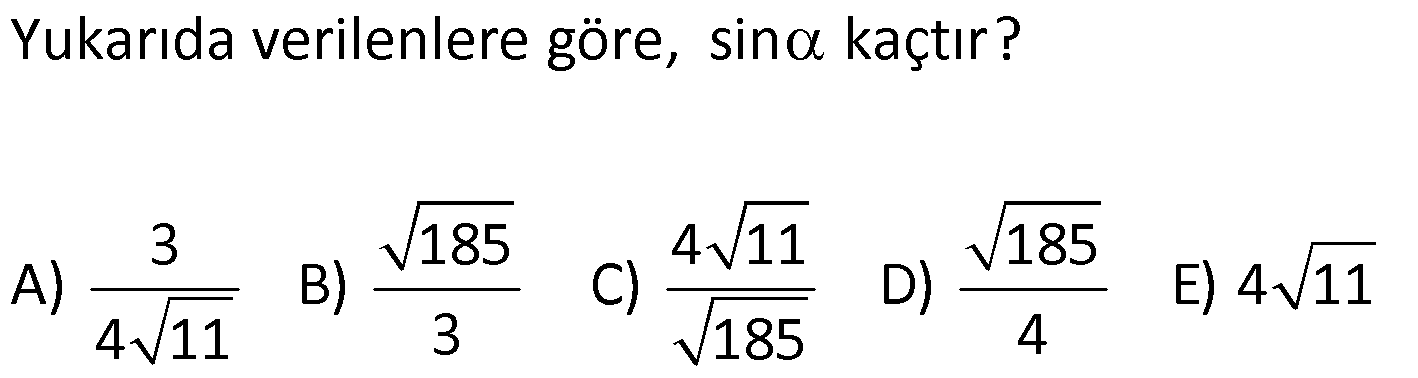
| | | | | |
Çözüm için Tıklayınız.
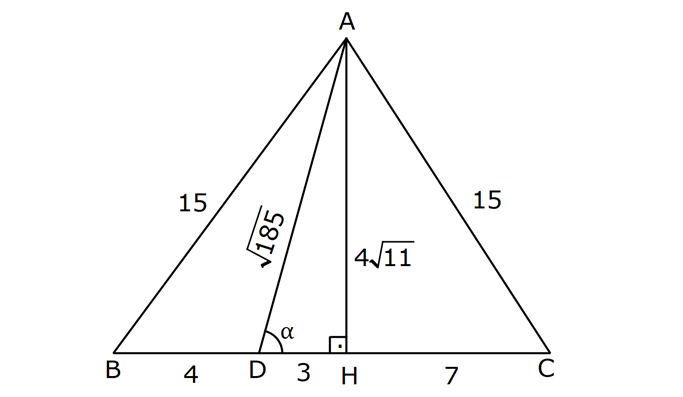

4.SORU

 | | | | |
Çözüm için Tıklayınız.

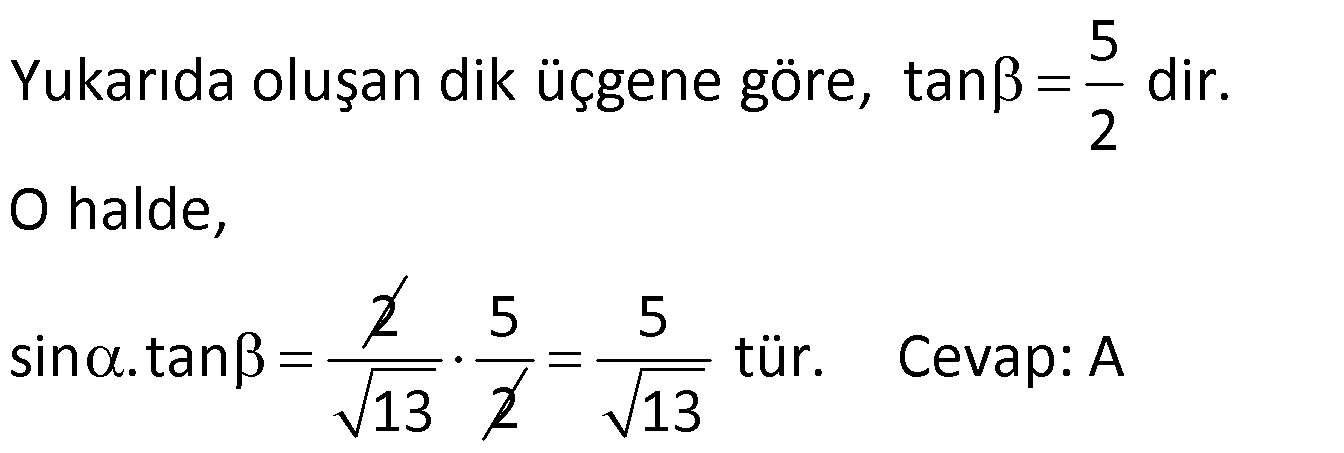
5.SORU
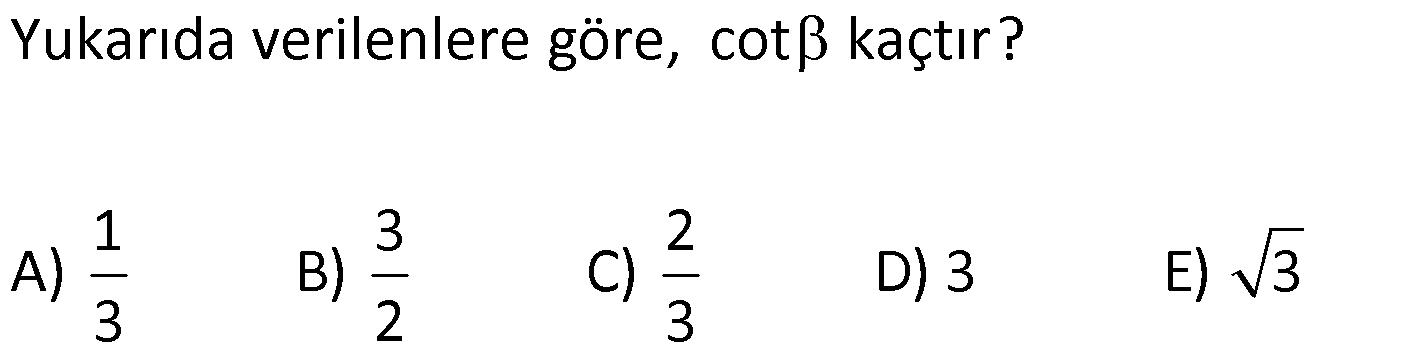
| | | | | |
Çözüm için Tıklayınız.

6.SORU
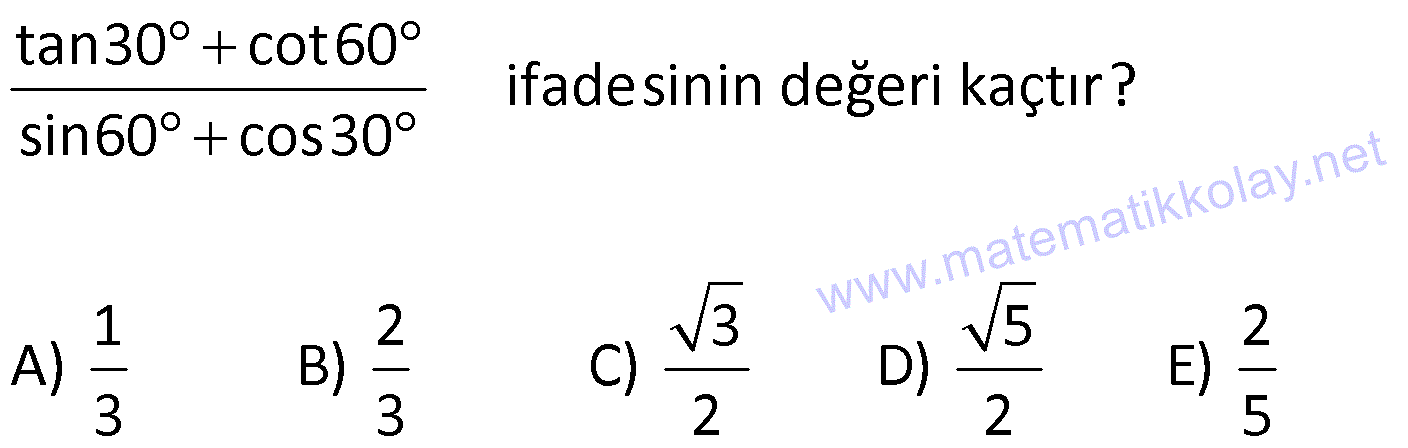
| | | | | |
Çözüm için Tıklayınız.
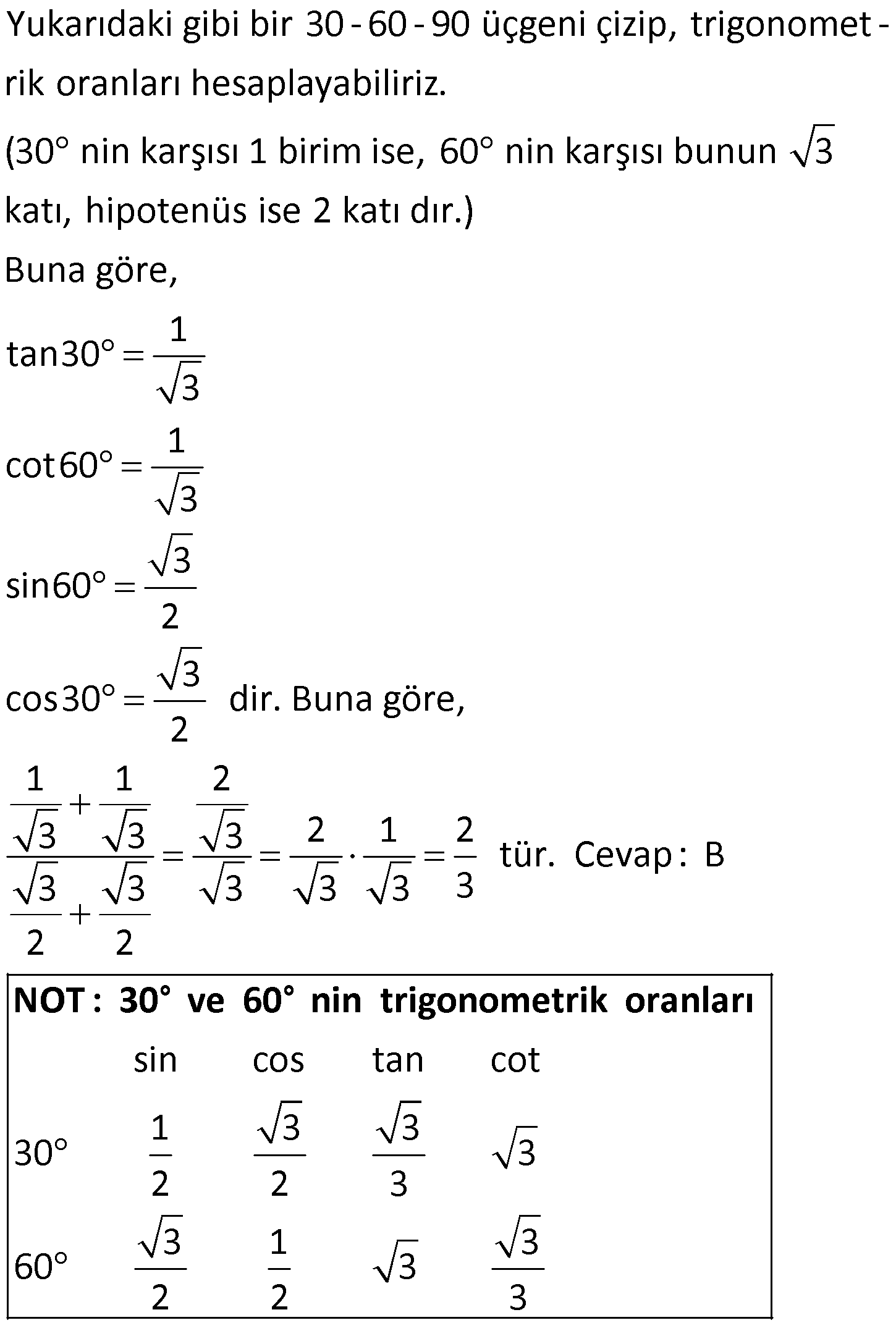
7.SORU
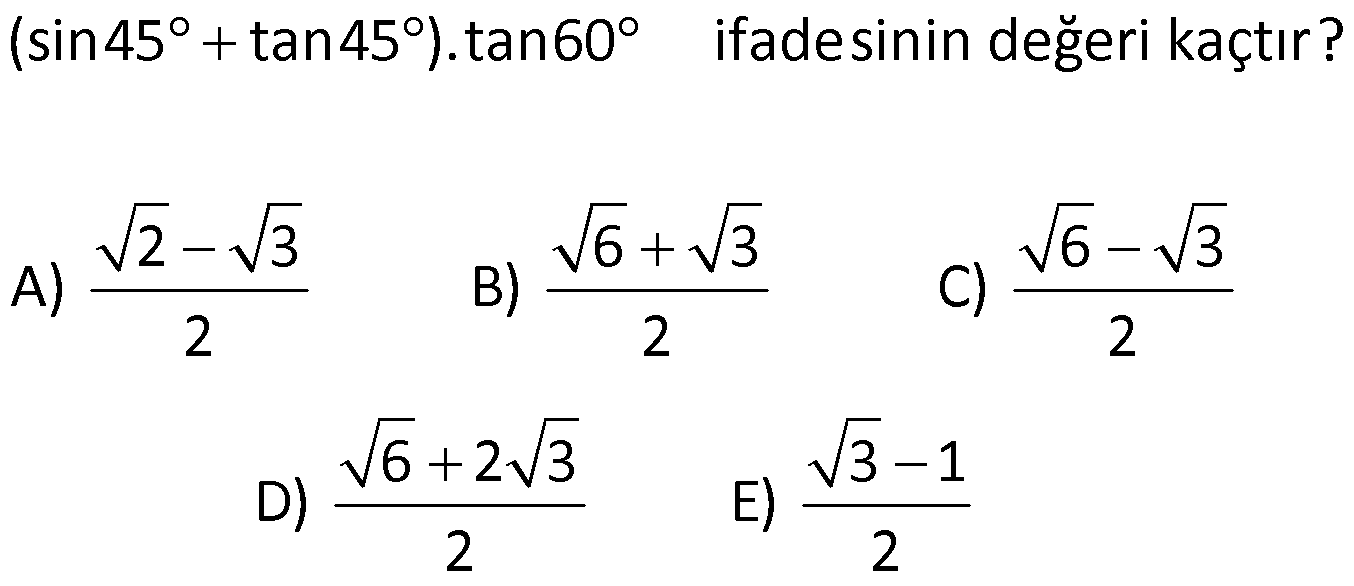
| | | | | |
Çözüm için Tıklayınız.

8.SORU

| | | | | |
Çözüm için Tıklayınız.
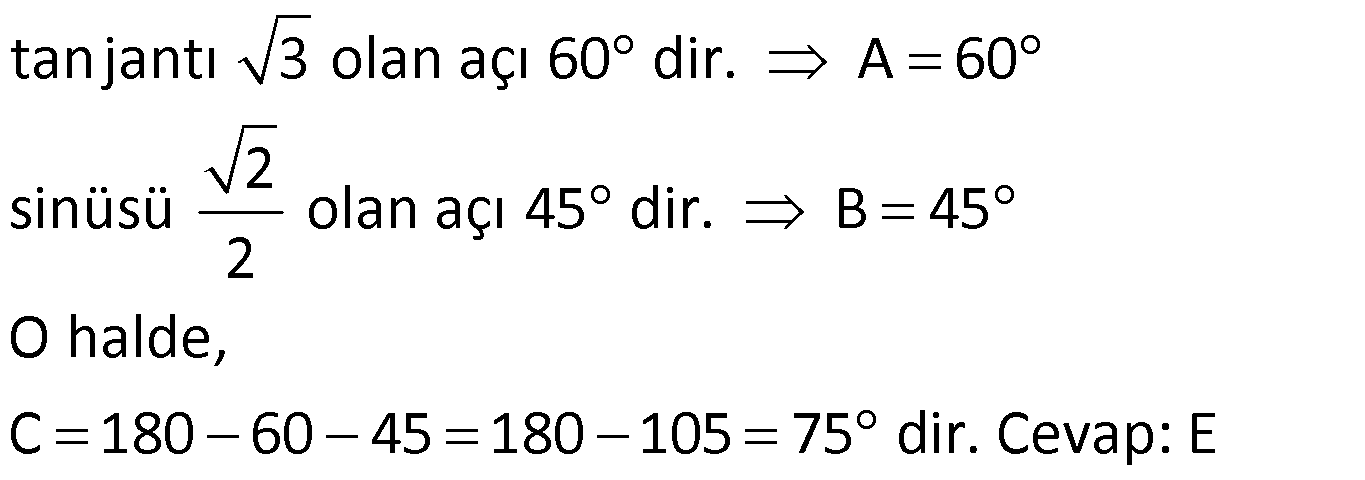
9.SORU
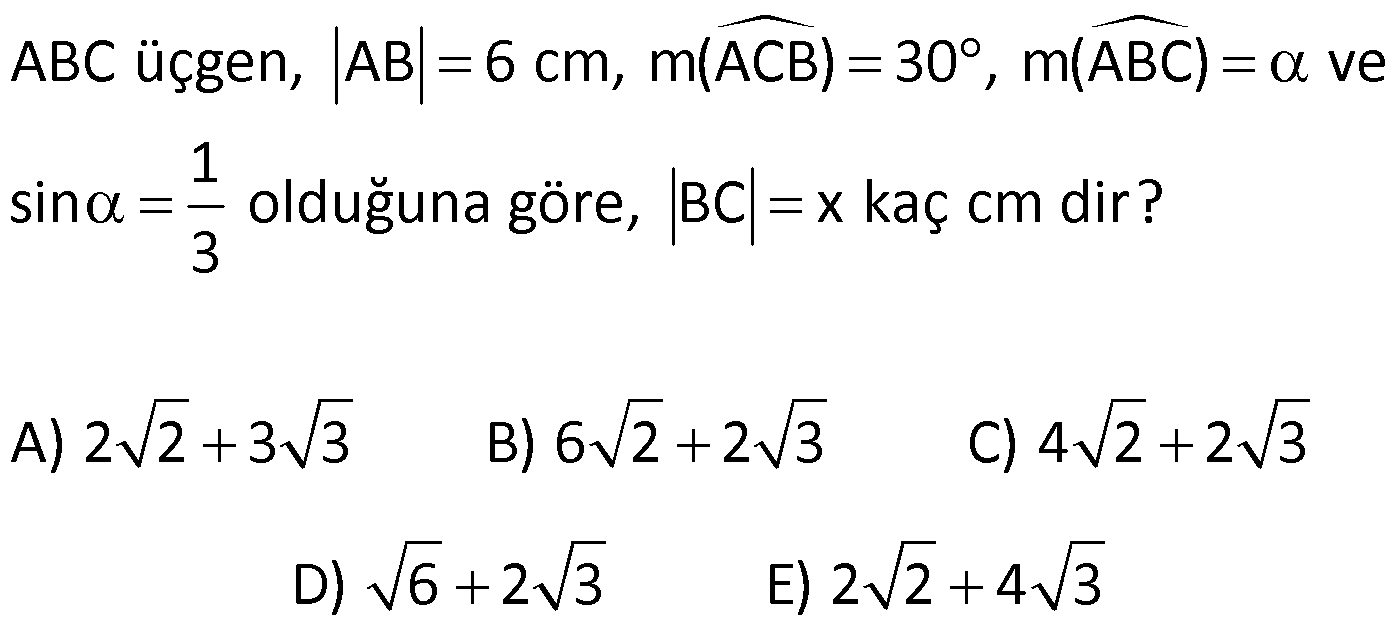
| | | | | |
Çözüm için Tıklayınız.

10.SORU
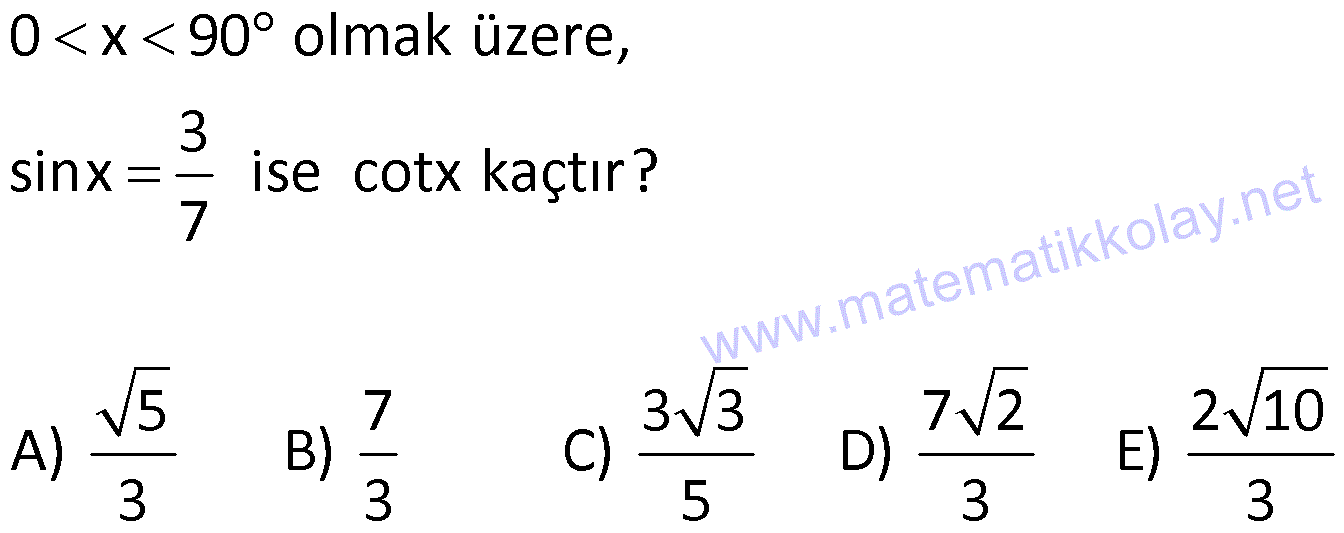
| | | | | |
Çözüm için Tıklayınız.
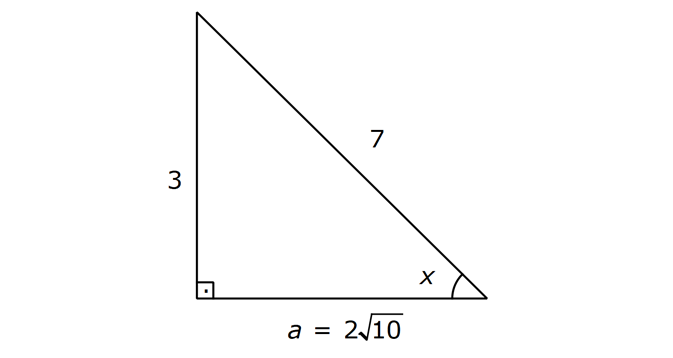

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
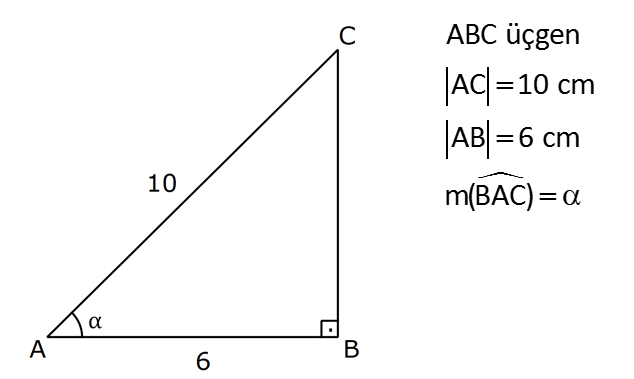
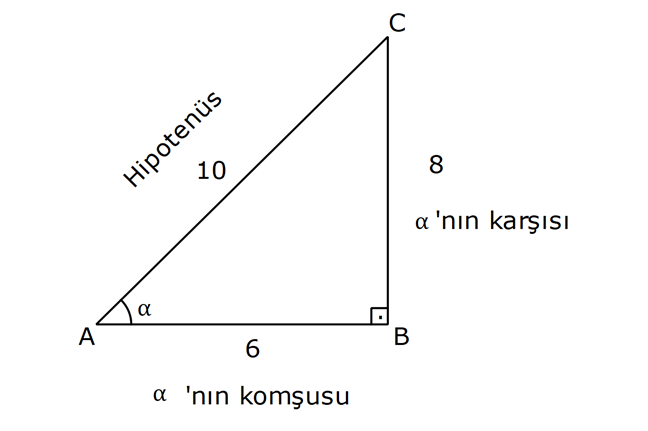
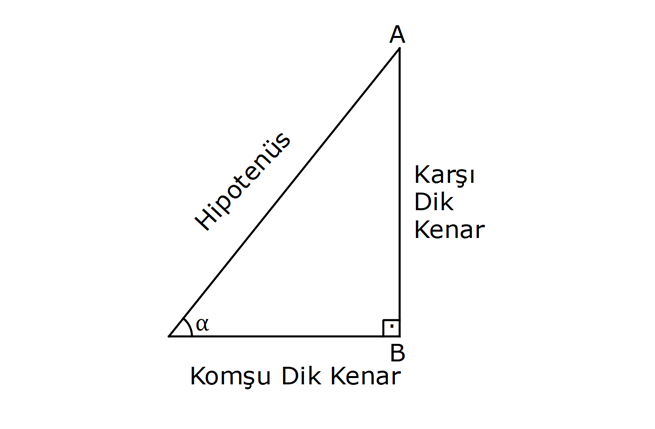
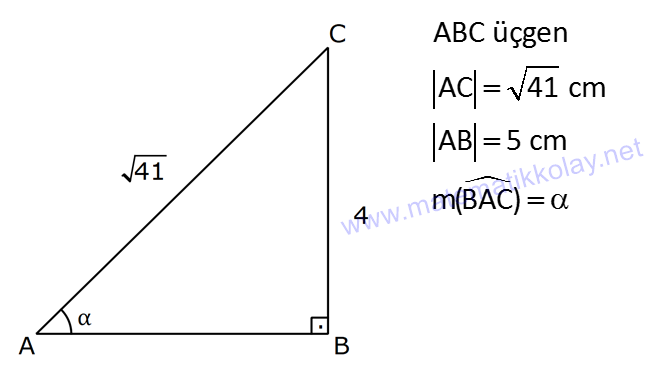
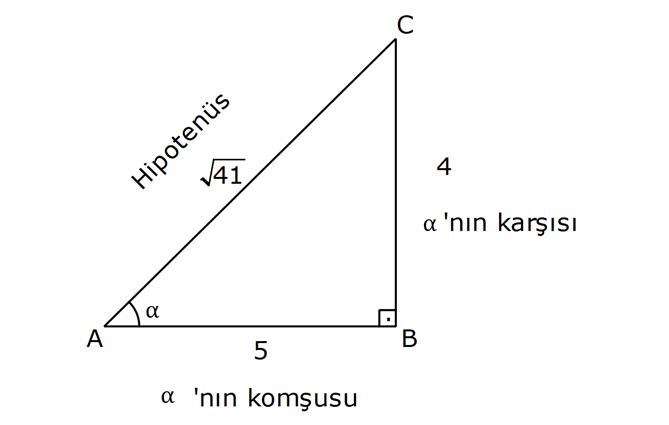
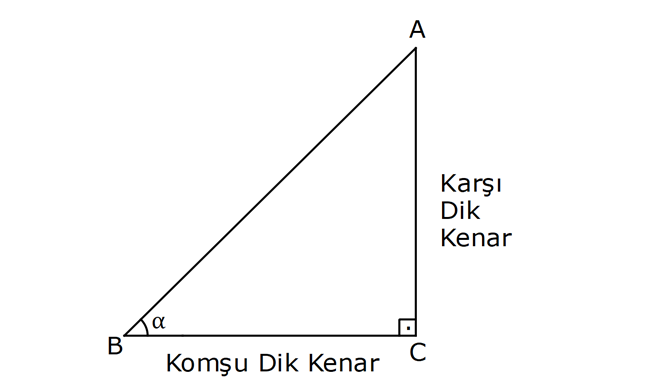
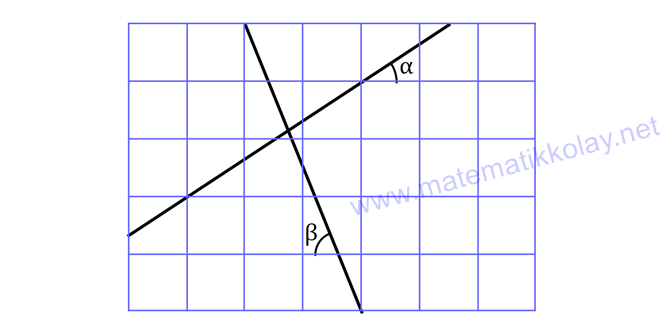
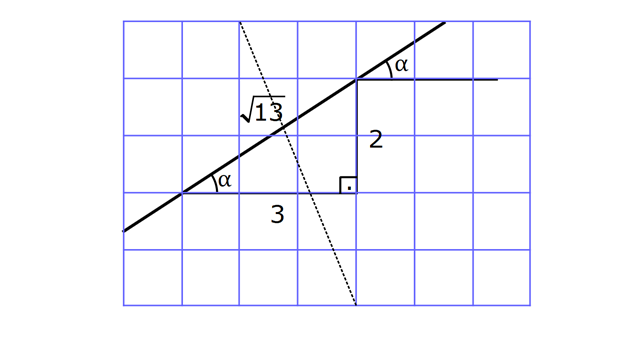
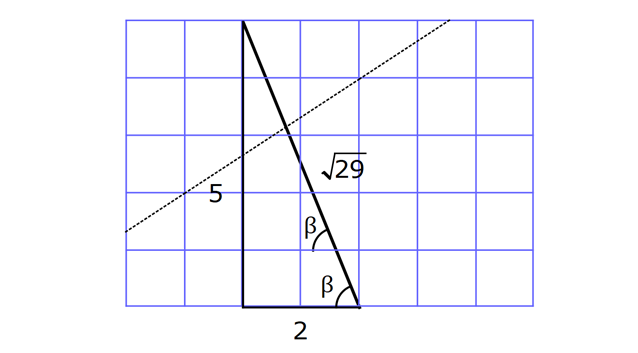
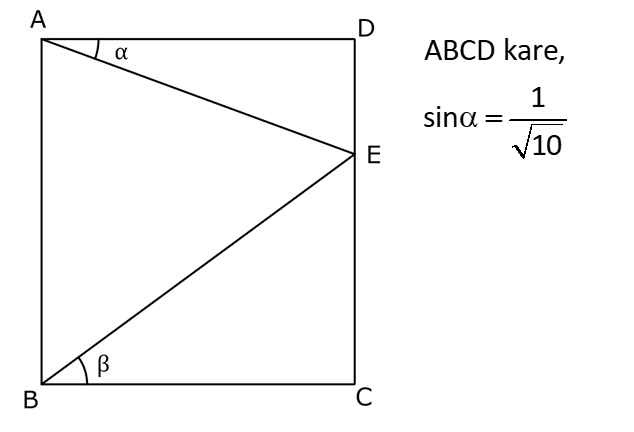
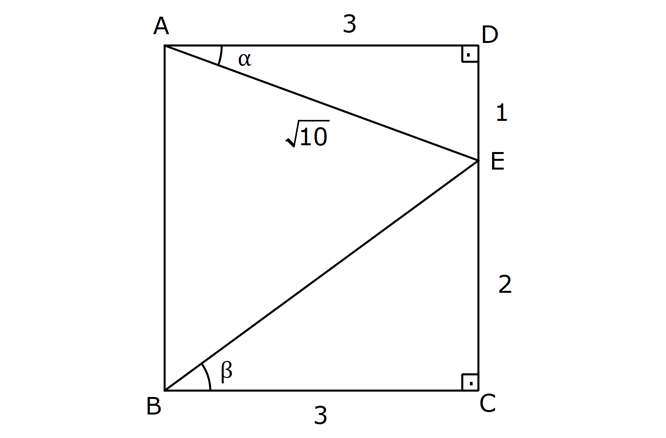
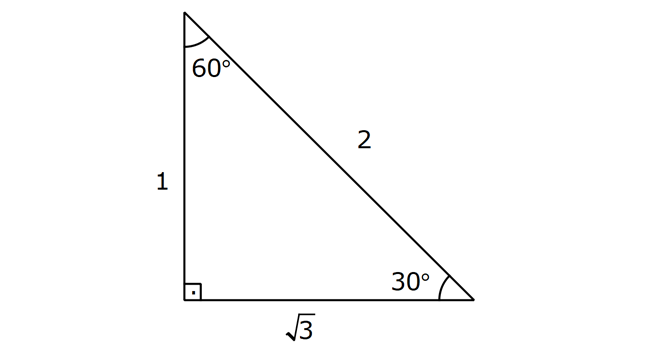
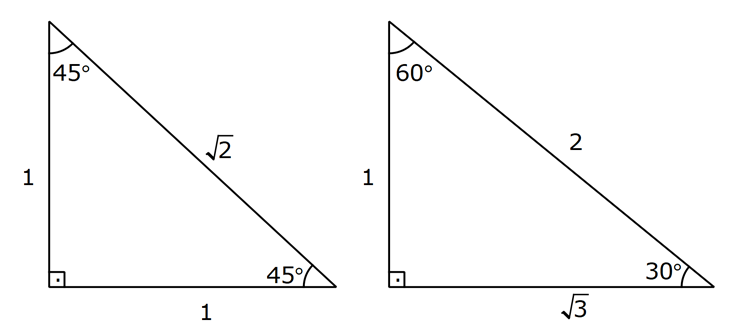
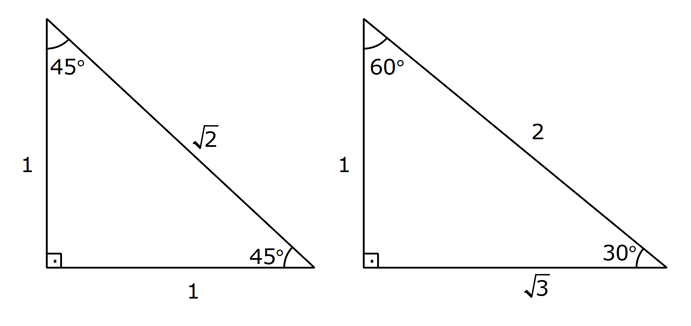
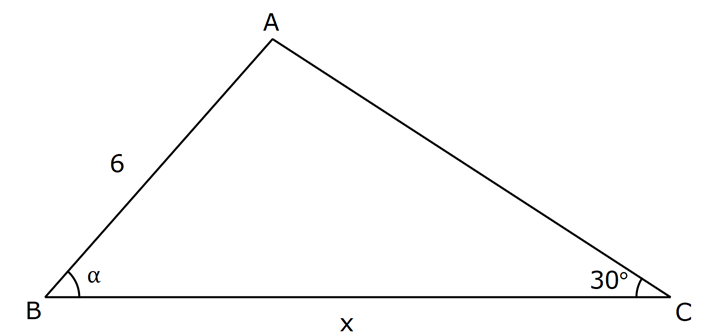
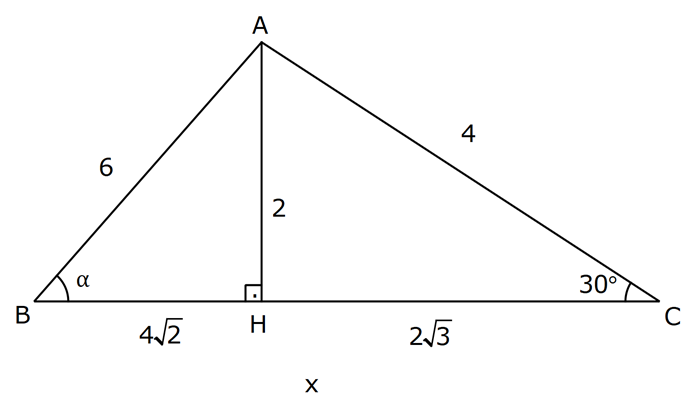
DİK ÜÇGENDE TRİGONOMETRİK ORANLAR www.matematikkolay.net 1) ABC üçgen AC 10 cm AB 6 cm m(BAC) Yukarıda verilenlere göre, sin cos toplamı kaçtır? A) 0,8 B) 1 C) 1,2 D) 1,4 E) 1,5 ÇÖZÜM: 2 ABC üçgeni bir 6 – 8 -10 üçgenidir (3- 4 – 5 in 2 katı). Buna göre, Karşı dik kenar 8 4 sin tir. Hipotenüs 10 5 Komşu dik kenar 6 3 cos = tir. Hipotenüs 10 5 4 3 7 14 Toplarsak 1,4 buluruz. Cevap : D 5 5 5 10 S i Not : Karşı Dik Kenar Komşu Dik K. nüs , Kosinüs Hipotenüs Hipotenüs 2) ABC üçgen AC 41 cm AB 5 cm m(BAC) tan cot Yukarıda verilenlere göre, ifadesi tan .cot kaça eşittir? 17 21 33 37 41 A) B) C) D) E) 10 10 19 20 20 ÇÖZÜM: www.matematikkolay.net 2 2 2 2 4 5 AB uzunluğunu pisagorla bulalım. AB 4 41 AB 16 41 AB 25 AB 5 cm dir. Buna göre, 4 5 5 4 tan cot tan .cot 4 5 5 4 16 25 20 41 dir. Cevap: E 1 20 Karşı Dik K. Komşu Dik K. tan jant , kotan jant Komşu Dik K. Karşı Dik K. Not : 3) ABC üçgen AB 15 cm AC 15 cm BD 4 cm DC 10 cm m(ADC) Yukarıda verilenlere göre, sin kaçtır? 3 185 4 11 185 A) B) C) D) E) 4 11 4 11 185 3 4 ÇÖZÜM: Trigonometrik oranları bulmak için, dik üçgen oluş – turmalıyız. A’dan yükseklik indirelim. ABC üçgeni ikizkenar üçgen olduğu için, taban iki eş parçaya ayrılır 7 ve 7 cm. DH 3 cm olur. AHC üçgeninde pisag 2 2 2 2 2 2 2 or yaparsak, AH 7 15 AH 49 225 AH 176 cm dir. AH 176 11.16 4 11 cm dir. ADH üçgeninde pisagordan AD 3 176 9 176 185 AD 185 cm dir. O halde, 4 11 sin buluruz. Cevap : C 185 4) Yukarıda eş birim karelerin içinde bulunan açılara göre, sin .tan çarpımı kaçtır? 5 5 3 13 5 A) B) C) D) E) 13 3 5 2 3 www.matematikkolay.net ÇÖZÜM: Açıları, rahat hesaplayabileceğimiz dik üçgenler içine taşıyalım. 2 Yukarıda oluşan dik üçgene göre, sin = tür. 13 5 Yukarıda oluşan dik üçgene göre, tan dir. 2 O halde, 2 sin .tan 5 13 2 5 tür. Cevap: A 13 5) ABCD kare, 1 sin 10 Yukarıda verilenlere göre, cot kaçtır? 1 3 2 A) B) C) D) 3 E) 3 3 2 3 ÇÖZÜM: 2 2 2 DE 1 sin DE 1 br, AE 10 br diye – AE 10 biliriz. ADE üçgeninde pisagor yaparsak, AD 1 10 AD 9 AD 3 br olur. Karenin bir kenarı 3 br oldu. O halde, EC 3 1 2 br olur. BCE üçgeninden yararlanarak, B cot C 3 buluruz. Cevap : B EC 2 6) tan30 cot60 ifadesinin değeri kaçtır? sin60 cos30 1 2 3 5 2 A) B) C) D) E) 3 3 2 2 5 ÇÖZÜM: www.matematikkolay.net Yukarıdaki gibi bir 30 – 60 – 90 üçgeni çizip, trigonomet – rik oranları hesaplayabiliriz. (30 nin karşısı 1 birim ise, 60 nin karşısı bunun 3 katı, hipotenüs ise 2 katı dır.) Buna göre, 1 tan30 3 1 cot60 3 sin 3 60 2 3 cos30 dir. Buna göre, 2 1 1 2 3 3 3 2 1 2 tür. Cevap : B 3 3 3 3 3 3 2 2 sin cos tan cot 1 3 3 30 3 2 2 3 3 1 3 60 3 2 2 3 NOT : 30° ve 60° nin trigonometrik oranları 7) (sin45 tan45 ).tan60 ifadesinin değeri kaçtır? 2 3 6 3 6 3 A) B) C) 2 2 2 6 2 3 3 1 D) E) 2 2 ÇÖZÜM: 45 45 90 üçgeninde kenarlar 1-1- 2 şeklinde, 30 – 60 – 90 üçgeninde ise 1- 3 -2 şeklindedir. 1 Buna göre, sin45 2 1 tan45 1 dir. 1 3 tan60 3 tür. O halde, 1 1 (sin45 tan45 ).tan60 1 . 3 2 1 2 3 6 3 2 2 2 6 2 3 dir. 2 Cevap : D sin cos tan cot 2 2 45 1 1 2 2 NOT : 45° nin trigonometrik oranları 8) 2 Dar açılı bir ABC üçgeninde tanA 3, sinB 2 olduğuna göre, C açısı kaç derecedir? A) 15 B) 30 C) 45 D) 60 E) 75 ÇÖZÜM: www.matematikkolay.net tan jantı 3 olan açı 60 dir. A 60 2 sinüsü olan açı 45 dir. B 45 2 O halde, C 180 60 45 180 105 75 dir. Cevap: E 9) ABC üçgen, AB 6 cm, m(ACB) 30 , m(ABC) ve 1 sin olduğuna göre, BC x kaç cm dir? 3 A) 2 2 3 3 B) 6 2 2 3 C) 4 2 2 3 D) 6 2 3 E) 2 2 4 3 ÇÖZÜM: A’dan yükseklik indirelim. AH 1 sin 6 3 AH 6 2 2 2 2 2 2 AH 2 cm dir. ABH üçgeninde pisagordan, 2 BH 6 4 BH 36 BH 32 BH 4 2 cm dir. 3 tan30 olduğundan, 3 2 3 2 AHC üçgeninde tan30 HC 3 HC 3 . HC 2. 3 3 HC 2 3 cm dir. Buna göre, x 4 2 2 3 cm dir. Cevap : C 10) 0 x 90 olmak üzere, 3 sinx ise cotx kaçtır? 7 5 7 3 3 7 2 2 10 A) B) C) D) E) 3 3 5 3 3 ÇÖZÜM: www.matematikkolay.net 2 2 2 2 2 Yukarıdaki gibi bir dik üçgen çizelim. Karşı dik kenar 3 sinx olacak şekilde uzunluk – Hipotenüs 7 ları verelim. Diğer dik kenarı pisagorla hesaplayalım. 3 a 7 a 49 9 a 40 a 40 2 10 br dir. O halde, co Komşu dik kenar 2 10 tx tür. Cevap : E Karşı dik kenar 3


Güzel sorular emeğinize sağlık.