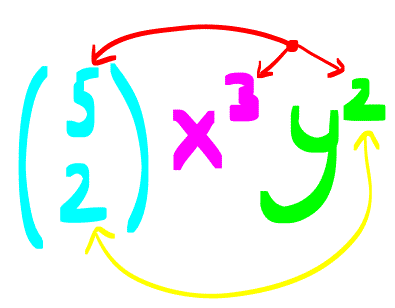 Bu bölümde Binom ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Binom ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…












Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
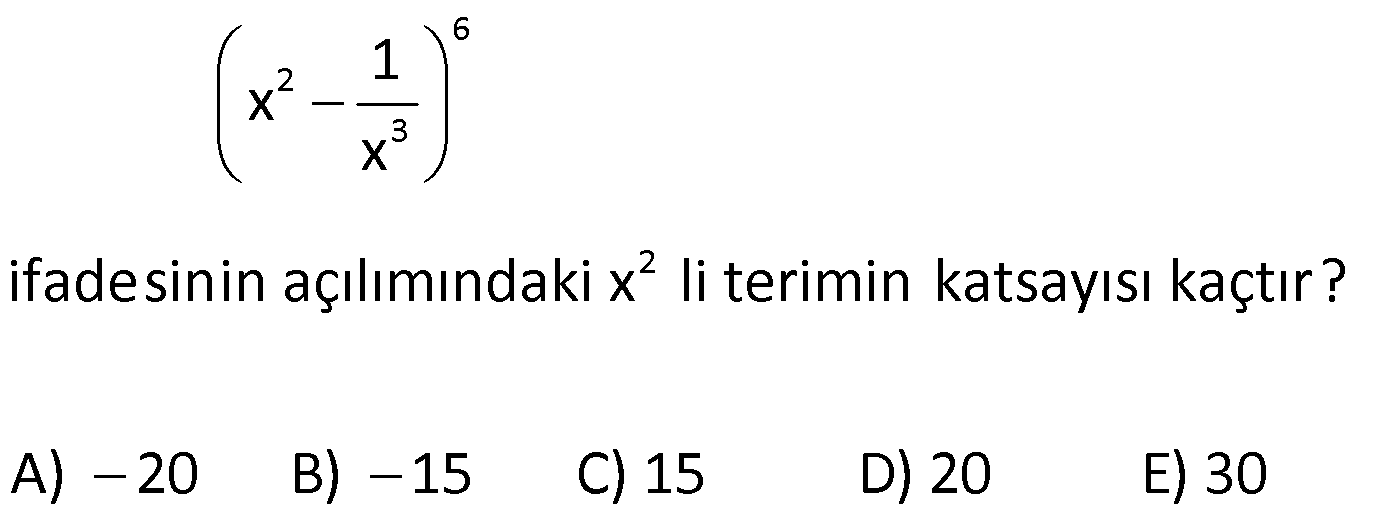
BİNOM www.matematikkolay.net 1) 5 x 3 ifadesi veriliyor. I. Terim sayısı 5 tir. II. Katsayılar toplamı 32 dir. III. Sabit terimi 243 tür. Yukarıdaki öncüllerden hangileri doğrudur ? A) Yalnız I B) I ve III C) Yalnız III D) I ve II E) II ve III ÇÖZÜM: n 5 I (x y) ifadesinin açılımında n 1 tane terim vardır. Katsayılar toplamını bulmak için x y 1 verilir (x 3) ifadesinde n 5 tir. Terim sayısı n 1 5 1 . Sabit terimi bulmak için x y 0 veri i 6 dı l r. r. 5 5 5 5 . öncül yanlış. x 1 yazarsak 1 3 2 32 bulunur. II. öncül yanlış. x 0 yazarsak (0 3) 3 243 bulunur. III. öncül doğru. Cevap : C 2) n 2x y ifadesinin açılımında 6 tane terim olduğuna göre, bu terimlerin katsayılar toplamı kaçtır? A) 9 B) 27 C) 81 D) 243 E) 729 ÇÖZÜM: n 5 5 2x y ifadesinin terim sayısı n 1 6 n 5 tir. Katsayılar toplamı için x y 1 yazalım. 2 1 1 3 243 bulunur. Cevap : D 3) n 3x ay 2 ifadesinin sabit terimi 32, katsayılar toplamı 243 olduğuna göre, a n toplamı kaçtır? A) 2 B) 1 C) 3 D) 5 E) 7 ÇÖZÜM: n n n n n 5 (x y z) ifadesinin açılımında Katsayılar toplamını bulmak için x y z 1 verilir. Sabit terimi bulmak iç 3x ay 2 ifadesinin sabit terimi 32 3 0 a 0 2 32 2 32 in x y z 0 ver 2 2 n 5 tir. ilir. 3 5 5 5 5 5 5 x ay 2 ifadesinin katsayılar toplamı 243 3 1 a 1 2 243 1 a 3 1 a 3 1 a 3 a 2 dir. a n 2 5 3 bulunur. Cevap : C 4) 6 (2x y) ifadesinin x in azalan kuvvetlerine göre açılımındaki baş tan 3.terimin katsayısı kaçtır? A) 240 B) 160 C) 30 D) 160 E) 240 ÇÖZÜM: 6 4 2 2 4 4 4 n r) r 2 (n (x y) ifadesinin x in azalan kuvvetlerine göre n açılımındaki r 1 . m terim: x ü g y di 2x y n 6 dır. r 1 3 r 2 dir. Şi di formül uy ulayalım. 6 6 5 2x y 2 x y 2 2 15 16 x r r y . 4 2 katsayı 240 x y 240 bulunur. Cevap : E 5) BİNOM www.matematikkolay.net 4 2 5 2 2 5 1 2x x ifadesinin açılımındaki ortadaki terimi bulunuz. A) 32x B) 24x C) 24 D) 24x E) 32x ÇÖZÜM: 4 2 2 2 2 4 4 2 2 2 n O 2 rtadaki terim 1 i bulmak için r alınır. 6 x 1 2x n 4 r 2 dir. x 4 1 x 4x 24x 2 x 24x bulunur. 2 Cevap : B 6) 6 4 2 2 4 3 3 5 x 2y ifadesinin x in azalan kuvvetlerine göre açılımındaki sondan 3. terimi aşağıdakilerden hangisidir? A) 60x y B) 240x y C) 160x y D) 6x y E) 5 96xy ÇÖZÜM: 6 6 x 2y ifadesinin x in azalan kuvvetlerine göre açılımındaki sondan 3. terimi bulmak için pratik olarak x li ve y li terimin yerini değiştirip, baş tan 3. yü hesaplar gibi çözebiliriz. 2y x için çözel 6 2 2 im. n 6, r 1 3 r 2 6 6 2y x 2 3 5 2 4 2 4 2 2 4 6 2y x 15.16y x 240x y bulunur. x 2y ifadesinin açılımında n 1 terim vardır. n 6 6 1 7 terim vardır. Sondan 3. terimin baş tan kaçıncı terim olduğunu düşün II.Yol: 4 6 4 6 e eşit 2 2 4 2 4 elim.7 den 3 birim geriye sararsak 5. terime geliriz. r 1 5 r 4 tür. 6 x 2y 4 6 5 x 16y 240x y bulunur. 2 Cevap : B 7) n 2 3 (3x 2y) ifadesinin açılımındaki terimlerden biri A.x y A olduğuna göre değeri kaçtır? n A) 144 B) 72 C) 36 D) 72 E) 144 ÇÖZÜM: n 2 3 2 3 2 3 5 lisine eşittir. 2 2 3 2 3 (3x 2y) ifadesinin açılımındaki terimlerden biri A.x y ise n 2 3 5 ve r 3 tür. 5 3x 2y 10 9x 8y 3 720x y A x y A 720 A 720 144 bulunur. n 5 Cevap : A BİNOM www.matematikkolay.net 8) 7 3 2 m 8 2x y ifadesinin açılımındaki terimlerden biri A.x .y oldu- ğuna göre, A m değeri aşağıdakilerden hangisidir? A) 271 B) 131 C) 149 D) 289 E) 309 ÇÖZÜM: 7 3 2 m 8 2 8 r 2 8 2r 8 2x y ifadesinin açılımındaki terimlerden biri A x y verilmiş. n 7 dir. r yi bulmaya çalışalım. y nin kaçıncı kuvveti alınmıştır ki açılımda y gelmiş. y y y y 2r 8 r 4 tür. 7 4 7 4 4 3 2 m 8 7 ne eşit 3 2x y A x y 7 6 5 321 9 8 m 8 9 8 m 8 8x y A x y 280x y A x y A 280 ve m 9 dur. A m 280 9 289 dur. Cevap : D 9) 6 2 3 2 1 x x ifadesinin açılımındaki x li terimin katsayısı kaçtır? A) 20 B) 15 C) 15 D) 20 E) 30 ÇÖZÜM: 6 2 3 2 r 6 r 2 2 3 3r 12 2r 2 1 x x ifadesinin açılımındaki x li terimin katsayısını bulmak için fomülü kullanalım. n 6 verilmiş. 6 1 x A x diyelim. r x 6 x x A.x r 6 r 3r 3r 12 2r 2 3r 12 2r 3r 2 12 5r 2 6 2 2 2 3 8 6 8 x 1 x A.x 6 1 x A x r x x 12 5r 2 r 2 dir. Şimdi r değerini yerine yazıp katsayıyı bulalım. 6 6 5 x x x x 2 2 15x 6 2 6 2 2 3 3 15x A 15 bulunur. 1 1 x burada 6 yı x ve e nasıl dağıtabilex x ceğimizi tahmin etmeye çalışalım. Sonucun çift kuvvetli olmasından dolayı 6 yı çift iki sayıya parçalam II. Yol Tahmin Yolu 2 8 4 2 8 2 3 6 6 amız lazım. Sonuçta da pozitif kuvvet kaldığına göre birinci terimin daha büyük kuvvetini alacağız. 4 e 2 diye düşünürsek; 1 1 x x x x olur. x x x Demek ki r 2 dir. Devamı ilk yolla aynı şeki lde çözülür. Cevap : C 10) 9 2 1 2x x ifadesinin açılımındaki sabit terim kaçtır? A) 42 B) 84 C) 168 D) 336 E) 672 ÇÖZÜM: BİNOM www.matematikkolay.net 9 2 0 r 9 r 2 0 18 2r 0 r 18 2r r 0 18 3r 1 2x x ifadesinin açılımında sabit terim x lı terimdir. r yi bulmak için formülün sadece üslerle ilgili kısmını kullanabiliriz. 1 1 x x x x x x x x x 3 0 9 ‘ e eşit 3 6 9 6 2 0 x 18 3r 0 18 3r r 6 dır. 9 1 2x . A x 6 x 9 3 8 4 7 3 2 6 8 x 1 6 1 x 84 8 672 bulunur. Cevap : E 11) 15 14 12 10 7 15 15 15 15 … 0 2 4 14 ifadesinin eşiti aşağıdakilerden hangisidir? A) 2 B) 2 C) 2 D) 2 E) 2 ÇÖZÜM: 14 14 14 14 14 14 14 yazabiliriz. 0 1 2 3 4 13 14 1 Hatırlatma: n n 1) 1 0 n n n 2) n 1 n 1 n n n 1 3) r r 1 r 15 15 15 15 … 0 2 4 14 14 0 1 n 14 4 14 14 14 14 14 … 1 2 3 4 13 14 Bu açılım 14 elemanlı bir kümenin tüm alt kümelerinin toplamının açılımıdır. Alt küme sayısı 2 2 bulunur. Cevap : B 12) 8 7 6 16 15 12 9 8 8 8 8 8 10 10 10 … 0 1 2 8 işleminin sonucu kaçtır? A) 3 B) 3 C) 3 D) 3 E) 3 ÇÖZÜM: n n n 1 n 2 2 n n n 2 8 n 7 1 6 8 n 0 n n n n x y x x .y x .y … y 0 1 2 n n n n n (x 1) x x x 8 8 8 8 .10 10 10 … 0 1 2 . 8 8 8 .10 1 . . dir. 0 1 2 n 0 1 1 8 7 8 8 8 2 16 8 .10 1 … . 1 8 10 1 9 3 3 bulunur. Cevap : A
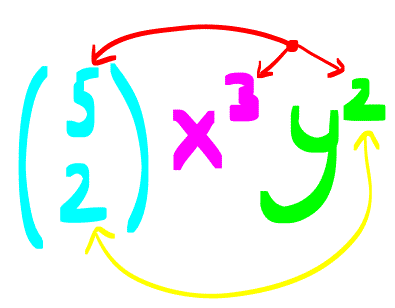 Bu bölümde Binom ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Binom ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…


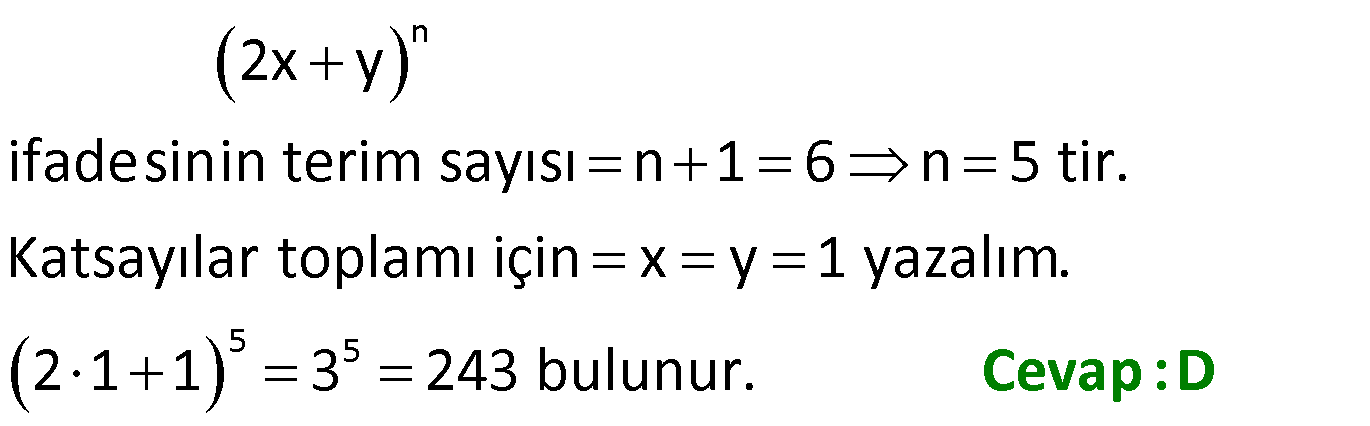
















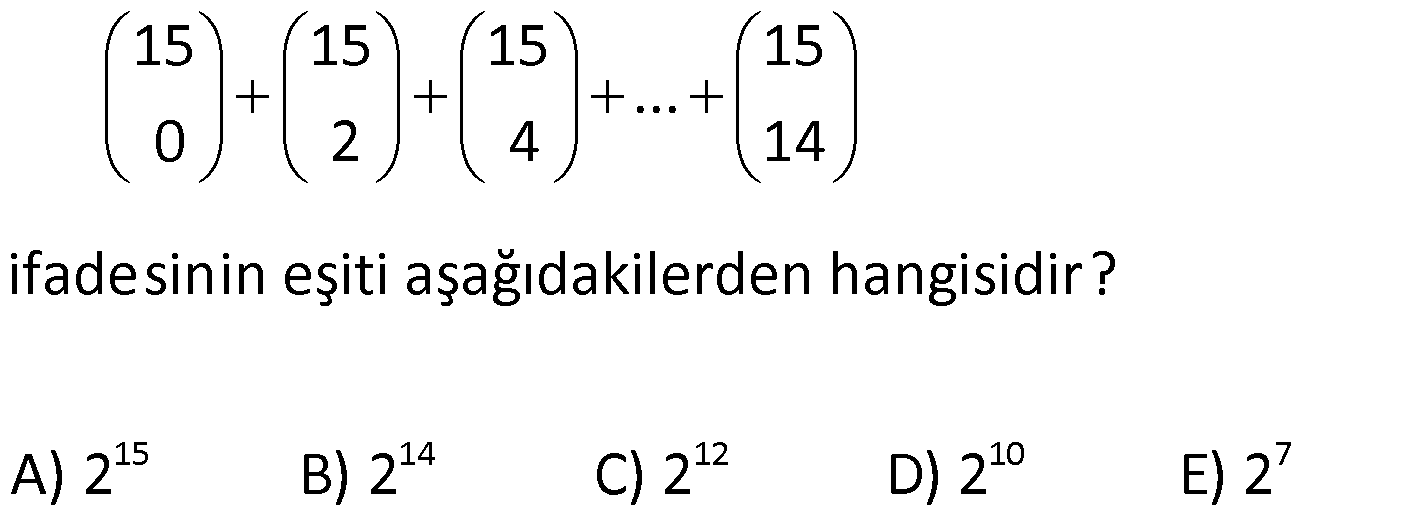

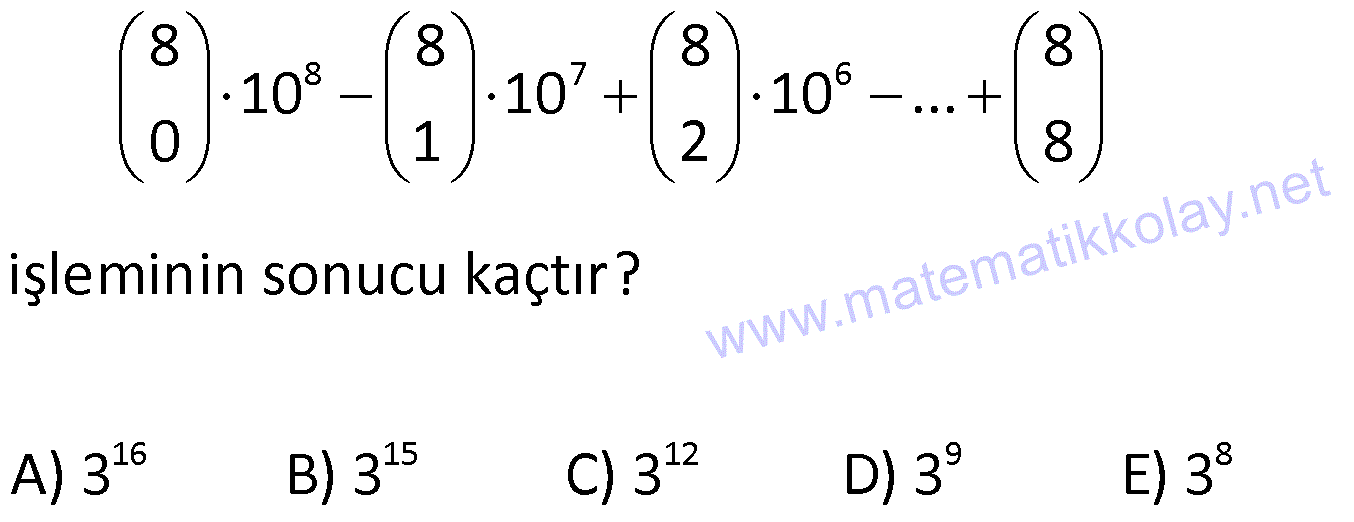





oldukça güzel..matematikçi olarak öğrencilere tavsiye ettim.
çok kolaydı sorular az ama yinede güzel
çok faydalıydı teşekkürler