Bu bölümde Açılarına Göre Özel Üçgenler ile ilgili 7 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
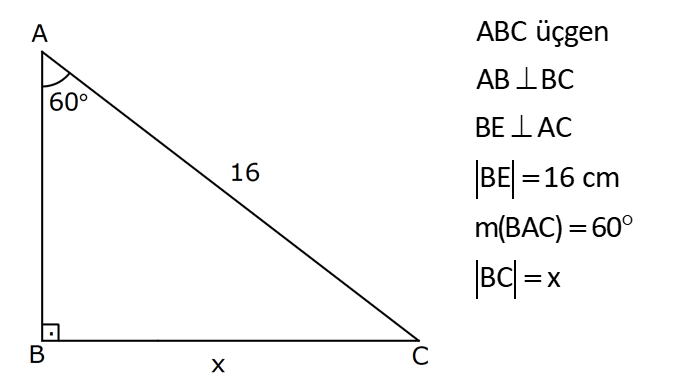
1.SORU
 |  |  |  |  |
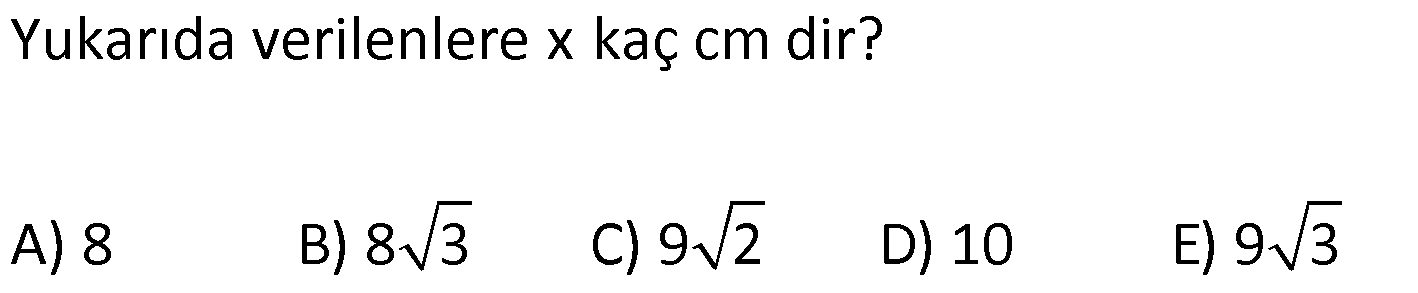
Çözüm için Tıklayınız.
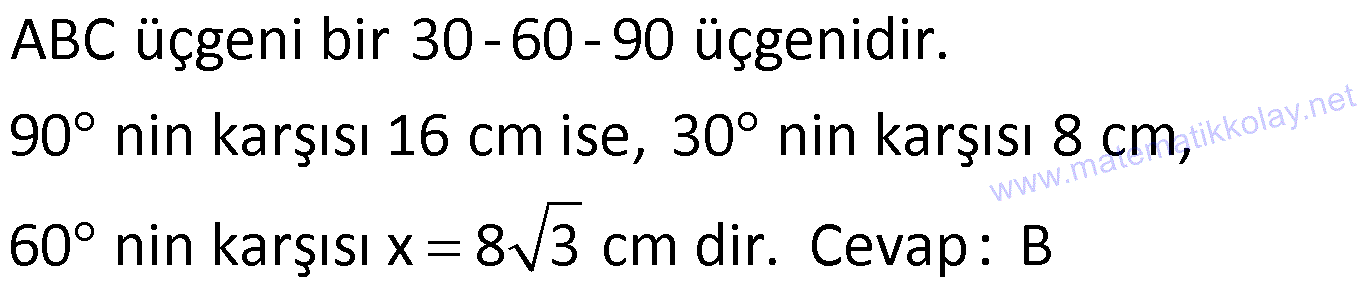
2.SORU
| | | | | |
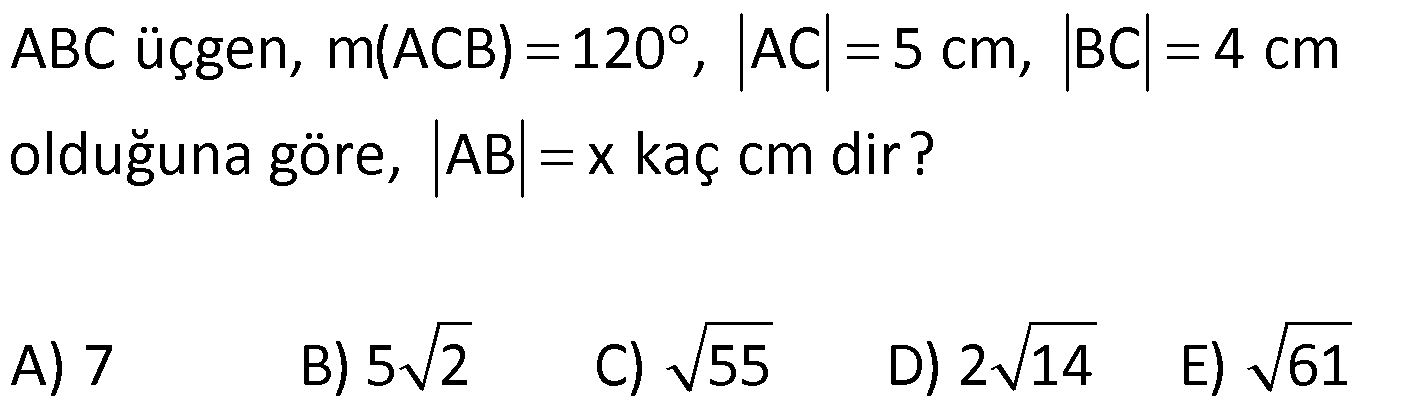
Çözüm için Tıklayınız.
3.SORU
| | | | | |
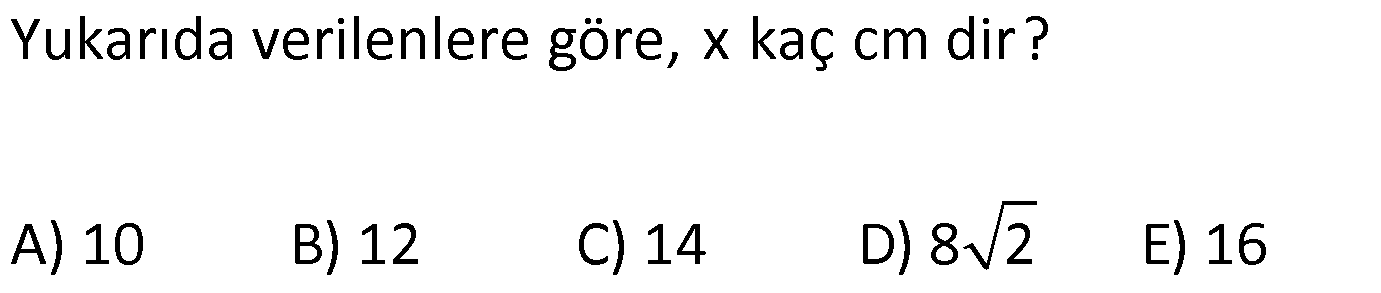
Çözüm için Tıklayınız.
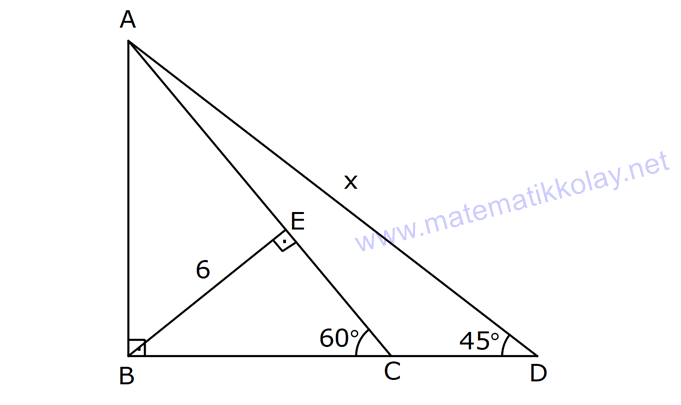
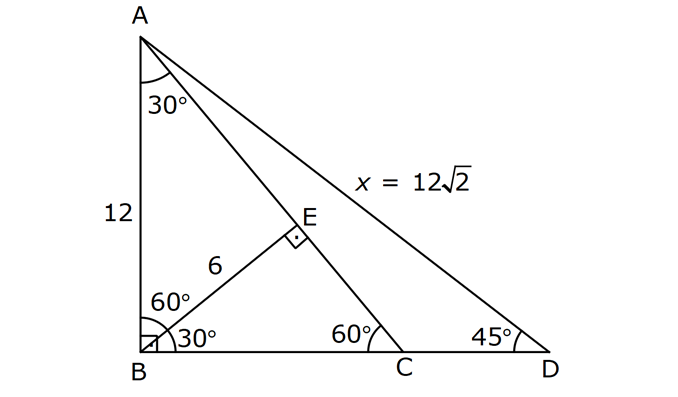
4.SORU
| | | | | |
Çözüm için Tıklayınız.
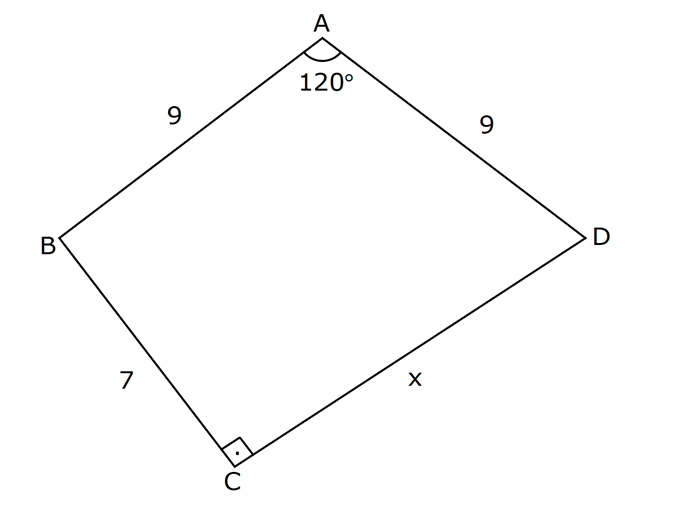
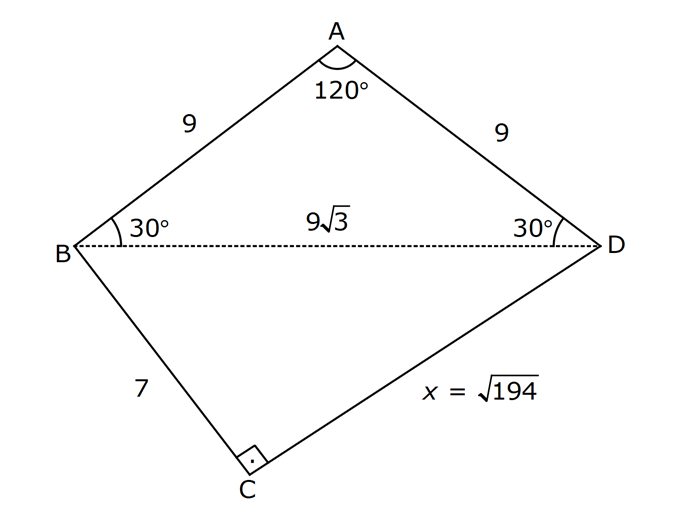
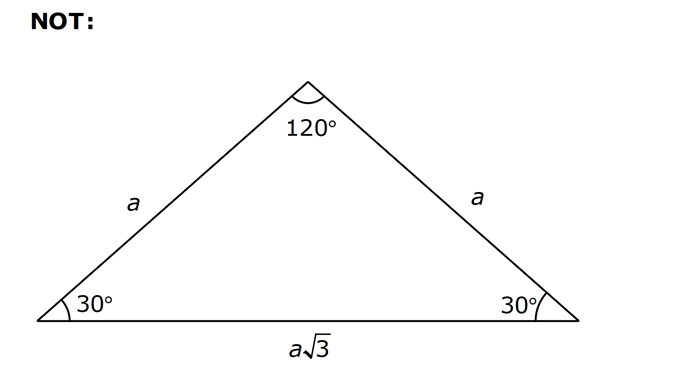
5.SORU
| | | | | |
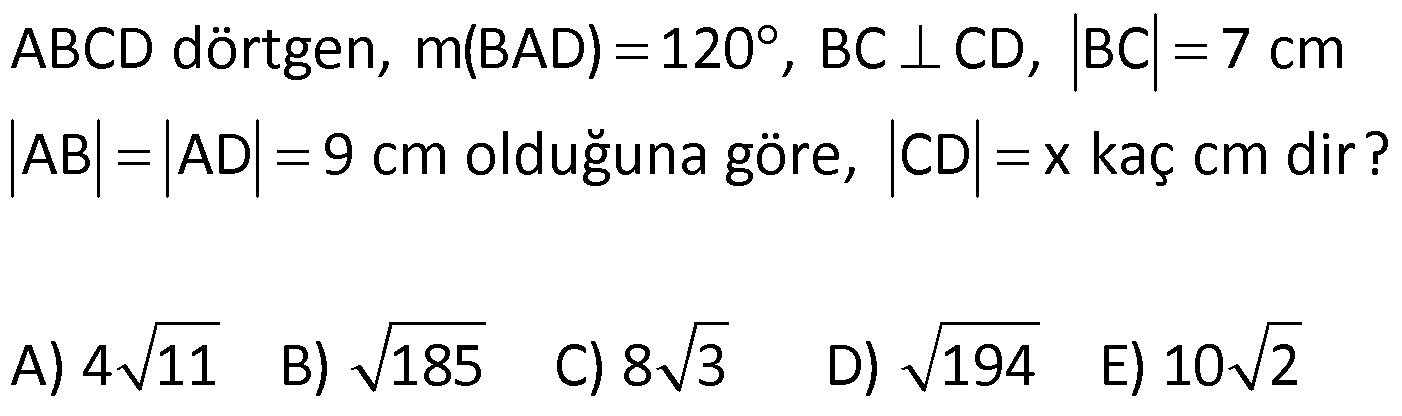
Çözüm için Tıklayınız.
6.SORU
| | | | | |
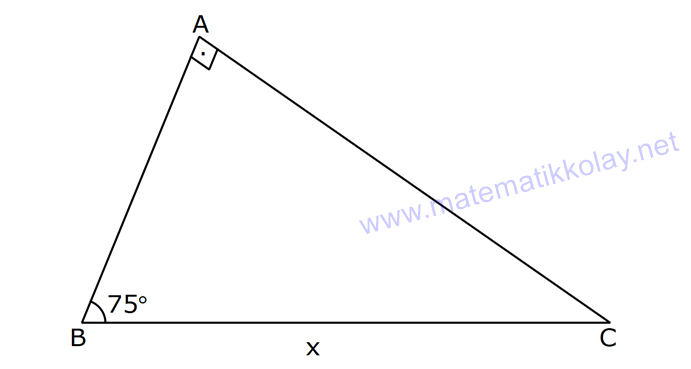
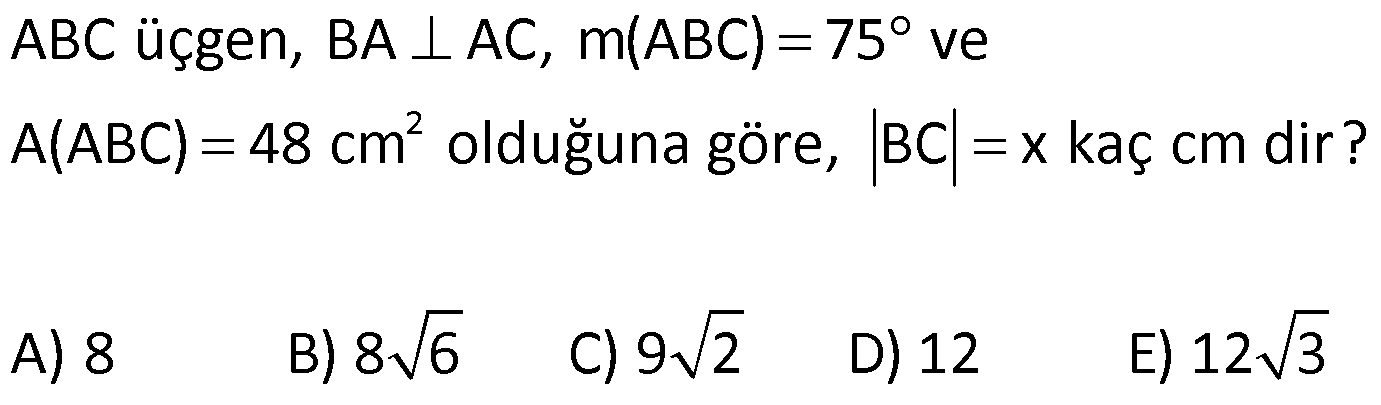
Çözüm için Tıklayınız.
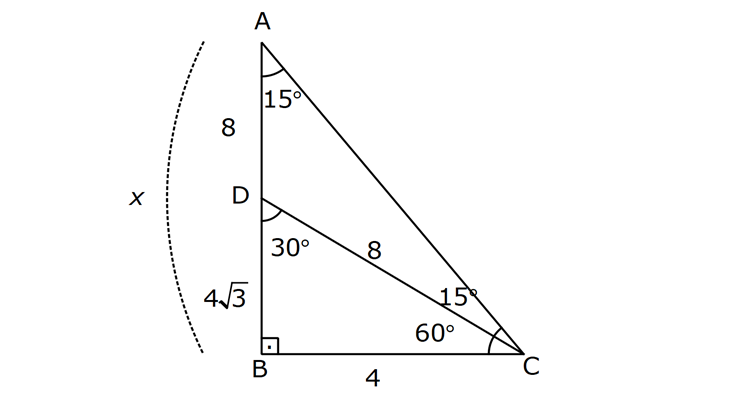
7.SORU
| | | | | |
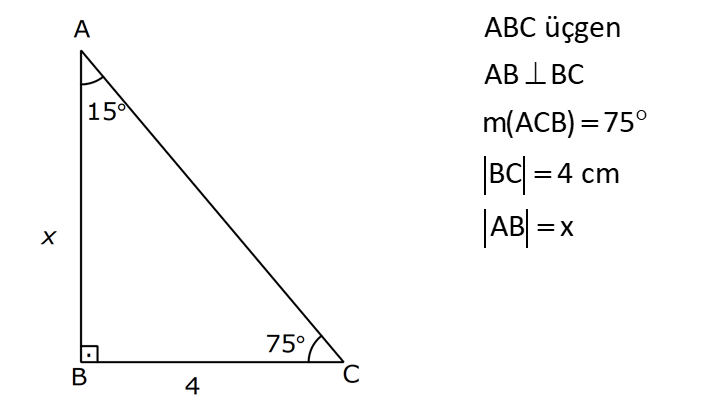
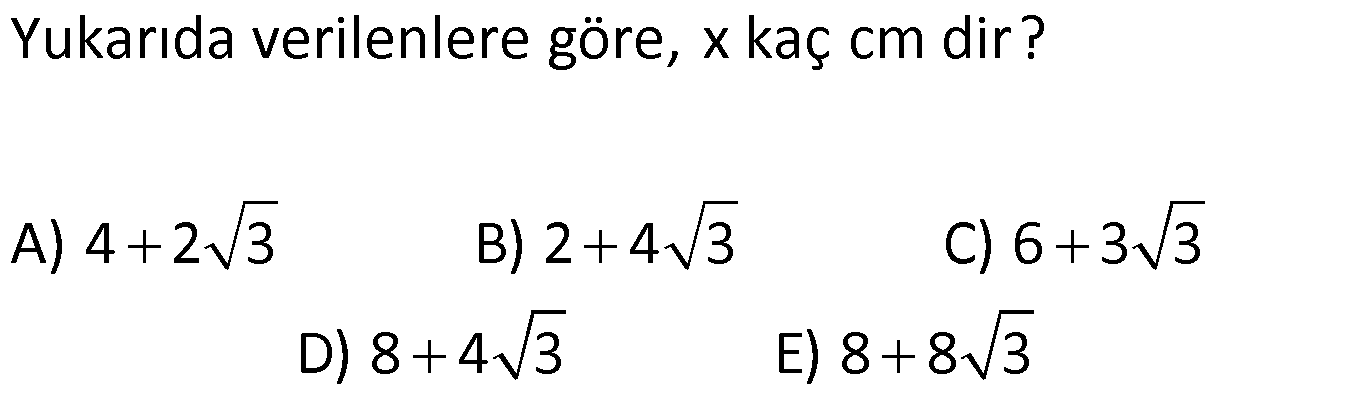
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
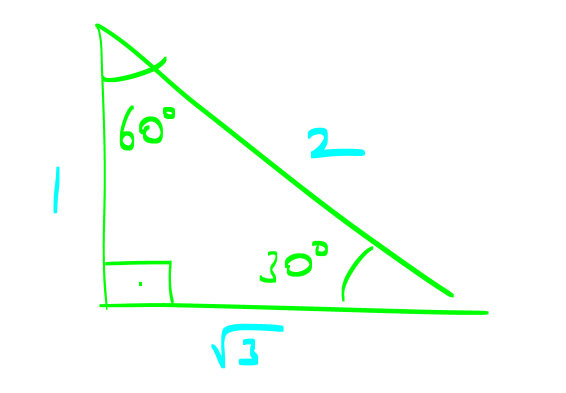
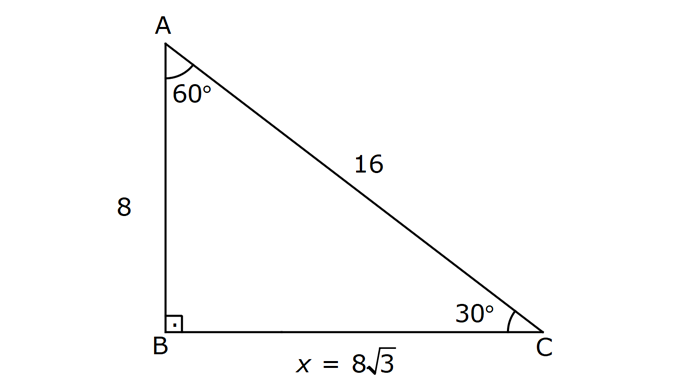
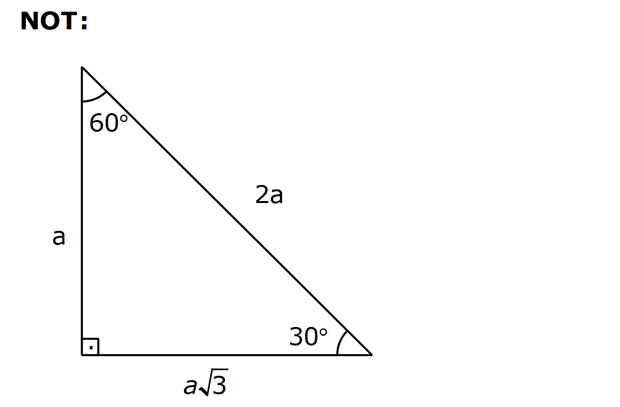
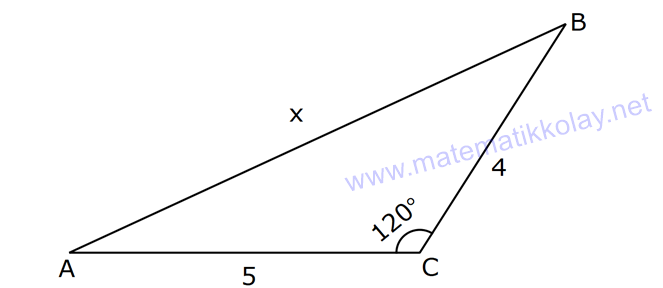
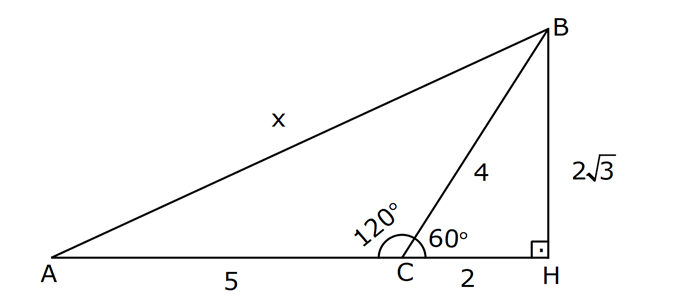
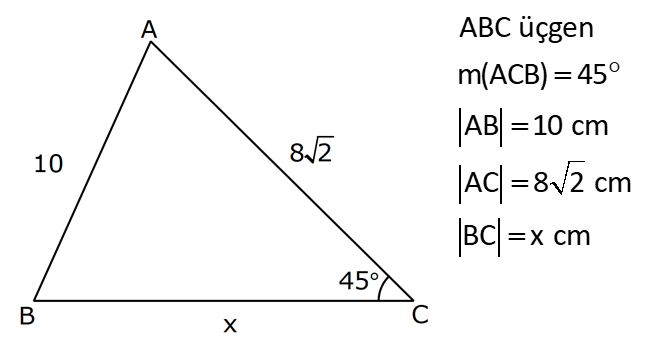
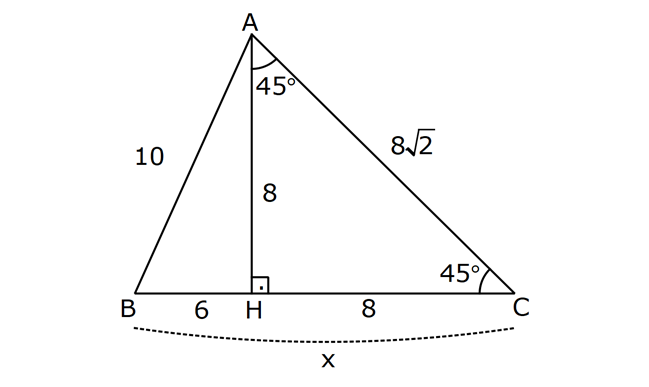
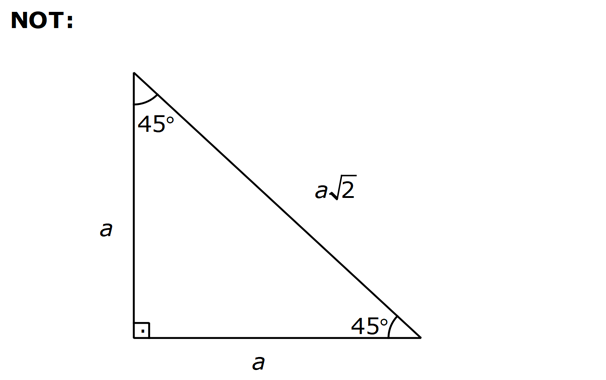
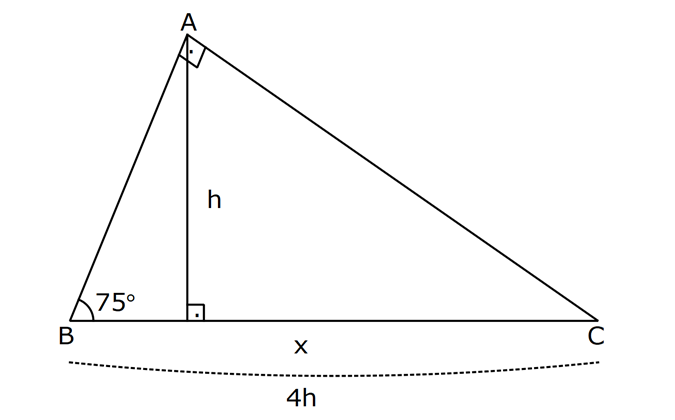
AÇILARINA GÖRE ÖZEL ÜÇGENLER www.matematikkolay.net 1) ABC üçgen AB BC BE AC BE 16 cm m(BAC) 60 BC x Yukarıda verilenlere x kaç cm dir? A) 8 B) 8 3 C) 9 2 D) 10 E) 9 3 ÇÖZÜM: ABC üçgeni bir 30 – 60 – 90 üçgenidir. 90 nin karşısı 16 cm ise, 30 nin karşısı 8 cm, 60 nin karşısı x 8 3 cm dir. Cevap: B 30 60 90 üçgeninde, Hipotenüs, 30 nin karşısındaki kenarın 2 katı ; 60 nin karşısındaki kenar ise, 30 nin karşısındaki kenarın 3 katıdır. 2) ABC üçgen, m(ACB) 120 , AC 5 cm, BC 4 cm olduğuna göre, AB x kaç cm dir? A) 7 B) 5 2 C) 55 D) 2 14 E) 61 ÇÖZÜM: 2 2 2 2 B’den yükseklik indirelim ve AC doğrusunu uzatalım. BCH üçgeni bir 30 – 60 – 90 üçgeni olur. Hipotenüs 4 cm ise, 30 nin karşısı 2, 60 nin karşısı 2 3 cm olur. AHB üçgeninde pisagor yaparsak, x 7 2 3 x 49 12 2 x 61 x 61 cm dir. Cevap : E www.matematikkolay.net 3) ABC üçgen m(ACB) 45 AB 10 cm AC 8 2 cm BC x cm Yukarıda verilenlere göre, x kaç cm dir? A) 10 B) 12 C) 14 D) 8 2 E) 16 ÇÖZÜM: 2 2 2 2 2 A’dan yükseklik indirelim. AHC üçgeni 45- 45- 90 8 2 üçgeni olur. AH HC 8 cm olur. 2 ABH üçgeninde pisagor yaparsak, 10 BH 8 100 BH 64 36 BH BH 6 cm olur. x 6 8 14 cm buluruz. Cevap : C 45 45 90 üçgeninde, Hipotenüs, 45 nin karşısındaki kenarın 2 katıdır. 4) ABD üçgen, AB BD, BE AC, BE 6 cm, m(BCA) 60 , m(BDA) 45 olduğuna göre, AD x kaç cm dir? A) 8 B) 12 C) 12 2 D) 8 3 E) 9 6 ÇÖZÜM: 30 nin karşısı Hipotenüs 45 nin karşısı 45 nin karşısı ABE üçgeni bir 30 – 60 – 90 üçgenidir. BE 6 cm ise, AB 12 cm dir. ABD üçgeni de bir 45- 45- 90 üçgenidir. AB 12 cm ise, x 12 2 cm dir. Cevap : C www.matematikkolay.net 5) ABCD dörtgen, m(BAD) 120 , BC CD, BC 7 cm AB AD 9 cm olduğuna göre, CD x kaç cm dir? A) 4 11 B) 185 C) 8 3 D) 194 E) 10 2 ÇÖZÜM: 2 2 2 2 2 BD’yi çizelim. ABD üçgeni bir 30 – 30 -120 üçgeni olur. BD 9 3 cm dir. (30 nin karşısının 3 katı) BCD üçgeninde pisagor yaparsak, x 7 9 3 x 49 243 x 194 x 194 cm olur. Cevap : D 30 30 120 üçgeninde, Hipotenüs, 30 nin karşısındaki kenarın 3 katıdır. 6) 2 ABC üçgen, BA AC, m(ABC) 75 ve A(ABC) 48 cm olduğuna göre, BC x kaç cm dir ? A) 8 B) 8 6 C) 9 2 D) 12 E) 12 3 ÇÖZÜM: www.matematikkolay.net 2 2 15- 75- 90 üçgeninde, hipotenüs, yüksekliğin 4 katıdır. h.4h Buna göre, A(ABC) 2 48 2h 24 h h 2 6 cm dir. x Not : 4h 4.2 6 8 6 cm dir. Cevap: B 7) ABC üçgen AB BC m(ACB) 75 BC 4 cm AB x Yukarıda verilenlere göre, x kaç cm dir? A) 4 2 3 B) 2 4 3 C) 6 3 3 D) 8 4 3 E) 8 8 3 ÇÖZÜM: 30 nin karşısı 60 nin karşısı 90 nin karşısı Yukarıdaki gibi, 75 ‘yi 60 ve 15 olacak şekilde bölelim. DBC üçgeni 30 – 60 – 90 üçgeni olur. BC 4 cm ise, DB 4 3 ve DC 8 cm olur. ADC üçgen inin iki iç açısı 15 dir. Dolayısıyla, AD DC 8 cm olur. Buna göre, x 8 4 3 cm dir. Cevap: D
Soruları çözebildim gerçekten güzel soruları teşekkürler:))
çog iyi